相似形中的“凹槽圖形”

羅智國

相似形中的“凹槽圖形”

羅智國

我們在八年級學習全等時，經常會碰到這樣的問題：

如圖1：直線l過正方形ABCD的頂點B，點A、C到直線l的距離分別是1和2，則EF的長是.

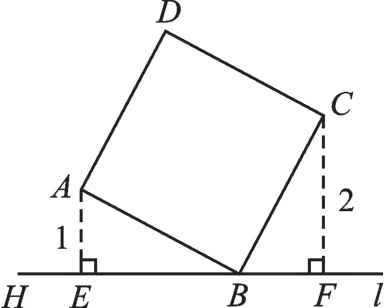
圖1

在這個圖形中，因為AE⊥BE，CF⊥BF，得∠AEB=∠BFC=90°，所以∠EAB+∠ABE=90°，∠ABE+∠FBC=90°，得∠EAB=∠FBC，再加條件AB=CB得△ABE≌△BCF，從而有BE=CF=2，AE=BF=1，所以EF=BE+BF=3.

在這個圖形中，有∠AEB=∠ABC=∠BFC=90°，我們把存在這樣關系的圖形叫“一線三角”，也俗稱“凹槽圖形”.如果把其中的線段相等條件去掉，則這樣的凹槽圖形必有△ABE∽△BCF，當然，我們也可嘗試把90°換成60°或任意的角，都可以得△ABE與△BCF相似.今后同學們在做選擇、填空題時碰到這類的凹槽圖形可直接加以運用，以加快解題的速度，也可以讓我們在解題時很快找到思路.

“凹槽圖形”在中考中也是層出不窮，特別在相似中運用廣泛.

如圖2，在四邊形ABCD中，AB∥CD，∠A=90°，AB=2，AD=5，CD＞AB，P是AD上一動點（不與A，D重合），PE⊥BP，P為垂足，PE交DC于E.請探索點P在運動過程中，四邊形ABED能否構成矩形？如果能，求AP長；如果不能，說明理由.

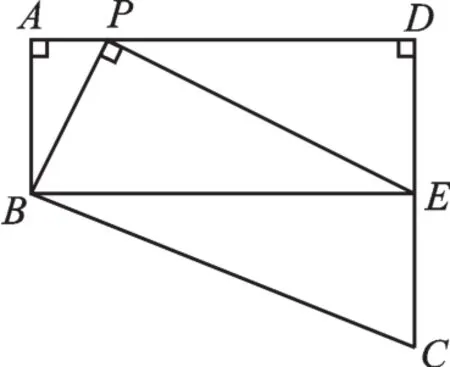
圖2

在解決這道題目時，同學們首先應該在題目中審清條件，快速地找到題目中的形——“凹槽圖形”，利用△ABP∽△DPE，得，我們可設AP=x，則，求得.如果四邊形ABED為矩形，則有，解得x=1或x=4，驗證知：當AP=1或AP=4時，四邊形ABED構成矩形.

審題很關鍵，通過審清題目，配合圖形找出圖形中蘊含的特殊圖形，然后設未知數通過相似建立等量關系解決問題.同學們在今后解題時可以借鑒.但并不是每一條題目中的“凹槽”都是一目了然的，有些題目我們必須自己增加輔助線構建“凹槽圖形”.

如圖3，在△ABC中，AG⊥BC于點G，分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF，射線GA交EF于點H.若AB=kAE，AC=kAF，試探究HE與HF之間的數量關系，并說明理由.

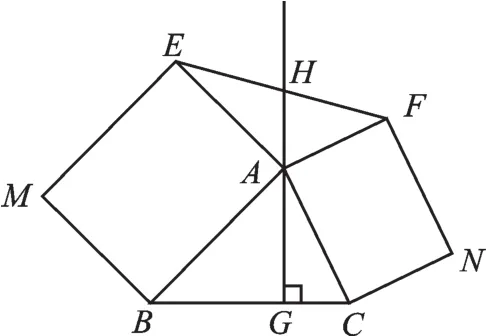
圖3

這道題目有一定的難度，可能許多同學一時半刻沒有思路去解決.這時建議同學們再去好好審題，找到圖形中的隱藏的量，很快就可以發現：只需分別從E，F向HG引垂線，作EP⊥HG，FQ⊥HG，垂足分別為P，Q，如圖4，這樣就出現了我們要的“凹槽圖形”，而且有兩個，則△ABG∽△EAP，△ACG∽△FAQ，得出兩個比例等式所以，由此得EP=FQ.這時可以利用△EPH≌△FQH得HE=HF.

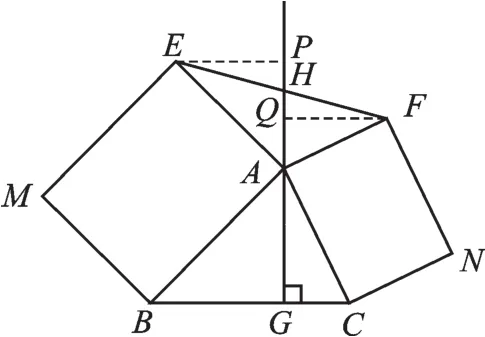
圖4

將復雜問題簡單化，是我們成功解題的關鍵.這就要求我們在平時的學習中要注意解題后的反思、小結，積累解題的經驗，形成自己特有的解題方法與技巧，以不變應萬變.

學習中解決數學問題，都是由淺入深，由易到難的.同學們只要抓住題目的根本條件，把最原始的基本圖形保持在腦海中，如我們上面講的相似中的“凹槽圖形”，這樣才能快速找到解決問題的途徑，進而解別人所不能解的題目，并提升自己學習數學的思維與方法.

（作者單位：江蘇省興化市張郭中心校）