特殊值法
——高中數學解題的一劑“良方”
■山東省萊蕪一中2015級 劉雨如(指導教師:王玉玲)
特殊值法
——高中數學解題的一劑“良方”
■山東省萊蕪一中2015級 劉雨如(指導教師:王玉玲)
特殊值法作為解題的利器,主要是借助特殊情境的創設或者特殊值的選取來達到豐富解題條件、降低解題難度的目的,尤其是對于某些選擇題或者缺乏解題條件的題目,采用特殊值法可能會取得意想不到的效果。
一、轉換角度,變換思路
涉及角度的數學題目是高中數學的重要組成部分,其涵蓋了證明題、求解題等多種類型。如果可以借助特殊值法的合理應用,適當地對相關角度進行變換,那么可以大大簡化相應題目,降低其解題難度。
例1已知銳角△ABC的三邊分別為a、b和c,三個角度分別為A、B和C,且其中那么可知
解析:這是一道涉及“角邊”的數學題目,且已知三角形為銳角三角形,剩余的已知條件為邊角之間的關系。
一般計算流程:6abcosC=a2+b2,6ab由三角形的邊角關系以及其同三角函數之間的關系知同樣進行適當變化得繼續進行簡化得sinAsinBcosC=
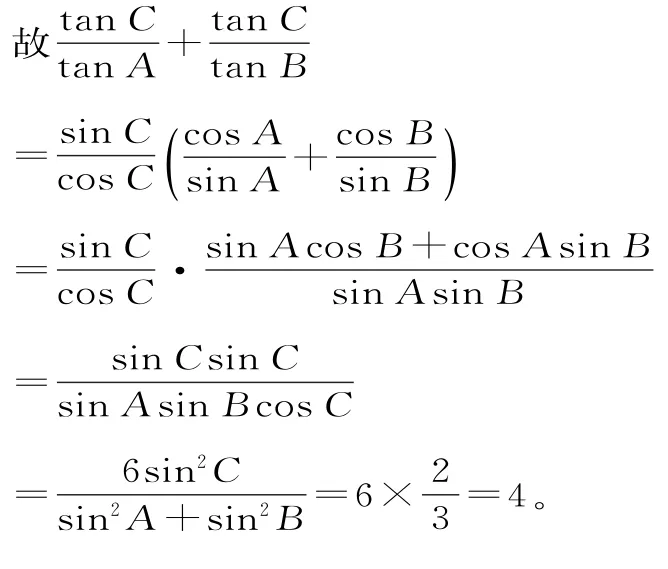
由上述一般計算流程可知:該題的求解難度比較大,實際求解非常費時費力,且很難得到正確答案。而如果采用特殊值法,假設A=B,那么可以將已知條件中的三角形轉換為等腰銳角三角形,從而有助于簡化題目中的已知關系,減少計算出錯概率,達到快速求解的目的。
二、構造函數,優化解題
構造函數法在多種類型的數學題目中均具有很強的應用性,尤其是在不等式方面。
例2已知-2≤a≤2,不等式ax2-2x-a+1<0恒成立,試求x的取值范圍。
解析:將ax2-2x-a+1<0進行適當變換,可知a(x2-1)-2x+1<0,此時可以根據x的取值來進行適當變化,具體可以劃分成三種情況來進行分別討論。①當x=1時,可知-2×1+1=-1<0,原不等式成立;②當x=-1時,可知-2(-1)+1=3>0,原不等式不成立;③當x≠±1時,構造一次函數f(a)=a(x2-1)-2x+1,可知當-2≤a≤2時,f(a)<0恒成立,此時存在f(-2)<0和f(2)<0,可知
本題求解的突破口在于結合相應問題的特征來合理構造一次函數,借助一次函數的性質來進行求解,這樣可以有效地避免分類討論過程中出現的繁雜性,優化解題過程。
三、特殊定位,化難為易
從理論上來講,高中數學知識涉及廣泛的規律和原則,問題處理的方法也比較多。但在實際的問題求解中,多數同學常常傾向于采用最基本、最常見的方法來處理。針對涉及“變化的量”方面的數學問題時,如果繼續采用傳統方法,那么就顯得比較繁雜,此時如果采用特殊值法來定位相應的變量,然后再配合相關數學思想和方法,那么就可以快速地求解了。
(責任編輯 趙 平)

