具有時滯和脈沖接種的SEIR模型

仝耀華，石巖嶺

（1.山西大同大學數學與計算機科學學院，山西大同 037009；2.山西大同大學網絡信息中心，山西大同037009）

具有時滯和脈沖接種的SEIR模型

仝耀華1，石巖嶺2

（1.山西大同大學數學與計算機科學學院，山西大同 037009；2.山西大同大學網絡信息中心，山西大同037009）

建立了一個具有脈沖和時滯的模型來描述一類具有脈沖接種和染病潛伏期的疾病。運用時滯微分方程和脈沖微分方程的理論，得到了系統持久性的充分條件。

時滯；傳染病模型；平衡點；脈沖接種

Kermark和Mckendrick在1927年利用動力學方法建立了三倉室SIR傳染病模型并對其傳播規律和流行趨勢進行研究，提出閾值理論[1]。隨著細菌和病毒的耐藥性問題日漸嚴重，出現一些新的傳染病[2]。因此，大量的數學模型被用于分析各式各樣的傳染病問題[3]。

SEIR傳染病模型是非常重要的模型，很多人用它研究過麻疹、登革熱等疾病，帶有脈沖接種的流行病模型和具有非線性發生率的模型[4]，已經建立并研究了很多年[5]。本文建立了一個具有脈沖和時滯的模型來描述一類具有脈沖接種和染病潛伏期的疾病[6]，結論是給出了染病者一致持續生存的條件，也就是存在q＞0，使得當t充分大時，I(t)≥q。

1 模型建立

把人群劃分為四類：易感者、潛伏者、染病者、移出者。分別用S(t)、E(t)、I(t)、R(t)表示四類人群在t時刻的數量。總人口數N是漸進穩定的常數，不妨設為1。即S(t)+E(t)+I(t)+R(t)=1。討論SEIR模型：

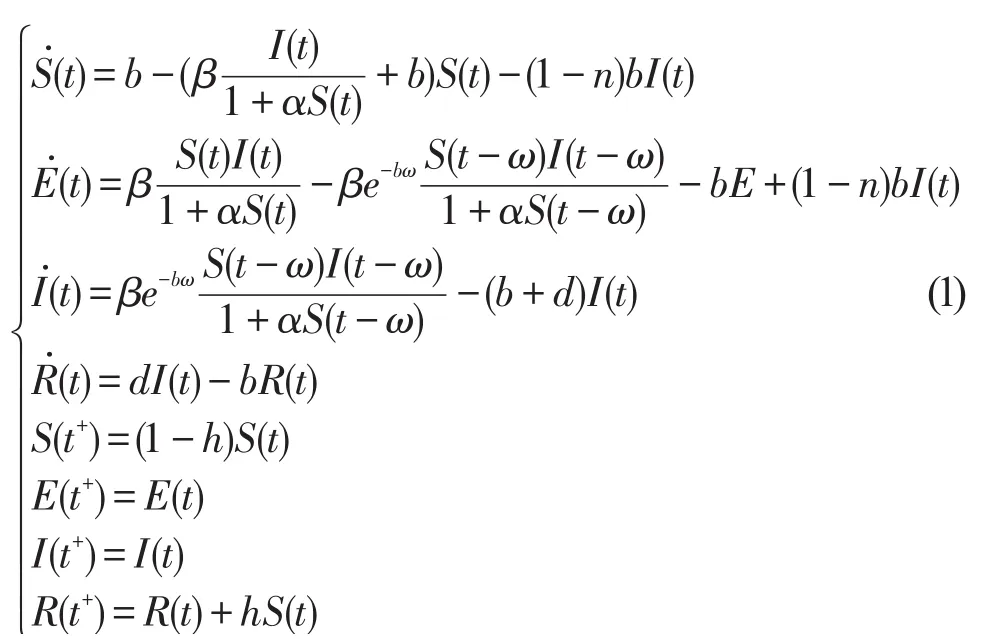
其中b為死亡率，d為恢復率，h為預防接種比率，ω為潛伏期，n(0＜n＜1)為染病者新生兒成為易感者的比例，1-m為染病者新生兒被傳染成為潛伏者的比例。所有系數均為正數。E、R在模型(1)的第一個和第三個方程沒有出現，故只需研究下面的方程組

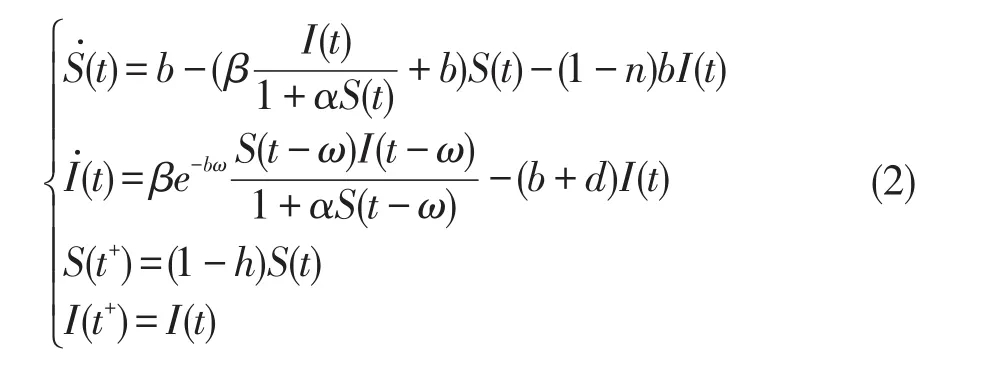
系統(2)的初始條件是

2 持久性

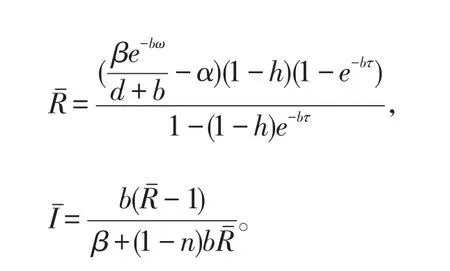
證明系統(2)的第二個方程可以寫作

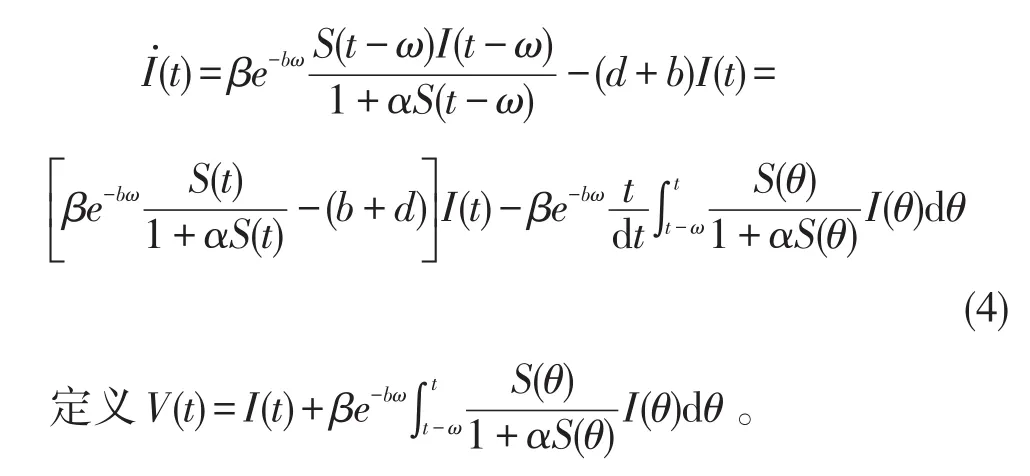
計算V(t)沿著系統(2)的解的導數

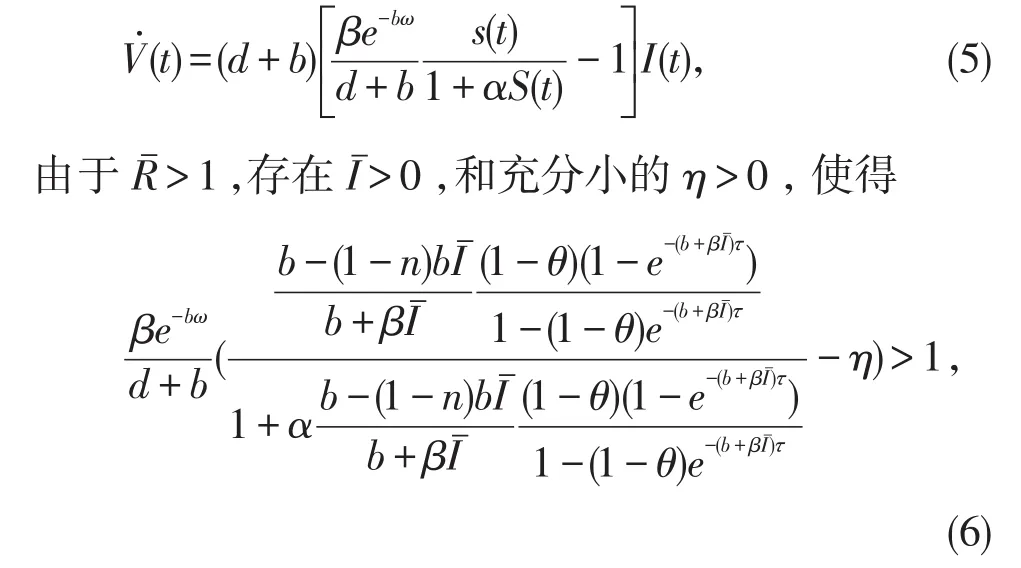
對于任意t0＞0，可以斷言當t≥t0是，I(t)≤不能成立。否則，存在t0＞0,使得當t≥t0時，I(t)≤。由系統(2)的第二個和第三個方程，可得

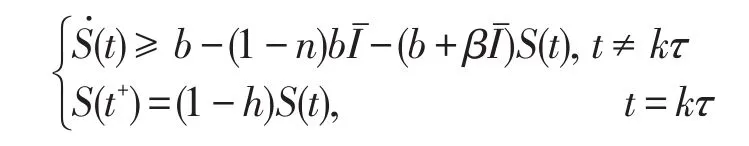
當t＞t0時，考慮下面比較系統

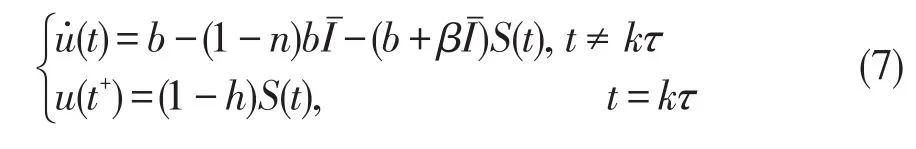
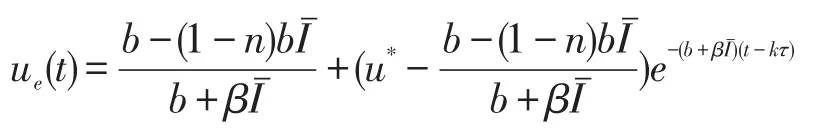
令(S(t),I(t))是系統(2)滿足初始條件(3)和S(0+)=＞0 的解，u(t)是系統（7）滿足u(0+)=＞0 的解，我們知道存在t1(＞t0+ω)，當t≥t1時 ，有

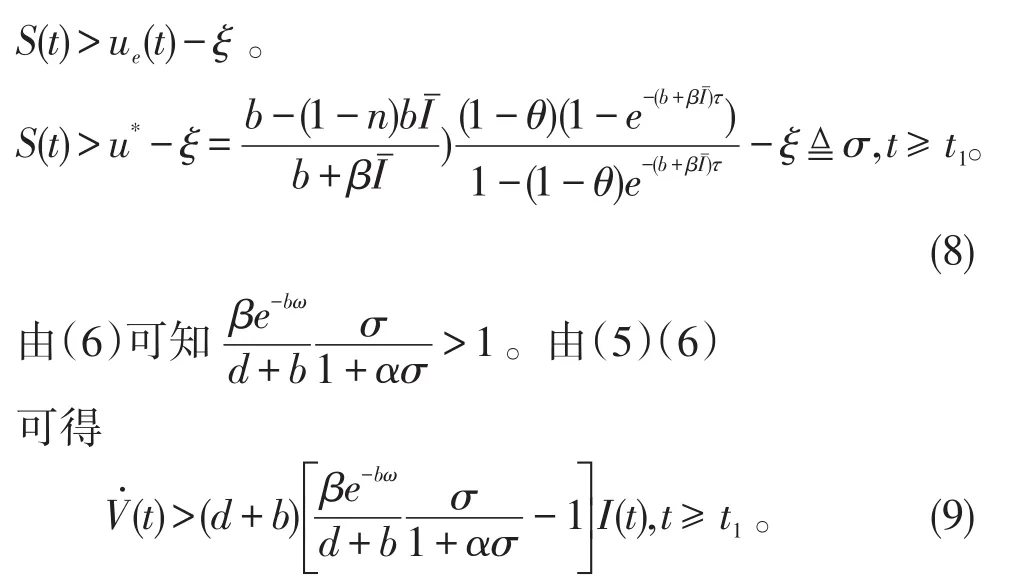
令

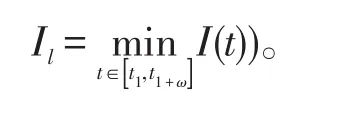
可以斷言對所有的t≥t1，都有I(t)≥Il。否則，存在T0≥0,使 得 當時 ，I(t)≥Il,I(t1+ω+T0)=Il且I˙(t1+ω+T0)≤ 0 。

利用系統(2)的第二個方程和（8）可得

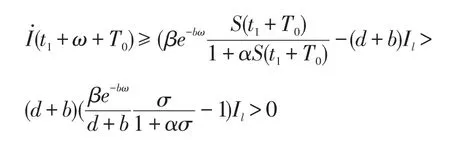
矛盾，所以I(t)≥Il，t≥t1。

由（9）可得

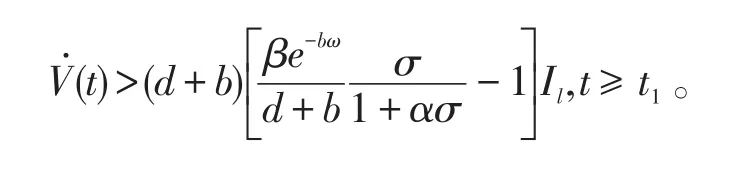
這表明當t→∞時，V(t)→∞。這與當t充分大時V(t)≥，則所要的結果得到。另一方面，如果I(t)關于震蕩，令

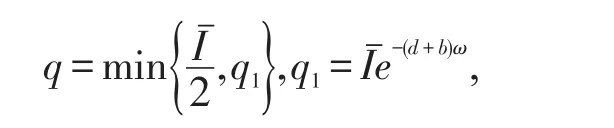
下面證明I(t)≥q，令t*＞0，γ＞0使得I(t*)=I(t*+γ)并且當t*充分大時，有S(t)＞σ,t*＜t＜t*+γ。

由于系統(2)的正解最終有界，I(t)不受脈沖作用可知I(t)是一致連續的。所以存在T(0＜T＜ω,且T的選取與t*無關），使得

如果γ≤T。則所要的結果得到。接下來考慮如果T＜γ≤ω。由系統(2)的第二個方程可得I˙(t)＞-(d+b)I(t)且I(t*)=時，有I(t)≥q1,t*＜t＜t*+γ。如果γ＞ω,由系統(2)的第二個方程可得I(t)≥q,t*＜t＜t*+ω。繼續上面的討論能夠得到I(t)≥q,t*＜t＜t*+γ。由于區間是任取得（僅需要t*充分大），便可以得到I(t)≥q,對所有充分大的t成立。根據上面的討論，q的選擇與系統(2)的正解無關。

證明令(S(t),I(t))是系統(2)的任意一解，由系統(2)的第一個和第三個方程可得

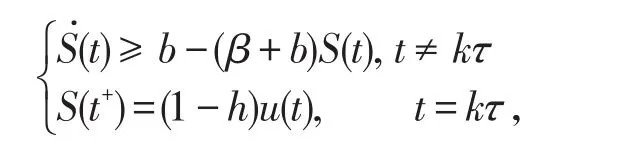
對于充分小ε0＞0，使得

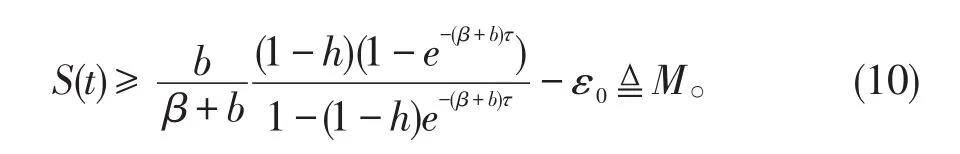
由定理1和定理2我們可以得到下面的結論：令

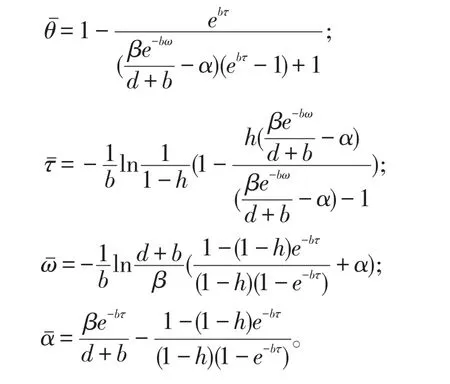
推論 1 如果θ＜或者τ＜或者ω＜或者α＜,則系統(2)是持久的，也就是說疾病會成為地方病平衡點。

3 數值分析與結論

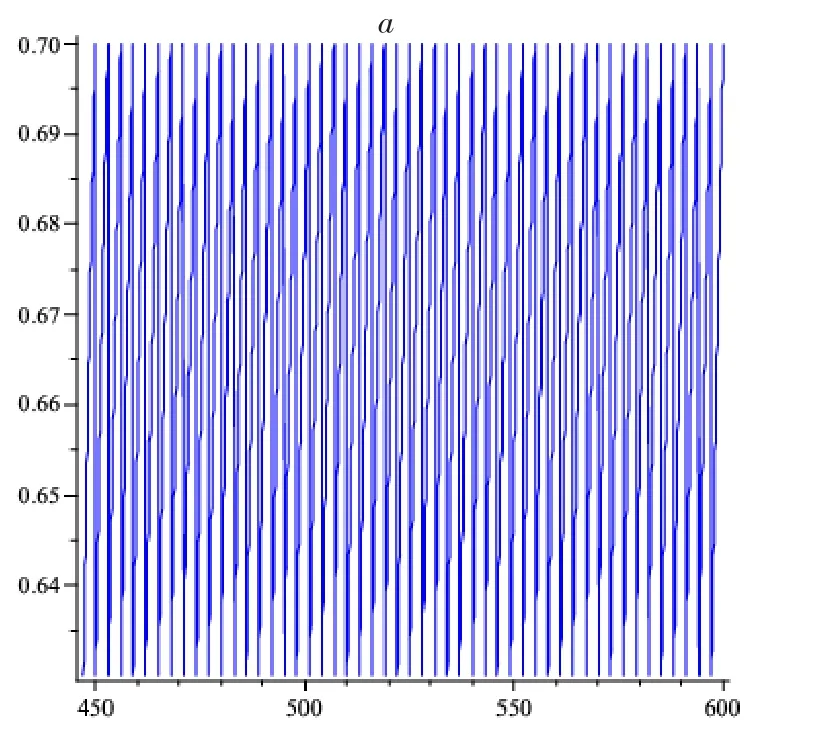
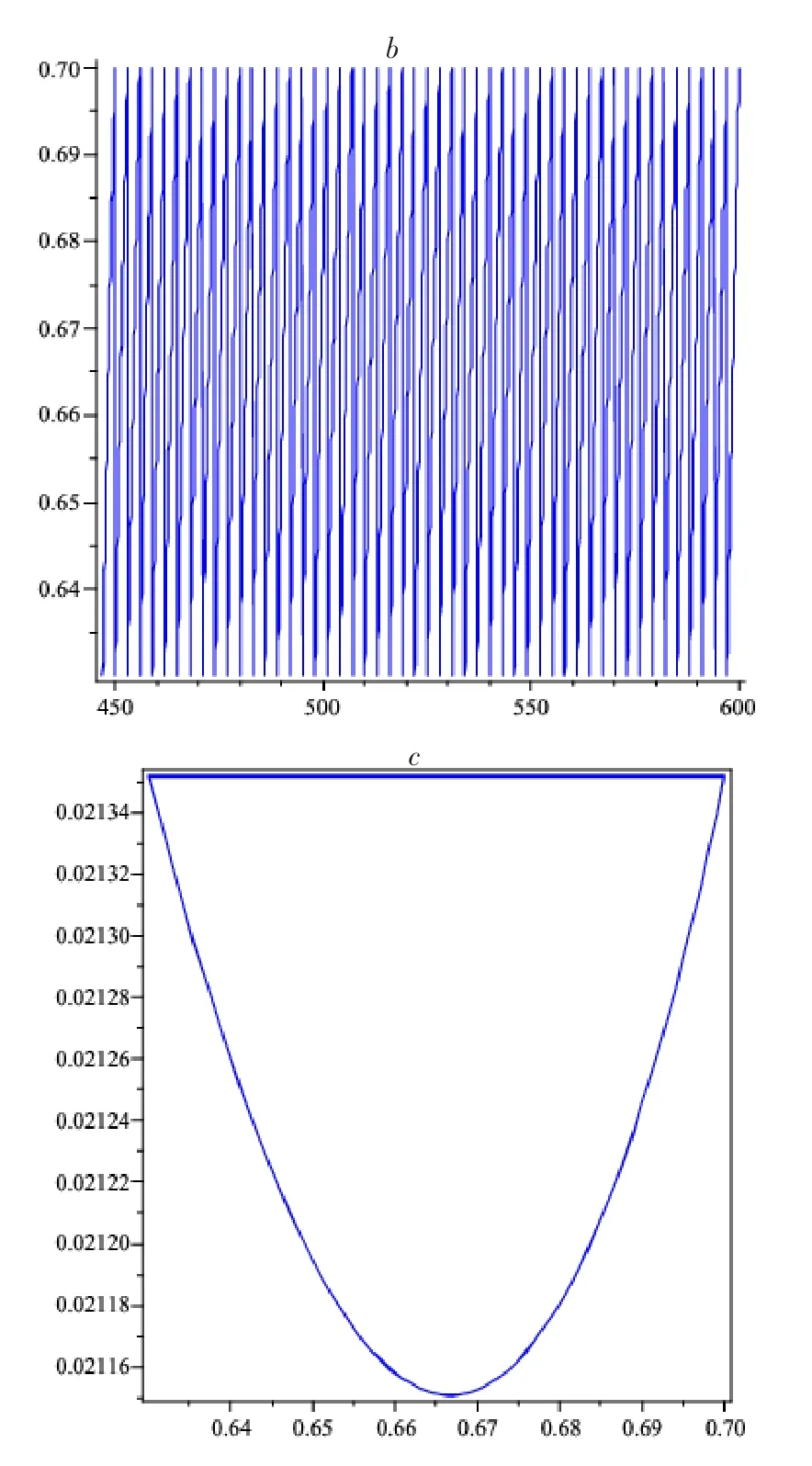
圖1 系統（2）持久性示意圖

圖1：其中a是*=1.2036＞1時，易感者人群時間序列圖;b是*=1.2036＞1時，染病者人群時間序列圖;c是*=1.2036＞1時，系統(2)τ周期解的相圖。

[1]馬知恩，周義倉，王穩地，等.傳染病動力學的數學建模與研究[M].北京：科學出版社，2004.

[2]Iannelli M,Maia Marcheva,Li X Zh.Strain Replacement in an Epidemic Modelwith Perfect Vaccination[J].Mathematical Biosci?ence,2005,195(1):23-46.

[3]Maia Marcheva,Iannelli M,Li X Zh.Competition and Coexistence of Strains:The Impactof Vaccination[J].Mathematical Bioscienc?es and Engineering,2007,4(2):287-317.

[4]Onofrio A D.Stability properties of pulse vaccination strategy in SEIR epidemic model[J].Math Biosci,2002,179:57-72.

[5]L Stonc,B Shulgin,Z Agur.Theoretical examination of the pulse vaccination policy in the SIR epidemic model[J].Math Comput.Modelling,2000(31):207-215.

[6]S Ruan,W Wang.Dynamical behavior of an epidemic model with a nonlinear incidence rate[J].Di ffer.Equat.,2003(188):135-163.

〔責任編輯 高海〕

A SEIR Model with Delay and Pulse Inoculation

TONG Yao-hua1,SHI Yan-ling2
(1.School of Mathematical and Computer Science,Shanxi Datong University,Datong Shanxi,037009;2.Network Information Center,Shanxi Datong University,Datong Shanxi,037009)

In this paper,we established a model with impulsive and delay to describe a class of impulse inoculation and incuba?tion period infected disease.The sufficient co-nditions of system persistence are obtained by applying the theory of delay differential equation and impulse differential equation.

time delay;infectious disease model;balance;pulse vaccination

TQ018

A

1674-0874(2017)05-0015-03

2017-03-26

仝耀華(1979-),女,山西大同人,碩士,講師,研究方向:生物數學。