膜系統下的一種多目標優化算法

屠傳運，陳韜偉，余益民，趙昆

(云南財經大學 信息學院， 云南 昆明 650221)

膜系統下的一種多目標優化算法

屠傳運，陳韜偉，余益民，趙昆

(云南財經大學 信息學院， 云南 昆明 650221)

提出一種基于膜優化理論的多目標優化算法，該算法受膜計算的啟發，結合膜結構、多重集和反應規則來求解多目標優化問題。為了增強算法的適應能力，采用了遺傳算法中的交叉與變異機制，同時在膜中引入外部檔案集，并采用非支配排序和擁擠距離方法對外部檔案集進行更新操作來提高搜索解的多樣性。仿真實驗采用標準的KUR和ZDT系列多目標問題對所提出的算法進行測試，通過該算法得出的非支配解集能夠較好地逼近真實的Pareto前沿，說明所提算法在求解多目標優化問題上具有可行性和有效性。

膜計算;多目標優化;遺傳算法;外部檔案集;非支配排序;擁擠距離;非支配解集;Pareto前沿

在實際生活以及各種工業領域中都會遇到各種多個目標彼此沖突，且在一定條件約束下，但又要求得優化結果的問題，這一類問題被稱為多目標優化問題。為了解決這個問題，近年來一些國內外學者提出了許多基于智能進化計算的求解算法，取得了顯著的成果，并將其應用在了科學研究和工程方面。第1代的多目標優化算法是以Fonseca等[1]于1993年提出的多目標遺傳算法MOGA(multi-objective genetic algorithm )、Srinivas 等[2]提出的非支配排序遺傳算法NSGA(non-dominated sorting genetic algorithm)、Horn等[3]提出的小生境Pareto多目標標優化遺傳算法NPGA (niched pareto genetic algorithm)為主。第2代多目標優化算法主要以精英保留機制為特征，在20世紀末和21世紀初相繼被提出：Zitzler等[4]于1999年提出加強Pareto進化算法(strength pareto evolutionary algorithm，SPEA )，3 年之后,他們提出了SPEA改進版本SPEA2；Erichson等[5]于2001年提出了NPGA 的改進版本NPGA2； 經典且效率極高的NSGA-II算法于2002 年由Deb 等[6]通過對NSGA 進行改進而提出。

膜計算(membrane computing)是自然計算的新分支，旨在從生命細胞的結構與功能以及組織和器官等細胞群的協作中抽象出計算模型[7]。膜計算又被稱為膜系統或P系統，膜計算由歐洲科學院院士Paun于1998年提出，由于其具有分布式和并行計算的能力，目前在將膜計算理論應用于多目標優化問題上獲得了一些研究成果。Zaharie等[8]于2009年通過對比分布式演化算法和膜算法的異同，受膜算法的啟發提出了運用于求解連續優化問題的分布式演化算法；Liu等[9]提出將遺傳算法引入到膜算法，利用遺傳算法的交叉與變異機制，該算法求解ZDT系列優化問題表現出了較好的求解能力；Zhang等[10]提出了將差分演化與P系統相結合的算法，并將其運用于多目標優化問題上。

受到膜計算理論啟發，本文提出了一種結合膜系統理論的多目標優化算法，即基于P系統的遺傳算法(P-genetic algorithm，P-GA)。本文采用的膜系統只具有表層膜和基本膜，將一定數量的種群放入表層膜中，然后經過非支配排序后分配到基本膜中。并在基本膜中運用遺傳機制來求解多目標優化問題的非支配解集，在表層膜中引入NSGA-Ⅱ算法，以此來維持非支配解集的多樣性，采用KUR和ZDT系列多目標測試函數來進行仿真實驗，得出的非支配解集能夠較好地逼近真實的Pareto前沿。本文參考了文獻[11]的設計思路，不同點在于，基本膜中利用通信規則并將交叉與變異的操作進行了改變。

1 多目標優化問題和膜計算理論

1.1 多目標優化問題的數學描述

多目標優化問題有很多種表示方式，用數學方式描述比較直觀，便于理解。不失一般性的描述為

式(1)中有n個決策變量，x={x1,x2,…xn}∈Rn，Rn為n維決策空間；F(x)∈Rm，Rm為m維的目標空間；目標函數F(x)定義了m個由決策空間向目標空間映射的關系；gi(x)=0,i=(1,2,…,q)描述了q個等式約束條件；hj(x)≥0,j=(1,2,…,p)定義了p個不等式約束條件。在以上的描述基礎上，給出以下幾個定義。

定義1 (可行解)對于任意一個x∈Rm，且滿足式(1)中所給出的約束條件，則稱x為可行解。

定義2 (Pareto占優)對所有滿足定義1的可行解組成的集合稱為可行解集合，用X表示，則X?Rn；假設有兩個可行解xa,xb∈X，若xa與xb相比較，xa是Pareto占優的，則條件當且僅當滿足：

記作xalt;xb，也稱為xa支配xb。若xa和xb之間不存在相互支配關系，則稱它們之間非支配。

定義3 (Pareto最優解X*)如果存在一個X*滿足?x∈Rn,xlt;x*，則X*為Pareto最優解，也叫作非支配解；Pareto最優解集定義為所有Pareto最優解組成的集合，記作P。

定義4 (Pareto前沿)最優解集P在目標函數空間上的映射，記作PF，表示為

1.2 膜計算理論

目前，對膜的研究主要包括細胞型、組織型和神經型3種模型[12]。本文所提出的算法是建立在細胞型膜系統上，下面介紹細胞型膜系統理論的主要內容：

根據式(4)的多元組，其中：V是字母表，V中的元素稱為字符對象；T?V，T為輸出的字母表；μ是包含m個膜的膜結構，其中m表示∏的度；wi∈V*，且i=1,2,…,m，表示膜結構μ中第i個膜所包含的字符多重集，V*表示由V中的字符對象組成的任意多重集；R是進化規則的有限集合，進化規則是二元組；Ri(i=1,2,…,m)對應的是膜結構μ中的區域i的進化規則集合。

細胞型膜結構如圖1所示，最外層把細胞膜結構與外界環境隔開的膜稱為表層膜；每一個膜都確定一個區域，區域中包含了反應規則和多重集；對任意一個膜，若該膜區域內不包含其他的膜，即膜中無膜，則稱為基本膜。

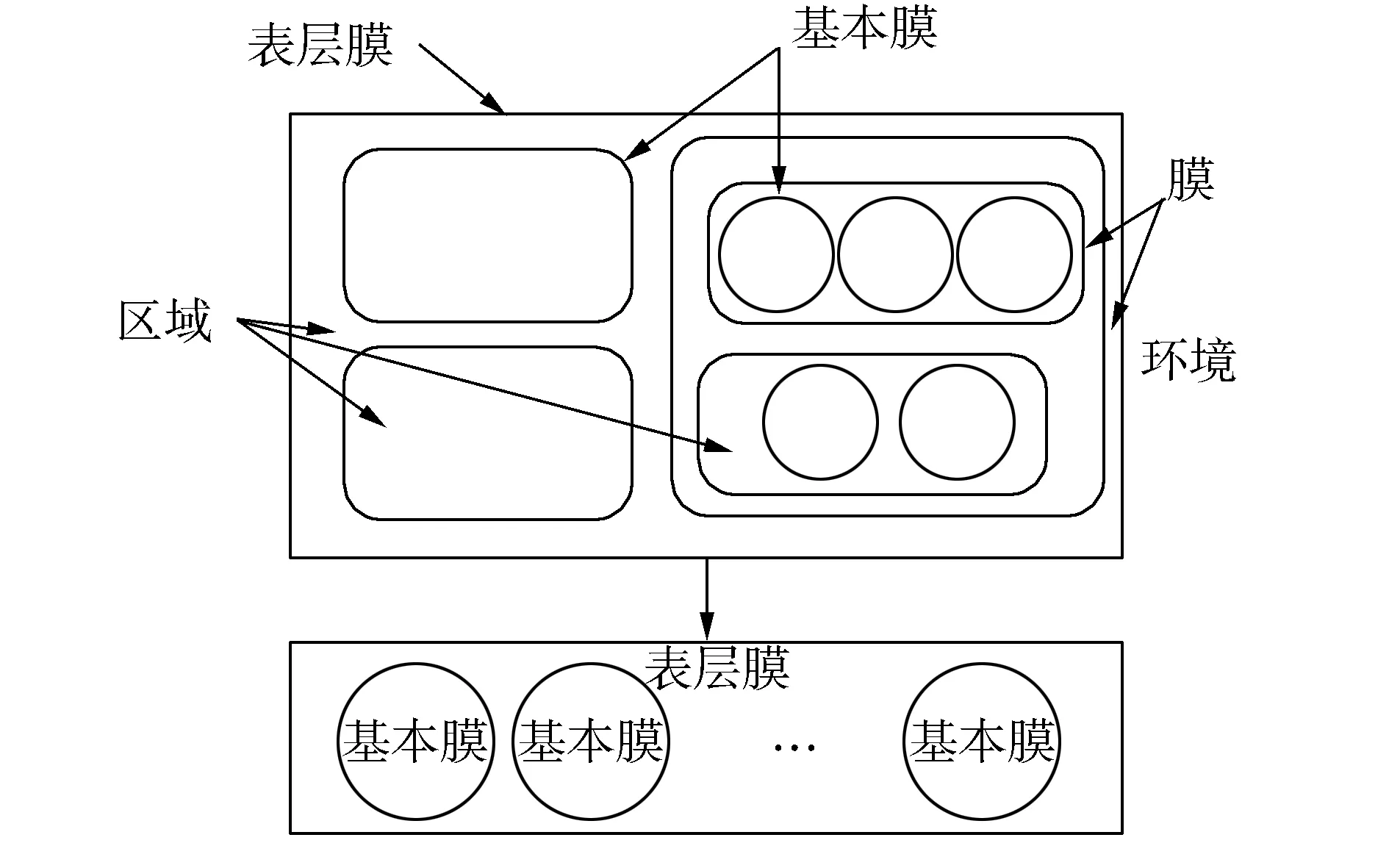
圖1 膜系統與其簡化結構Fig.1 Membrane system with its simplified structure

2 P-GA算法

P系統由字符對象多重集、反應規則和膜結構三部分組成[13]。在P系統中，字符對象與多重集分別對應所求多目標優化問題的解和解集，且每一個字符對象都會通過適應度函數得到一個適應度值；反應規則既是算法具體的執行，也有對細胞膜的操作，比如分裂、溶解等；膜結構的運用使算法具有了分布式和并行計算的能力[14]。在每一次的迭代，將隨機產生的字符對象放入表層膜區域中，利用表層膜區域中的反應規則和通信規則進行操作；最后通過膜的溶解將多重集釋放到表層膜區域中交流信息。為了降低仿真實驗難度，所提算法采用的細胞型膜結構只有表層膜與基本膜，這種二層結構相較于原結構復雜度較低。

為了使算法得出的多重集有較好的多樣性，故引入NSGA-Ⅱ算法，利用其非支配排序和擁擠距離兩種機制來獲得。

遺傳算法(genetic algorithm，GA)是模擬達爾文進化論(適者生存、優勝劣汰遺傳機制)，借鑒生物界的進化規律演化而來的隨機化搜索方法。該方法具有并行性和更好的全局尋優能力[15-16]。

P-GA算法基于膜計算理論，包含了遺傳機制，利用NSGA-Ⅱ算法的非支配排序和擁擠距離兩種機制來設計算法，詳細步驟如下。

1)根據優化問題的約束條件，在表層膜的區域內隨機生成N個字符對象(N≥i≥1)，所有字符對象均為十進制編碼，具體形式為

式中：si,j表示第i個字符對象的第j維；j的范圍為D≥j≥1，D表示維數；smin,j表示第j維的最小值，smax,j表示第j維的最大值；rand()為隨機數函數，產生從0～1的隨機數。

2)根據所要優化問題的目標函數計算出每個字符對象的適應度值，從而完成對所有字符對象的評價。

3)在初始化完成以后，利用表層膜的分裂規則，在表層膜內部區域分裂出m+1個基本膜，且分裂出的基本膜具有求解多目標優化問題的能力。首先，將初始化完成的m個多重集復制一份發送到第m+1個基本膜的區域中；然后，將m個多重集發送到前m個基本膜的區域中，逐一對應。具體表層膜分裂規則如式(6)：

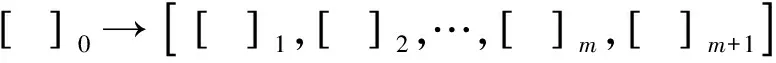
式中：[ ]0表示表層膜，[ ]i表示第i個基本膜。

為了使每個基本膜的內部區域都有對應的多重集，利用NSGA-Ⅱ的非支配排序機制對表層膜區域中的所有字符對象進行排序，排序標準參照2)完成適應值大小，排序結束以后再將其按照等數量劃分為多個子字符多重集。具體劃分的形式化表述如式(7)所示：

式中：w表示字符多重集；sort(w)表示對表層膜區域中的多重集進行非支配排序；wi表示第i個子字符多重集；sizeof(w)表示多重集中字符對象個數；m表示基本膜的個數；n表示每個基本膜取得字符對象個數，具體放入規則對n進行取模。

4)對前m個基本膜用GA算法中的交叉規則進行多線程并行計算，以獲得新的字符對象，而并行計算可以極大地加快求解速度，具體交叉操作為

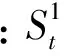
5)利用通信規則將前m個基本膜中產生的交叉結果復制一份發送到第m+1個基本膜中，對第m+1個基本膜中的多重集進行變異操作。由于自然進化中種群變異率往往比較低，因此在一次迭代中，只有利用足夠多的字符對象進行變異操作才能產生更多的新個體，具體變異操作如式(9)所示：

式中：S(t,j)表示字符對象S的第t代j維的值；S(min,j)表示第j維的最小值；S(max,j)表示第j維的最大值；rand( )為隨機數函數，產生從0～1的隨機數。

6)當每個基本膜中的規則和操作都結束以后，調用基本膜區域內的溶解規則，當m+1個基本膜全部溶解后，表層膜區域中就會有來自于不同基本膜中的字符對象；本文引入外部檔案集，將從基本膜中溶解出的字符對象插入到外部檔案集中，而后將表層膜區域中的字符對象與歸入外部檔案的字符對象進行非支配排序操作。外部檔案的執行流程為：①對所有字符對象執行NSGA-Ⅱ算法中的兩種機制；②根據執行結果選取支配等級較低的字符對象，若兩者支配等級相等，則比較擁擠距離大小，選取擁擠距離較大的字符對象；③通過②的選取后，將獲得的所有字符對象歸入外部檔案集，然后刪除檔案中受支配的字符對象，剩余存在于外部檔案集中的字符對象將作為下一代的非支配多重集。

這個操作發揮了膜計算的優勢，即在基本膜之間共享和交換信息，從而提高算法對全局未知解的探索，當然也提高了解的多樣性[11,17]。

7)如果算法不滿足條件，則重復2)～6)的步驟；若算法滿足條件，則終止迭代，此時將表層膜區域中的多重集輸出即可。

具體流程如圖2所示。

圖2 P-GA算法流程圖Fig.2 P-GA algorithm implementation flow chart

3 仿真實驗

3.1 測試函數

為了檢驗所提出的算法是否能夠較好地逼近真實的Pareto前沿，采用了KUR、ZDT1、ZDT2、和ZDT3多目標問題測試函數。這些測試函數可以較好地測試算法在多目標優化問題的表現。

3.2 實驗環境

仿真實驗硬件環境：CPU Intel 酷睿i5-4200H，主頻為3.4 GHz，輔以8 GB內存，操作系統為Windows 10，使用MATLAB R2015B進行編程仿真。本文選用了PESA2算法和SPEA2算法與所提出的P-GA算法進行比較，這兩個算法的具體參數如表1所示。

表1 算法參數設置

表1中，D表示決策變量的維度，本文所提出的P-GA算法群體大小設置為200，表層膜中分裂出11個基本膜，交叉與變異概率均與PESA2算法和SPEA2算法相同。

3.3 仿真結果

KUR測試維度為3，ZDT系列的維度均為30，迭代次數均為100次，測得結果如圖3～6所示。

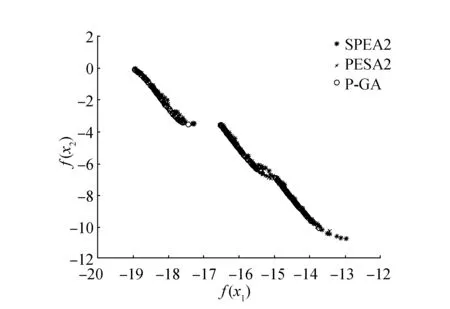
圖3 基于KUR測試函數分布圖Fig.3 KUR test function distribution

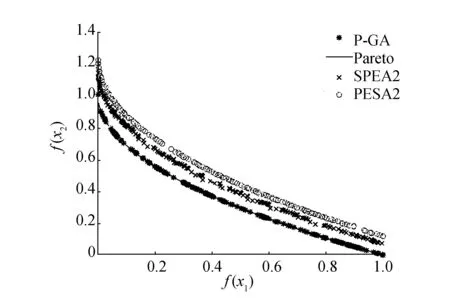
圖4 基于ZDT1測試函數分布圖Fig.4 ZDT1 test function distribution

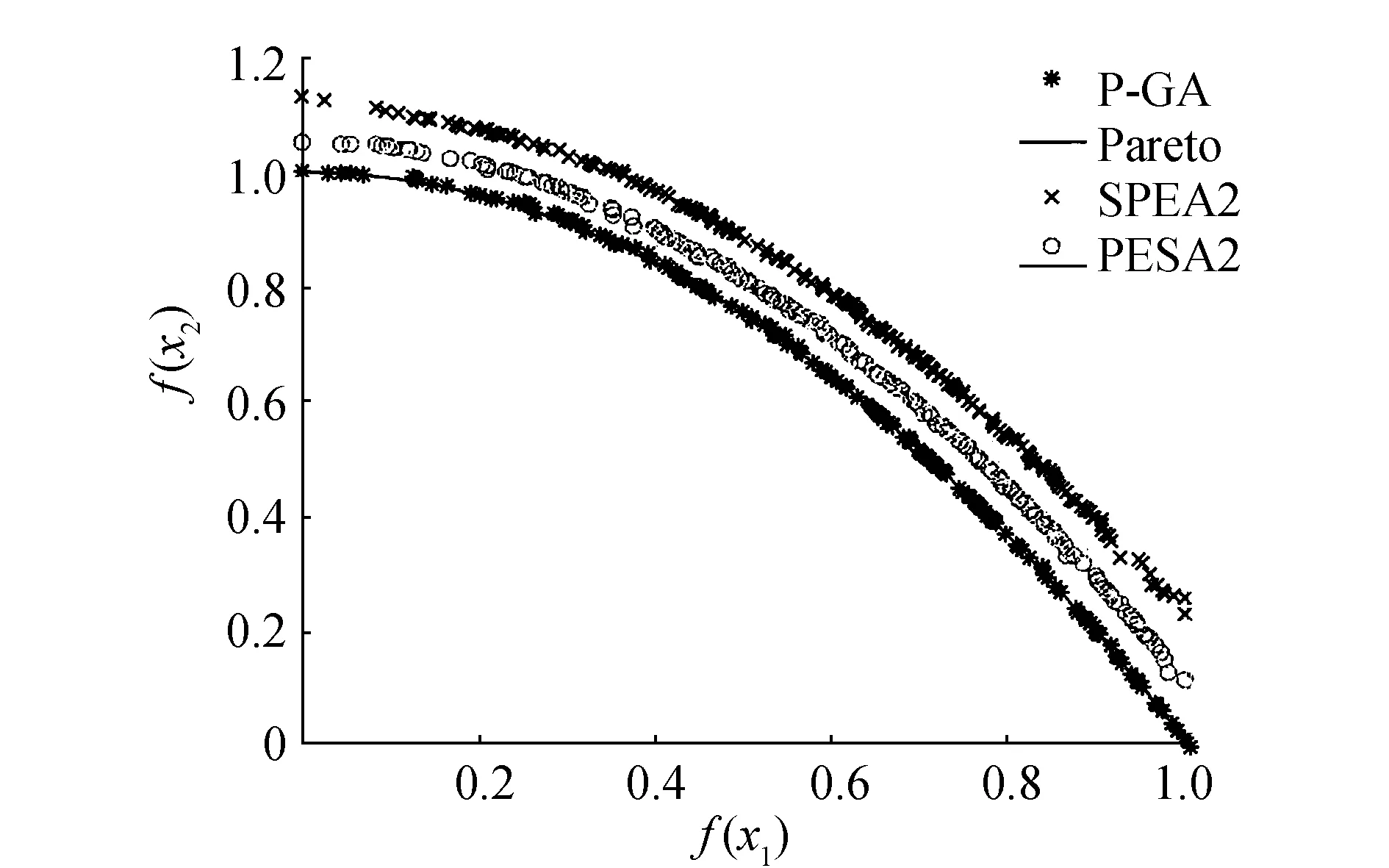
圖5 基于ZDT2測試函數分布Fig.5 ZDT2 test function distribution

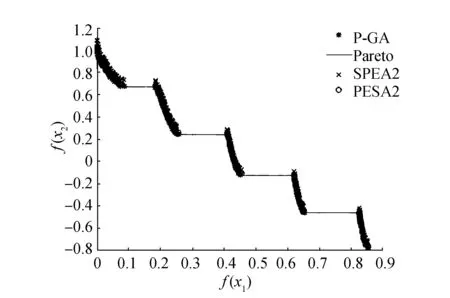
圖6 基于ZDT3測試函數分布Fig.6 ZDT3 test function distribution

從圖3可以看出，PESA2算法與P-GA算法都取得了較好的結果，但P-GA算法較其他兩種算法分散程度較低，而SPEA2效果顯得比較差；通過圖4和圖5可以很直觀地看出P-GA算法能夠較好地逼近真實的Pareto前沿，逼近程度相較于另外兩種算法更高，說明G-PA算法能夠較快地收斂，且分布程度也與另外兩種算法相當，整體上取得的非支配解好于PESA2算法和SPEA2算法；在圖6中可以看出，整體3種算法都取得了較好的效果，都能夠逼近真實的Pareto前沿，且分布離散程度也比較接近。

本文采用反轉時代距離(inverted generational distant,IGD)作為評價指標[18-19]。IGD是度量算法得到的Pareto前沿到真實的Pareto前沿的距離指標，該指標值的大小與算法Pareto前沿收斂性及多樣性呈負相關[20]。通過仿真，得到這3個多目標優化算法在4個測試函數上的數據，其中Mean表示均值，Std.表示標準差，每個算法均在所有測試函數上獨立測試100并進行了統計，表2列出了詳細的統計數據。

表23個算法在4個測試函數上的IGD性能統計

Table2ComparisonofIGDperformanceofthreealgorithmsonfourtestfunctions

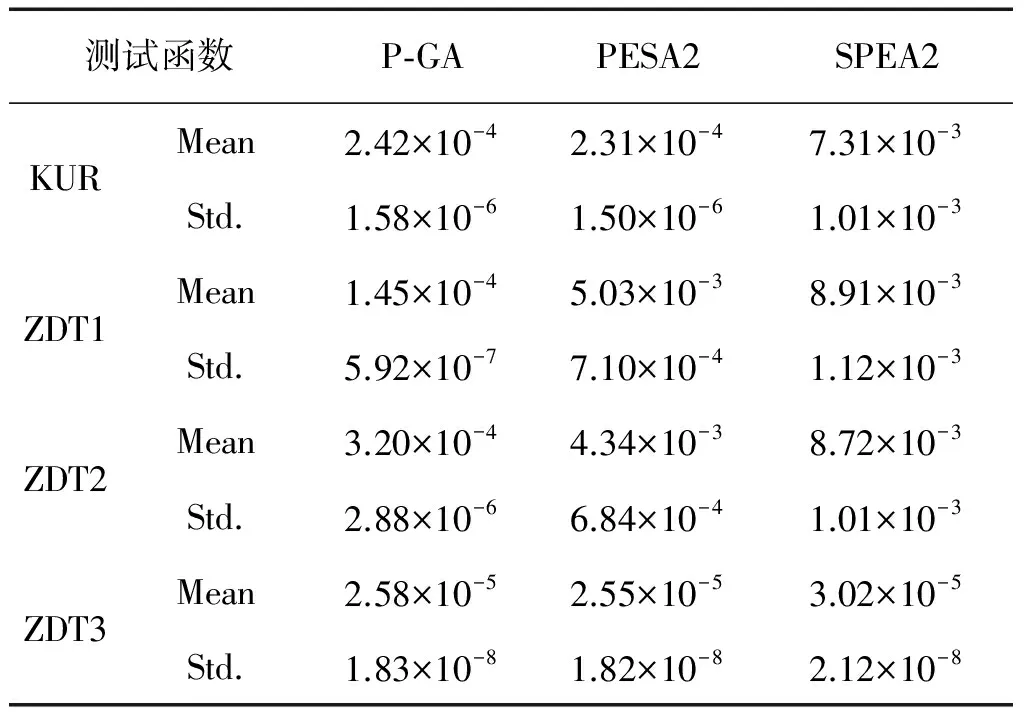
測試函數P?GAPESA2SPEA2KURMean2．42×10-42．31×10-47．31×10-3Std．1．58×10-61．50×10-61．01×10-3ZDT1Mean1．45×10-45．03×10-38．91×10-3Std．5．92×10-77．10×10-41．12×10-3ZDT2Mean3．20×10-44．34×10-38．72×10-3Std．2．88×10-66．84×10-41．01×10-3ZDT3Mean2．58×10-52．55×10-53．02×10-5Std．1．83×10-81．82×10-82．12×10-8

從表2中可以看出，在KUR測試函數上，PESA2算法取得了最好的效果，但P-GA算法獲得統計結果與其相差無幾，SPEA2算法表現最差；P-GA在ZDT1和ZDT2測試函數上獲得的統計數據明顯好于其他兩個算法；3種算法在ZDT3測試函數上IGD均值和標準差結果相近。最后需要強調的是，仿真實驗表明在算法流程迭代次數超過2 000次以后，3種算法在測試函數上取得的IGD指標基本一致，在此就不去列舉了。

4 結束語

本文提出了一種基于膜系統下的一種多目標優化算法——P-GA算法，該算法將膜計算相關理論引入，并采用了遺傳算法中的交叉與變異機制來增加算法適應能力。仿真實驗表明，該算法有精度高、收斂速度快、分布較為均勻等優點。此外，膜優化算法的本質具有分布式和并行計算的執行邏輯，但目前的研究仍局限于串行的工作方式，這也是不足之處。因此，如何實現算法的并行優化計算，也是下一步研究的重點內容和方向。

[1]FONSECA C M, FLEMING P J. Genetic algorithms for multi-objective optimization: formulation, discussion and generalization[C]//The 5th International Conference on Genetic Algorithms. San Mateo，CA, USA, 1993: 416-423.

[2]SRINIVAS N, DEB K. Multi-objective optimization using non-dominated sorting in genetic algorithms[J]. Evolutionary computation, 1994, 2(3): 221-248.

[3]HORN J, NAFPLIOTIS N, GOLDBERG D E. A niched pareto genetic algorithm for multi-objective optimization[C]//Proceedings of the first IEEE Conference on Evolutionary Computation. Orlando, FL, USA, 1994: 82-87.

[4]ZITZLER E, THIELE L. Multi-objective evolutionary algorithms: a comparative case study and the strength Pareto approach [J]. IEEE trans. on evolutionary computation, 1999, 3(4):257-271.

[5]MARK ERICKSON A M, HORN J. The niched pareto genetic algorithm 2 applied to the design of groundwater remediation systems[J]. Lecture notes in computer science, 2001, 1993:681-695.

[6]DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE trans. on evolutionary computation, 2002, 6(2):182-197.

[7]PAUN G, ROZENBERG G. A guide to membrane computing[J]. Theoretical computer science, 2002, 287(1):73-100.

[8]ZAHARIE D, CIOBANU G. Distributed evolutionary algorithms inspired by membranes in solving continuous optimization problems[J]. Lecture notes in computer science, 2009, 4361:536-553.

[9]LIU C, HAN M, WANG X Z. A multi-objective evolutionary algorithm based on membrane systems[C]//Fourth International Workshop on Advanced Computational Intelligence. Wuhan, China, 2011:103-109.

[10]ZHANG G, CHENG J, GHEORGHE M, et al. A hybrid approach based on differential evolution and tissue membrane systems for solving constrained manufacturing parameter optimization problems[J]. Applied soft computing, 2013, 13(3):1528-1542.

[11]韓敏, 劉闖, 邢軍. 一種基于膜系統理論的多目標演算法[J]. 自動化學報, 2014, 40(3):431-438.

HAN Min, LIU Chuang, XING Jun. A multi-objective evolutionary algorithm based on membrane system theory[J]. Acta automatica sinica, 2014, 40(3):431-438.

[12]PAUN G, ROZENBERG G, SALOMAA A. The Oxford handbook of membrane computing [M]. Oxford ：Oxford University Press, 2010.

[13]張葛祥, 潘林強. 自然計算的新分支——膜計算[J]. 計算機學報, 2010, 33(2):208-214.

ZHANG Gexiang, PAN Linqiang. A survey of membrane computing as a new branch of natural computing[J] . Chinese journal of computers, 2010, 33 (2): 208-214.

[14]張葛祥, 程吉祥，王濤，等. 膜計算: 理論與應用 [M]. 北京：科學出版社, 2015.

[15]張玉良. 改進粒子群優化算法在圖像矢量量化中的應用研究[D]. 天津：天津工業大學, 2013.

ZHANG Yuliang. Application of improved particle swarm optimization algorithm in image vector quantization [D]. Tianjin: Tianjin Polytechnic University, 2013.

[16]周明. 遺傳算法原理及應用[M]. 北京：國防工業出版社, 1999.

[17]李俊. 基于膜計算模型的多目標優化算法研究[D]. 合肥：安徽大學, 2016.

LI Jun. Study on Multi-objective Optimization Algorithm Based on Membrane Computing Model [D]. Hefei : Anhui University, 2016.

[18]黃席越, 張著洪, 何傳江,等. 現代智能算法理論及應用[M] . 北京: 科學出版社, 2005.

[19]JU Y, ZHANG S, DING N, et al. Complex network clustering by a multi-objective evolutionary algorithm based on decomposition and membrane structure[J]. Scientific reports, 2016, 6:33870.

[20]ZHANG G, LI Y, GHEORGHE M. A multi-objective membrane algorithm for knapsack problems[C]// IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications. Gwalior, India, 2012:604-609.

屠傳運，男，1992年生，碩士研究生，主要研究方向為多目標優化、膜計算。

陳韜偉，男，1972年生，副教授，博士，主要研究方向為智能信息處理、雷達信號處理及電子商務。主持并參與多項國家級課題，發表學術論文多篇，其中被SCI、EI檢索10余篇。

余益民，男，1968年生，副教授，博士，主要研究方向為跨境電子商務、能源互聯網及數據挖掘技術。主持參與多項國家級課題，發表學術論文30余篇，被SCI、EI檢索10余篇。

Multi-objectiveoptimizationalgorithmbasedonmembranesystem

TU Chuanyun， CHEN Taowei， YU Yimin， ZHAO Kun

(College of Information, Yunnan University of Finance and Economics, Kunming 650221, China )

In this paper, we propose a multi-objective optimization algorithm based on the theory of membrane optimization. Inspired by membrane computing, this algorithm combines membrane structure, multiple sets, and reaction rules to solve multi-objective optimization problems. We employ the crossover and mutation mechanism in this genetic algorithm to enhance its adaptability. We also introduce an external archive set into the membrane and design a non-dominated sorting and crowding distance method to improve the diversity of the global search solution and thereby update the introduced archive. We used multi-objective problems including KUR and ZDT to evaluate the performance of our proposed algorithm. Our results show that the non-dominated solution set derived from the proposed algorithm can better approach the real Pareto front, which confirms that the proposed algorithm is feasible and effective in solving multi-objective optimization problems.

membrane computing; multi-objective optimization; genetic algorithm; external archive set; non-dominated sorting; crowding distance; non-dominated solution set; Pareto front

10.11992/tis.201706013

http://kns.cnki.net/kcms/detail/23.1538.TP.20171021.1351.016.html

TP301

A

1673-4785(2017)05-0678-06

中文引用格式：屠傳運，陳韜偉，余益民，等.膜系統下的一種多目標優化算法J.智能系統學報， 2017, 12(5): 678-683.

英文引用格式：TUChuanyun，CHENTaowei，YUYimin，etal.Multi-objectiveoptimizationalgorithmbasedonmembranesystemJ.CAAItransactionsonintelligentsystems, 2017, 12(5): 678-683.

2017-06-06. < class="emphasis_bold">網絡出版日期

日期：2017-10-21.

國家自然科學基金項目(61461051，71462036)；云南省教育廳一般項目(2015Y278).

陳韜偉.E-mail：cctw33@126.com.