衛(wèi)星導(dǎo)航定位卡爾曼濾波時(shí)延平滑方法研究
劉 成,郭樹人,李 芳
(1. 北京跟蹤與通信技術(shù)研究所,北京100094; 2. 中國(guó)科學(xué)院國(guó)家天文臺(tái),北京 100190)
衛(wèi)星導(dǎo)航定位卡爾曼濾波時(shí)延平滑方法研究
劉 成1,郭樹人1,李 芳2
(1. 北京跟蹤與通信技術(shù)研究所,北京100094; 2. 中國(guó)科學(xué)院國(guó)家天文臺(tái),北京 100190)
為進(jìn)一步提高衛(wèi)星導(dǎo)航定位精度和性能,介紹和討論了卡爾曼濾波延時(shí)平滑方法,并建立了一種卡爾曼濾波延時(shí)平滑定位模型與算法。與經(jīng)典卡爾曼濾波類似,該算法同樣具有狀態(tài)系統(tǒng)與測(cè)量系統(tǒng)兩類方程,能夠根據(jù)后續(xù)歷元測(cè)量值及定位結(jié)果向前進(jìn)行逆向預(yù)測(cè)與更新,從而達(dá)到對(duì)整體定位過(guò)程再次平滑的目的,更大程度地獲得定位結(jié)果跟隨性與平滑性之間的平衡。通過(guò)多種不同情況下的GPS實(shí)測(cè)試驗(yàn),對(duì)方法的正確性和可行性進(jìn)行了分析與驗(yàn)證。結(jié)果表明,卡爾曼濾波延時(shí)平滑定位方法能夠適用于多種靜態(tài)、動(dòng)態(tài)導(dǎo)航應(yīng)用領(lǐng)域,使輸出結(jié)果更為平滑和準(zhǔn)確,在有效提高定位精度的同時(shí)具有更強(qiáng)的抗多徑和抗干擾性。
GPS;衛(wèi)星導(dǎo)航定位;卡爾曼濾波;固定時(shí)刻平滑;固定時(shí)延平滑;車載導(dǎo)航
卡爾曼濾波(Kalman filtering)方法[1]對(duì)衛(wèi)星導(dǎo)航定位具有重要意義。基于物體運(yùn)動(dòng)遵循慣性定律這一基本事實(shí),它利用合適的運(yùn)動(dòng)模型,將相鄰時(shí)刻的位置狀態(tài)聯(lián)系起來(lái),從而克服最小二乘法在不同時(shí)刻的定位值互不關(guān)聯(lián)這一缺點(diǎn),將原本孤立雜亂的解結(jié)合起來(lái),使濾波定位結(jié)果更為平滑和準(zhǔn)確[2-4]。因此,卡爾曼濾波及其擴(kuò)展卡爾曼濾波[5]、線性化卡爾曼濾波[6]、不敏卡爾曼濾波[7]等在衛(wèi)星導(dǎo)航中得到了廣泛的應(yīng)用,并不斷發(fā)展完善。
卡爾曼濾波通過(guò)狀態(tài)方程一步轉(zhuǎn)移實(shí)現(xiàn)系統(tǒng)狀態(tài)的預(yù)測(cè)與更新,能夠?qū)崟r(shí)獲得用戶位置。然而,它在“跟隨(tracking)”與“平滑(smoothing)”兩個(gè)特征之間仍然存在著矛盾。實(shí)際應(yīng)用中,往往通過(guò)調(diào)整濾波參數(shù)來(lái)實(shí)現(xiàn)這種平衡。如通過(guò)將濾波中狀態(tài)噪聲或測(cè)量噪聲的協(xié)方差矩陣系數(shù)刻意調(diào)大,可降低測(cè)量值權(quán)重[8-9],從而使濾波結(jié)果更加平滑。但一方面,為保證良好的跟隨性,反映出最小二乘解的真實(shí)性,濾波結(jié)果往往容易顯得不夠平滑,仍具有最小二乘解的雜亂性;另一方面,為追求良好的平滑性,使濾波結(jié)果更為美觀,則又容易導(dǎo)致其偏離用戶真實(shí)位置,產(chǎn)生“失真”的感覺(jué)。
基于卡爾曼濾波原理的延時(shí)平滑方法能夠很好地解決這一問(wèn)題。與根據(jù)經(jīng)驗(yàn)和測(cè)試結(jié)果人為調(diào)整濾波參數(shù)不同,延時(shí)平滑方法從卡爾曼濾波模型出發(fā)進(jìn)行理論公式推導(dǎo),具有嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)性,能夠根據(jù)后續(xù)測(cè)量值及定位結(jié)果進(jìn)行反饋與修正,達(dá)到對(duì)整個(gè)定位過(guò)程再次平滑的目的。它適用于許多對(duì)實(shí)時(shí)性要求不甚敏感的導(dǎo)航應(yīng)用領(lǐng)域,如靜止定位、行人定位、健康與運(yùn)動(dòng)監(jiān)測(cè)、交通路況分析與規(guī)劃等;甚至在實(shí)時(shí)車載定位的某些情況下,由于車輛并非一直處于高速行駛狀態(tài),因此也能夠獲得應(yīng)用。
本文從卡爾曼濾波基本原理出發(fā),介紹卡爾曼濾波延時(shí)平滑方法,分析和討論其理論推導(dǎo)過(guò)程,并由此提出一類衛(wèi)星導(dǎo)航定位中的卡爾曼濾波延時(shí)平滑方法。該方法能夠根據(jù)后續(xù)歷元測(cè)量值及定位結(jié)果向前進(jìn)行逆向預(yù)測(cè)與更新,具有狀態(tài)系統(tǒng)與測(cè)量系統(tǒng)兩類方程;能夠獲得跟隨與平滑之間的良好平衡,使定位結(jié)果更加準(zhǔn)確和平滑。此外,由于可以使用后續(xù)狀態(tài)量及測(cè)量值,因此方法具有更高的抗多徑和抗遮擋性,能夠進(jìn)一步提高定位精度與性能。最后,通過(guò)靜止定位、動(dòng)態(tài)定位等多種不同情況下的GPS實(shí)測(cè)試驗(yàn),對(duì)該方法進(jìn)行分析與驗(yàn)證,以證明其正確性與可行性。
1 卡爾曼濾波定位方法
1.1 卡爾曼濾波回顧
卡爾曼濾波自1960年被提出以來(lái),不斷得到完善和發(fā)展,已廣泛應(yīng)用于各個(gè)領(lǐng)域的信號(hào)與數(shù)據(jù)處理中。有關(guān)卡爾曼濾波的文獻(xiàn)也相當(dāng)豐富,且涉及隨機(jī)變量、隨機(jī)過(guò)程等多方面的知識(shí)和內(nèi)容。因此,本文在此僅作簡(jiǎn)要回顧,不作具體推導(dǎo)。
對(duì)于如下形式的狀態(tài)空間模型[10-11]
(1)
式中,xi、yi分別為系統(tǒng)狀態(tài)與測(cè)量向量;ni、vi分別為狀態(tài)噪聲與測(cè)量噪聲向量;Fi、Gi與Hi分別為系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣、輸入關(guān)系矩陣與測(cè)量關(guān)系矩陣。卡爾曼濾波假定ni和vi為零均值、不相關(guān)的高斯白噪聲,即滿足
(2)
式中,Qi、Ri分別為ni和vi的協(xié)方差矩陣;δij為克羅內(nèi)克函數(shù)(Kronecker Delta)。

測(cè)量更新方程
(3)
時(shí)間更新方程
(4)

1.2 卡爾曼濾波定位模型
衛(wèi)星導(dǎo)航遵循所有運(yùn)動(dòng)物體都符合牛頓定律這一基本事實(shí),因此卡爾曼濾波定位模型可通過(guò)對(duì)不同運(yùn)動(dòng)特點(diǎn)的用戶采用不同的狀態(tài)方程模型來(lái)進(jìn)行描述和實(shí)現(xiàn)。運(yùn)動(dòng)狀態(tài)方程既要盡可能真實(shí)、完整地描述用戶運(yùn)動(dòng)狀態(tài),又要控制狀態(tài)向量的維數(shù),減少計(jì)算量。
對(duì)于行人、汽車、艦船等低動(dòng)態(tài)載體而言,其運(yùn)動(dòng)狀態(tài)一般可用8個(gè)狀態(tài)變量來(lái)描述,即3個(gè)位置分量(x,y,z)、3個(gè)速度分量(vx,vy,vz)和2個(gè)接收機(jī)鐘差變量(δtu,δfu)。該運(yùn)動(dòng)模型因不考慮載體機(jī)動(dòng)因素,因此又稱為常速運(yùn)動(dòng)模型。其狀態(tài)向量為[2,12-14]
x=[xyzvxvyvzδtuδfu]T
(5)
根據(jù)所采用的運(yùn)動(dòng)狀態(tài)模型,其常系數(shù)狀態(tài)轉(zhuǎn)移矩陣F為
(6)

狀態(tài)噪聲協(xié)方差矩陣Q為
(7)

在實(shí)際應(yīng)用中,準(zhǔn)確確定狀態(tài)量噪聲與測(cè)量值噪聲的均方誤差Q、R并不容易。對(duì)于狀態(tài)噪聲誤差Q,一方面可參考接收機(jī)說(shuō)明書及性能測(cè)試指標(biāo)等有關(guān)數(shù)據(jù),另一方面可對(duì)此噪聲信號(hào)作自相關(guān)運(yùn)算來(lái)進(jìn)行估計(jì)。而對(duì)于測(cè)量值噪聲誤差R,可根據(jù)導(dǎo)航電文中的URA值、衛(wèi)星仰角、信號(hào)強(qiáng)度、接收機(jī)信號(hào)跟蹤狀況等信息進(jìn)行估算,在實(shí)踐中也可通過(guò)試驗(yàn)來(lái)測(cè)定測(cè)量誤差方差,然后建立一個(gè)關(guān)于信號(hào)信噪比或衛(wèi)星仰角的測(cè)量誤差方差函數(shù)[2,12]。
2 卡爾曼濾波時(shí)延平滑方法
2.1 固定時(shí)刻平滑
根據(jù)式(4)中的卡爾曼濾波時(shí)間更新方程,可遞推得知當(dāng)i0>i時(shí)有[10]
(8)
式(8)即可視為利用狀態(tài)轉(zhuǎn)移矩陣對(duì)狀態(tài)量未來(lái)的狀態(tài)進(jìn)行i0-i步預(yù)測(cè)。現(xiàn)在,反過(guò)來(lái)考慮i0 (9) 其協(xié)方差矩陣為 (10) 由修正量的正交性原則可推導(dǎo)得[15] (11) (12) 對(duì)于如式(1)給出的一個(gè)標(biāo)準(zhǔn)的狀態(tài)空間模型,當(dāng)j≥i時(shí)有 (13) 對(duì)式(13)進(jìn)行矩陣求逆可得 (14) 再定義矩陣 (15) (16) (17) 將式(17)代入式(16)可得 (18) 由式(12)和式(3)、式(4)可得當(dāng)i≥i0時(shí)有 (19) (20) 結(jié)合式(19)、式(20)可得協(xié)方差矩陣 (21) 為計(jì)算矩陣M的遞推公式,由式(13)—式(15)可推導(dǎo)得到 (22) 再將式(15)代入式(22)即有 (23) (24) 式中,協(xié)方差P提供了平滑值的誤差特征情況。事實(shí)上它只是數(shù)學(xué)上的存在,在整個(gè)遞推計(jì)算過(guò)程中是非必需的,但實(shí)際使用中也可利用它進(jìn)行數(shù)值正確性的監(jiān)測(cè)與檢驗(yàn)。 圖1 卡爾曼濾波延時(shí)平滑計(jì)算流程 卡爾曼延時(shí)平滑定位方法既可應(yīng)用于靜止定位情況,也可應(yīng)用于車載定位等動(dòng)態(tài)情況,以及定位數(shù)據(jù)事后處理與分析等領(lǐng)域。 以靜止定位數(shù)據(jù)處理為例,往往通過(guò)對(duì)一段時(shí)間的定位數(shù)據(jù)取平均來(lái)獲得當(dāng)前位置更精確的坐標(biāo)值。然而,由于接收機(jī)測(cè)量精度及衛(wèi)星星座幾何分布都并非固定不變的,因此定位結(jié)果之間往往并不具有相同的誤差分布,從而使得這種籠統(tǒng)的均值處理方法顯得過(guò)于粗糙。另外,由于缺乏誤差特征指標(biāo),因此當(dāng)測(cè)量或定位出現(xiàn)粗差時(shí)也難以及時(shí)發(fā)現(xiàn)。基于卡爾曼濾波原理的平滑計(jì)算方法則不同,它具有嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)原理及模型,不同時(shí)刻的測(cè)量精度及衛(wèi)星分布信息均包含在協(xié)方差矩陣Pj|j-1和Pj|j中。因此,在連貫的誤差指標(biāo)指引下,它能夠獲得最優(yōu)的遞歸最小二乘平滑結(jié)果,并且具有較強(qiáng)的抗差性。 利用搭載由中科微電子有限公司研制與提供的ATGM332D定位芯片的衛(wèi)星導(dǎo)航接收機(jī)模塊,以1 Hz頻率通過(guò)串口傳輸方式輸出GPS衛(wèi)星廣播星歷及單頻、C/A碼偽距觀測(cè)數(shù)據(jù)。基于該模塊及其測(cè)量輸出進(jìn)行Arm編程實(shí)現(xiàn),并在北京市中科院奧運(yùn)村科學(xué)園區(qū)進(jìn)行實(shí)時(shí)定位試驗(yàn)。 首先,在園區(qū)已知坐標(biāo)點(diǎn)上進(jìn)行了時(shí)間約2 h的靜止定位測(cè)量,按照?qǐng)D1中流程分別采用固定延時(shí)L為1、5、10及30 min的卡爾曼延時(shí)平滑方法進(jìn)行處理,并將其與實(shí)時(shí)卡爾曼濾波定位結(jié)果相比較,如圖2所示。 圖2 靜止定位結(jié)果比較 統(tǒng)計(jì)各類處理方法誤差特征,結(jié)果見表1。 表1 各濾波定位方法均方誤差統(tǒng)計(jì) m 圖2及表1中的試驗(yàn)結(jié)果驗(yàn)證了該方法的正確性和有效性。從中也可以看出,該方法特別適用于靜止定位處理領(lǐng)域,能夠顯著改善定位精度。并且,其效果一般與延時(shí)時(shí)間成正比;隨著可容忍的延時(shí)時(shí)間的增加,定位精度也隨之提高。 同樣基于固定時(shí)延平滑方法在中科院奧運(yùn)村園區(qū)的道路上進(jìn)行了車載定位試驗(yàn),并實(shí)時(shí)計(jì)算和顯示定位結(jié)果。然后,分別采用固定延時(shí)L為1、3、10 s的卡爾曼延時(shí)平滑方法進(jìn)行處理,并與實(shí)時(shí)卡爾曼濾波定位結(jié)果相比較,如圖3所示。 圖3 動(dòng)態(tài)定位結(jié)果比較 從圖3可以看出,即使固定延時(shí)僅為1個(gè)歷元,平滑結(jié)果與實(shí)時(shí)濾波定位結(jié)果之間仍然具有一定的區(qū)別,但效果還不夠明顯。而當(dāng)延時(shí)時(shí)間增加至10個(gè)歷元時(shí),即可明顯看出兩者之間的差別,從圖3中所標(biāo)識(shí)的1、2、3、4號(hào)等位置觀察得尤為明顯。其中,固定時(shí)延平滑結(jié)果要比實(shí)時(shí)濾波定位結(jié)果更平滑,與實(shí)際行駛道路更為吻合,抗遮擋及多徑環(huán)境的性能也更加優(yōu)秀。 在導(dǎo)航數(shù)據(jù)處理中,需要追求定位結(jié)果跟隨性與平滑性之間的平衡。即在使得位置結(jié)果盡量平滑、準(zhǔn)確和美觀的同時(shí),又不損失用戶真實(shí)運(yùn)動(dòng)軌跡的細(xì)節(jié)特征,不造成失真。卡爾曼濾波延時(shí)平滑方法可以很好地解決這個(gè)問(wèn)題,它具體包括固定時(shí)刻平滑與固定時(shí)延平滑方法。與人為根據(jù)經(jīng)驗(yàn)和測(cè)試結(jié)果去調(diào)整濾波器參數(shù)不同,延時(shí)平滑方法同樣具有狀態(tài)更新和時(shí)間更新兩類系統(tǒng)和方程,相當(dāng)于再逆向進(jìn)行了一次卡爾曼濾波過(guò)程,具有嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)性。 具體而言,這種卡爾曼濾波延時(shí)平滑定位方法具有以下幾個(gè)特點(diǎn): (1) 由卡爾曼濾波理論出發(fā)推導(dǎo)得到,其原理和形式均與經(jīng)典卡爾曼濾波方法保持一致,數(shù)學(xué)上嚴(yán)謹(jǐn)、規(guī)范。 (2) 與人為調(diào)整和修改參數(shù)不同,通過(guò)向前逆向預(yù)測(cè)和更新來(lái)對(duì)先驗(yàn)歷元定位進(jìn)行平滑,能夠在進(jìn)一步平滑結(jié)果、減小隨機(jī)誤差的同時(shí),不造成平滑過(guò)度和失真。 (3) 在計(jì)算量與耗時(shí)上,由于延時(shí)平滑方法遞推公式基于狀態(tài)一步轉(zhuǎn)移,因此可以很快向前計(jì)算,不會(huì)造成明顯計(jì)算負(fù)荷。 (4) 模型時(shí)延長(zhǎng)度可根據(jù)實(shí)際應(yīng)用情況進(jìn)行適應(yīng)與更改。 通過(guò)不同情況下的GPS實(shí)測(cè)試驗(yàn),驗(yàn)證、分析了卡爾曼濾波延時(shí)平滑定位方法的正確性和可行性。它不僅能夠在靜止定位或數(shù)據(jù)后處理時(shí)大幅提高定位精度、縮短工作時(shí)間,還能在行人、車載等實(shí)時(shí)動(dòng)態(tài)定位領(lǐng)域根據(jù)實(shí)際情況調(diào)整延時(shí)長(zhǎng)度,更好地獲得定位結(jié)果跟隨與平滑之間的平衡,并同時(shí)具有更強(qiáng)的抗多徑與遮擋的能力。該方法原理嚴(yán)謹(jǐn)、易于實(shí)現(xiàn),具有良好的實(shí)用效果與價(jià)值。 [1] KALMAN R.A New Approach to Linear Filtering and Prediction Problems[J].Transactions of ASME—Journal of Basic Engineering,1960(82):34-45. [2] 謝鋼.GPS原理與接收機(jī)設(shè)計(jì)[M].北京:電子工業(yè)出版社,2009. [3] SORENSON W.Least-squares Estimation:from Gauss to Kalman[J].IEEE Spectrum,1970,7(7):63-68. [4] TED B,RAMA C.Estimation of Object Motion Parameters from Noisy Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8 (1):90-99. [5] WELCH G,BISHOP G.An Introduction to the Kalman Filter[M].Ashville:University of North Carolina,2004. [6] FARRELL J,BARTH M.The Global Positioning System and Inertial Navigation[M].New York:McGraw-Hill,1999. [7] JULIER S,UHLMANN J.A New Extension of the Kalman Filter to Nonlinear Systems[C] ∥Proceedings of AeroSense:The 11th International Symposium on Aerospace/Defense Sensing,Simulation and Controls.Orlando,F(xiàn)L:[s.n.],1997:192-193. [8] GREWAL M,ANDREWS A.Kalman Filtering: Theory and Practice Using MATLAB[M]. 2nd ed. New York:John Wiley & Sons,Inc,2001. [9] 季海福.基于SIGSO同行衛(wèi)星的導(dǎo)航星座原理與算法研究[M].北京:中國(guó)科學(xué)院國(guó)家天文臺(tái),2013. [10] CATTIVELLI F,SAYED A.Diffusion Strategies for Distributed Kalman Filtering and Smoothing[J].IEEE Transactions on Automatic Control,2010,55(9):2069-2084. [11] SAYED H,KAILATH T.A State-space Approach to Adaptive RLS Filtering[J].IEEE Signal Processing Magazine,1994,11(3):18-60. [12] PARKINSON B,SPILKER J,AXELRAD P,et al.Global Positioning System:Theory and Applications[M].[S.l.]: American Institute of Aeronautics and Astronautics,1996. [13] LEANDRO R,SANTOS M.Stochastic Models for GPS Positioning:An Empirical Approach[J].GPS World,2007. [14] HIDE C,MOORE T,HILL C,et al.Low Cost,High Accuracy Positioning in Urban Environments[J].Journal of Navigation,2006, 59(3):365-379. [15] KAILATH T,SAYED H,HASSIBI B.Linear Estimation[M].New Jersey:Prentice Hall,2000. [16] KELLY C,ANDERSON B.On the Stability of Fixed-lag Smoothing Algorithms[J].Journal of the Franklin Institute,1971,291(4):271-281. [17] CATTIVELLI F,LOPES C,SAYED A.Diffusion Strategies for Distributed Kalman Filtering:Formulation and Performance Analysis[C]∥ Proceedings of Cognitive Information. Santorini:[s.n.],2008. StudyonKalmanFilteringTime-lagSmoothingMethodinSatellitePositioning LIU Cheng1,GUO Shuren1,LI Fang2 (1. Beijing Institute of Tracking and Telecommunication Technology,Beijing 100094,China; 2. National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100190,China) In order to improve the accuracy and performance of satellite navigation positioning,a method of Kalman filtering time-lag smoothing was introduced and discussed,and a Kalman filtering smoothing positioning model and its algorithm were built in this paper.Similar to classical Kalman filteing,the algorithm also has two kinds of equations—status system and measuring system,which could help to predict and update backward on the basis of follow-up epoch measured values and positioning results,thereby the overall positioning process can be smoothed again so that we can obtain the balance between positioning result tracking and smoothing performance.The paper analyzed and verified validity and feasibility of the method on the basis of GPS field experiment in various circumstances.Experiment results indicate that Kalman filtering time-lag smoothing positioning method can be adopted in various static and dynamic state navigation application field,which could make position results more smooth and accurate.The method has better anti-multipath and anti-interference performance, and it could also effectively improve positioning accuracy. GPS; satellite navigation and positioning; Kalman filtering; fixed-point smoother; fixed-lag smoother; vehicle navigation 劉成,郭樹人,李芳.衛(wèi)星導(dǎo)航定位卡爾曼濾波時(shí)延平滑方法研究[J].測(cè)繪通報(bào),2017(11):6-10. 10.13474/j.cnki.11-2246.2017.0338. P228 A 0494-0911(2017)11-0006-05 2017-02-22 國(guó)家自然科學(xué)基金(61601009) 劉 成(1987—),男,博士,助理研究員,主要從事衛(wèi)星導(dǎo)航與空間技術(shù)研究工作。E-mail:liucheng@beidou.gov.cn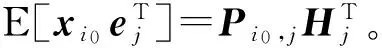






2.2 固定時(shí)延平滑
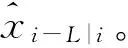

2.3 卡爾曼濾波時(shí)延平滑定位流程


3 試驗(yàn)與分析
3.1 靜止定位試驗(yàn)


3.2 動(dòng)態(tài)定位試驗(yàn)

4 結(jié) 論

