針對雜波抑制的超寬帶MIMO雷達自適應波形設計

季晨荷，宋耀良

(南京理工大學 電子工程與光電技術學院， 江蘇 南京 210094)

針對雜波抑制的超寬帶MIMO雷達自適應波形設計

季晨荷，宋耀良

(南京理工大學 電子工程與光電技術學院， 江蘇 南京 210094)

為有效提高復雜環境下的雜波抑制能力，本文提出了一種基于僅發射分集分布式超寬帶MIMO雷達體制下的波形自適應優化方法。該方法通過波束形成技術將興趣目標與雜波目標分離，并通過計算不同目標間互信息值的大小，對下一時刻的發射波形進行優選；最后根據測得目標頻域參數信息對發射信號能量進行優化分配。理論分析和仿真結果表明：在多雜波目標干擾的復雜環境下，本文方法可以獲取更多的檢測目標信息量，進而提高目標的檢測性能。

超寬帶； MIMO雷達； 波束成形； 波形設計； 信息量； 自適應； 雜波

近年來，超寬帶MIMO雷達受到了業界越來越多的關注[1-4]。超寬帶技術與MIMO雷達相結合不僅提高了雷達系統的分辨能力，同時也增加了信號的信息承載量，很大程度上提高了MIMO雷達的系統性能。因此針對超寬帶MIMO雷達的研究具有十分重要的現實意義。

目前，在復雜的雷達環境下，超寬帶雷達回波中除包含目標信息外，還存在大量雜波和干擾。由于各種障礙物的衰減作用，目標的回波信號通常較為微弱，容易被淹沒在背景雜波和噪聲中。 如果不進行有效的雜波抑制，則會對目標檢測帶來極大的困擾。因此，如何有效抑制雜波干擾是超寬帶體制下MIMO雷達所需研究的重要課題之一。對于MIMO雷達而言，由于其天線結構的特點，使得發射波形更加靈活，因此本文考慮通過優化發射波形的方法達到雜波抑制的效果。文獻[5]在噪聲環境中分別以Chernoff上限準則、互信息準則和信雜比準則推導出最優檢測MIMO波形設計，文獻[6]通過對雜波進行統計建模并對模型參數在線估計，設計了能夠最小化雜波能量的發射波形，改善了復雜場景中目標的檢測性能。文獻[7]是在雜波環境中，利用序貫假設檢驗方法進行檢測波形設計。文獻[8]分別給出了在確定性信道和隨機信道條件下對MIMO雷達波形設計，并用投影法解決了相關雜波處理問題，仿真充分證明了此方法的可行性。

上述研究在波形優化設計方面取得了優異的成果，但他們的研究都是基于窄帶MIMO雷達基礎上的。隨著發射信號帶寬的增加，目標與雜波特征都發生了改變，原有的設計方法不再能適用于當前的系統。因此，本文針對寬帶體制提出了一種自適應波形設計方法，對雜波進行了有效的抑制。

1 超寬帶MIMO雷達系統模型

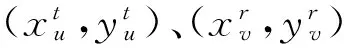
rvu(fn)=

(1)

式中：τk,v和τu,k分別代表散射中心與發射和接收端之間的時延。所以超寬帶MIMO雷達接收信號表示為

r(fn)=[r1(fn)…ru(fn)…rU(fn)]V×U

(2)

其中

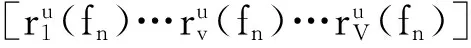
(3)

此外，考慮到超寬帶體制下信號分辨能力的提升，在復雜的雷達檢測環境中，除了興趣目標外，也檢測到許多雜波目標的存在。于是本文將興趣目標與雜波目標的信道矩陣分別表示為HT、HI。由此可以將系統模型的表示為

r=rT+rI+N=HTS+HIS+N

(4)

圖1 天線收發端與目標坐標圖Fig.1 The coordinate graph of antenna and target

2 系統架構選擇

在目標與雜波干擾并存的復雜雷達環境中，若不能有效抑制雜波干擾，雷達的檢測性能勢必要受到極大的影響。MIMO雷達天線布陣方式分為很多種，針對雜波抑制的設計需求，本文考慮采用僅發射分集的分布式陣列架構，通過這一設置，雷達系統既能滿足發射信號空間分集，以此提高對起伏目標的檢測能力，又可以在利用接收端波束形成技術有效地抑制干擾，從而提高輸出信干噪比(SINR)，改善對目標的檢測能力。

Fishler基于Neyman-Pearson準則分析了不同系統架構下的MIMO雷達的檢測性能[9]。本文將這種方法擴展到上節所提出的雷達系統模型中，并對提出模型的雷達檢測性能進行了分析與比較(為了簡化表達，下文中收發全分集分布式架構MIMO雷達簡稱為D-MIMO；僅發射分集分布式構架MIMO雷達簡稱為S-MIMO)。

全分集MIMO雷達優化檢測器表達式為

TD-MIMO=‖x‖2

(5)

式中：x代表UV×N維的匹配濾波器輸出矢量。TD-MIMO的分布形式為

(6)

同樣，對于S-MIMO而言，其優化檢測器表達式為

TS-MIMO=‖x′‖2

(7)

式中：x′代表U×N維的匹配濾波器輸出矢量。TS-MIMO的分布形式為

(8)

根據文獻[10]可以得到基于雷達檢測器信干噪比(SINR)的表達式：

(9)

情況1：當ρ=1，即信號功率與噪聲功率相同時，優化檢測器SINR可以表示為

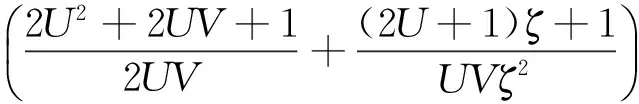
(10)

(11)

如圖2(a)所示，S-MIMO雷達的信干噪比值大于D-MIMO雷達，所以在信噪比等于1的情況下，S-MIMO的檢測性能更為優異。

圖2 不同信噪比下的優化檢測器SINR輸出Fig.2 The optimal detector SINR output for different SNR

情況2：當ρ?1, 即信號功率遠遠大于噪聲功率時，優化檢測器SINR可以表示為

(12)

(13)

由圖2(b)可以看出興趣目標信道響應方差小于雜波目標信道方差時，S-MIMO雷達的信干噪比值大于D-MIMO雷達。

情況3：當ρ?1, 即信號功率遠遠小于噪聲功率時，優化檢測器SINR可以表示為

(14)

(15)

由式(14)、(15)可以看出在這種情況下，S-MIMO雷達的檢測性能要優于D-MIMO雷達。

綜合以上可知：在多數情況下，針對存在雜波目標的復雜雷達環境，S-MIMO雷達對目標的檢測能力要優于D-MIMO雷達。所以本文的研究將基于僅發射分集的分布式MIMO雷達構架展開。

3 基于信息理論的波形自適應設計

為進一步提升對興趣目標的檢測能力，加強對雜波目標的抑制效果，本文擬從波形設計的角度出發，提出了一種基于信息理論的自適應波形優化設計方法。該方法主要分為波形優選、波形功率優化分配兩個步驟。

3.1波形優選

基于目標先驗信息，本文通過波束形成技術分別對來自興趣目標與雜波目標的回波進行加權合成，可以得到

YT=wTr=wT(HT+HI)S+N

(16)

YI=wIr=wI(HT+HI)S+N

(17)

式中：YT和YI分別表示經過波束形成后的對應目標的接收信號，wT和wI則分別表示對應的波束形成矢量。由于在每個接收端的噪聲信號均是統計獨立的，所以本文并沒有考慮波形形成對噪聲的影響。為了簡化表示，令QT=wT(HT+HI)，QI=wI(HT+HI)。接著可以用YT/I,t和YT/I,t-1表示兩個連續時刻的接收信號矢量。由式(16)、(17)可以得到

(18)

(19)

(20)

(21)

通過式(18)～(21)可以計算出RQT、RQI以及RN。由此可以估算出波形集合中的任意波形St+1∈作為發射波形后，接收端所收到的信號矢量YT/I,t+1。

根據信息論，任意兩個矢量滿足統計獨立，其互信息值達到最小。如果兩個矢量分別表示來自興趣目標與雜波目標的回波信號，則當其互信息值最小時，雷達所獲取的來自興趣目標與雜波目標的信息量就越大。換句話說，波形優選的目的在于從信號集中選取St+1使得來自興趣目標與雜波目標的互信息值達到最小。通過互信息值的計算，可以得到

I(YT,YI)=

H(YT|S)+H(YI|S)-H(YT,YI|S)

(22)

根據推導，設計的最小化互信息準則可以表示為

(23)

化處理;P0為總發射功率。

3.2波形功率優化分配

根據3.1節的優化準則，可以選出波形集合內針對當前環境最適合的發射波形，以獲得最多的興趣目標與雜波目標信息。接下來，本文針對超寬帶信號頻域豐富的特點，考慮采用頻域能量優化分配的方式，進一步提高對雜波的抑制效果。根據信息理論，可以得到關于興趣目標回波信號和接收波束之間在頻率fn處的交互信息：

In(HT(fn);r(fn)|S(fn))=

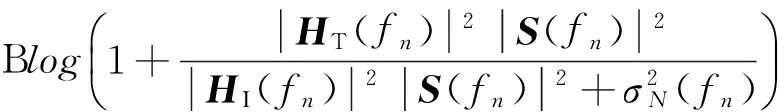
(24)

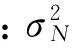
(25)

由此可以得到興趣目標與接收波束間的總互信息值。當然，不同的目標具有不同的代價函數，設計的波形不可能滿足所有目標的需求。為了解決這一問題，本文考慮多組波形聯合設計方法，組數取決于信道內存在的興趣目標數。故多組波形設計問題可以表述為

(26)

該問題的極值可以通過拉格朗日極值法進行估算。令

L(|S(f)|2,λ)=

(27)

本文設定實際發射能量滿足：

|S(f)|2≤P0/U

(28)

由式(27)、(28)可以看出信干噪比是一個隨P0增大而單調遞增的函數。因此不等式(28)可以等效為等式形式，進而得出當SINR取最大值時有：

?SINRmax/?(P0/U)>0

(29)

由于λ=?SINRmax/?(P0/U)，因此可以變相的證明拉格朗日算子為正數。所以式(30)求最大極值的問題可以轉換為

(31)

根據極值求解法可得

|S(f)|2=

(32)

根據Bell的注水理論設計原理當雜波目標回波響應幅度較大而檢測目標回波響應幅度較小時，要降低該頻率內的信號功率；而當雜波目標回波響應幅度較小而檢測目標回波響應幅度較大時，則需要加強該頻率內的信號功率。當然，對應不同的興趣目標，優化功率分布的方法也不一樣。可以根據興趣目標的數量，生成對應的自適應優化發射波形。

3.3波形設計自適應機制

依上所述，本文的自適應波形設計是一種以最優化檢測為準則的波形優選方法，其過程如下：

1)生成具有良好相關特性的發射波形，將這些波形設定為一個集合;

2)根據對接收信號連續時刻的測量，估算出RQT、RQI和RN；

4)根據得到的t時刻各個目標的頻域回波響應的大小差異，調整發射信號St+1的功率譜密度，達到抑制雜波目標，提高興趣目標檢測概率的目的；

5)將優化后的信號S′t+1作為t+1時刻的發射信號，隨后更新接收信號與目標與環境參數；

6)重復步驟2)～5)。

4 信號功率優化分配仿真

通過仿真實驗驗證上述自適應波形優化設計方法的可行性與先進性。首先，建立了一個8發8收的MIMO雷達模型，8個發射天線采用分布式布陣，而8個接收天線則采用集中式均勻線性布陣(接收陣陣元間距為λ/2)。發射信號帶寬為500 MHz，采樣頻率為2.4 GHz。為分析方便，假設檢測環境中僅存在兩個目標，興趣目標與雜波目標，分別位于接收陣元35°和45°方位。可通過波束形成技術在接收端將兩個目標的回波信號分離開來。

波形設計階段，首先采用最小化互信息準則對發射波形進行優選，如圖3所示，信息量隨著迭代次數的增多而降低，同時不同的信噪比下信息量的大小也不盡相同。信噪比越大信息量越小，降低速率也越快。這是由于隨著信噪比的增加，RQT與RQI的估計精度也在逐漸升高，導致了互信息量的降低。然后根據目標頻域響應幅度差異來優化信號能量譜密度。設定目標起伏滿足高斯模型且長度分別為30 m和20 m。假設興趣目標較大，而雜波目標較小，如圖4(a)所示，較小的目標時域響應中間高兩邊低，而較大的目標時域響應中間低兩邊高。而目標頻域響應則完全相反，如圖4(b)所示，較大的目標表現出更窄的頻域響應，即在低頻段大目標的幅值要大于小目標的幅值，高頻段則相反。從圖5可以看出，發射信號能量并不是集中在雜波功率最小的地方，而是存在于興趣目標與雜波目標功率差最大的地方。

圖3 不同信噪比下互信息最小化進程Fig.3 MI minimization process for different SNRs

圖4 不同目標時域、頻域響應Fig.4 Targets time domain response and frequency domain response

圖5 發射信號優化能量譜密度以及興趣目標與雜波雜波目標功率譜密度Fig.5 Optimal transmit ESD and interest target plus clutter target PSD

本節討論分析所提優化設計方法的自適應特性。假設虛警概率為1×10-4。從圖6可以看出隨著自適應迭代次數的增多，對興趣目標的檢測概率在不斷提升。同時也可以看出隨著迭代次數的增加，檢測概率的提升幅度也在逐步的減小，且對應值也會趨向于一個極限。最后比較了本文所提出的自適應波形優化方法采用前后的檢測概率比較圖。如圖7所示，采用該方法的檢測概率要明顯高于未采用該方法的檢測概率。

圖6 檢測概率迭代曲線圖Fig.6 Probability of target detection for various iterations

圖7 檢測概率比較圖Fig.7 Comparison of detection probability

5 結論

1) 比較了MIMO雷達不同天線架構下的雜波抑制性能。得出在雜波環境下，僅發射分集的分布式天線架構具備更優的雷達檢測能力。

2) 通過比較興趣目標與雜波的互信息值大小，選取最優發射波形，以獲得最大的目標與雜波信息。

3) 針對超寬帶信號頻域豐富的特點，通過頻域功率分配的方式可以提高興趣目標的檢測能力，有效抑制雜波干擾。

[1] SALMI J, MOLISCH A F. Propagation parameter estimation, modeling and measurements for ultra-wideband MIMO radar[J]. IEEE transactions on antennas and propagation, 2011, 59(11): 4257-4267.

[2] CHEN W J, NARAYANAN R M. CGLRT plus TDL beamforming for ultra-wideband MIMO noise radar[J]. IEEE transactions on aerospace and electronic systems, 2012, 48(3): 1858-1869.

[3] CHEN W J, NARAYANAN R M. Antenna placement for minimizing target localization error in UWB MIMO noise radar[J]. IEEE antennas and wireless propagation letters, 2011, 10: 135-138.

[4] NIJSURE Y, KADDOUM G, LEUNG H. Cognitive chaotic UWB-MIMO radar based on nonparametric bayesian technique[J]. IEEE transactions on aerospace and electronic systems, 2015, 51(3): 2360-2378.

[5] LI J, STOICA P. MIMO radar signal processing [M]. Hoboken, New Jersey: John Wiley & Sons, Inc， 2009．

[6] LI Y, MORAN W, SIRA S P, et al. Adaptive waveform design in rapidly-varying radar scenes[C]// Proc 4thinternational waveform diversity and design conference. Kissimmee, USA, 2009: 263-267.

[7] MOTI T, JOSEPH T. Waveform design for sequential detection with subspace interference[C]// IEEE sensor array and multichannel signal processing workshop, 2012: 401-404．

[8] CHEN C Y, VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]. IEEE transactions on signal processing, 2009, 57(9): 3533-3544．

[9] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE transactions on signal processing, 2006, 54(3): 823-838.

[10] SCHARF L L. Statistical signal processing: detection, estimation, and time series analysis[M]. New York: Addison-Wesley Publishing Company, 1991.

[11] LESHEM A, NAPARSTEK O, NEHORAI, et al. Information theoretic adaptive radar waveform design for multiple extended targets[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 42-55.

[12] KAY S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter reverberation[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 31-41.

[13] BELL M R. Information theory and radar waveform design[J]. IEEE transactions on information theory, 1993, 39: 1578-1597.

[14] YANG Y, BLUM R S, HE Z S, et al. MIMO radar waveform design via alternating projection[J]. IEEE transactions on signal processing, 2010, 58(3): 1440-1445.

[15] TANG B, TANG J, PENG Y. MIMO radar waveform design in colored noise based on information theory[J]. IEEE transactions on signal processing, 2010, 58(9): 4684-4697.

本文引用格式：

季晨荷，宋耀良. 針對雜波抑制的超寬帶MIMO雷達自適應波形設計[J]. 哈爾濱工程大學學報， 2017， 38(11): 1800-1805.

JI Chenhe, SONG Yaoliang. UWB MIMO radar adaptive waveform design for clutter suppression[J]. Journal of Harbin Engineering University， 2017， 38(11): 1800-1805.

UWBMIMOradaradaptivewaveformdesignforcluttersuppression

JI Chenhe, SONG Yaoliang

(School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

To improve the radar clutter rejection ability in a complex environment, this study presents an adaptive optimal waveform design method based on transmit diversity distributed ultra-wideband multi-input multi-output radar. First, the method separates the

signal from target and clutter using beam-forming technology at the receiver. Second, the waveform that is to be transmitted is selected by calculating the mutual information value between different targets. Finally, optimized energy allocation is obtained by measuring the target frequency domain parameters. Theoretical analysis and numerical results show that this method improves target detection performance by acquiring considerable amount of information about the detected target.

ultra-wideband; multiple-input multiple-output radar; beam-forming; waveform design; information; adaptive; clutter

10.11990/jheu.201606038

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1511.092.html

TN958.5

A

1006-7043(2017)11-1800-06

2016-06-14.

網絡出版日期：2017-04-27.

國家自然科學基金項目(61071145，61271331).

季晨荷(1984-), 男,博士；

宋耀良(1960-), 男, 教授,博士生導師.

季晨荷，E-mail：princekevin1984@163.com.