地震對GPS站坐標時序共模誤差的影響分析

余新平，成英燕，朱文娟，姚向東，閆忠寶

(1.山東科技大學 測繪科學與工程學院,山東 青島 266000；2.中國測繪科學研究院，北京 100830)

引用著錄：余新平，成英燕，朱文娟，等.地震對GPS站坐標時序共模誤差的影響分析[J].測繪工程，2017，26(12)：32-37.

DOI:10.19349/j.cnki.issn1006-7949.2017.12.006

地震對GPS站坐標時序共模誤差的影響分析

余新平1,2，成英燕2，朱文娟1，姚向東1,2，閆忠寶1,2

(1.山東科技大學 測繪科學與工程學院,山東 青島 266000；2.中國測繪科學研究院，北京 100830)

通過選取日本7個IGS基準站在東日本大地震前后各3 a的坐標時間序列，提取并分析此區域的共模誤差的特點和地震對其的影響，以及共模誤差對基準站噪聲時序的影響。結果表明：濾波后測站各方向坐標時序平均均方根相較于過濾前明顯減少，測站坐標可靠性和精確性得到明顯提高；地震的發生導致其N、U方向均值分別增大2.1倍和1.5倍；共模誤差在N、E、U方向均表現出明顯的周期特性，其周期特性在地震前后幾乎截然相反，地震對其周期特性的影響必須充分考慮。

IGS基準站；時間序列；共模誤差；地震；周期特性

隨著高精度的GNSS技術廣泛應用于大地測量及地震形變分析等地球動力學研究，人們對GPS位置坐標時間序列分析的研究越來越深入，尤其在噪聲特性的分析和提取方面，較大地提高了測站位置和速度估計的精度。大量研究表明，噪聲時序中除包含常見的白噪聲和有色噪聲之外，在不同GPS基準站之間還存在來源尚未明確的時空相關的共模誤差(common mode error,CME)[1-3]。共模誤差是GPS時間序列數據誤差的主要來源，它的存在會影響IGS站點坐標時間序列的分析，進而會影響其速度和誤差估計[4-7]。因此，共模誤差的提取與分析對于提高時間序列噪聲模型建立的精度至關重要。

目前對GPS坐標時序噪聲的分析絕大部分是基于連續平穩的坐標時序，但對于因地震等地質構造活動引起的非平穩坐標序列，則很少關注[8-9]。同時，對共模誤差產生機理、周期等特性和影響因素亦研究甚少。因此，本文將基于日本7個IGS基準站在2011年“3·11”東日本大地震前后各3 a的GPS坐標時序進行分析，利用區域疊加濾波方法提取出站點區域的共模誤差，并研究其周期等特性。同時，還將分析共模誤差對坐標時序以及地震對共模誤差特性的影響。

1 共模誤差分析方法

共模誤差的提取通常采用區域疊加濾波、主成分分析(PCA)和改進主成分分析法(KLE)3種空間濾波方法。殷海濤[2]等利用PCA/KLE結合的方法對四川CORS網進行共模誤差的提取，雖然其中考慮到了站點的非均勻分布及局部效應的多樣性，但所得結果精度相較于區域疊加濾波只有略微提高，且其算法較為復雜。田云峰[10]等考慮到站點間距和總體相關性水平，對區域疊加濾波進行改進，雖然對大尺度GPS網的共模誤差提取效果較好，但對于小尺度而言其殘差RMS也只改進了5%左右，且算法繁瑣。因此，本文采用算法簡單易實現的區域疊加濾波法對時空相關的共模誤差進行提取。

GPS站點坐標時間序列擬合函數模型為

y(ti)=a+bti+csin(2πti)+

dcos(2πti)+esin(4πti)+fcos(4πti)+

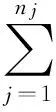
(1)

式中:ti為坐標序列日解歷元，以年為單位；a為基準站起始位置；b為線性速度；c,d和e,f分別為年周期項和半年周期項系數；gj為由于各種原因引起的階躍式坐標突變(在此處指地震引起的同震位移)；teq為地震發生時刻；H為海維西特階梯函數，地震發生前H值為0，震后H值為1；p,τ分別代表震后弛豫模型中的位移系數和弛豫時間常數；vti為坐標殘差時序。

區域疊加濾波是由Wdowinski et al.(1997)率先用于提取GPS位置坐標時序的共模誤差。Nikolaidis(2002)在計算共模誤差時加入了權重[11-12]。區域疊加濾波因其算法簡單易實現而得到廣泛應用。其基本原理可用以下模型表示：

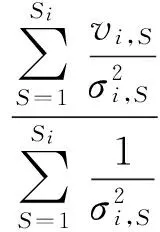
(2)

式中：ε(i)為計算的坐標時序共模誤差，vi,S為殘差坐標時間序列，σi,S為坐標單日解的中誤差，S為參與計算共模誤差的臺站數。

利用空間疊加濾波計算提取共模誤差時，首先用函數擬合坐標時間序列以去除趨勢項和周期項(對震后時序還得提取震后弛豫形變)，獲得殘差坐標時間序列; 然后以坐標單日解中誤差定權，根據式(2)提取出共模誤差; 最后提取原始時間序列中的共模誤差。

2 算例分析

2.1 共模誤差對坐標時序的影響分析

本文中所有的測站坐標時間序列都是基于日本分布較為均勻的AIRA、KGNI、MIZU、STK2、TSKB、USUD、YSSK 7個IGS站點在“3·11”東日本大地震前后各3 a的坐標時序，其站點分布如圖1所示。

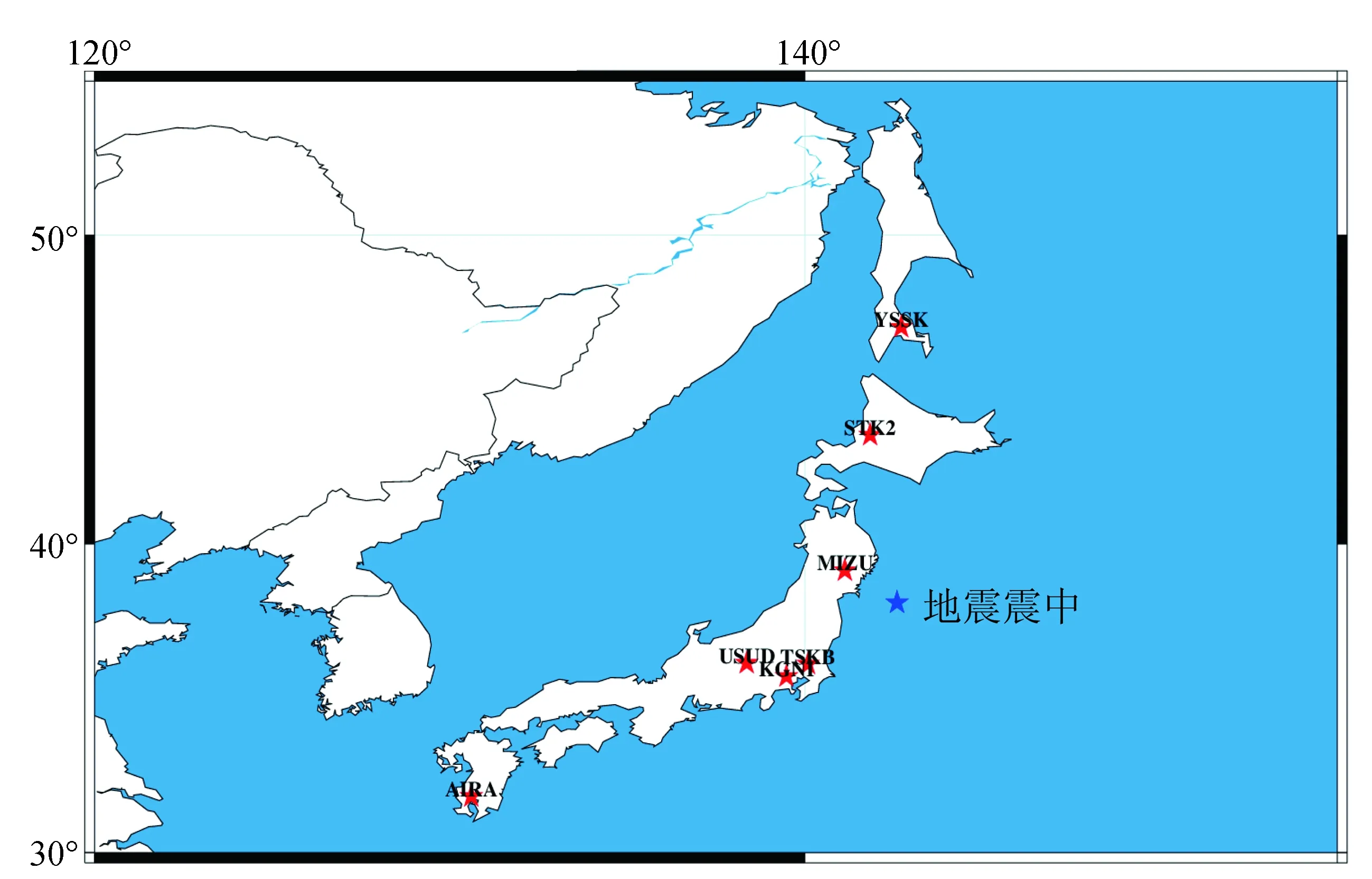
圖1 IGS站點分布圖

為了分析共模誤差的特性及其對坐標時序的影響，需要在測站原始坐標時序中完整地提取共模誤差。因此，在數據解算之前，需在震后坐標時序中按時間序列擬合函數模型剔除同震位移和呈對數形式的震后弛豫形變，以便提取較為精確的殘差時序，并依據區域疊加濾波的原理計算共模誤差的大小。在原始坐標時序中剔除共模誤差后，時序中的周期性和同震形變更加明顯，各測站的精度也均有所提高。

表1為濾波前后各站點均方根誤差，從中可以看出震后站點各方向均方根誤差隨著站點與地震震中的距離的增大而逐漸減小。在利用區域疊加濾波去除共模誤差后平均均方根誤差明顯降低，濾波前最大均方根誤差為震后MIZU的E方向，達到了23.76 cm,濾波后為11.84 cm；濾波后各站點N，E，U方向坐標時序平均均方根相較于過濾前分別減少了48%，41%，32%，震后則減小更大些，分別為57%，49%，40%。利用區域疊加濾波去除共模誤差后，IGS基準站坐標可靠性和精確性將得到明顯提高。因此，在分析測站坐標噪聲時間序列時，考慮共模誤差的影響是十分必要的。

2.2 地震對共模誤差值的影響分析

共模誤差的去除能較明顯地提高測站坐標可靠性和精確性，為了更好地了解共模誤差，下文將對共模誤差的特點及地震對其的影響進行分析。

在利用區域疊加濾波提取出共模誤差之后，可得到如圖2所示的共模誤差曲線，紅線為地震時刻。從圖中可以看出：

表1 去除共模誤差前后各站點均方根誤差 cm

1)在不同方向上，共模誤差表現出不一樣的特性,其在N、E、U方向的最大值分別為10.65 mm、9.36 mm、15.35 mm。震前共模誤差N、E、U方向均值分別為0.06 mm、0.13 mm、0.35 mm，而震后各方向均值皆有所增大，U方向增加近1.5倍，為0.82 mm；其次為N方向的0.19 mm，增加了2倍多，變化最小的為E方向的0.15 mm，與震前基本相近。

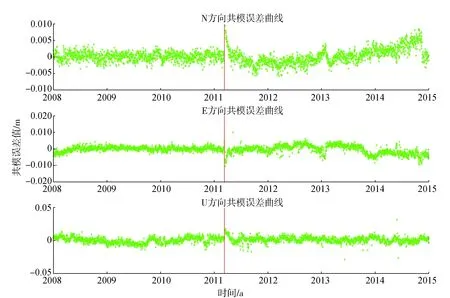
圖2 N、E、U方向共模誤差曲線(紅線表示地震時刻)

2)地震發生后，共模誤差在各方向表現出與震后弛豫形變相似的變化規律，這其中可能含有未被完全剔除的震后弛豫形變的影響。

雖然共模誤差的來源尚不明確，但利用區域疊加濾波的方法能較好地將其剔除。當發生地震時，地震對共模誤差的影響也應充分考慮，以提高IGS基準站坐標的精度。

2.3 地震對共模誤差周期特性的影響

為了更加直觀地反映地震對共模誤差的影響以及共模誤差周期特性的變化，下面通過對共模誤差各方向坐標進行功率譜估計，并繪制其周期功率譜圖。

圖3、圖4中的紅線表示地震前后共模誤差的擬合曲線，從中可以看出，共模誤差的周期特性在各方向上均有差異，N、U方向表現出明顯的短周期特性，而E方向在震后則表現出非常明顯的年周期特性，且周期振幅增大明顯。

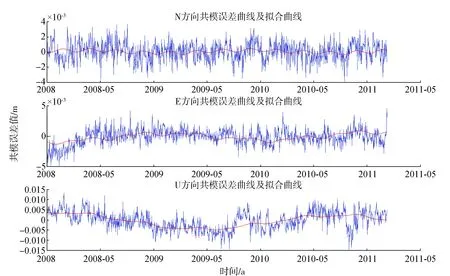
圖3 震前共模誤差曲線及其擬合曲線(紅線)

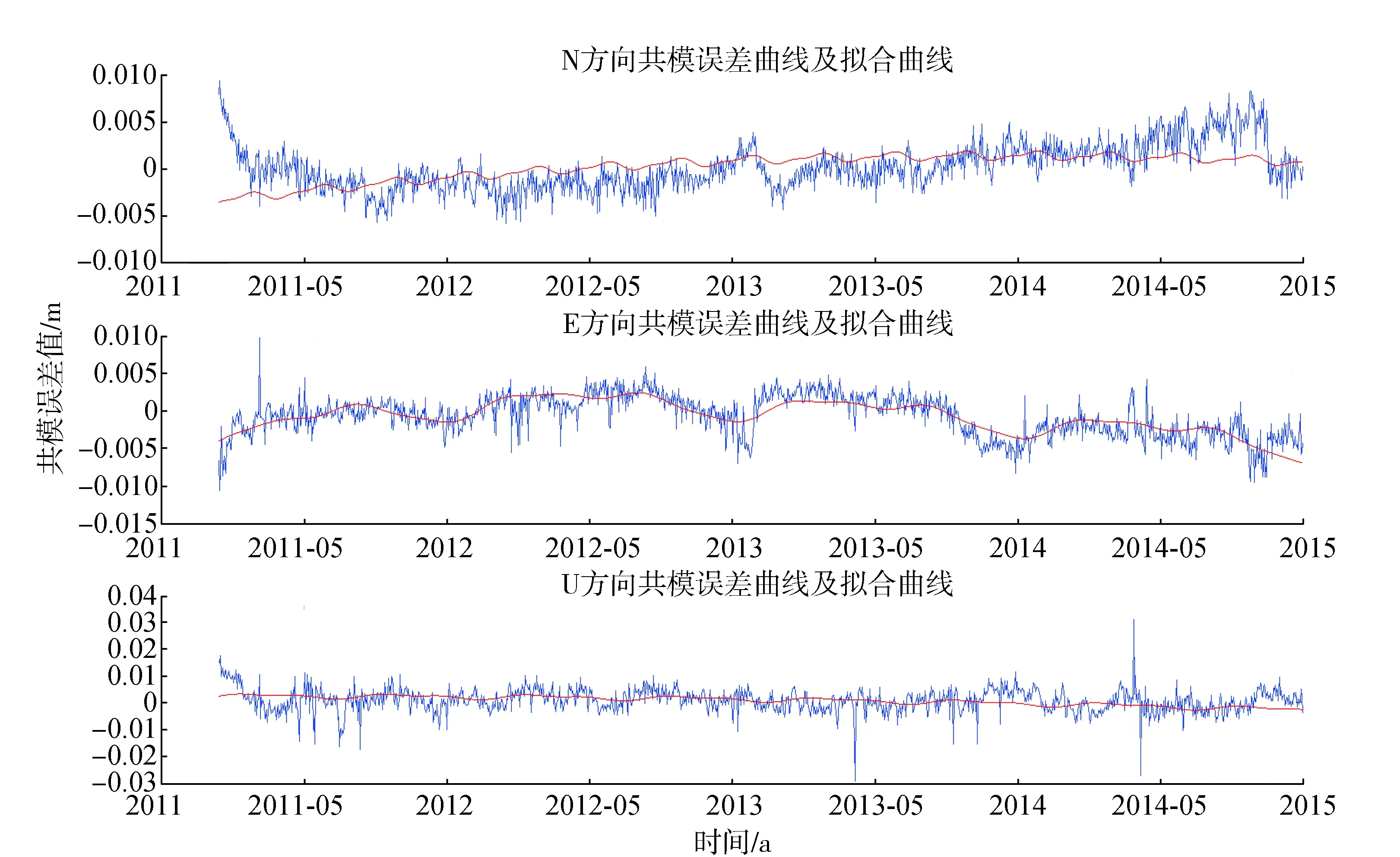
圖4 震后共模誤差曲線及其擬合曲線(紅線)

與共模誤差各方向對應，在去除震后弛豫形變后對其進行功率譜估計。如圖5、圖6所示為地震前后各向共模誤差的功率譜周期圖，從中可以看出：震前共模誤差在NEU方向表現出明顯的1.25 a周期，約半年的周期功率較小；E方向約半年和1.5 a周期明顯；相較于N、E方向的長周期，U方向周期則表現為約一個季度，1.5 a周期不是很明顯。震后共模誤差的周期特性與震前幾乎截然相反，相較于震前N、E方向的長周期，震后其均表現出明顯的季度周期，E方向還表現出較明顯的年周期；震前表現明顯季度周期的U方向，在震后卻變為1 a和2 a的長周期。

從以上對共模誤差的分析可知其具有很明顯的周期特性，這種與時間有關的公共誤差與共模誤差的定義是相符的[3,13]。雖然共模誤差產生機理及影響因素尚不明確，但通過分析地震等地質構造活動因素的影響可知，地震對共模誤差尤其對其周期特性的影響很大，因此，在噪聲時序分析和共模誤差提取及分析時，均要考慮到地震因素的影響。

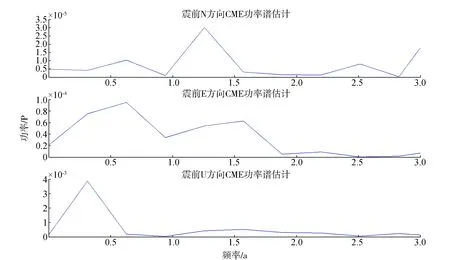
圖5 震前共模誤差曲線功率譜估計

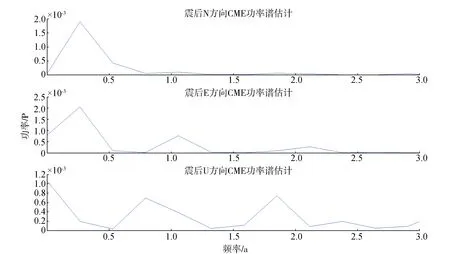
圖6 震后共模誤差曲線功率譜估計

3 結 論

本文采用空間疊加濾波法對日本區域7個IGS基準站區域間的共模誤差進行提取和分析，所得結果表明：

1)共模誤差的剔除較大的降低了大尺度因素對IGS基準站測站坐標時間序列的影響，濾波后測站各方向坐標時序平均均方根相較于過濾前分別減少了48%，41%，32%，震后減小更大，測站坐標可靠性和精確性將得到較明顯提高。

2)地震的發生使得共模誤差各方向均值皆增大，N、U方向增加明顯，分別增加近1.5倍、2倍，E方向均值與震前基本相近。

3)地震對共模誤差的周期特性影響明顯，震后共模誤差的周期與震前幾乎截然相反，且震后除U方向外，水平方向季度周期表現明顯。因此，地震對共模誤差的影響不容忽視，必須考慮。

本文雖對共模誤差的來源和影響因素進行了有益的探索，但在共模誤差提取時未充分考慮區域中站點間的距離以及所選取的基準站坐標時間序列的長度，后續將做進一步研究分析。

[1] 伍吉倉，孫亞峰，劉朝功．連續GPS站坐標時間序列共性誤差的提取與形變分析[J]．大地測量與地球動力學,2008,28(4):97-101.

[2] 殷海濤,甘衛軍, 熊永良,等.PCA空間濾波在高頻GPS定位中的應用研究[J].武漢大學學報(信息科學版),2011,36(7):825-829.

[3] 呂成亮,張勝凱,沈飛,等.基于共性誤差的CORS站坐標時間序列分析[J].大地測量與地球動力學，2016, 36(1):16-20.

[4] 黃立人.GPS 基準站時間序列的噪聲特性分析[J].大地測量與地球動力學，2006，26(2): 31-33.

[5] LANGBEIN J.Noise in GPS displacement measurements from Southern California and Southern Nevada[J].Journal of Geophysical Research,2008,113(B5):1-12.

[6] 蔣志浩，張鵬，秘金鐘，等．顧及有色噪聲影響的CGCS2000下我國CORS站速度估計[J]. 測繪學報，2010，39(4):355-363.

[7] 李昭，姜衛平，劉鴻飛，等.中國區域IGS基準站坐標時間序列噪聲模型建立與分析[J].測繪學報，2012,41(4):496-503.

[8] 楊國華，張風霜，武艷強，等.GPS基準站坐標分量噪聲的時間序列與分類特征[J].國際地震動態,2007(7):81-85.

[9] 廖華，徐銳，陳維鋒，等.汶川地震前后四川區域GPS時序特征演變及統計分析[J].地球物理學報，2013,56(4):1237-1245.

[10] 田云鋒,沈正康. GPS觀測網絡中共模分量的相關加權疊加濾波[J].地震學報,2011，33(2): 198-208.

[11] 田云鋒,沈正康.GPS坐標時間序列中非構造噪聲的剔除方法研究進展[J].地震學報, 2009,31(1):68-81.

[12] WILLIAMS S D P．Error analysis of continuous GPS position time series[J]．Journal of Geophysical Research，2004，109(B3):412-430.

[13] 蘇利娜,丁曉光,張彥芬,等.陜西連續 GPS 基準站坐標時間序列分析[J].大地測量與地球動力學，2014,34(5):106-113.

[責任編輯：劉文霞]

InfluenceofearthquakeonthecommonmodeerrorofGPSstationcoordinatetimeseries

YU Xinping1,2,CHENG Yingyan2,ZHU Wenjuan1,YAO Xiangdong1,2,YAN Zhongbao1,2

(1.School of Geomatics，Shandong University of Science and Technology，Qingdao 266000,China；2.Chinese Academy of Surveying and Mapping,Beijing 100830,China)

Focused on the coordinate time series captured from 7 IGS reference stations in three years before and after the March 11th Japan earthquake, the common mode error of this region is extracted, and meanwhile, the characteristics of the common mode errors, the influence of the earthquake and the influence of common mode error on the noise time series of reference station in this area are analyzed.Conclusion are drawn that after filtering, the mean RMSE of the coordinate time series in each direction is obviously reduced, and the reliability and accuracy of the measuring station coordinate are obviously improved.The occurrence of earthquake leads to the increase of N and U direction respectively 2.1 times and 1.5 times.The common mode errors in N, E, U direction all show a relatively obvious periodic characteristic, and the period characteristic of the common mode is quite different from before and after the earthquake. Thus,the influence of the earthquake on the period characteristic must be fully considered.

IGS reference station; time series; common mode error; earthquake;periodic characteristics

P228.4

A

1006-7949(2017)12-0032-06

2016-10-20

國家重點研發計劃資助項目(2016YFB0501405);國家自然科學基金資助項目(41374014)；國家公益性行業專項資助項目

余新平(1992-)，男，碩士研究生.