改進的ANFIS模型在河道堤防物理力學參數反演計算中的應用

齊 奇

改進的ANFIS模型在河道堤防物理力學參數反演計算中的應用

齊 奇

（遼寧省江河流域管理局，遼寧 沈陽 110003）

文章結合自適應函數對傳統ANFIS模型進行改進，并將改進的ANFIS模型對遼寧西部某中小河流河道堤防的物理力學參數進行反演計算，并結合正交試驗確定模型計算的訓練樣本，確定改進的ANFIS模型巖石力學參數反演的映射結構，同時結合河道堤防原位監測的位移數據，對改進前后的模型參數反演誤差進行了對比分析。結果表明，改進的ANFIS模型可提高河道堤防參數反演精度，相比于傳統模型，改進模型的參數反演計算堤頂下降以及周邊位移和監測位移之間的誤差分別減少14.8%和18.6%。研究成果可在河道堤防參數設計中進行推廣和應用。

自適應函數；改進的ANFIS模型；河道堤防物理力學參數反演；反演精度分析

河道堤防穩定性分析和設計需要對堤防物理力學參數進行確定，而對這些力學參數進行準確評估，可提高河道堤防設計的合理性和穩定性，從而確保河道堤防的工程安全。早期，對于河道堤防物理力學參數的確定主要通過原型試驗方式進行試驗測定［1-3］，但是這種方法需要大量的人力和物力，且由于采樣的天然巖石存在較多的裂隙，使得試驗測定參數結構和實際結構存在較大的誤差。當前，結合試驗測定的數據，結合參數反演的計算方法為合理確定河道堤防物理力學參數提供了較為有效的途徑［4-6］。這其中傳統的ANFIS模型在樣本訓練計算具有唯一性，且收斂速度較快的特點，近些年來，在許多工程設計中的參數反演得到應用［7-8］，但是傳統 ANFIS模型在計算中未能實現參數的優化計算，使得模型計算收斂精度有所欠缺，為此有學者引入自適應函數［9］對傳統ANFIS模型進行優化和改進，提高模型收斂精度。為分析改進的ANFIS模型在河道堤防物理力學參數反演中的適用性，本文引入改進的模型，以遼寧西部某中小河流河道堤防物理力學參數進行反演，并結合監測數據，對比改進前后模型的反演計算精度。

1 ANFIS模型河道巖石力學參數反演原理

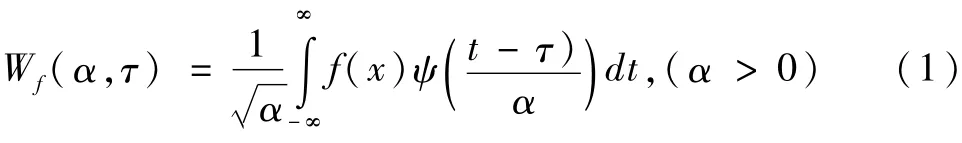
式中，τ—橫向水平狀態變量值；α—小波變換函數縱向狀態變量值，t—小波神經網絡模型計算步長。

在采用小波變換函數進行轉換求解后，采用小波分析方法對函數進行分析，分析方程為：

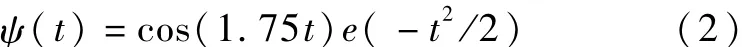
ANFIS模型結合控制方程對模型進行節點計算，各節點控制方程為：

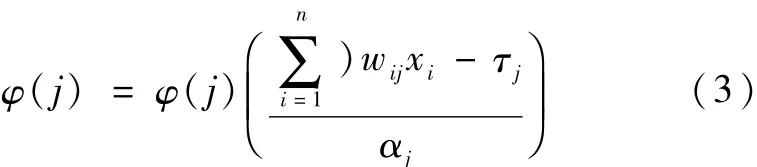
式中，φ（j）—小波神經網絡模型隱含層節點控制值；αj—模型計算基礎函數；i—小波神經網絡模型隱含層節點控制個數；wij—不同狀態變量的權重取值；τj—隱含層節點數j時間步長。

在確定模型計算權重后，可以得到小波神經網絡模型的目標計算值，計算方程為：

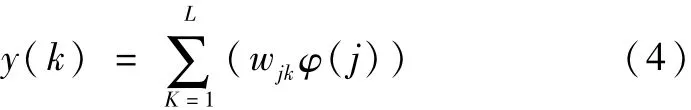
式中，k—計算變量的個數。

在傳統模型計算基礎上，改進的ANFIS模型采用自適應函數對模型樣本數據訓練計算進行優化，其中優化的目標函數為：

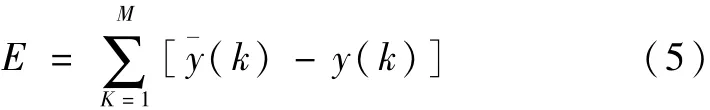
式中，ˉy（k）—訓練計算樣本數值；y（k）—采用改進的ANFIS模型反演計算值；m—訓練樣本的個數，結合自適應函數，模型引入效率系數η對傳統模型橫向和縱向的控制參數進行優化，各參數優化表達式為：

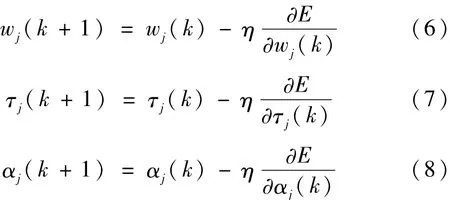
式中，E—自適應函數目標值；其他變量同方程（1）、 （2）、 （3）中所述的變量含義。

2 實例應用

2.1 河道堤防工程概況

本文以遼寧西部某種小河流為實例，該河道堤防長度為4.0km，河堤底部的高程為3.0～5.0m，整個河道堤防的寬度為45m，現狀河道堤頂高程為13.5m，河道堤防迎水坡比大部分地段約1∶3，局部較陡處約1∶2.5。河道堤防地層主要為太古界混合巖、古生界大理巖、中生界白堊系安山巖、礫巖及新生界第四系松散堆積層。為分析改進模型在河道堤防巖石力學參數反演計算的適用性，對河道堤防進行了位移和力學參數的觀測試驗，堤防位移監測點和監測數據見圖1和表1。

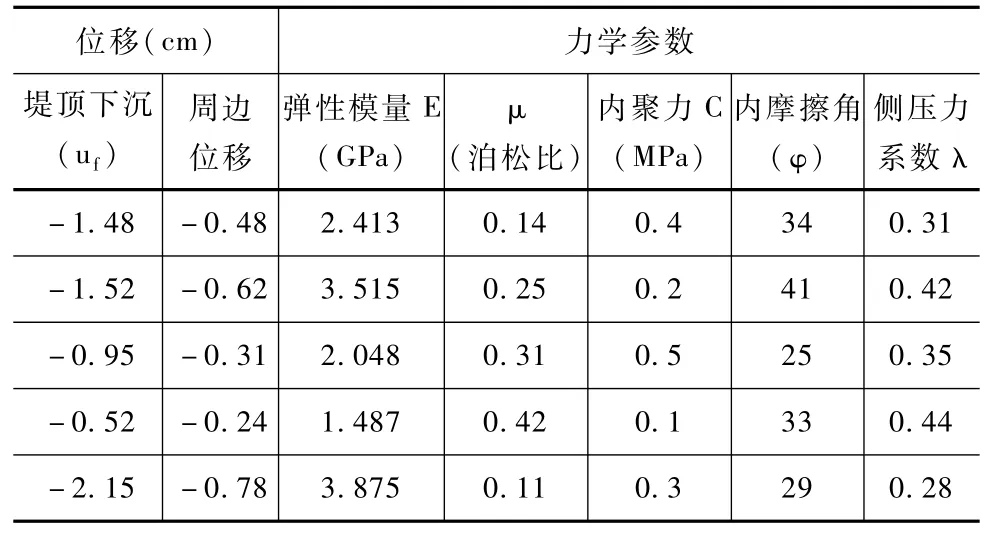
表1 河道堤防原型觀測數據

2.2 模型反演參數及取值范圍的確定

在模型參數反演計算前，對模型主要的力學參數進行了取值范圍的確定，各參數的取值范圍間表2。

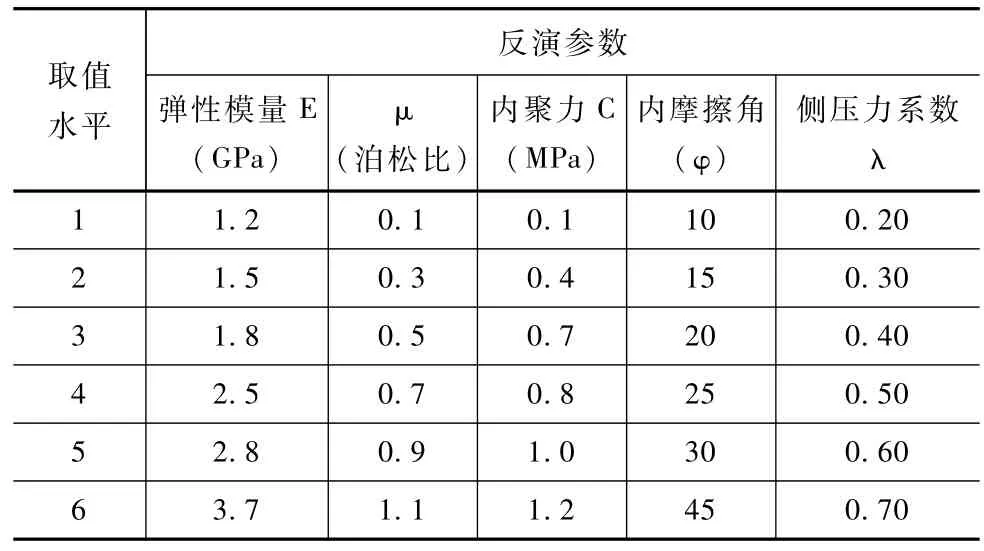
表2 ANFIS模型參數取值范圍

從表中可以看出在取值水平1～6下，河道堤防巖石彈性模量參數的變化范圍為1.2～3.7GPa，泊松比的變化范圍為0.1～1.1之間，內聚力C的取值范圍在0.1～1.2GPa，對于河道堤防穩定較為重要的內摩擦角的取值范圍為10～45之間，對于側向穩定性較為重要的側壓力系數的取值范圍為0.20～0.70之間。

2.3 基于ANFIS模型的參數反演計算

2.3.1 河道堤防物理力學反演參數和邊坡位移映射關系

圖1 河道堤防位移監測示意圖

為對模型的收斂度進行分析，采用正交試驗的方式確定不同計算方案下的堤頂下沉和周邊位移量，分析結果見表3。并結合20組正交試驗數據，對改進的ANFIS模型進行了訓練，統計不同演算次數下的訓練誤差分布，結果見圖2。

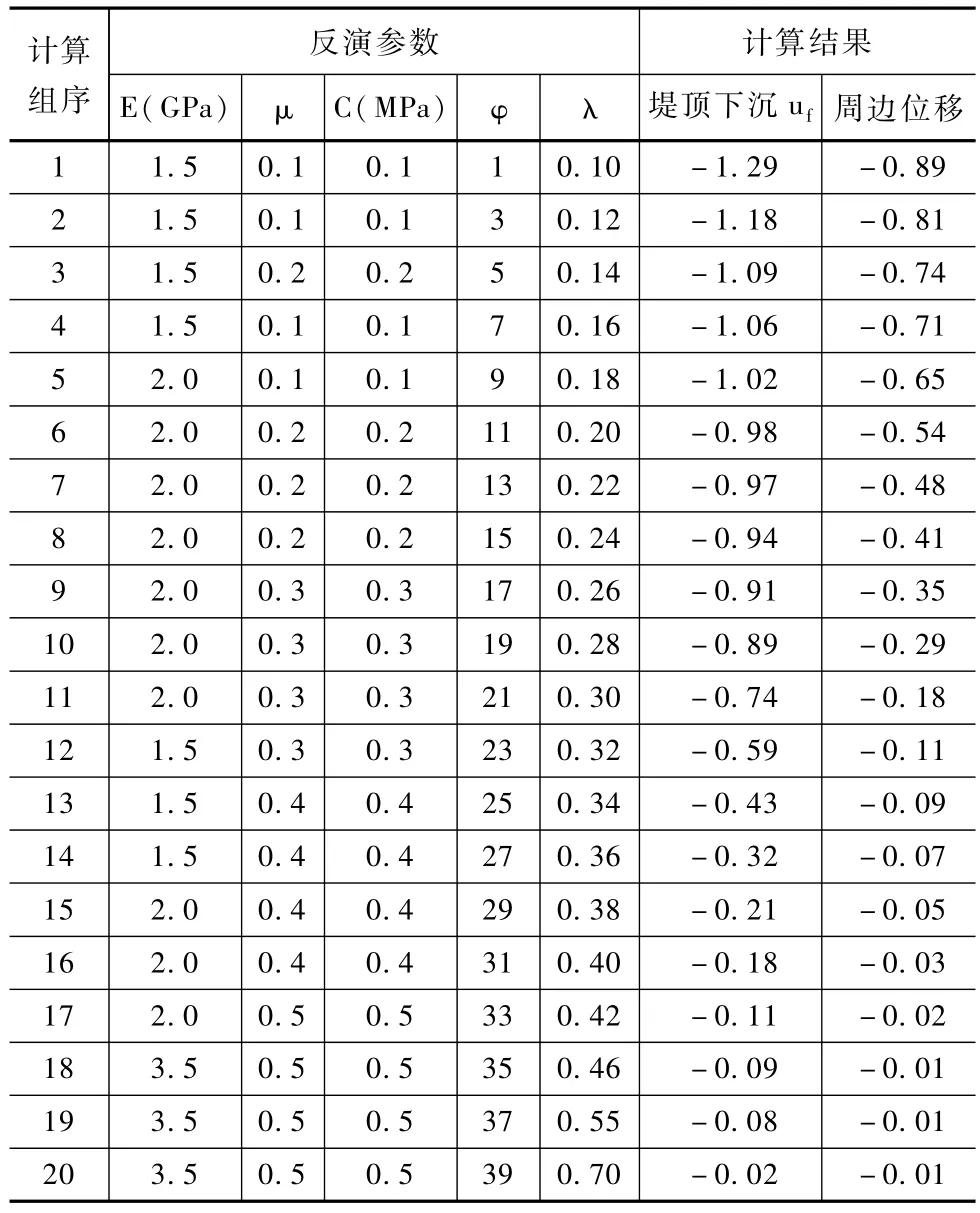
表3 不同計算方案下的參數反演計算結果

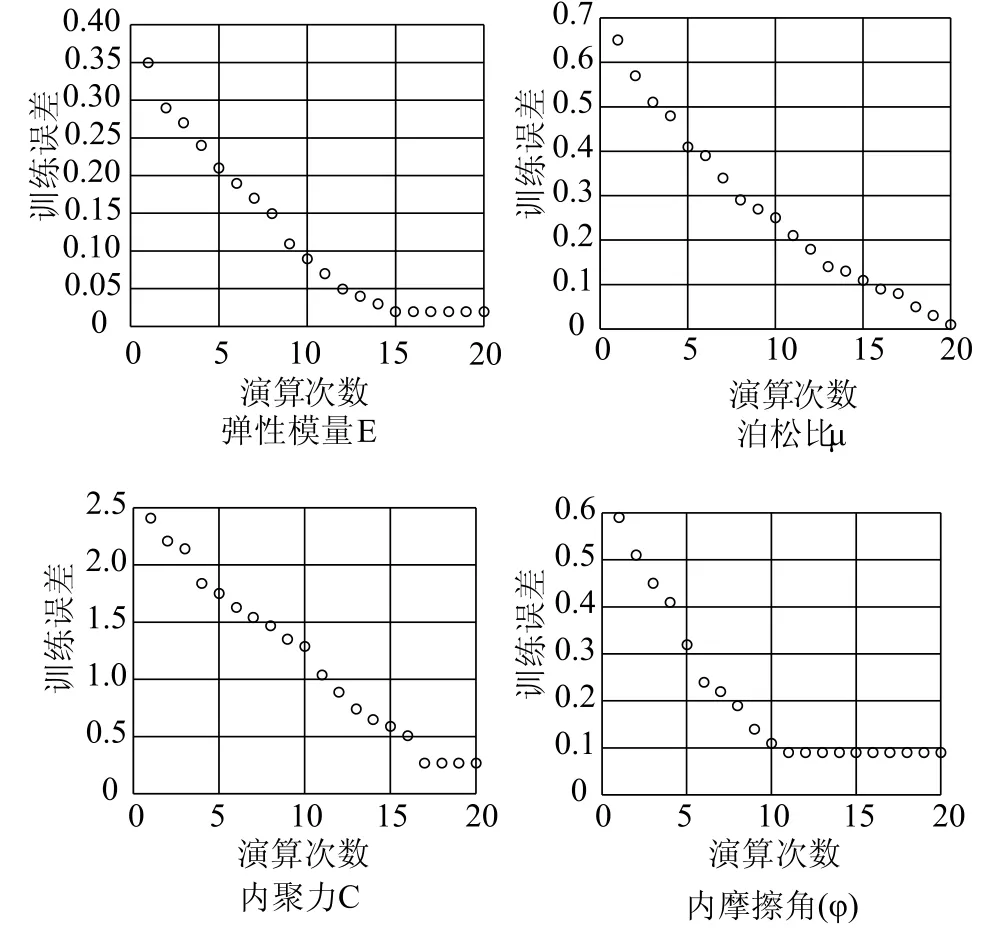
圖2 各力學參數反演計算誤差分布

表3為不同計算方案下的參數反演計算結果，從表中可以看出，當組序從1增加到20后，計算的壩頂沉降值從-1.29cm減少到-0.02cm，其堤防邊坡位移從-0.89cm減少到-0.01cm，隨著組序的增加，其壩頂沉降和周邊位移也逐漸遞減。從圖2中可以看出，各參數的力學參數反演計算訓練誤差分布變化規律較為相近，在演算初期，其誤差均較大，隨著訓練次數的增加，由于加入自適應函數對模型訓練演算進行優化，使得各個參數的收斂速度均有所加快，各參數反演訓練誤差的分布曲線均較陡，從圖中可以看出，各個參數反演訓練次數達到20次時，各參數基本達到最優結果。

2.3.2 基于改進的ANFIS模型的參數反演結果

在模型訓練基礎上，采用改進的ANFIS模型對河道進行了5組參數反演計算，計算結果見表4。

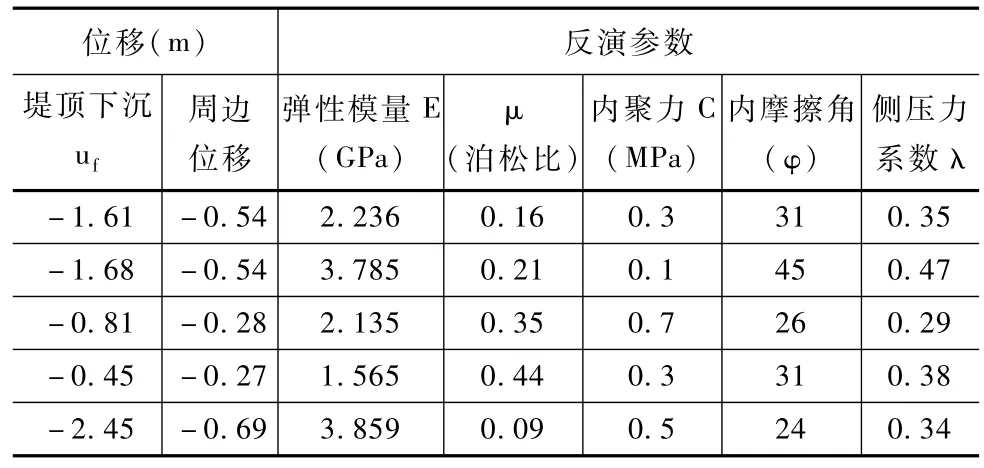
表4 基于改進的ANFIS模型河道堤防力學參數反演結果

2.3.3 改進前后模型的巖石力學參數反演誤差評定結果

為對比分析改進前后的ANFIS模型在河道堤防巖石力學參數反演的精度，結合原型觀測試驗的數據，對改進前后模型反演計算的位移量進行了誤差評定，評定結果見表5和表6。

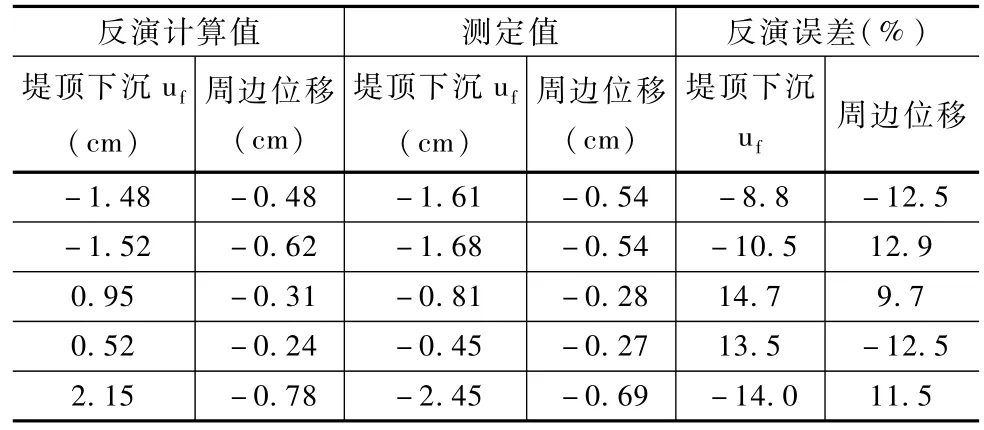
表5 改進模型誤差評定結果

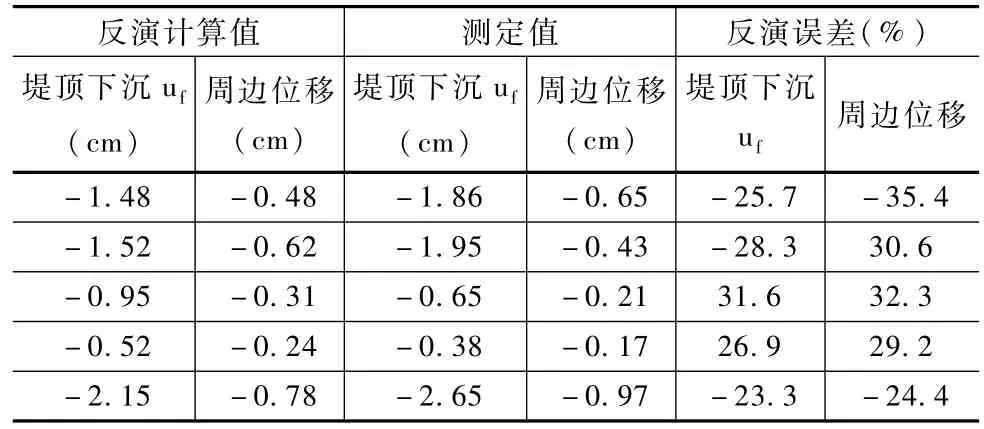
表6 傳統模型誤差評定結果

從表5中可以看出，在5組監測數據中，改進的ANFIS模型在河道堤防物理力學參數反演計算的堤頂下沉量和監測下沉量之間的誤差在-8.8%～-14.0%之間，周邊位移之間的誤差在9.7%～12.9%之間，各誤差均在20%以內。從表6中可以看出，傳統ANFIS模型在河道堤防物理力學參數反演計算的堤頂下沉量和監測下沉量之間的誤差-23.3%～31.6%之間，周邊位移之間的誤差在-24.4%～-35.4%之間，各誤差均大于20%，相比于傳統模型，改進模型的參數反演計算堤頂下降以及周邊位移和監測位移之間的誤差分別減少14.8%和18.6%。可見，改進的ANFIS模型在河道堤防物理力學參數反演精度好于傳統模型，反演精度得到明顯改善。

3 結語

本文結合改進的ANFIS模型對河道堤防物理力學參數進行反演計算，并結合遼寧西部某中小河流河道堤防位移和參數測定數據對模型反演精度進行了誤差評定，結果表明相比于傳統的ANFIS模型，改進模型在物理力學參數反演精度上得到明顯改善，為河道堤防工程設計參數確定提供了一種有效的技術手段。

［1］李曉龍.基于支持向量機的巖體力學參數反演及工程應用［D］.鄭州大學，2009.

［2］李波，徐寶松，武金坤，等.基于最小二乘支持向量機的大壩力學參數反演［J］.巖土工程學報，2008（11）：1722-1725.

［3］習紅凱，馬福恒，劉成棟.某碾壓混凝土重力壩物理力學參數反演分析［J］.水利規劃與設計，2009（02）：45-47.

［4］江小輝，吳文峰.大橋樁基工程對河道堤防邊坡變形的影響分析［J］.水利規劃與設計，2007（05）：43-45.

［5］王強社，任園園.安康市濱江大道堤防工程工程地質條件及評價［J］.陜西地質，2014（01）：77-81.

［6］向衍，鄭東健，何旭升，等.基于MSC.Marc的物理力學參數反演［J］.水電能源科學，2003（04）：7-10.

［7］王永秀，毛德兵，齊慶新.數值模擬中煤巖層物理力學參數確定的研究［J］.煤炭學報，2003（06）：593-597.

［8］張志軍，丁德馨，畢忠偉，等.位移反分析的ANN方法與ANFIS方法的比較分析［J］.采礦與安全工程學報，2008（02）：159-163.

［9］馬細霞，胡鐵成.基于ANFIS的水庫年徑流預報［J］.水力發電學報，2008（05）：33-36+22.

TP391.41

B

1008-1305（2017）05-0144-04

10.3969/j.issn.1008-1305.2017.05.044

2017-04-06

齊 奇（1988年—），女，工程師。