沙棘果實-果柄系統振動采收機理分析與仿真

彭 俊，孫世鵬，馮亞利，楊有剛,傅隆生

(西北農林科技大學 機械與電子工程學院，陜西 楊凌 712100)

?

沙棘果實-果柄系統振動采收機理分析與仿真

彭 俊，孫世鵬，馮亞利，楊有剛,傅隆生

(西北農林科技大學 機械與電子工程學院，陜西 楊凌 712100)

沙棘在西部廣泛種植，用于水土保持和防風固沙。其果實營養豐富、有較高經濟價值，但采收非常困難，影響其經濟價值。為改變人工采摘的狀況，有必要進行沙棘的機械化采收研究。為此，研究了沙棘果實與果柄脫離的振動采摘機理，建立了雙自由度受迫振動物理模型，推導出動力學方程，并采用數理微分方程求解得到沙棘果實-果柄系統穩態受迫振動輸出解及采摘慣性力。同時，通過貝塞爾函數曲線模擬果實的幾何形狀，得出果實幾何輪廓曲線方程，并利用Pro/E的函數功能畫出沙棘果實的三維模型，將模型導入有限元分析軟件ANSYS進行了模態分析。結果表明：理論計算的果實-果柄系統的位移、速度和加速度響應與有限元仿真分析的結果比較相符，頻率在18～46Hz范圍內時，果實部分產生共振且主振型最大，故果實的最佳采摘頻率范圍可確定為18～46Hz。該研究為沙棘振動采摘裝備的開發提供理論基礎。

果實-果柄；振動采收；有限元方法；模態分析

0 引言

沙棘(sea buckthorn)屬胡頹子沙棘屬，為落葉灌木，其果實為漿果。沙棘是優良的水土保持樹種，因此在中國西部被廣泛的種植，面積約為266.7hm2，占到世界沙棘資源儲量的95%以上。沙棘果實富含維生素和酚類化合物，在世界上的某些地區作為藥材和食品[1-2]；但沙棘果小、柄短，且樹枝有刺，難以采收。在加拿大，收獲4hm2的沙棘所需的勞動力成本占生產總成本的58%。在亞洲，收獲仍主要依靠手工或使用簡單的手持工具，需要大約1 500工時/hm2[3]。因此，機械或其他沙棘果實收獲技術的發展已經引起了相當大的關注。

果樹的機械特性隨著樹種、品種和樹的幾何結構的變化而差異很大，但果實-果柄結構的機械特性變化不是很明顯[4]，故本文將沙棘果實-果柄作為沙棘樹的一個基礎系統來研究其振動采摘機理，為沙棘的機械振動采收提供一定的理論基礎。

1 沙棘果實果柄系統振動機理研究

1.1 果樹系統建模

為了解果樹結構在振動激勵下的動態響應，Savary等建立了柑橘的主干側枝有限元模型，分析了模型在沖擊激勵下的加速度值。其仿真結果與實驗結果比較吻合，兩種方法得出的數據都表明了同一結論：激振頻率越高，果樹的加速度越大[5]。Láng建立了基于樹干-主根的單自由度結構模型，研究表明：當振動位置靠近根部時，旋轉式偏心振子激振器更有效，而激勵作用點靠近樹枝時，曲柄滑塊式激振器更有效[6]。Upadhyaya等將樹葉和樹干上的小枝忽略，把主干分成許多個近似均勻的單元，采用Timoshenko梁理論進行計算，所得結果與測試結果比較接近[7]。Yung和Fridley將果樹簡化為由樹干-樹枝、樹枝-樹葉、果實-果柄3種具有不同力學特性的單元構成，并利用有限元方法分別對3種單元體的動力學模型進行了模擬，模擬分析結果與計算結果一致[8]。

1.2 果實-果柄系統采摘條件及受力模型建立

在振動過程中，當振動使果實產生的慣性力大于果實-果柄的連結力時，果實才能脫離下來。因此，可以將果實-果柄結構作為樹的一個基礎系統來研究，以確定最佳的振動頻率和收獲成熟果實的效率。當振動激勵作用于樹枝時，樹枝和果實做強迫振動，振動響應X(t)為瞬態響應和穩態響應之和，即

X(t)=xT(t)+xS(t)

(1)

其中，xT(t)為沙棘樹枝果實的瞬態響應；xS(t)為沙棘樹枝果實的穩態響應。

由式(1)得受迫振動沙棘果實所受慣性力F(t)為

(2)

其中，m2為沙棘果實的質量。由于瞬態振動xT(t)是衰減振動，只在振動開始的很短時間內才有效，一般情況都不考慮[10]，主要研究輸出穩態響應xS(t)下的慣性力。若果實與樹枝的連結力為F0，則實現振動采摘的條件為：振動產生的慣性力F(t)≥F0。以果實和樹枝為研究對象，建立沙棘樹枝果實的幾何模型與力學模型，求解振動采摘過程中果實的動態響應，如圖1所示。

(a)

(b)

1.3 果實-果柄系統振動物理模型建立與求解

當沙棘樹枝受到采摘激振力Fsinωt時，樹枝整體會產生振動響應，沿樹枝方向每個單位長度的樹枝在振動響應下都會產生慣性力F(t)。沙棘的果柄很短，直徑也很小，故其質量相對于樹枝和果實的質量可以忽略不計。根據振動理論，可以將樹枝果實系統看作二自由度的彈簧質量塊振動系統，如圖2所示。系統振動微分方程為

(K1+K2)x1-K2x2=Fsinωt

(3)

(4)

其中，x1、x2分別為樹枝的位移和果實的位移；K1、K2分別是樹枝和果柄的等效剛度。

樹枝振動時，可將其看作是與主干連接處為固定端的懸臂梁，當受到外力時發生彎曲變形，樹枝彎曲等效剛度K1，果柄可以近似為圓柱體，其等效拉伸剛度K2，則有

K1=3EJ/L13，K2=EA/L2

(5)

其中，E為材料彈性模量；J為截面慣性矩；L1為樹枝長度；A為果柄截面積；L2為果柄長度。

其受迫振動的位移響應為

x1=A1ei(ωt-φ)，x2=A2ei(ωt-φ)

(6)

其中，A1、A2分別為樹枝的位移和果實的位移的振幅。將式(6)代入得

(7)

Δ=[K1K2+

(m1m2ω4-r1r2ω2-K1m2ω2-K2m1ω2-K2m2ω2)]2+

(K1r2ω-m2r1ω3-m2r2ω3-m1r2ω3+K2r1ω)2

(8)

由于系統的阻尼對系統固有頻率的影響很小，故系統的固有頻率可表示為

(9)

2 果實果柄系統有限元分析

2.1 果實樹枝物理參數測定

J. Khazaei等[11]研究了不同溫度和載荷對沙棘果實的機械特性及應力松弛的影響。對漿果進行了穿刺實驗，對不同溫度下的大果沙棘的密度、彈性模量及泊松比進行了測試。樹枝樣本取材于新疆青河縣大果沙棘良種基地，密度用排水法測量。

尚大軍等對沙棘木材的力學性能進行了測定，實驗結果表明：應力波測得未經處理的中國沙棘木材彈性模量與超聲波測得結果相差不大[12]。張厚江等用兩點懸掛振動測定了木材的動態彈性模量[13]。劉鎮波等采用基于打擊音的快速傅里葉變換(FFT)頻譜分析法測量了木材彈性模量[14]。賀磊盈在研究山核桃樹枝干的結構參數時，采用了懸臂梁振動實驗測得樹枝的動態彈性模量[15]。動態彈性模量為

(10)

由于木材粘彈性的存在，振動過程中不可避免地存在阻力，因而在一定時間內振動會逐漸衰減而停止。阻尼的種類很多，通常都以粘性阻尼為基本模型來分析有阻尼的振動，對于非粘性阻尼可以引進等效粘性阻尼來近似計算[16-17]。陳守謙用衰減振動法對木材的阻尼比進行了測定，通過測得木材自由衰減振動的對數衰減率δ，再通過阻尼比ζ與δ的關系求出阻尼比[18-19]。阻尼比ζ與對數衰減率δ的關系式為

(11)

其中，A1和A1+N分別表示振動信號的第1個波峰幅值和第1+N個波峰幅值。

采用懸臂梁振動實驗，實驗材料包括：沙棘樹枝，固定樹枝的虎鉗，施加激勵的激振錘(京儀北方測振儀器分公司，LC-1)，加速度計(KYOWA公司的AS-2GB)。將樹枝加工成圓柱形，用虎鉗夾住一端并安裝加速度計，另一端用激振錘敲擊，記錄樹枝振動的加速度。對振動加速度信號進行快速傅里葉變換(FFT)，提取1階共振頻率信號，如圖2所示。實驗測得樹枝具體參數如表1所示。

(a) 振動加速度時域響應

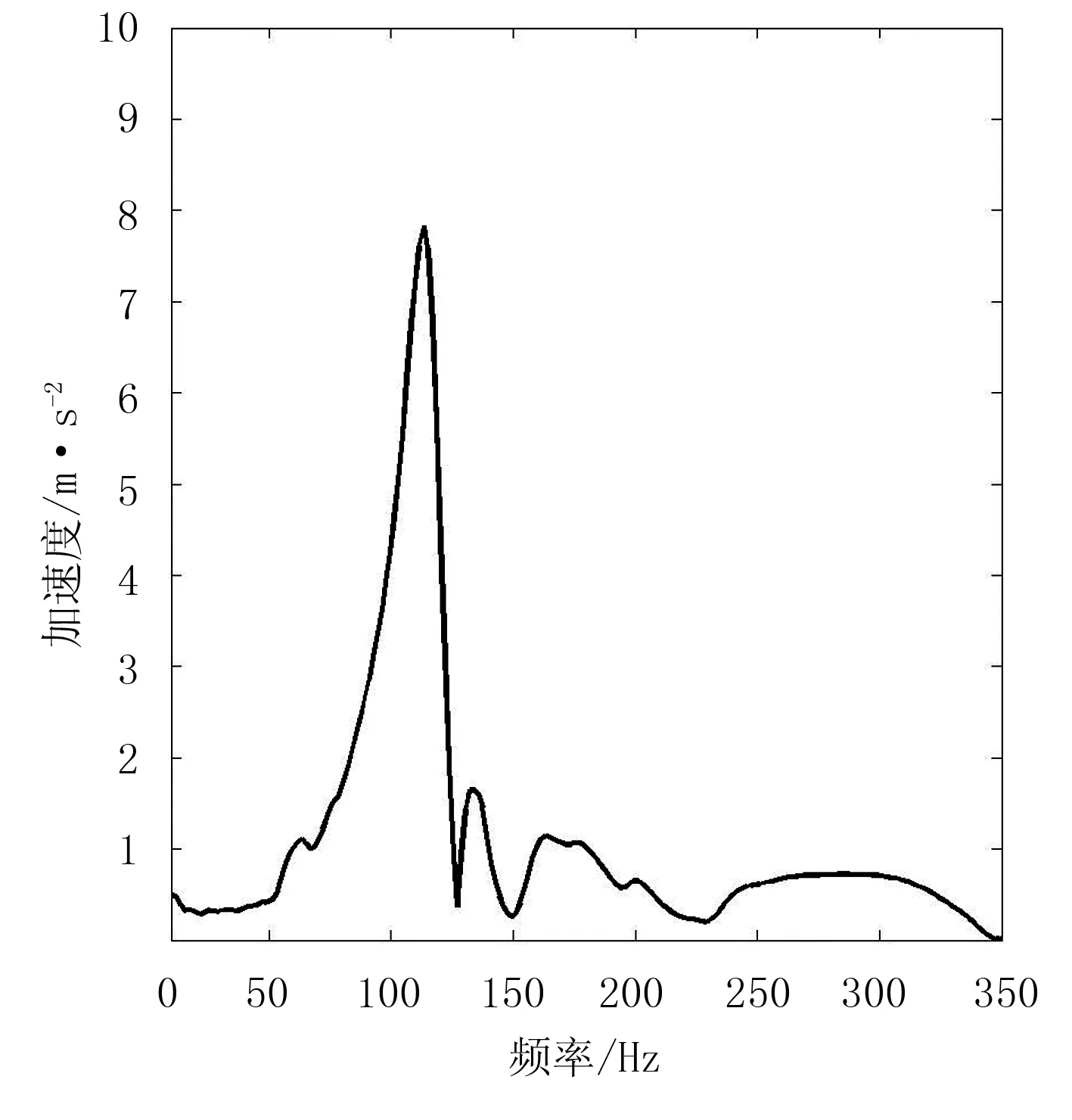
(b) 振動加速度頻域響應

密度/kg·m-3楊氏模量/MPa泊松比阻尼比果實10700．750．450-樹枝727．7113140．3480．04

2.2 果實幾何模型的建立

沙棘果實近似為橢圓形狀，為了建立精確的果實幾何模型，用貝塞爾曲線來模擬果實的輪廓。貝塞爾曲線法是建立曲線特征多邊形，只要移動多邊形頂點的位置，就能夠方便地改變曲線的形狀，使曲線很快收斂于要求的形狀[20]。它通過控制曲線上的4個點來編輯圖形，所以能較為精準地模擬果實輪廓。貝塞爾曲線方程為

B(t)=p0(1-t)3+3p1t(1-t)2+

3p2t2(1-t)+p3,t∈[0,1]

(12)

其中，p0、p1、p2、p3分別為4個控制點的坐標。為了得出果實輪廓的曲線方程，先將沙棘果實圖片導入軟件AutoCAD中，用樣條曲線控制點方式模擬外輪廓得出曲線的12個控制點坐標，然后把坐標代入方程(12)得到每段輪廓曲線的函數方程。運用三維建模軟件Pro/E的函數功能創建已知輪廓曲線的三維果實模型，沙棘果實樣本來自新疆青河縣林管站國家大果沙棘良種基地，品種為俄羅斯大果沙棘“楚依”。選取了20個果實樣本，其中3個樣本的三維模型圖如圖3(a)所示。

(a) (b)

2.3 果實果柄系統模態分析

模態分析是研究結構動力特性一種近代方法，每一個模態具有特定的固有頻率、阻尼比和模態振型。這些模態參數可以由計算或試驗分析取得，這樣一個計算或試驗分析過程稱為模態分析[21]。模態分析的目的是描述系統的動態特性，在時域里，系統的模態參數是獨立于外部條件的。

為了更加真實地模擬果實果柄系統，將果實和果柄分割為兩個實體，再用不同的材料劃分網格，第1個果實模型的網格劃分與約束如圖3(b)所示。模態分析采用Block Lanczos法，在樹枝下端施加了零位移約束。此有限元模型由23 453個單元和5 032個節點組成的多自由度結構，所以其有多個固有頻率和模態振型。而在振動采收時頻率太高會造成樹體的損傷，故提取了前6階低階固有頻率。

3 結果與分析

3.1 模態振型圖分析

振型是指體系的一種固有的特性，與固有頻率相對應。每一階固有頻率都對應一種振型。振型對應于頻率而言，一個固有頻率對應于一個振型，其中前6階模態振型圖如圖4所示。沙棘果實脫落一般是從果柄與樹枝的連接處脫落，所以振動能量主要集中在果柄區域或果實上部，才有可能使果實脫落。由以上模態振型圖可以看出：第3階模態的變形能量主要集中在果實中間的大部分區域，第4階和第5階模態振型圖的變形能量主要集中在果實的上部，而其余階模態都集中在離果柄比較遠的區域，故第3～5階頻率被作為振動收獲的可行性區域。

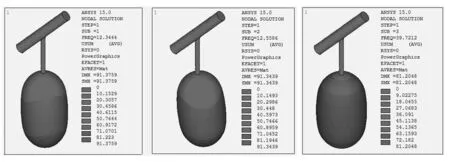
(a) 第1階 (12.34Hz) (b) 第2階 (12.56Hz) (e) 第3階 (39.72Hz)

(f) 第4階 (246.79Hz) (g) 第5階 (299.02Hz) (h) 第6階 (300.30Hz)

3.2 系統固有頻率回歸分析

20個樣本模型的固有頻率如表2所示。從表2可以看出：每個樣本的固有頻率都不一樣，因為每個果實幾何結構都不一樣。果實幾何參數主要有果柄長度、果柄直徑及果實體積。為了尋找果實頻率與果實體積、果柄長度、果柄直徑之間的關系，為以后進一步分析提供預測，建立回歸模型。

設系統固有頻率為y，果實長度為x1，果柄直徑為x2，果柄直體積x3，分別建立第3～5階頻率的三元回歸模型如下：

第3階y3=10.04+1.09x1+51.67x2-0.03x3

第4階y4=202.85+3.11x1+121.05x2-0.16x3

第5階y5=220.77-18.59x1+336.88x2-0.17x3

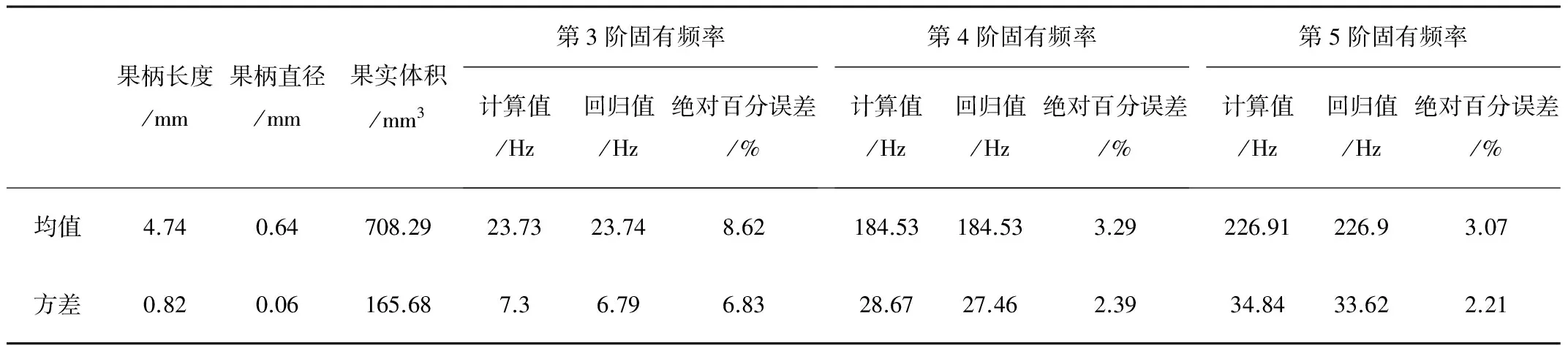
表2 果實樣本模型尺寸參數與固有頻率回歸模型誤差分析表

由表2可以得出：第3階、第4階、第5階固有頻率的計算值和回歸模型獲得的值都相差不大，相互之間沒有顯著性差異，且回歸模型獲得的值與計算值的平均絕對百分誤差也比較小；第3階回歸模型的百分誤差相對較大為8.62%，其他兩階模型的誤差都在3%左右。

4 結論

分析果實-果柄系統的受迫振動穩態解可知：果實的振動幅度隨著樹枝所受的采摘慣性力和采摘頻率的增大而增大，樹枝的振動幅度隨著果實質量的增加而減小。結合有限元模態分析得出的振型圖可知：在第3階共振頻率時，果實整體的振動幅度最大；在第4階和第5階共振頻率時，果實靠近果柄處的振動幅度比較大，但其對應的頻率比較高而不適合機械收獲。因此，在實際收獲中可選擇第3階頻率。

以果柄長度、果柄直徑及果實體積為變量的回歸模型的平均絕對百分誤差都在9%以內，因此對于不同幾何參數的果實均可通過此回歸模型初步預測果實果柄系統的固有頻率。

[1] 宋自娟，徐懷德，高錦明，等.加工過程中冷打漿沙棘濃縮濁汁理化特性的變化[J].農業工程學報，2014，30(3)：264-270.

[2] L M Bal, V Meda, S Naik, et al. Sea buckthorn berries:A potential source of valuable nutrients for nutraceuticals and cosmoceuticals[J].Food Research International, 2011, 44(7):1718-1727.

[3] 梁建平，慕后春，楊浩生.沙棘果實采收技術及裝備現狀分析[J].沙棘，2008，21(4)：17-20.

[4] H A Tinoco, D A Ocampo, F M Pea, et al.Finite element modal analysis of the fruit-peduncle of Coffea arabica L. var. Colombia estimating its geometrical and mechanical properties[J]. Computers and Electronics[J]. Agriculture, 2014，108: 17-27.

[5] S K J U Savary, R Ehsani, J K Schueller, et al. Simulation study of citrus tree canopy motion[J].Transac.ASABE, 2010, 53(5): 1373-1381.

[6] Z Láng.A one degree of freedom damped fruit tree model[J].Transactions of the ASABE, 2008, 51(3)：823-829.

[7] S K Upadhyaya, J R Cooke, R H Rand. Limb Impact Harvesting, Part I: Finite Element Analysis[J].Transactions of ASAE, 1981, 24(4): 856-863.

[8] R Fridley, C Yung. Computer analysis of fruit detachment during tree shaking[J].Transactions of the ASAE, 1975, 18(3):409-415.

[9] 李有堂.機械振動理論與應用[M].北京：科學出版社，2012.

[10] J Khazaei, D D Mann. Effects of Temperature and Loading Characteristics on Mechanical and Stress Relaxation Properties of Sea Buckthorn Berries. Part 2. Compression Tests[J].Agricultural Engineering International: CIGR Journal, 2004.

[11] 尚大軍，段新芳，楊中平，等.兩種無損檢測方法對CCA處理材的性能評價比較[J].木材工業，2008，22(2): 17-19.

[12] 張厚江，申世杰，崔英穎，等.振動方式測定木材彈性模量[J].北京林業大學學報，2005(6)：91-94.

[13] 劉鎮波，劉一星，于海鵬，等.實木板材的動態彈性模量檢測[J].林業科學，2005(6)：129-134.

[14] 賀磊盈.面向振動采收的果樹枝干三維重建方法及其動力學特性研究[J].杭州：浙江理工大學，2014.

[15] 清華大學固體力學教研組.機械振動[M].北京：機械工業出版社，1980.

[16] 阮錫根，余觀夏.木材物理學[M].北京：中國林業出版社，2005.

[17] 陳守謙.用衰減振動法測定木材的阻尼參數[J].林業科技，1990(4)：31-33.

[18] 陳守謙，張曉兵.受迫振動時木材阻尼參數的研究[J].林業科技，1992(2)：36-38.

[19] 張祖媛.貝塞爾曲線的幾何構型[J].四川工業學院學報，1998(4)：33-36，45.

[20] X Tang, J Ren，C Liu, et al, Simulation of Vibration Harvesting Mechanism for Wolfberry, ASABE Annual International Meeting[C]//2011 Louisville Kentucky USA，2011.

Mechanism Analysis and Simulation of Vibration Harvesting of the Sea Buckthorn Fruit-stalk System

Peng Jun, Sun Shipeng, Feng Yali, Yang Yougang, Fu Longsheng

(College of Mechanical and Electronic Engineering, Northwest A&F University, Yangling 712100 China)

Sea buckthorn is an ideal plant for ecological management and was thus planted widely in the western of China. Its fruit is rich in nutrition, and has high economic value, but sea buckthorn fruit is very difficult to be harvested. In order to change the situation mainly by manual picking, it is necessary to study the mechanized harvesting of sea buckthorn. In this paper, the mechanism of fruit-stalk detachment by vibration was studied, and a two degree of freedom forced vibration physical model is established and derive the kinetic equation. The steady forced vibration solution and the inertia detachment force of the fruit-stalk system were obtained by solving mathematical differential equations. Meanwhile, the geometric outline of fruit, of fruit is simulated by Bessel's function curve, and the geometric curve equation of the fruit were used to draw the 3D model of the fruit in Pro/E. Afterwards, the fruit model was introduced into the finite element analysis software ANSYS to carry out Modal analysis. The results show that the displacement, velocity and acceleration of the fruit-stalk system were in conformity with the results of finite element simulation analysis. When the frequency is in the range of 18～46Hz, the part of the fruit is resonant and the main mode is the largest. This will provide the theoretical basis for the development of the vibration picking equipment for sea buckthorn fruit.

fruit-stalk; vibration harvest; finite element; model analysis

2007-06-07

國家自然科學基金項目(31301242)；中國博士后科學基金項目(2015M572602)；陜西省自然科學基礎研究計劃-青年人才項目(2015JQ3065)；教育部留學歸國人員科研啟動基金項目(K308021401)

彭 俊(1991-)，男，陜西安康人，碩士研究生，(E-mail)jxpengjun@nwsuaf.edu.cn。

傅隆生(1984-)，男，江西吉安人，副教授，博士，碩士生導師，(E-mail)fulsh@nwsuaf.edu.cn。

S225.93

A

1003-188X(2017)07-0028-06