一道數(shù)列綜合題的解法及變式探究

■江西省豐城中學(xué) 吳愛龍 劉衛(wèi)琴

一道數(shù)列綜合題的解法及變式探究

■江西省豐城中學(xué) 吳愛龍 劉衛(wèi)琴

1.試題呈現(xiàn)

設(shè)數(shù)列{an}的前n項(xiàng)和為Sn,n∈N*,已知a1=1,a2=,且當(dāng)n≥2時(shí), 4Sn+2+5Sn=8Sn+1+Sn-1。

(1)求a4的值;

(3)求數(shù)列{an}的通項(xiàng)公式。

這是一道求數(shù)列相關(guān)問題的綜合試題,考查了轉(zhuǎn)化化歸思想與構(gòu)造新數(shù)列的能力,是不可多得的好題。

2.解法剖析

這里對第一問、第三問不詳解,主要談第二問的幾種解法。

數(shù)列{an·2n}是首項(xiàng)為2,公差為4的等差數(shù)列,即an·2n=4n-2,an=

這是處理在已知Sn條件下求an問題的一種常規(guī)解法。但由于遞推關(guān)系式中含有數(shù)列{an}中相鄰四項(xiàng),需兩次觀察、構(gòu)造才能做好,很多同學(xué)至此大都思路中斷。我們不妨換個(gè)角度去思考,或許會(huì)“柳暗花明”。

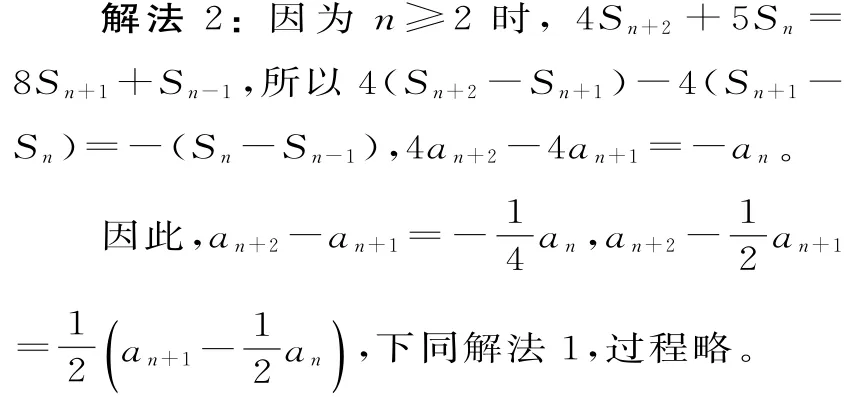
上述解法可謂一氣呵成,需要同學(xué)們通過認(rèn)真觀察、思考并根據(jù)系數(shù)特征才能想得出來。同學(xué)們平時(shí)學(xué)習(xí)中應(yīng)注重基礎(chǔ),不可過分追求一些技巧性太強(qiáng)的解法。

解法3：因?yàn)閚≥2時(shí),4Sn+2+5Sn=8Sn+1+Sn-1,所以4(Sn+2-Sn+1)-5(Sn+1-Sn)=-Sn+1+Sn-1,4an+2-5an+1=-(an+1+an)。

則4an+2-4an+1=-an,下同解法1,過程略。

這種解法從本題的實(shí)際出發(fā)“量身定做”,既不落俗套,又淡化了“湊項(xiàng)”的技巧。關(guān)鍵的一步變形4(Sn+2-Sn+1)-5(Sn+1-Sn)=-(Sn+1-Sn-1)在情理之中。

由此可得以下解法。

解法4：因?yàn)閚≥2時(shí),4Sn+2+5Sn=8Sn+1+Sn-1,所以4(an+2+an+1+an+Sn-1)+5(an+Sn-1)=8(an+1+an+Sn-1)+Sn-1。

整理得4an+2-4an+1=-an。

下同,過程略。

上述解法簡單至極,其之所以“簡”,是因?yàn)槟芊佃睔w真,回歸到最基本的關(guān)系式an=

3.變式拓廣

下面將題目作些變式探究。

變式1：設(shè)數(shù)列{an}的前n項(xiàng)和為Sn,n∈N*。已知a1=1,a2=且當(dāng)n≥2時(shí),4Sn+3-12Sn+2+13Sn+1-6Sn+Sn-1=0,求數(shù)列{an}的通項(xiàng)公式。

解：當(dāng)n≥2時(shí),4Sn+3-12Sn+2+13Sn+1-6Sn+Sn-1=0,故:

4(an+3+an+2+an+1+an+Sn-1)-12(an+2+an+1+an+Sn-1)+13(an+1+an+Sn-1)-6(an+Sn-1)+Sn-1=0。

整理得:

4an+3-8an+2+5an+1-an=0。

變形得:

4an+3-4an+2+an+1=4an+2-4an+1+an。

4a4-4a3+a2=4a3-4a2+a1=0。

故4an+2-4an+1+an=0,n∈N*。

(責(zé)任編輯 徐利杰)