基于Spark框架的電力大數(shù)據(jù)清洗模型*
王沖,鄒瀟
(1.國(guó)網(wǎng)內(nèi)蒙古東部電力有限公司信息通信分公司,呼和浩特010020;2.蘭州大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,蘭州730000)
0 引 言
電力大數(shù)據(jù)具有數(shù)量大、維度高,數(shù)據(jù)模式繁多等特征,在電力大數(shù)據(jù)的采集過(guò)程中,其不可避免的存在異常數(shù)據(jù),對(duì)電力大數(shù)據(jù)清洗有很強(qiáng)的必要性[1]。國(guó)內(nèi)外對(duì)電力大數(shù)據(jù)清洗研究主要有聚類和關(guān)聯(lián)分析[2]、條件函數(shù)依賴[3]、馬爾科夫模型[4]、DS證據(jù)理論[5]。大部分?jǐn)?shù)據(jù)清洗技術(shù)都需要依賴數(shù)據(jù)模型本身構(gòu)建異常數(shù)據(jù)識(shí)別規(guī)則,對(duì)檢測(cè)到的異常數(shù)據(jù)做刪除或均值填充處理,其缺點(diǎn)就是:破壞了數(shù)據(jù)的連續(xù)性、完整性、準(zhǔn)確性。
針對(duì)以上電力大數(shù)據(jù)清洗難點(diǎn),本文提出一種基于Spark框架的電力大數(shù)據(jù)清洗模型。相比一些電力大數(shù)據(jù)清洗模型,本文數(shù)據(jù)清洗模型減少人為干預(yù),不需要根據(jù)數(shù)據(jù)關(guān)系模式設(shè)定識(shí)別規(guī)則,異常識(shí)別算法依賴于歷史數(shù)據(jù)中的正常樣本數(shù)據(jù),且對(duì)異常數(shù)據(jù)修正是建立在其同一時(shí)間序列數(shù)據(jù)分析的基礎(chǔ)上,最終能夠?qū)崿F(xiàn)對(duì)歷史或?qū)崟r(shí)數(shù)據(jù)中的異常數(shù)據(jù)清洗。
1 基于Spark框架的電力大數(shù)據(jù)清洗模型
電力大數(shù)據(jù)清洗是對(duì)檢測(cè)到的電力大數(shù)據(jù)中異常數(shù)據(jù)進(jìn)行修正的過(guò)程,利用Spark框架構(gòu)建電力大數(shù)據(jù)清洗模型時(shí)分為以下幾個(gè)階段:數(shù)據(jù)準(zhǔn)備、正常簇樣本獲取、異常數(shù)據(jù)識(shí)別、異常數(shù)據(jù)修正、修正數(shù)據(jù)存儲(chǔ)。數(shù)據(jù)準(zhǔn)備即將存儲(chǔ)在傳統(tǒng)關(guān)系型數(shù)據(jù)庫(kù)中的數(shù)據(jù)轉(zhuǎn)存在適合于大數(shù)據(jù)處理的非關(guān)系型數(shù)據(jù)庫(kù)中,然后加載到Spark的彈性分布式數(shù)據(jù)集(RDD)中;通過(guò)抽取一定數(shù)量的電力大數(shù)據(jù)樣本,應(yīng)用層次聚類算法將其中的異常點(diǎn)抽取,獲取可用于實(shí)現(xiàn)邊界樣本異常識(shí)別算法的正常樣本簇;異常數(shù)據(jù)識(shí)別是建立在邊界樣本的基礎(chǔ)上,通過(guò)邊界樣本異常識(shí)別算法完成對(duì)電力大數(shù)據(jù)中的異常數(shù)據(jù)檢測(cè);異常數(shù)據(jù)修正完成對(duì)檢測(cè)到的電力大數(shù)據(jù)中的異常數(shù)據(jù)的修復(fù)。清洗步驟如下:
(1)數(shù)據(jù)準(zhǔn)備:將數(shù)據(jù)存儲(chǔ)在分布式文件系統(tǒng)HDFS中;
(2)從分布式文件系統(tǒng)上讀取數(shù)據(jù)并執(zhí)行cache操作生成RDDs,將數(shù)據(jù)讀入到內(nèi)存;
(3)利用改進(jìn)的并行 CURE聚類算法獲取正常簇;
(4)從正常簇中選取邊界樣本數(shù)據(jù);
(5)設(shè)計(jì)基于邊界樣本的異常數(shù)據(jù)識(shí)別算法,并對(duì)測(cè)試樣本識(shí)別異常數(shù)據(jù);
(6)標(biāo)記異常數(shù)據(jù)所在檢測(cè)樣本中的位置;
(7)對(duì)異常數(shù)據(jù)應(yīng)用指數(shù)加權(quán)移動(dòng)平均數(shù)進(jìn)行修正;
(8)形成修正數(shù)據(jù)集并保存。
基于spark框架的電力大數(shù)據(jù)清洗模型框架如圖1所示。
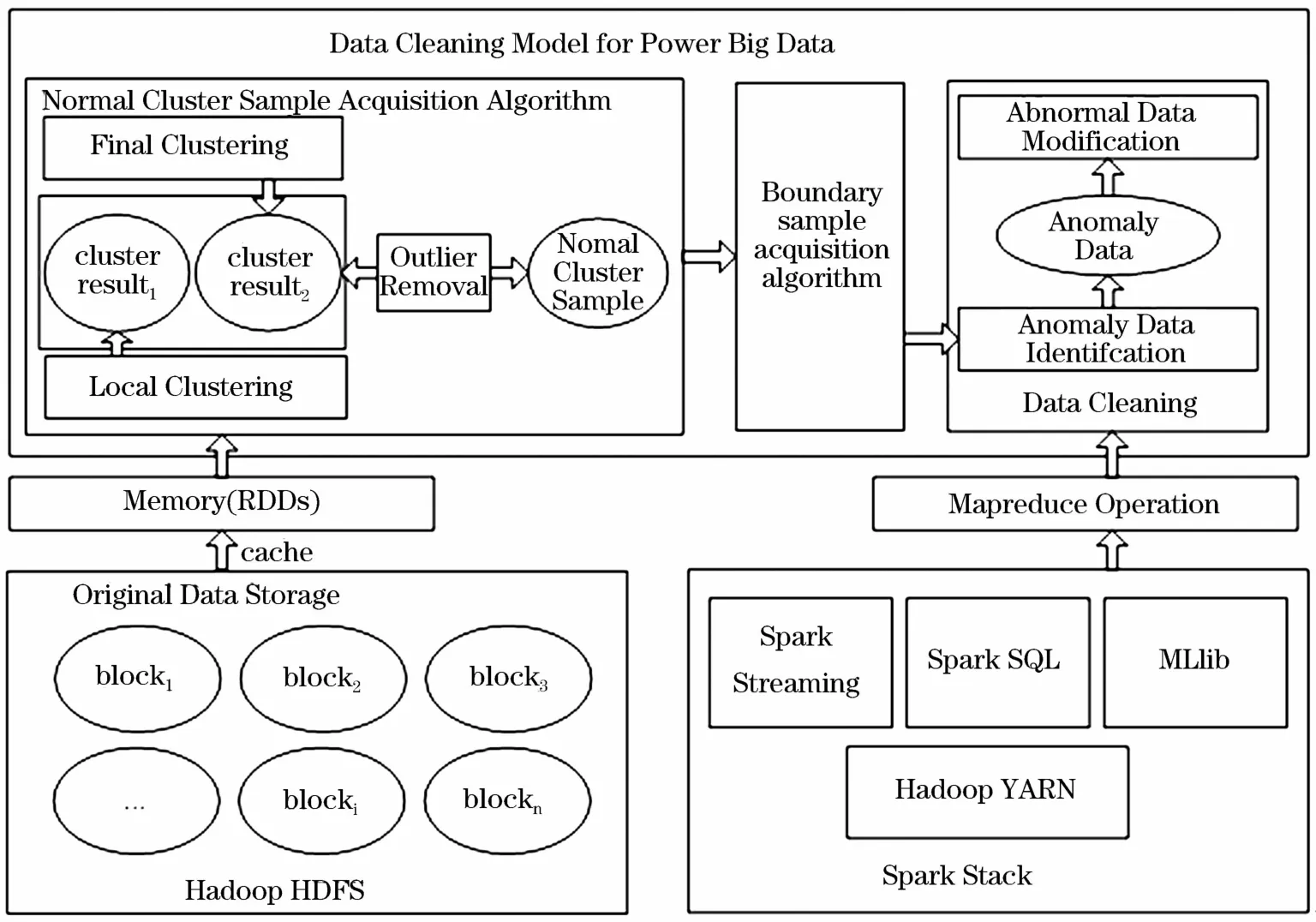
圖1 基于spark框架的電力大數(shù)據(jù)清洗模型Fig.1 Data cleaning model for power big data based on Spark framework
本文接下來(lái)針對(duì)電力大數(shù)據(jù)清洗模型中的幾個(gè)核心步驟進(jìn)行分析。首先詳細(xì)描述了改進(jìn)CURE聚類算法獲取正常簇;其次介紹了邊界樣本的選擇過(guò)程,并對(duì)邊界樣本的異常數(shù)據(jù)識(shí)別算法進(jìn)行了詳細(xì)分析;最后闡述了指數(shù)加權(quán)移動(dòng)平均數(shù)對(duì)異常數(shù)據(jù)進(jìn)行修正。本文在最后給出了實(shí)驗(yàn)驗(yàn)證及分析,并對(duì)本文工作進(jìn)行總結(jié)并指出進(jìn)一步的研究方向。
2 正常簇樣本獲取算法
在對(duì)電力大數(shù)據(jù)進(jìn)行異常識(shí)別時(shí),由于電力大數(shù)據(jù)在采集過(guò)程中采集設(shè)備具有數(shù)據(jù)校驗(yàn)功能,因此采集的數(shù)據(jù)大多為正常數(shù)據(jù),異常數(shù)據(jù)較少,同時(shí)電力大數(shù)據(jù)的種類繁多導(dǎo)致不能直接構(gòu)建單一規(guī)則或設(shè)定閾值進(jìn)行異常識(shí)別[9]。直接對(duì)采集上來(lái)的電力大數(shù)據(jù)進(jìn)行異常識(shí)別計(jì)算量大且識(shí)別效率低。因此可以從電力大數(shù)據(jù)歷史數(shù)據(jù)樣本中獲取正常樣本簇,在正常簇的邊界樣本集的基礎(chǔ)上對(duì)歷史或?qū)崟r(shí)電力大數(shù)據(jù)進(jìn)行異常識(shí)別,這種異常識(shí)別不依賴數(shù)據(jù)屬性閾值及屬性數(shù)學(xué)模式規(guī)則,同時(shí)可提高檢測(cè)的效率。
CURE聚類算法在對(duì)測(cè)試樣本進(jìn)行聚類時(shí)通過(guò)消除離群點(diǎn)降低對(duì)聚類結(jié)果的影響,可通過(guò)CURE聚類算法對(duì)測(cè)試樣本進(jìn)行聚類獲取正常樣本的聚類簇。CURE聚類算法分別在兩個(gè)階段對(duì)離群點(diǎn)進(jìn)行刪除:第一階段是在聚類增長(zhǎng)非常緩慢的類作為離群點(diǎn)刪除;第二階段是在聚類結(jié)束時(shí)將對(duì)象數(shù)據(jù)明顯少的類作為離群點(diǎn)刪除。但是通過(guò)CURE聚類算法對(duì)離群點(diǎn)進(jìn)行刪除時(shí)存在以下兩個(gè)問(wèn)題:
(1)很難對(duì)聚類過(guò)程中增長(zhǎng)緩慢的類做界定,對(duì)這里離群點(diǎn)何時(shí)刪除,如何界定增長(zhǎng)緩慢[7];
(2)對(duì)離群點(diǎn)刪除后因局部數(shù)據(jù)的分布特征存在掩蓋現(xiàn)象[8]。
針對(duì)CURE聚類算法剔除異常點(diǎn)時(shí)存在的問(wèn)題,本文使用離群程度用于判定離群點(diǎn),可有效解決增長(zhǎng)緩慢的離群類難界定及局部離群點(diǎn)被淹沒(méi)的現(xiàn)象。相關(guān)定義如下:
定義1:對(duì)每個(gè)劃分的數(shù)據(jù)塊進(jìn)行聚類,得到的數(shù)據(jù)簇表示為pi(mpi,wi),其中pi表示塊中第i個(gè)簇,表示為第i個(gè)簇的中心點(diǎn),mpi表示每個(gè)中心點(diǎn)的權(quán)重值,wi是每個(gè)簇中數(shù)據(jù)的個(gè)數(shù)。因此每個(gè)劃分的數(shù)據(jù)塊可以使用若干個(gè)代表,pi稱為代表點(diǎn)。
定義2:設(shè)代表點(diǎn)的集合為P,每個(gè)代表點(diǎn)pi的中心點(diǎn)到簇外任意一點(diǎn)的偏差距離表示為離群程:
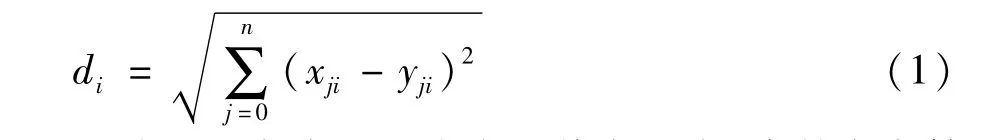
用歐氏距離表示一個(gè)點(diǎn)的偏離程度,當(dāng)某點(diǎn)離簇中心點(diǎn)越遠(yuǎn),則離群程度值越大。
定義3:設(shè)離群程度集為D,定義離群程度判定值為:

定義4:設(shè)離群參數(shù)為,離群程度最小值為:

定義5:對(duì)于離群程度集D中任意,若,則所對(duì)應(yīng)的代表點(diǎn)為離群點(diǎn),其所在的簇中的數(shù)據(jù)即為離群數(shù)據(jù)。
算法基本思想是:首先從數(shù)據(jù)集中抽取一個(gè)隨機(jī)樣本,且樣本的選擇應(yīng)該具有代表性;其次,將樣本劃分為若干個(gè)相同大小的數(shù)據(jù)集;對(duì)劃分完成首次聚類,得到m/q各簇,然后計(jì)算簇中每個(gè)點(diǎn)的離群程度判定值(AD)及離群參數(shù)(δ);刪除不滿足的離群點(diǎn);然后對(duì)m/q個(gè)簇進(jìn)行第二次聚類,同時(shí)刪除簇中樣本點(diǎn)明顯少的類,最后將所有剩余的數(shù)據(jù)點(diǎn)指定到最近的簇,完成聚類,得到正常簇樣本。
3 基于邊界樣本的異常數(shù)據(jù)識(shí)別算法
本文提出了基于邊界樣本的異常數(shù)據(jù)識(shí)別算法,首先通過(guò)獲取正常簇的邊界樣本集;然后根據(jù)異常數(shù)據(jù)識(shí)別算法檢測(cè)異常數(shù)據(jù);最后標(biāo)記異常數(shù)據(jù)并記錄所在位置。異常數(shù)據(jù)識(shí)別是對(duì)電力大數(shù)據(jù)中歷史或?qū)崟r(shí)流數(shù)據(jù)中的異常數(shù)據(jù)檢測(cè)的過(guò)程,是建立在正常簇的邊界樣本的基礎(chǔ)上。每個(gè)正常簇的邊界樣本必須具有以下特點(diǎn):(1)距離質(zhì)心最遠(yuǎn);(2)分散在正常樣本的四周;(3)能夠代表正常樣本的形狀。
對(duì)于正常簇樣本如何保證其選擇的邊界樣本點(diǎn)能夠分散在正常簇樣本的四周,符合邊界樣本分布特點(diǎn),下面給出其相關(guān)數(shù)學(xué)證明。
證明1:在一個(gè)三角形中,位于底邊中垂線上的頂點(diǎn)使得到其底邊兩點(diǎn)距離之和最短,且周長(zhǎng)最短。圖2給出了三角形頂點(diǎn)在中垂線上和不在中垂線上的情況。
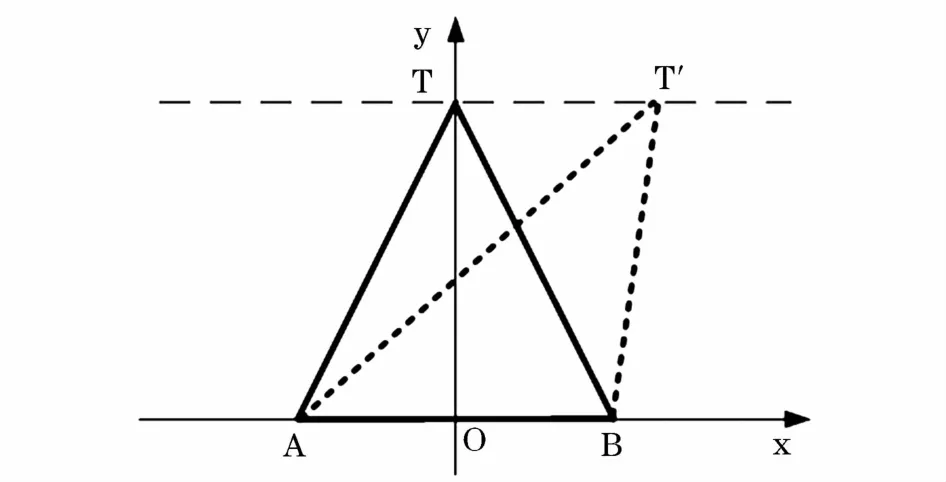
圖2 三角形頂點(diǎn)分布Fig.2 Triangle vertex distribution
在三角形TAB中,高為b,底邊|AB|=2a,頂點(diǎn)坐標(biāo)為T(x,b),現(xiàn)在需要證明位于中垂線上的頂點(diǎn)T使得|TA|+|TB|值最小。根據(jù)公式可得:
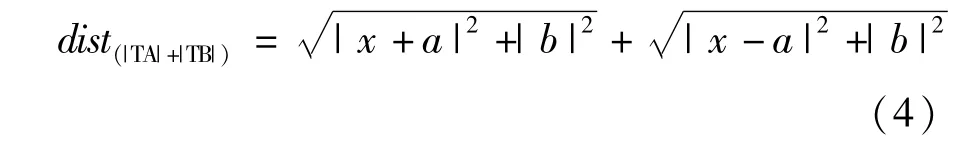
公式兩邊求導(dǎo)數(shù)可得:

通過(guò)對(duì)公式求極值,當(dāng)x=0時(shí),可以得到distance(|TA|+|TB|)取得極小值,。
證明2:橢圓上一點(diǎn)M使得到橢圓上其他兩點(diǎn)C和B距離之和最大。
圖3給出了橢圓形數(shù)據(jù)節(jié)點(diǎn)的分布示意。
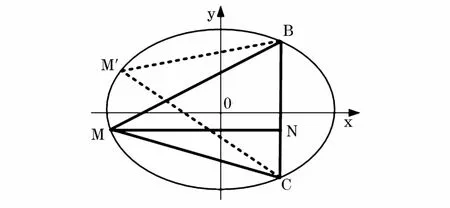
圖3 橢圓型數(shù)據(jù)點(diǎn)分布Fig.3 Elliptic data point distribution
長(zhǎng)軸長(zhǎng)為2m,短軸長(zhǎng)為2n,|BC|=2a,設(shè)MN為距離BC最遠(yuǎn)點(diǎn)所在的直線,|MN|=b,假設(shè)M`為距離邊BC兩個(gè)短點(diǎn)距離之和最大的點(diǎn),根據(jù)證明可以得出。

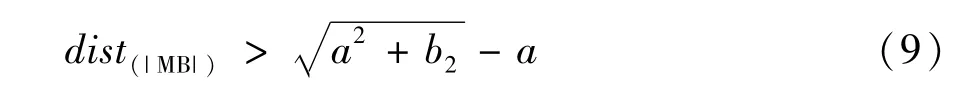
通過(guò)式(7)可以看出M`不會(huì)出現(xiàn)在B、C半徑為周圍。因此如果選擇B、C作為代表點(diǎn),M`也可以作為代表點(diǎn),使得M`、B、C作為代表點(diǎn)足夠分散。
在對(duì)邊界樣本點(diǎn)進(jìn)行選擇時(shí),應(yīng)保持邊界樣本點(diǎn)的特點(diǎn),下面給出邊界樣本的選擇過(guò)程:
步驟1:計(jì)算簇的中心點(diǎn),m為簇的點(diǎn)個(gè)數(shù);
步驟2:第一個(gè)邊界樣本點(diǎn)為離中心點(diǎn)最遠(yuǎn)的點(diǎn),第二個(gè)邊界樣本點(diǎn)為離第一樣本點(diǎn)最遠(yuǎn)的點(diǎn),i為最大點(diǎn)距離下標(biāo),j第二個(gè)樣本點(diǎn)下標(biāo);
步驟3:接下來(lái)選擇的邊界樣本為離前兩個(gè)樣本點(diǎn)距離之和最大的點(diǎn),直到選取的樣本點(diǎn)能夠代表聚類簇,則選擇停止。
正常簇的邊界樣本選擇過(guò)程如圖4所示。
式(4)~式(6)經(jīng)過(guò)加減處理后可得:
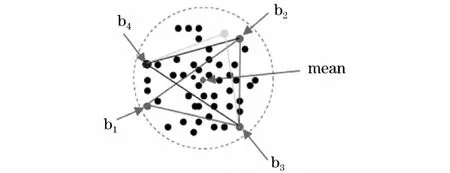
圖4 正常樣本簇的邊界樣本選擇過(guò)程Fig.4 Selection process of border cluster sample of normal sample
設(shè)正常簇樣本的邊界樣本集為B={b1,b2,…,bn},正常簇樣本的邊界樣本集的獲取已在上文提及,正常簇樣本的識(shí)別半徑為rs。待測(cè)試樣本為T={t1,t2,…,tm},該測(cè)試樣本可為信息機(jī)房監(jiān)測(cè)數(shù)據(jù)歷史樣本或信息機(jī)房實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)。S為識(shí)別出的非異常監(jiān)測(cè)信息,N為識(shí)別出的異常監(jiān)測(cè)信息。
以邊界樣本集作為平面檢測(cè)器,異常信息識(shí)別規(guī)則表示為:

式中l(wèi)1為待識(shí)別樣本點(diǎn)到邊界樣本的距離序列最小值;l2為待識(shí)別樣本到邊界樣本距離最遠(yuǎn)點(diǎn)距離值;dm為待識(shí)別樣本到質(zhì)心距離;r為正常簇樣本的識(shí)別半徑。
邊界樣本點(diǎn)分散在聚類簇的四周,能夠表示聚類簇的形狀。利用正常簇的邊界樣本來(lái)識(shí)別待檢測(cè)樣本,可以減少異常識(shí)別算法的計(jì)算量。針對(duì)異常信息識(shí)別規(guī)則,基于邊界樣本的異常識(shí)別算法的具體實(shí)現(xiàn)步驟如下:
算法輸入:待識(shí)別樣本T={ti,i∈[1,m],m為待識(shí)別樣本總數(shù)},邊界樣本集B={bj,j∈[1,n],n為邊界樣本總數(shù)},正常簇樣本ki的質(zhì)心m;
算法輸出:異常數(shù)據(jù)信息Q;
步驟1:計(jì)算待識(shí)別樣本點(diǎn)ti到邊界樣本點(diǎn)bj的距離,構(gòu)成距離序列dist,dist={d1,d2,…,dn};
步驟2:計(jì)算正常簇樣本的識(shí)別半徑rs;
步驟3:查找距離序列dist中最小值l1=min(di);
步驟4:在邊界樣本里查找與待識(shí)別樣本點(diǎn)ti距離最遠(yuǎn)點(diǎn)bk,計(jì)算ti到bk距離l2=distance(ti,bk);
步驟5:如果l1>=l2,則待識(shí)別樣本點(diǎn)ti為異常數(shù)據(jù);若l1<l2,則執(zhí)行步驟6;
步驟6:計(jì)算ti到正常簇樣本ki的質(zhì)心m的距離,dim=distance(ti,m);
步驟7:如果dim>rs,則待識(shí)別樣本點(diǎn)ti為異常數(shù)據(jù);若dim<=rs,則待識(shí)別樣本點(diǎn)ti為正常數(shù)據(jù);
步驟8:標(biāo)記異常數(shù)據(jù)所在樣本中的位置,并將信息進(jìn)行反饋;
步驟9:重復(fù)執(zhí)行步驟1~步驟8,直到所有待識(shí)別樣本都識(shí)別完畢;
步驟10:輸出所有異常信息,并做下一步處理。
通過(guò)邊界樣本異常識(shí)別算法,在進(jìn)行異常識(shí)別時(shí),不必設(shè)置異常識(shí)別的閾值,同時(shí)可以避免因使用數(shù)據(jù)模式帶來(lái)的復(fù)雜性,可以提高異常識(shí)別的效率。
4 基于時(shí)間序列分析異常數(shù)據(jù)修正
電力大數(shù)據(jù)是在一定時(shí)間周期內(nèi)采集的數(shù)據(jù)的積累,電力大數(shù)據(jù)因其種類多,隨時(shí)間變化一般呈現(xiàn)三種規(guī)律:周期變化型數(shù)據(jù)、幅值變化較小型數(shù)據(jù)、緩慢增加型數(shù)據(jù)[10]。
對(duì)異常數(shù)據(jù)進(jìn)行修正時(shí)要根據(jù)異常數(shù)據(jù)所在數(shù)據(jù)區(qū)間數(shù)據(jù)特點(diǎn)及異常數(shù)據(jù)表現(xiàn)形式,對(duì)不同類型的異常數(shù)據(jù)進(jìn)行分析修正。對(duì)緩慢增加或衰減型電力大數(shù)據(jù)中的異常數(shù)據(jù)進(jìn)行修正時(shí),選取的參考數(shù)據(jù)序列為異常數(shù)據(jù)所在序列的[n,m]區(qū)間;對(duì)周期性變化型電力大數(shù)據(jù)中的異常數(shù)據(jù)進(jìn)行修正時(shí),選取的數(shù)據(jù)序列為包含異常數(shù)據(jù)在內(nèi)的n個(gè)周期內(nèi)的異常數(shù)據(jù)所在的時(shí)刻t的數(shù)據(jù)序列。
在對(duì)異常數(shù)據(jù)進(jìn)行修正時(shí),一般采用的方法是使用該異常數(shù)據(jù)所在序列的平均數(shù)進(jìn)行代替。這時(shí)修正的值為,式中xi是對(duì)給定的一個(gè)權(quán)值。但是,某一序列值對(duì)后面序列值的影響作用是衰減的,而不是一直是。因此對(duì)異常數(shù)據(jù)進(jìn)行修正采用指數(shù)加權(quán)移動(dòng)平均數(shù):

5 實(shí)驗(yàn)及結(jié)果分析
本文采用“Spark On Yarn”集群模式構(gòu)建電力大數(shù)據(jù)清洗模型實(shí)驗(yàn)環(huán)境,實(shí)驗(yàn)采用6臺(tái)服務(wù)器組成數(shù)據(jù)清洗集群節(jié)點(diǎn),其中一個(gè)節(jié)點(diǎn)為Master,其余五個(gè)節(jié)點(diǎn)分別為 Slave1-Slave5,每個(gè)節(jié)點(diǎn)的配置見表2。每個(gè)服務(wù)器節(jié)點(diǎn)采用Ubuntu-12.04.1操作系統(tǒng),使用 Hadoop-2.6.0,Spark-1.3.1,Scala-2.10.5,JDK-1.7.0_79搭建節(jié)點(diǎn)的軟件環(huán)境。實(shí)驗(yàn)平臺(tái)在Scala的Intellij Idea開發(fā)環(huán)境上進(jìn)行開發(fā)實(shí)現(xiàn),以hadoop的hdfs實(shí)現(xiàn)數(shù)據(jù)結(jié)果的存儲(chǔ)。
以某風(fēng)電場(chǎng)風(fēng)力發(fā)電監(jiān)測(cè)數(shù)據(jù)作為數(shù)據(jù)清洗研究對(duì)象。該風(fēng)力發(fā)電監(jiān)測(cè)數(shù)據(jù)大小為5 GB,分別從5臺(tái)風(fēng)力發(fā)電機(jī)采集,采集間隔為1 s,記錄了從2012年2月1日到2012年2月29日風(fēng)力發(fā)電監(jiān)測(cè)數(shù)據(jù)。
集群配置具體如下:
服務(wù)器類型:刀片型。服務(wù)器數(shù)量:6。
內(nèi)存:6×128 GB。CPU核數(shù):6×16。
網(wǎng)卡速率:1 Gbit/s。硬盤容量:6×1 T。
處理器類型:Intel Xeon 2.00 GHz。
本文將從異常識(shí)別的準(zhǔn)確性、異常修正的效率對(duì)電力大數(shù)據(jù)清洗模型進(jìn)行驗(yàn)證分析。
實(shí)驗(yàn)1:針對(duì)正常樣本獲取過(guò)程中離群點(diǎn)刪除算法,本文測(cè)試了幾種離群點(diǎn)檢測(cè)算法的檢測(cè)率和誤檢率,測(cè)試結(jié)果見表1。與Apriori算法相比,本文算法在檢測(cè)率相似的情況下,誤檢率較低。
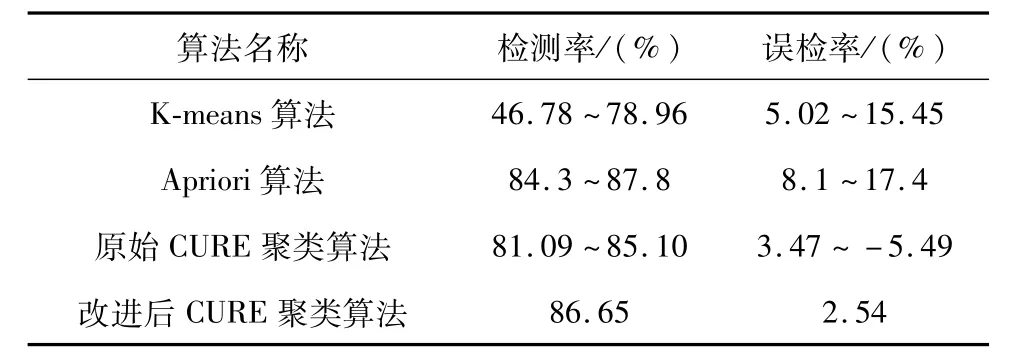
表1 離群點(diǎn)檢測(cè)算法比較Tab.1 Comparison of outlier detection algorithms
實(shí)驗(yàn)2:為了驗(yàn)證電力大數(shù)據(jù)異常識(shí)別算法的檢測(cè)異常數(shù)據(jù)正確性,實(shí)驗(yàn)保持集群節(jié)點(diǎn)數(shù)固定,不斷調(diào)整測(cè)試數(shù)據(jù)樣本大小,檢測(cè)算法的準(zhǔn)確率,結(jié)果如表2所示。模型檢測(cè)到了大部分的異常數(shù)據(jù)。
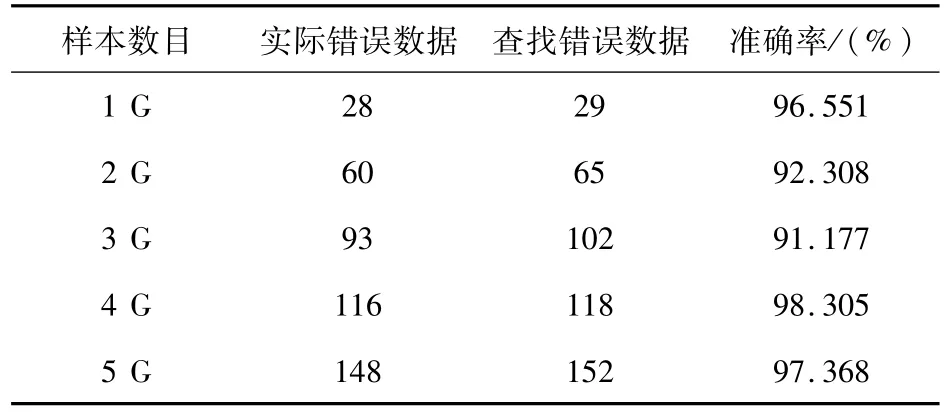
表2 電力大數(shù)據(jù)異常識(shí)別算法的準(zhǔn)確率測(cè)試Tab.2 Accuracy test of power big data anomaly identification algorithm
實(shí)驗(yàn)3:為了驗(yàn)證電力大數(shù)據(jù)清洗模型的高效性,測(cè)試了傳統(tǒng)單機(jī)數(shù)據(jù)清洗與基于Spark框架的電力大數(shù)據(jù)清洗模型不同數(shù)量的清洗所需要的時(shí)間。集群節(jié)點(diǎn)數(shù)固定,不斷調(diào)整待清洗數(shù)據(jù)樣本大小,測(cè)試數(shù)據(jù)清洗時(shí)間,測(cè)試結(jié)果見表3。

表3 單機(jī)及并行數(shù)據(jù)清洗清洗時(shí)間比較Tab.3 Cleaning time comparison of single with parallel data cleaning
實(shí)驗(yàn)4:固定測(cè)試數(shù)據(jù)樣本大小,從中隨機(jī)抽取15 000條數(shù)據(jù)作為實(shí)驗(yàn)測(cè)試樣本,正常簇樣本個(gè)數(shù)為5,每個(gè)正常樣本簇的邊界樣本個(gè)數(shù)分別為25,35,45,55,65,在待識(shí)別樣本數(shù)目固定的情況下,對(duì)上述測(cè)試樣本采用基于邊界樣本的異常信息識(shí)別方法進(jìn)行異常信息識(shí)別,檢測(cè)正常樣本簇的邊界樣本個(gè)數(shù)對(duì)檢測(cè)結(jié)果的影響,結(jié)果如表4所示。
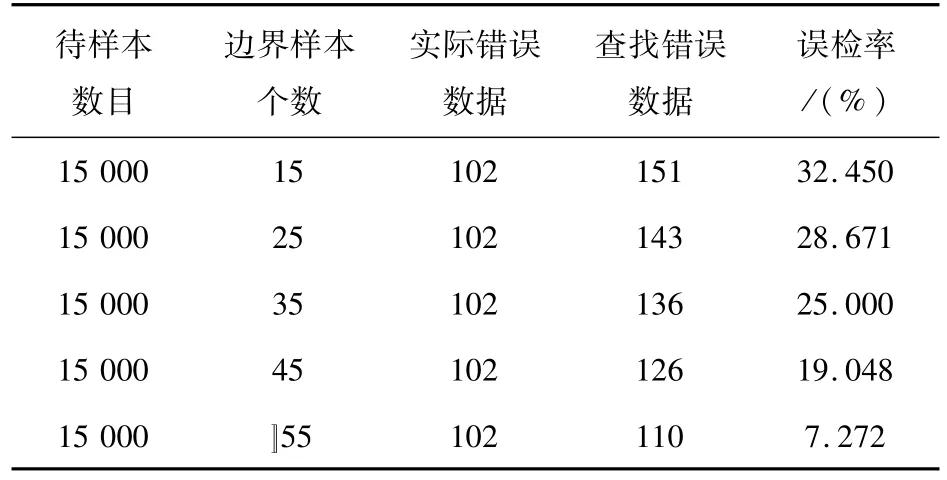
表4 基于邊界樣本的異常信息識(shí)別方法實(shí)驗(yàn)結(jié)果Tab.4 Experimental results of information identifying based on abnormal samples boundaries
6 結(jié)束語(yǔ)
本文分析了電力大數(shù)據(jù)清洗過(guò)程中的若干難點(diǎn),并針對(duì)電力大數(shù)據(jù)的特點(diǎn)及清洗難點(diǎn)提出了基于Spark框架的電力大數(shù)據(jù)清洗模型。該清洗模型具有以下特點(diǎn):
(1)異常數(shù)據(jù)識(shí)別無(wú)須外源數(shù)據(jù);
(2)異常數(shù)據(jù)識(shí)別及修正準(zhǔn)確性高;
(3)利用并行Spark大數(shù)據(jù)處理框架,具有高效性。但是,本文在選取正常簇的邊界樣本時(shí)仍然存在問(wèn)題,即何時(shí)達(dá)到最優(yōu)邊界樣本數(shù);其次,對(duì)異常數(shù)據(jù)的修正是建立在同一時(shí)間序列的樣本上,若該時(shí)間序列出現(xiàn)異常對(duì)異常數(shù)據(jù)修正的準(zhǔn)確性仍會(huì)有影響。針對(duì)以上解決問(wèn)題需要在以后的工作中進(jìn)一步探討優(yōu)化并完善電力大數(shù)據(jù)清洗模型。

