復合材料單面加固修補鋼板的界面應力分析

黃凌凱，章向明，王安穩

(海軍工程大學 理學院，湖北 武漢 430033)

復合材料單面加固修補鋼板的界面應力分析

黃凌凱，章向明，王安穩

(海軍工程大學 理學院，湖北 武漢 430033)

復合材料加固修復鋼結構技術有許多優點和廣闊的應用前景，該方法的關鍵在于保證復合材料補片和鋼板的連接界面具有良好的粘接性能。文章為探究粘接界面的力學性能，利用ANSYS軟件建立二維線彈性有限元模型，模擬碳纖維增強復合材料(CFRP)單面加固鋼板的拉伸試驗過程，分析粘接界面的應力分布情況及其變化規律，研究膠層彈性模量，膠層厚度以及CFRP補片厚度對膠層界面應力的影響，為確定最優的加固方案提供理論依據。分析結果表明：膠層端部區域的剪應力和剝離應力隨著膠層彈性模量和CFRP補片厚度的增加而增大，適當地增加膠層厚度有利于提高加固效果。

復合材料；單面加固；膠層應力；膠層彈性模量；CFRP補片厚度；膠層厚度

碳纖維增強復合材料(CFRP)具有比強度和比剛度高，耐腐蝕、抗疲勞性能好等優異的力學性能，已被廣泛應用于橋梁、管道、船舶等鋼結構的加固和修復工程中。CFRP加固法即為用粘接劑將CFRP補片粘貼于鋼結構表面，通過膠層傳遞載荷使CFRP和鋼結構共同受力，從而改善原結構受損部位的應力狀態，增強原結構的極限強度和承載能力。相較于傳統的鋼結構加固修復技術，CFRP加固法施工便捷，能保持原結構的整體性，且加固后結構不會產生嚴重的應力集中現象。

國內外學者對CFRP加固鋼結構進行了大量的研究，馬建勛等人[1]進行了CFRP布加固鋼板的單軸拉伸試驗，結果表明加固后鋼板的屈服載荷和極限承載能力均有大幅度提高。李耘宇等人[2]通過試驗發現隨著碳纖維布層數的增加，鋼試件的屈服載荷逐漸增大。Colombi等人[3]的試驗表明鋼板和CFRP的脫膠分離是加固結構的主要破壞模式。Bocciarelli等人[4]的研究表明CFRP和鋼板的脫膠破壞從端部開始并向中間擴展直至完全脫粘。吳剛等人[5]的試驗發現使用CFRP加固鋼梁能夠大幅度提高其疲勞壽命，且CFRP板彈性模量越高加固效果越好。Jones等人[6]研究發現使用CFRP雙面加固后含裂紋鋼板的疲勞壽命有了極大的提高，且單面加固的效果不如雙面加固。鄭云等人[7]建立了CFRP板單面加固含中央裂紋鋼板的有限元模型，研究了補片和膠層參數對加固效果的影響，結果表明CFRP板的寬度、厚度和彈性模量越大，膠層的剪切模量越大、厚度越小，加固效果越明顯。Khalili等人[8]建立了復合材料膠接修補結構的三維有限元模型，使用三維八節點實體單元模擬膠接接頭，探究了面內載荷作用下膠層的剪切應力和剝離應力的變化規律。韓允等人[9]采用“彈簧元”模擬膠層，建立了“雙板—彈簧元”有限元模型模擬分析了復合材料補片單面膠接修補含裂紋鋁合金板結構的應力分布狀況。

粘貼CFRP對鋼結構進行加固，膠層起著傳遞載荷的作用，鋼結構、膠層和CFRP的材料性能各異，膠層的受力狀態相當復雜，因此，研究膠層界面的應力分布對于分析膠層載荷傳遞機制以及結構失效破壞模式有著十分重要的指導作用。本文通過ANSYS有限元軟件模擬CFRP單面加固鋼板結構在拉伸載荷下的受力狀態，研究膠層的應力分布情況，并分析影響界面應力狀態的各項因素，為確定最優的加固修補方案提供理論依據。

1 有限元分析模型

1.1 基本假設

本文主要分析膠層的應力分布情況，采用二維分析模型就能夠獲得較高的計算精度，并且可以簡化模型、減少計算時間。為了保證模型的合理性，便于分析計算結果，作以下基本假設。

1)鋼板、CFRP和膠層的厚度與各自的面內尺寸相比很小，故三者均處于平面應變狀態，且均保持線彈性。

2)膠層為各向同性材料。

3)鋼板、CFRP和膠層初始膠接質量完好，粘接界面不發生脫膠現象。

4)忽略鋼板自重對膠層界面應力的影響。

1.2 有限元模型

CFRP單面加固鋼板結構的幾何尺寸如圖1所示，材料的力學參數如表1所示。本文利用ANSYS有限元軟件建立二維線彈性實體模型，CFRP、鋼板和膠層均采用平面單元PLANE182進行模擬，根據模型幾何結構和加載條件的對稱性，選取1/2模型進行建模分析，鋼板端部施加100 MPa均布載荷。

圖1 結構幾何尺寸

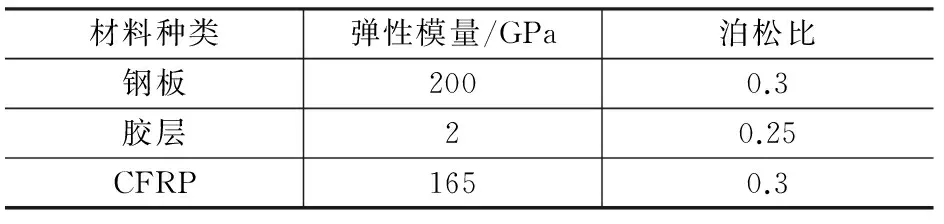
材料種類彈性模量/GPa泊松比鋼板2000.3膠層20.25CFRP1650.3

2 膠層應力分析

上述有限元模型計算出的膠層中面剪應力和正應力分布情況如圖2所示，有限元模擬結果與蘇維國[10]等人推導出的剪應力和剝離應力的解析解模型以及應力曲線分布規律相吻合，證明了本文有限元模型的正確性。從圖2可以看出，在CFRP和鋼板連接的自由端部附近，膠層的正應力和剪應力均發生突變，產生很大的波動，且剪應力和正應力的最大值均出現在該區域，說明在載荷作用下膠層端部存在明顯的應力集中現象。從圖2(a)中發現，離開CFRP端部一段距離后，剪應力逐漸減小，最后基本接近為零，通常把這段長度稱為CFRP的有限粘接長度，粘接剪應力主要存在于這一區域內。超出有效粘接長度之后，CFRP與鋼板之間幾乎不存在剪應力，CFRP的應變趨于穩定，不存在應變梯度，CFRP和鋼板已經開始處于共同受力狀態，即在有效粘接長度范圍之內，膠層已經完成了應力傳遞。

圖2(b)中Y向正應力又稱為剝離應力，從圖中曲線可以看出，在膠層端部剝離應力為拉應力，且存在拉應力最大值，隨著離開端部距離的增加，拉應力逐漸減小，然后變成壓應力，最后正應力基本接近于零。

從圖2(c)可以看出，X向正應力在膠層端部附近達到最大值，隨著距端部距離的增加，X向正應力先減小后增加，最后趨于平穩，整個過程中X向正應力均為拉應力。X向正應力產生的原因是由于鋼板和CFRP自身有變形，根據變形協調條件，膠層隨著鋼板和CFRP的應變而產生了自身的應變，從而產生了X向正應力。

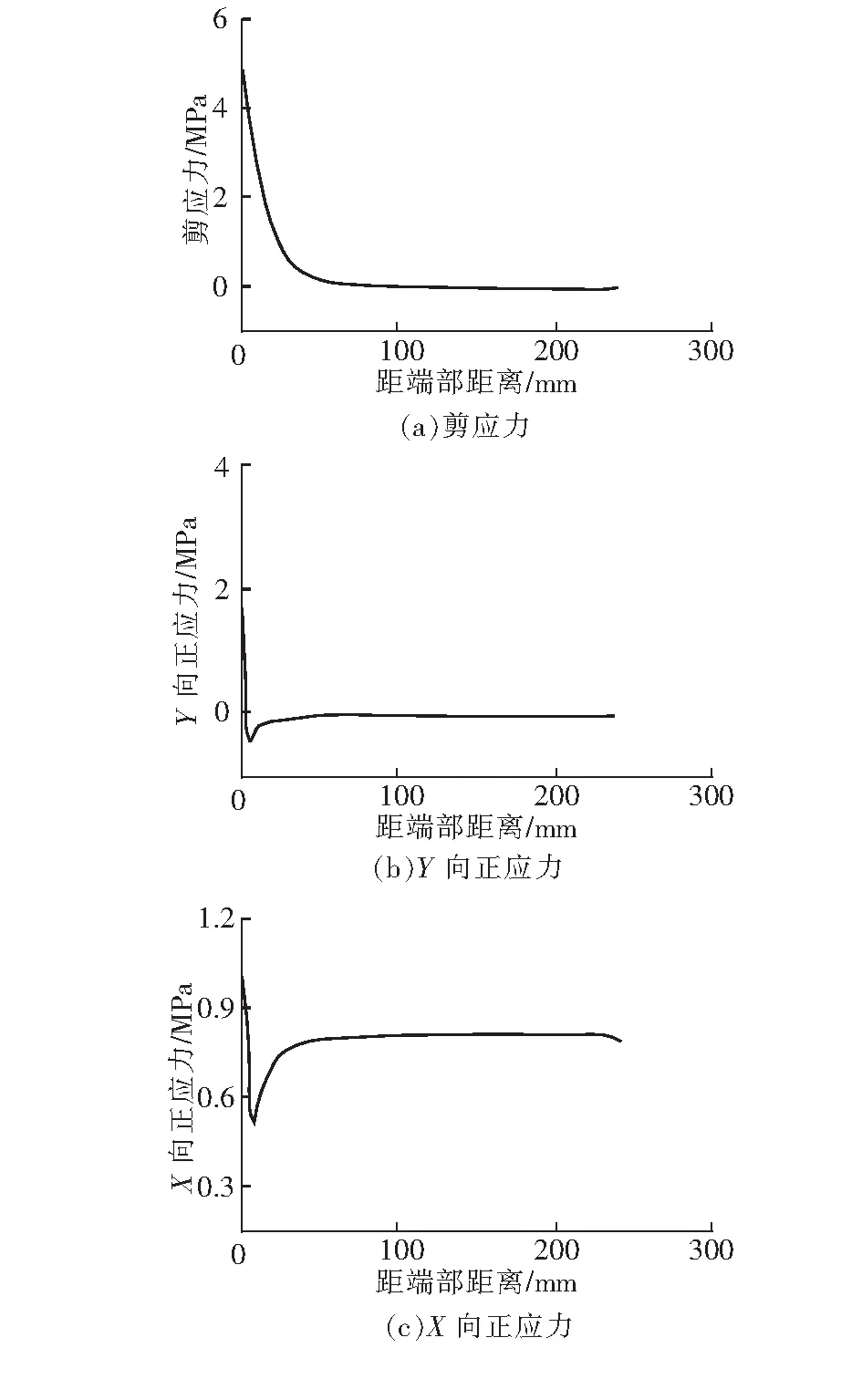
圖2 膠層應力分布圖

3 膠層應力值的影響因素

通過對單面加固結構的應力分析，獲得了膠層正應力和剪應力的分布規律，下面將研究CFRP和膠層的不同參數對膠層應力值的影響。

3.1 膠層彈性模量的影響

為研究膠層彈性模量對膠層應力值的影響，保持CFRP、鋼板和膠層的其他參數以及加載條件不變，設置膠層彈性模量分別為1 GPa、2 GPa、4 GPa、6 GPa的4組模型進行計算，4組模型膠層中面的剪應力和Y向正應力的對比情況如圖3所示。由計算結果可知，膠層的最大剪應力和最大Y向正應力均隨著膠層彈性模量的增加而增大。從圖3(a)的剪應力對比情況可以看出，當膠層的彈性模量從1 GPa增加到6 GPa后，最大剪應力從3.60 MPa增大到7.63 MPa，且膠層的有效粘接長度隨著膠層彈性模量的增大而減小。當膠層的彈性模量從1 GPa增加到6 GPa后，Y向拉應力最大值從2.20 MPa增大到7.20 MPa，壓應力絕對值最大值從0.29 MPa增大到1.03 MPa，說明膠層彈性模量越大，膠層端部的剪應力和剝離應力越大，膠層應力狀態更復雜，膠層更容易發生破壞導致失效。

圖3 膠層彈性模量對膠層應力的影響

3.2 膠層厚度的影響

在研究膠層厚度對膠層應力分布情況的影響時，保持鋼板和CFRP的參數不變，膠層的彈性模量和加載條件也保持一致，建立3組膠層厚度分別為0.5 mm、1 mm、1.5 mm的有限元模型進行計算，膠層應力對比情況如圖4所示。由計算結果可知，當膠層厚度從0.5 mm增加到1.0 mm時，Y向正應力最大值從4.90 MPa減小到3.52 MPa，減小了28.16%，剪應力最大值從6.76 MPa減小到4.85 MPa，減小了28.25%；當膠層厚度從1.0 mm增加到1.5 mm時，Y向正應力最大值從3.52 MPa減小到2.75 MPa，減小了21.88%，剪應力最大值從4.85 MPa減小到3.87 MPa，減小了20.21%，說明隨著膠層厚度的增加，膠層最大剪應力和最大剝離應力均有所減小。從圖4(a)的剪應力對比情況可以看出，膠層的有效粘接長度隨著膠層厚度的的增大而增加。因此，在保證單面加固粘接質量的前提下，適當地增加膠層厚度可以有效地降低加固構件產生脫粘失效破壞的可能性，提高加固效果。

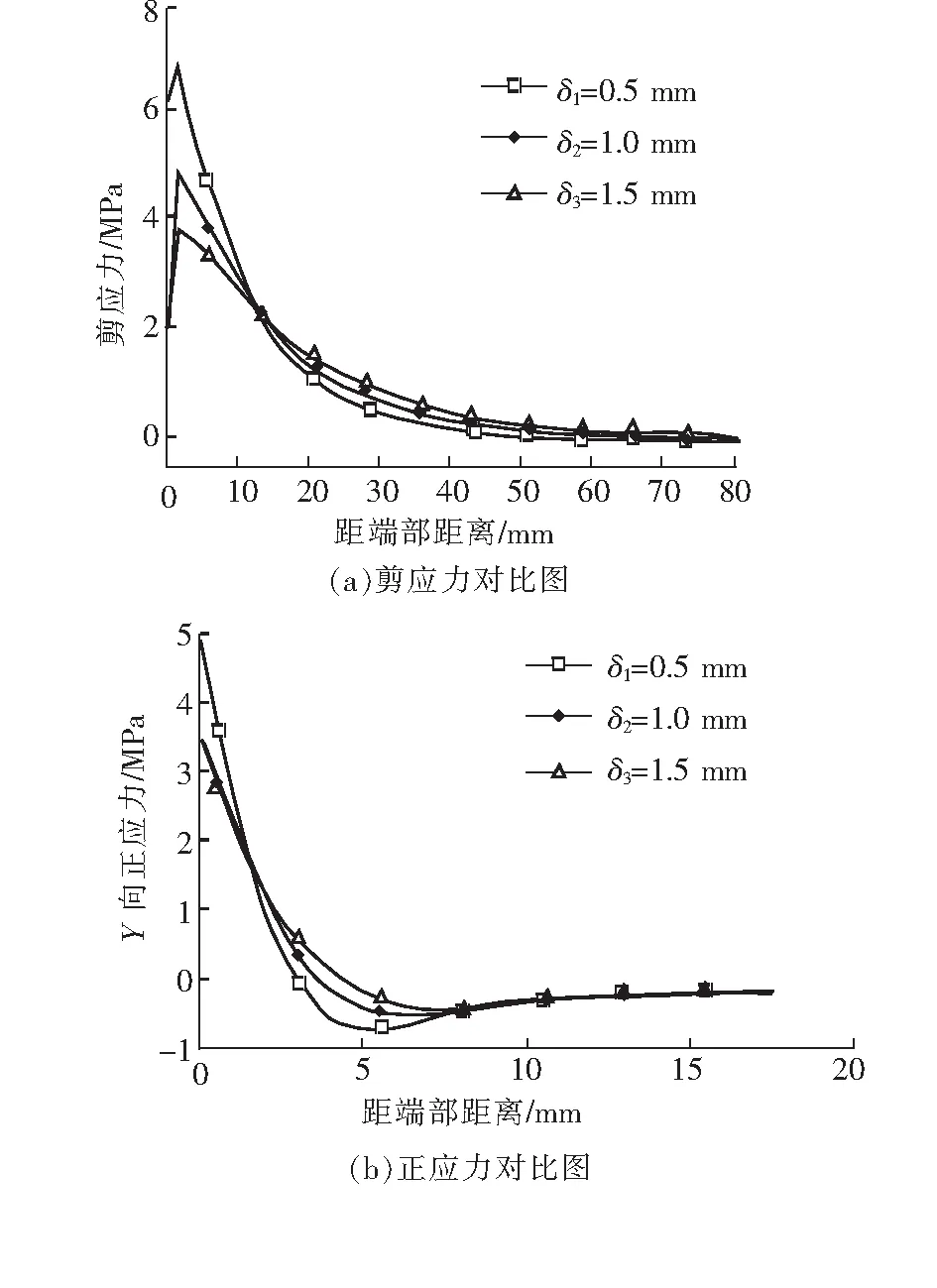
圖4 膠層厚度對膠層應力的影響

3.3 CFRP補片厚度的影響

在研究CFRP補片厚度對膠層應力的影響時，保持其他參數不變，設置CFRP補片厚度分別為0.5 mm、1.2 mm、2.0 mm、4.0 mm，在相同的均布載荷下進行有限元模擬計算，對比結果如圖5所示。從圖中可以看出，隨著CFRP補片厚度的增加，膠層端部的剪應力和剝離應力最大值都將增大，當CFRP補片厚度從0.5 mm增加到4.0 mm后，最大剪應力從3.22 MPa增加到7.18 MPa，剝離應力最大值從2.76 MPa增加到4.71 MPa，與此同時，補片越厚，CFRP的有效粘接長度越長。可見增加CFRP補片的厚度雖然使得膠層傳遞了更多的載荷，但同時也會加劇膠層本身發生失效破壞的風險。

圖5 CFRP厚度對膠層應力的影響

4 結束語

本文建立了CFRP單面加固鋼板的有限元模型，研究了膠層彈性模量、膠層厚度以及CFRP補片厚度對膠層應力的影響，分析結果如下。

1)CFRP單面加固鋼板時，在鋼板端部均布載荷的作用下，補片端部區域膠層的正應力和剪應力均存在明顯的應力集中現象，這是造成補片端部剝離的主要原因。

2)膠層的彈性模量越大，CFRP補片的厚度越大，膠層端部的剪應力和剝離應力越大，膠層的應力狀態更復雜，膠層本身更容易發生破壞。

3)隨著膠層厚度的增加，膠層最大剪應力和最大剝離應力均有所減小，但膠層太厚容易影響粘接質量，故適當地增加膠層厚度有利于提高加固效果。

[1] 馬建勛,宋松林,賴志生.粘貼碳纖維布加固鋼構件受拉承載力試驗研究[J].工業建筑,2003,33(2):1-4.

[2] 李耘宇,王言磊,歐進萍.FRP/鋼復合板單軸拉伸性能試驗研究[J].工業建筑,2013,43(S1):80-83.

[3] Colombi P, Poggi C. Strengthening of tensile steel members and bolted joints using adhesively bonded CFRP plates[J].Construction and Building Materials, 2006, 20(1-2):22-33.

[4] Bocciarelli M, Colombi P, Fava G, et al. Fatigue performance of tensile steel members strengthened with CFRP plates[J].Steel Construction, 2009,87(4):334-343.

[5]吳剛,劉海洋,吳智深,等.不同纖維增強復合材料加固鋼梁疲勞性能試驗研究[J].土木工程學報,2012,45(4):21-28.

[6]Jones S C, Civjan S A. Application of fiber reinforced polymer overlays to extend steel fatigue life[J].Journal of Composites for Construction,2003,7(4):331-338.

[7]鄭云,葉列平,岳清瑞,等.CFRP加固含疲勞裂紋鋼板的有限元參數分析[J].工業建筑,2006,36(6):99-103.

[8] Khalili S M R, Khalili S, Pirouzhashemi M R, et al. Numerical study of lap joints with composite adhesives and composite adherends subjected to in-plane and transverse loads[J].International Journal of Adhesion and Adhesives, 2008, 28(8): 411-418.

[9]韓允,劉元海,肖曉暉.復合材料膠接修補結構有限元分析方法研究[J].直升機技術,2016(3):32-35.

[10]蘇維國,穆志韜,朱做濤,等.金屬裂紋板復合材料單面膠接修補結構應力分析[J].復合材料學報,2014,31(3):772-780.

The strengthening method that steel construction reinforced with composite plates has several advantages and widespread engineering application,in which the key point lies in the fine interface performance between steel plate and composite plate.In order to investigate the mechanical properties of bonding interface and provide theoretical basis for the optimal reinforcement project,2D linear elastic FEM is built up to simulate the tensile test process and the interfacial stress of the adhesive layer between the steel plate and CFRP plate is studied through the finite element analysis program ANSYS.The parameters which influence the adhesive stress,such as the elastic modulus of adhesive,thickness of CFRP plate and thickness of adhesive,are studied by FEM in ANSYS.The analytical results indicate that the shear stress and peel stress on the free end of adhesive gradually increase with the increasing of the elastic modulus of adhesive and thickness of CFRP plate.It's helpfully to improve the reinforcing effect by increasing the thickness of adhesive layer appropriately.

composite;single-sided strengthening;adhesive stress;elastic modulus of adhesive;thickness of CFRP plate;thickness of adhesive

U672

10.13352/j.issn.1001-8328.2017.06.015

國家自然科學基金(51479206)

黃凌凱(1992-)，男，浙江蘭溪人，在讀碩士研究生，研究方向為復合材料有限元模擬。

2017-06-29