凸多邊形相似判定問題

唐樂紅

(福州陽光學(xué)院， 福建福州 350015)

凸多邊形相似判定問題

唐樂紅

(福州陽光學(xué)院， 福建福州 350015)

本文通過利用已有的秘密判定相等協(xié)議、 集合相等判定協(xié)議、 數(shù)據(jù)對應(yīng)成比例判定協(xié)議， 設(shè)計(jì)出凸多邊形相似判定協(xié)議， 并分析了其正確性、 安全性和復(fù)雜性.

計(jì)算幾何； 集合相等； 凸多邊形； 相似判定

0 引言

如果一個(gè)多邊形的所有邊中， 任意一條邊向兩方無限延長成為一條直線時(shí)， 其他各邊都在這條直線的同一側(cè)， 那么我們就稱這個(gè)多邊形為凸多邊形(邊數(shù)大于3). 生活中常見的正多邊形等都是凸多邊形. 判定兩個(gè)凸多邊形是否相似， 在數(shù)學(xué)、 物理等學(xué)科上都有很多的實(shí)際應(yīng)用.

本文假定雙方的計(jì)算環(huán)境是安全的， 且前提 是雙方都能嚴(yán)格遵守協(xié)議的規(guī)程. 在滿足以上條件的情況下， 利用秘密判定相等協(xié)議、 集合相等判定協(xié)議、 數(shù)據(jù)對應(yīng)成比例判定協(xié)議， 本文設(shè)計(jì)出凸多邊形相似判定協(xié)議.

1 基礎(chǔ)協(xié)議

1.1 秘密判定相等協(xié)議

兩個(gè)用戶希望在不向?qū)Ψ叫孤蹲约簲?shù)據(jù)信息的情況下， 比較出各自所持有數(shù)據(jù)是否相等. 如果雙方數(shù)據(jù)不相等時(shí)， 則要求任何一方都不能夠知道對方的數(shù)據(jù). 這就是秘密判定問題[1].

1.2 集合相等判定協(xié)議

兩個(gè)用戶各自擁有一個(gè)集合， 如何在不泄露雙方各自集合信息的情況下， 判定出兩個(gè)集合是否相等[2]， 這就是集合相等判定問題. 協(xié)議具體如下：

輸入： Alice擁有集合X={x1,…,xm},Bob擁有集合Y={y1,…,ym}.

輸出： 謂詞P(X,Y).

執(zhí)行過程：

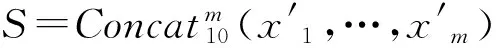
(3) Alice和Bob各自在本地利用商量好的散列函數(shù)， 計(jì)算出S′=hash(S)和T′=hash(T).