數(shù)學問題解答
2017-12-25 06:25:26
數(shù)學通報
2017年6期
2017年5月號問題解答
(解答由問題提供人給出)
2361若x,y,z是正實數(shù)，求證：
(1)
其中“∑”表示輪換對稱和.
(四川成都金牛西林巷18號華鑫園A601 宿曉陽 610031)
證明設y2+z2=a,z2+x2=b,x2+y2=c.則a,b,c為三角形的三邊.
于是(1)式等價于下列涉及三角形三邊的不等式
(2)
由柯西不等式，有
(3)
又由b2≥b2-(c-a)2,知
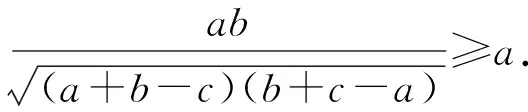
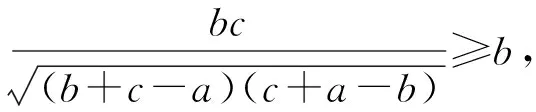
三式相加，得
(4)
(3)+2×(4)并開方，即得(2)式.故(1)式成立.
2362在△ABC中，a,b,c為其三邊長，ra,rb,rc與ha,hb,hc是其對應三邊上的旁切圓半徑與高，則有
(hb+hc)(hc+ha)(ha+hb)
(陜西省咸陽師范學院基礎教育課程研究中心 安振平 712000)
證明記△ABC的面積為S，注意到
應用正弦定理，以及三角恒等變形，得
三式疊乘，立即獲得
(hb+hc)(hc+ha)(ha+hb)
2363在△ABC中，AD、BE、CF相交于一點O，點D、E、F分別在△ABC三邊BC、CA、AB上，則有
min(AD,BE,CF) ≤OD+OE+OF
≤max(AD,BE,CF).
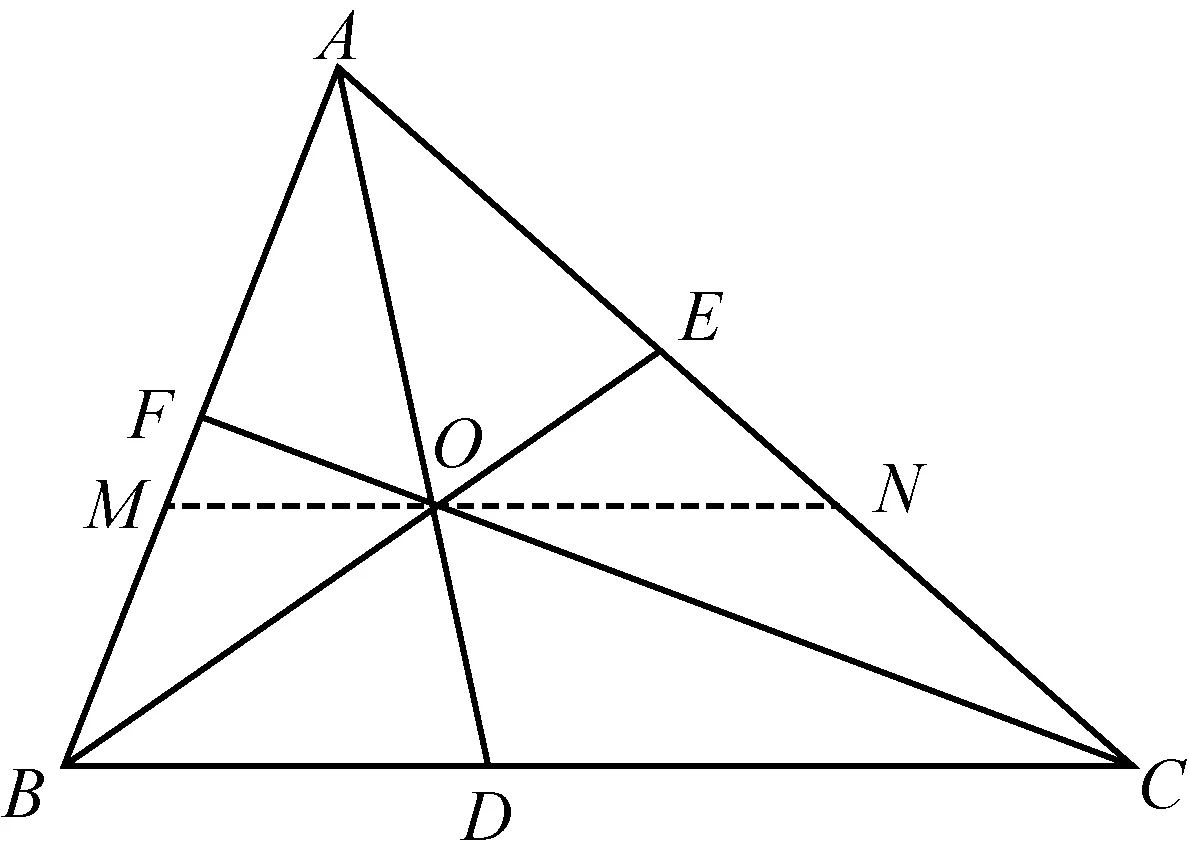
(西安衛(wèi)星測控中心 趙曉輝 714000)
證明不妨設AD≤BE≤CF，過O作直線MN平行于BC，交AB于M，交CA于N，則有
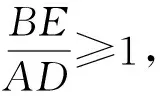
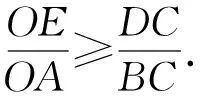
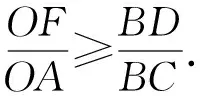
由此可得
即
OE+OF≥OA.
從而
OD+OE+OF≥OA+OD=AD.
類似可證
OE+OD≤OC,
得到
OD+OE+OF≤OC+OF=CF.
特別地，若AD=BE=CF，
則有OD+OE+OF=AD.
2364給定m≥3且m∈N，設a1,a2,…,am>0，n≥m且n∈N，求證：
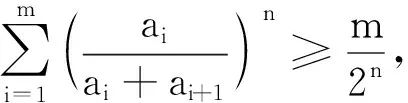
(湖南師大附中數(shù)學教研組 張湘君 410006)
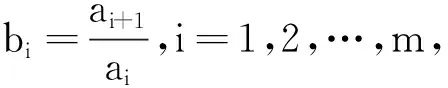
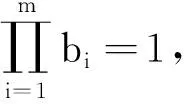
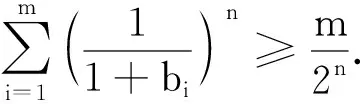
由冪平均不等式知
于是只需證明
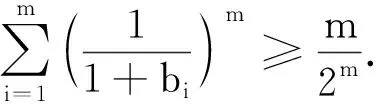
考慮到bi>0,i=1,2,…,m，
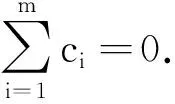
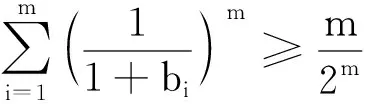
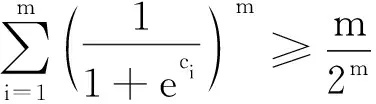
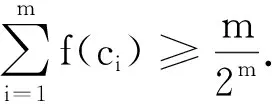
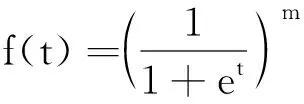
f″(t)=met(1+et)-m-2(met-1).
下面分兩種情況討論：
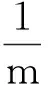
于是只需證明
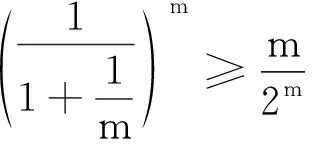
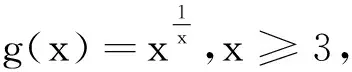
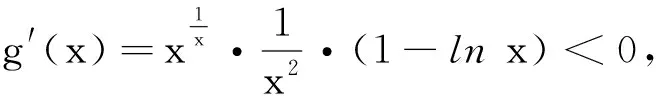
所以g(x)在x≥3時單調(diào)遞減，
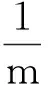
f″(t)≥0，則f(t)是下凸函數(shù)，
由琴生不等式得
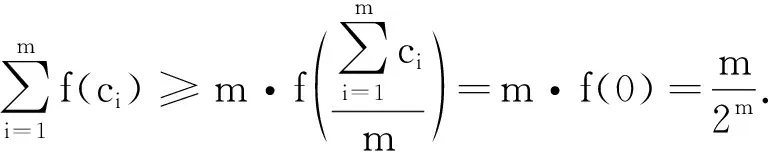
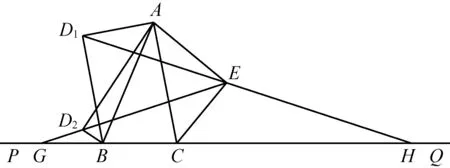
2365已知如圖，在△ABC中，點P、Q分別在CB、BC的延長線上，AE垂直于∠ACQ的平分線于點E，BD1、BD2在∠ABP的內(nèi)部，且∠ABD1=∠PBD2，AD1⊥BD1，AD2⊥BD2，直線D1E、D2E分別與直線PQ交于點H、G．
求證：△EGH為等腰三角形．
(北京市陳經(jīng)綸中學 張留杰 100020)
證明如圖，過點D1、D2作直線與PQ交于點F，
因為 ∠AD1B=∠AD2B=90°，
所以A、D1、D2、B四點共圓，
且這個圓是以AB為直徑.
設圓心為O，則O為AB的中點，
所以 ∠BD2F=∠BAD1．
因為∠BAD1+∠ABD1=90°，
又∠ABD1=∠FBD2，
所以∠BD2F+∠FBD2=90°，
所以∠BFD2=90°，即D1D2⊥BC．
延長AE交PQ于R點，
因為CE平分∠ACQ，AE⊥EC，
所以易得△ACE≌△RCE，
所以AE=ER，即點E是AR的中點．
連結(jié)EO并延長交D1D2于M，
因為OE是△ABR的中位線，
所以EO∥PQ，所以EO⊥D1D2，
由圓中的垂徑定理可得M是D1D2的中點，
所以易得Rt△EMD1≌Rt△EMD2，
所以∠D1EM=∠D2EM．
又∠D1EM=∠EHG，∠MED2=∠EGH，
所以∠EGH=∠EHG，
所以△EGH為等腰三角形．
