非線性思維觀下的圖案設計及應用

唐 穎,陳楚婷

(江南大學 紡織服裝學院,無錫 江蘇214122)

非線性思維觀下的圖案設計及應用

唐 穎,陳楚婷

(江南大學 紡織服裝學院,無錫 江蘇214122)

通過分析非線性思維及非線性圖形的定義和特點,提出了基于非線性思維的圖案設計方法,并延伸至實際設計及應用;同時結合非線性思維理論及原理探討了在實際設計過程中發現的問題和應用成果。

非線性思維;分形理論;圖案設計

1 非線性思維觀

1.1 非線性思維的定義

非線性是當今科學界的前沿與熱點,涉及自然科學、人文社會科學和哲學等眾多領域。它在20世紀60年代興起,雖其概念、性質至今仍在發掘之中,但無疑已經影響了人們的思維方式,改變了人們對世界的認識,在當今眾多前沿學科的研究中發揮了重要的作用[1]。非線性思維方式在藝術設計領域也逐漸滲透進來,尤其在建筑設計、景觀設計等方面已經出現了一些實踐非線性思維的設計案例[2-3]。非線性思維中時空觀念的轉變,以及對自然界復雜事物自組織規律、審美原理的揭示,為藝術設計的現代發展注入了新的空氣。非線性思維廣義來說就是與常規的線性思維不一樣的思維方式,看問題的邏輯與角度相對于線性思維而言沒有那么多慣性和常理。非線性思維是一種相互作用、無限制、無邊界、非單一立體化或平面化的交織結構,類似于植物的根莖與葉脈。而線性思維可能只是單一的、同一維度的、不多變的。

在非線性思維系統中,變化及變量是不可估摸的,它很有可能因為當中的某一個微小的因素改變整個形勢的現狀,而無從知曉形勢發生變化的源頭。相對于許多線性思維看問題時需要通過大量以往的經驗和信息的分析形成的慣性思維,具有很大的局限性和不可變性的。非線性思維的未知性較強,所呈現相關的內容的拓展性和可變性也更強。用非線性思維的角度看問題能更全面更深入地了解問題的本質,也能使人們更加客觀地去看待許多問題。非線性思維實際上包含了線性思維,非線性思維無處不在,但大多數情況下人們由于思維局限、思維慣性而將其以線性思維去理解和感受,從而使非線性思維這一概念,在藝術設計領域還是比較陌生。

1.2 非線性圖案的定義

非線性圖案是運用非線性理論或非線性思維方式產生的圖形,非線性圖案并不單一由直線或者曲線構成,也不需要通過線條的組合及排列而形成千變萬化的圖案,可理解為一種多維狀態的圖形,這一點與線性圖形是有所區別的。同時,它還具有一定的數學特性和物理特性,也可通過數據運算、函數公式輸出等,加入計算機編程語言軟件的輔助或將數據直接輸入特定的軟件當中,所輸入的內容將以圖形的形式呈現在熒幕上。

2 非線性思維設計方法

在展開設計之前,將設計思路分為幾點:一是目前關于非線性思維的圖案其實并不多見,希望在傳統的圖案設計方向上,加入非線性的思維,從而發掘并總結出一些非線性圖案的特征及特點;二是從收集的圖案資料中截取部分元素對其進行設計,其難點關鍵在于設計過程如何保持非線性圖案的特點,同時又具有獨特的審美風格;三是對于現有的圖案形式通過解構、重組、倒序等手段加以創新。

2.1 突破性——打破傳統與形式美法則的新式設計理念

從以往對于圖案設計的經驗來看,大多數設計師的靈感來源于線性思維,對于美好的事物潛意識中將其具象化或線象化,常采用勾線法和色彩平涂法進行圖案設計并且十分注重圖案的連續性和完整性。而非線性思維觀希望能打破這一傳統的設計慣性,通過不同的表現手法、立體團內部空間的扭曲等等營造圖案從固定形態到動態美感這一審美形式的轉變。其實在非線性理論中存在很多現象,如混沌、頻率與振幅的關系、分諧波振蕩、多值響應等。換而言之,在線性理論中是很難得到這些奇怪的現象,比如在線性函數中,當X軸數值發生改變,隨之Y軸必定會隨之變化,這種變化是單一的、同一平面內的;而若在非線性函數中,將一個數值帶入其中可能會使得整個函數現象發生多種形式的變動,而這種變動是多向的,甚至有可能延伸至整個空間,產生多維度的變化。正是種種的不確定因素造就了非線性的“標新立異”,這種“標新立異”也是非線性思維奇妙之處。對比傳統圖案設計,是需要以“標新立異”的思維進行創新和設計的,若能將非線性思維融入到設計中,就算基礎圖案是一條簡單的直線或者四方形,在非線性思維中它是有無限種可能性的,可對簡單圖形組織、變換,形成新的圖形,甚至形成立體圖案。

同時,在傳統的圖案設計中形式美法被十分看重,希望通過圖形直接的沖撞重疊,打破平衡感,營造出“不完整”的視錯效果,使得圖案在視覺效果上得到新的開發。

2.2 自相似性——從生活中尋找靈感再歸于生活

自相似性這一特點最初是在非線性思維中一個分支——分形理論中發現的。分形的概念最初是由美國著名數學家本華·曼德博提出的,在他1967年發表的著名論文《英國的海岸線有多長?統計自相似和分數維度》中提到:英國的海岸線長度是無法確定的,在測量過程中它存在的變量太多,而單純依賴于測量的尺度是無法將其精準測量出來的。簡單來說,由于大大小小的島嶼及海峽輪廓有著數以萬計的變化,所以在可視范圍內,我們無法很清楚地將其局部形態和整體形態很好地區分完整,但它們之間是具有自相似性的。而類似這種整體與局部之間具有一定的相似性但又有所區別,可以理解為分形[4]。實際上,分形理論就是非線性理論的一個分支,它的自相似性、不完整性等都與非線性理論中的概念十分接近。淺顯一點來理解,它與相似有一定字面上的相同,而在實際中是不一樣的,所謂自相似性,是圖像與圖像直接具有相似之處,無論整體圖像是如何變化,其內部圖像之間總是保持著一定的自相似性。但自相似性又不能簡單地理解為某一個圖像和某一個圖像一樣,它們只是處于一個相似的狀態下,同時具有自己的特征[5]。生活中隨處可見分形的蹤影,如鐵銹、干裂的土地、葉片、扎染圖案、刺繡等,可見分形是一種非常貼近人們生活的概念,而圖案設計本身也是服務于生活,因此更應該注重對其的理解和運用。

2.3 整體性——運用非線性思維把握整體與局部的關系

整體性的簡單概念是圖案無論從整體上看還是局部上看,它都是具有美感的,盡管遵循不完整原則,但一定要把握住整體與局部的關系。參考現有的部分非線性圖案設計,發現容易出現的問題是在局部過于繁雜導致形成整體圖案時便顯得累贅。在非線性的概念中,其中的變量會引起無窮大的變化,但這種變量是關系到整個圖像的,簡單來說就是它小的變量形成的影響是一整個部分的而不是單一存在的。無論是服裝設計還是家紡設計,都會注重作品的系列感,所謂的系列感即整體視覺上的感受,所以整體性在此就顯得尤為重要了。而當前圖案設計中的系列普遍來說都是簡單的復制、組合,并沒有過多的組織或者完善,在設計圖稿的過程中,能做到的就是將設計的思路連成一個整體,設計的風格、種類可以是多樣化的,但每一個系列設計中必須注重的就是整體性。不僅考慮到結果,還要注重過程,這是非線性蘊含的又一思維方式,根據這一點也有助形成系列化圖案。

同時,為了使得圖案不局限于某類服飾或紡織品的應用,嘗試在應用中盡量拓展圖案的使用率,而為了能擴大使用范圍,在設計圖案時就要考慮到圖案的可延伸性,所設計的圖案必然是具有一定可塑性和可轉換性的,這也是非線性整體思維的體現。

3 非線性思維設計實例分析

在設計的過程中,想法和創意是最重要,經過對非線性的分析及設計思路的整理,總結了非線性圖案具有其自身特性[6]。如不完整、破碎、無限性、自相似性等,這些特性的發現為之后的設計提供了很大的幫助,將這些特有的性質相互交織,融會貫通,最終成功實現一系列的設計方案。

3.1 病原體系列

病原體系列圖案設計的靈感源泉是基于分形理論,但并不同于一般數理運算形成的分形圖案。許多非線性函數中,分形本身就是一種會隨著數據變動而產生不同節奏和韻律的無規則、無限定的圖形。在傳統的圖案設計中,十分注重圖案之間的構成感,比如形式美法則中的對稱、統一、對比等,很多時候都成為人們評判一幅設計作品好壞的準則。病原體是細菌、病毒、寄生蟲、真菌等可造成生物感染疾病的微生物的統稱。大多數病原體在一定條件下是會自我進行培養和繁殖的,而在繁殖過程中不斷地分裂、破碎、結合成新的病原體。這一生物特性和分形幾何及混沌力學中提到的打破、重構等概念十分類似,而在設計成果(圖1)中可以發現,繪制圖案時并沒有單獨將某一種元素過多地重復或相互對應,而是從整體上所有的內容都是相映得彰,環環相扣的,這是對于傳統圖案設計概念的一種打破和沖擊,同時又成功將分形圖案的自相似性,局部與整體相呼應的特性表現出來。在圖案的細節處理上,放棄了傳統圖案的講究和嚴謹,將細菌、真菌等復雜難以表達的元素簡單化,再通過彼此之間的聯系以及巧妙的布局,使得設計稿在不經意間被完整,富有獨特的韻律和張力。

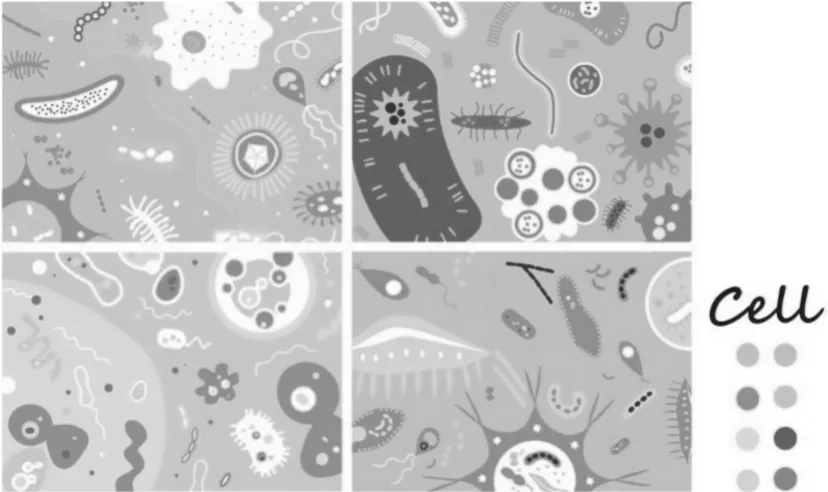
圖1 病原體系列圖案設計

3.2 萬花筒系列

萬花筒作為一種利用物理光反射原理的玩具,將不同形態的實物放于圓筒底部,通過窺孔即可看到其形成的特殊鏡像圖形。這種對稱圖形會隨著圓筒的轉動而源源不斷地形成許多有趣的圖像,是抽象而又千變萬化的,具有非線性圖案的特征。這種圖像的形成并不由單一的點、線、面組成,而是互相交替產生的,所以若單獨將成像結果截取出來,人們很難根據成像猜到原始物體的全部,這給予人們很大的空間去想象,拓展了人們的思維,產生了趣味之處。

在設計該系列的初始階段使用了手機軟件對物體做萬花筒效果處理,發現簡單地將物體以萬花筒的形式展現并不能使用且形成的圖像十分粗糙。但大量的拍攝工作和圖像截取為設計提供了靈感及元素,因此從中選取部分的圖像用繪圖軟件將設計元素規整化,從而形成圖案,如圖2所示。與其他系列的區別在于萬花筒系列圖案中遵循了萬花筒與傳統圖案共有的特性——四方連續性。其原因在于使得圖案能被更廣泛地運用在不同的產品當中;且在于由于萬花筒特性所致,形成的圖案容易繁雜花哨,四方連續的形式可使保證在不失去圖案原本隨意性的情況下保持圖案完整性,即趨于整體又不失局部,體現了非線性思維中整體與局部之間的關系。

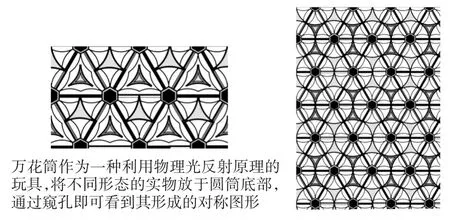
圖2 萬花筒系列圖案設計

4 設計圖案應用實例

在設計應用時,選擇將細菌系列圖案作品與女童裝相結合(圖3)。在童裝日常服飾設計中,衣服易穿脫性十分重要,這是為兒童在沒有成年人輔助的情況下也能自行穿脫為出發點作為考慮,因此款式設計上我們沒有運用太復雜的服裝結構,主要以基本款為主:連帽衛衣、蓬蓬裙、針織外套、背帶褲、T恤以及連衣裙等。也正因為款式較為簡單,因此我們選擇了色彩較豐富且具有趣味性的病原體系列圖案,這樣不僅能讓款式看上去沒有那么普通,而且趣味性的圖案能使人產生愉悅的心情,并且符合孩童活力青春的可愛形象,比市場上常見的卡通形象或日常的印花圖案更能打動消費者。

圖3 病原體系列圖案在女童服裝設計中的應用

5 結語

自然界的非線性特征中隱藏著十分龐大的靈感源泉,不是通過簡單的概念性分析和設 計就能將其把握的。圖案設計案例所使用的設計靈感元素的病原體、萬花筒等都是生活中十分常見而不起眼的“小東西”,但往往這樣不起眼的“小東西”卻蘊含了很豐富的變化和獨特的美感。如何用非線性這一思維去看待問題,在有限的范圍內對生活進行無限的思考,就如同非線性思維一樣具有無窮的探索空間,從而能夠創造出更多美好的事物。

[1] 李潤珍,武 杰.非線性提供了一種新的思維方式[J].科學技術與辯證法,2003,20(2).26-29.

[2] 龔曉文.非線性思維及其在建筑中的應用研究[D].長沙:湖南大學,2008.

[3] 匡 緯.基于非線性思維觀的景觀設計策略研究[D].北京:北京林業大學,2011.

[4] 桑莉君.現代設計中的分形藝術研究[D].太原:太原理工大學,2015.

[5] 代沛涵.分形圖案在紡織紋樣設計上的應用[D].蘇州:蘇州大學,2015.

[6] 唐 穎,房寬峻,沈 雷.分形圖案與傳統紡織印花圖案的形式美感對比[J].紡織學報,2009,30(12):90-94.

Pattern Design and Application under the View of Nonlinear Thinking

TANG Ying,CHEN Chu-ting
(School of Textiles and Clothing,Jiangnan University,Wuxi 214122,China)

Definition and characteristics of nonlinear thinking and nonlinear-graph were analyzed,pattern design based on nonlinear thinking and its practical design and application were proposed.At the same time,combined with the theory and principle of nonlinear thinking,problems and application results in actual design process were discussed.

non-linear thinking;fractal theory;pattern design

TS941.2

A

1673-0356(2017)12-0042-03

2017-10-25

國家自然科學基金青年科學基金項目(61503154);江蘇省研究生教育教學改革研究與實踐課題(JGLX16_047);江南大學本科教育教學改革研究一般項目(JG2015041)

唐 穎(1983-),女,湖南永州人,博士,副教授,主要研究方向為服裝設計與品牌,E-mail:9984874@qq.com。