環(huán)Z2+uZ2+u2Z2(u3=1)上的2-D斜循環(huán)碼
趙瑞瑞,李秀麗
(青島科技大學(xué)數(shù)理學(xué)院,山東 青島 266061)
環(huán)Z2+uZ2+u2Z2(u3=1)上的2-D斜循環(huán)碼
趙瑞瑞,李秀麗*
(青島科技大學(xué)數(shù)理學(xué)院,山東 青島 266061)
本文研究了環(huán)Z2+uZ2+u2Z2上的2-D斜循環(huán)碼,對二元斜多項式的性質(zhì)和因式分解進(jìn)行了討論。同時研究了線性碼是2-D斜循環(huán)碼的充要條件、2-D斜循環(huán)碼的性質(zhì)及其構(gòu)造方法 。
斜循環(huán)碼;斜多項式;2-D斜循環(huán)碼
1 預(yù)備知識
多項式環(huán)和理想通常被用來構(gòu)造循環(huán)碼。斜多項式環(huán)是非交換環(huán),在代數(shù)碼的構(gòu)造上應(yīng)用廣泛。因為斜多項式環(huán)中的多項式不滿足乘法交換律,因此斜多項式環(huán)中比多項式環(huán)中存在更多的理想。文獻(xiàn)[1-2]中提出了利用斜多項式來構(gòu)造循環(huán)碼的一種推廣形式——斜循環(huán)碼,并且構(gòu)造出了許多好碼。近幾年,編碼領(lǐng)域的科學(xué)工作者以高斯環(huán)、Z2+uZ2+u2Z2、F4+vF4、Fp+vFp作為主要的研究對象,在斜循環(huán)碼的構(gòu)造方面,文獻(xiàn)[1-6]做了很多卓有成效的工作。文獻(xiàn)[3]中討論了環(huán)Z2+uZ2+u2Z2上的斜循環(huán)碼與多項式環(huán)理想的關(guān)系,并給出了斜循環(huán)碼的生成多項式。文獻(xiàn)[7]中介紹了在有限域上二維斜循環(huán)碼的一些基本性質(zhì)和構(gòu)造方法,以及2-D斜循環(huán)碼和斜循環(huán)碼以及循環(huán)碼之間的關(guān)系。
在本文中環(huán)R=Z2+uZ2+u2Z2={0,1,u,u2,1+u,1+u2,u+u2,1+u+u2},其中u3=1。對任意的兩個元素a=a0+ua1+u2a2,b=b0+ub1+u2b2∈R,定義加法規(guī)則如下:c=a+b=c0+uc1+u2c2,其中ci=ai+bi(mod 2),i=0,1,2。乘法定義為c=ab=c0+uc1+u2c2,其中c0=a0b0+a1b2+a2b1(mod 2),c1=a0b1+a1b0+a2b2(mod 2),c2=a0b2+a2b0+a1b1(mod 2)。

c=(c0,c1,…,cn-1)∈C?Τσ(c)=(σ(cn-1),σ(c0),…,σ(cn-2,))∈C,
映射Τσ稱為σ-斜移位算子。如果σ是單位映射,那么C是R上的循環(huán)碼。
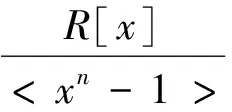
設(shè)σ是R上的一個自同構(gòu)映射,多項式集合R[x,σ]={∑aixi|ai∈R;i∈Z+}。在R[x,σ]上加法運(yùn)算定義為普通多項式加法,乘法定義為axi·bxj=aσi(b)xi+j。由分配律和結(jié)合律可擴(kuò)充為R[x,σ]上的任意元素之間的運(yùn)算,因此R[x,σ]是一個環(huán) 。
通常,如果f(x)∈R[x,σ]生成一個雙邊理想,那么R[x,σ]/
設(shè)σ和θ是R上的兩個自同構(gòu)映射,二元多項式集合
R[x,y;σ,θ]={∑∑aijxiyj|aij∈R;(i,j)∈Z+2},
在R[x,y;σ,θ]上加法運(yùn)算定義為普通多項式加法,乘法定義如下:
axiyj·bxryt=aσiθj(b)xi+ryj+t,
由分配律和結(jié)合律可擴(kuò)充為R[x,y;σ,θ]上的任意元素之間的運(yùn)算,因此R[x,y;σ,θ]是一個環(huán)。
定義1.2 設(shè)C是一個在R[x,y;σ,θ]上長度為n的線性碼,n=sl,寫成矩陣的形式,?c∈C有
如果矩陣c的行在σ斜移位和列在θ斜移位下仍在C中,稱C是一個R上的在σ和θ下大小為sl的2-D斜循環(huán)碼。如果σ和θ是單位映射,C是2-D循環(huán)碼。
2 二元斜多項式環(huán)R[x,y;σ,θ]
設(shè)f,g∈R[x,y;σ,θ],且f,g的最高次項的系數(shù)在R上可逆,如果存在h∈R有f=h·g,那么g稱為f的右因子。左因子的定義類似。若g與任意多項式可交換,則g(x,y)∈Z(R[x,y;σ,θ]),稱g為中心多項式。
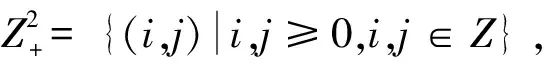
與[5]中證明類似,可得到以下結(jié)論:
引理2.1 如果g·h∈Z(R[x,y;σ,θ]),那么g·h=h·g。即一個中心多項式的右因子也是它的左因子。
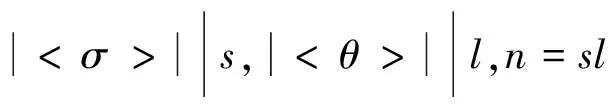

(xs-1)·f(x,y)=f(x,y)·(xs-1)和(yl-1)·f(x,y)=f(x,y)·(yl-1)。
證明:設(shè)f(x,y)∈∑∑ai,jxiyj,ai,j∈R,
另一等式同理可證。
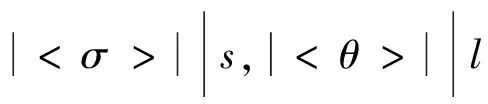
下面將文獻(xiàn)[4]中定理1推廣到到二元斜多項式環(huán)。
定理2.3 設(shè)兩個非零多項式f1(x,y),f2(x,y)∈R[x,y;σ,θ],滿足deg(f1(x,y))≥deg(f2(x,y)),那么存在兩個多項式h(x,y)≠0,g(x,y)∈R[x,y;σ,θ]滿足f1(x,y)=h(x,y)·f2(x,y)+g(x,y)有h(x,y)=0或deg(f2(x,y))!≤deg(g(x,y))deg(f1(x,y))。(其中!≤表示不嚴(yán)格小于)
證明:設(shè)deg(f1(x,y))=(k1,λ1),deg(f2(x,y))=(k2,λ2)滿足(k1,λ1)≥(k2,λ2)。假如f1(x,y)和f2(x,y)的最高次項分別為ak1λ1xk1yλ1和bk2λ2xk2yλ2,ak1,λ1≠0且bk2λ2≠0,在R上可逆,存在h1(x,y)=ak1λ1(σk1-k2θλ1-λ2)-1(bk2λ2)xk1-k2yλ1-λ2和g1(x,y)=f1(x,y)-h1(x,y)·f2(x,y),顯然有g(shù)1(x,y)=0或deg(g1(x,y))deg(f1(x,y))。如果g1(x,y)≠0,deg(f2(x,y))!≤deg(g1(x,y))結(jié)論得證,否則deg(f2)≤deg(g1)。類似地,存在h2(x,y)和g2(x,y)有g(shù)1(x,y)=h2(x,y)·f2(x,y)+g2(x,y),滿足g2(x,y)=0或deg(g2(x,y))deg(g1(x,y))。如果g2(x,y)≠0,deg(f2(x,y))!≤deg(g2(x,y)),結(jié)論得證,否則deg(f2)≤deg(g2)。繼續(xù)按上述方法迭代,在有限次運(yùn)算之后停止,我們得到h1(x,y),h2(x,y),…,ht-1(x,y)和g1(x,y),g2(x,y),…,gt(x,y)有
f1(x,y)=h1(x,y)·f2(x,y)+g1(x,y),
g1(x,y)=h2(x,y)·f2(x,y)+g2(x,y),
…,
gt-1(x,y)=ht(x,y)·f2(x,y)+gt(x,y),
滿足gt(x,y)=0或f2(x,y)!≤gt(x,y)。如果gt(x,y)≠0,有
deg(gt(x,y))deg(gt-1(x,y))…deg(g1(x,y))deg(f1(x,y))。
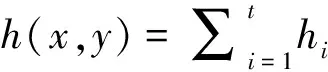
例2.4 設(shè)f1(x,y)=x4y2-2xy+5,f2(x,y)=x2y-2x+2,滿足deg(f1(x,y))>deg(f2(x,y)),容易得出f1(x,y)=h(x,y)·f2(x,y)+g(x,y),其中h(x,y)=x2y-2,g(x,y)=-xy-2x+9,滿足定理要求。
3 2-D斜循環(huán)碼的結(jié)構(gòu)
且l是滿足上述條件的最小正整數(shù)。
這意味著,在R上長為n=sl下標(biāo)為l的斜準(zhǔn)循環(huán)碼C是在映射Τσ,l下Rsl的不變的R-子模。
設(shè)C是R上的長為n=sl的線性碼,它的碼字可以寫成s×l的矩陣形式:
從定義中可知C是2-D斜循環(huán)碼的充要條件是:
①C1是一個在σ下長為sl指數(shù)為l的斜準(zhǔn)循環(huán)碼;
②C2是一個在θ下長為sl指數(shù)為s的斜準(zhǔn)循環(huán)碼。
設(shè)F=R[x,y;σ,θ]/
Rs×l→F,
Rs×l記為s×l的矩陣的集合。那么一個碼字c∈C可以被記為在上述映射下的一個二元多項式。因此在R上的斜循環(huán)碼也可以認(rèn)為是F的左R[x,y;σ,θ]-子模。
定理3.2F上的碼C是一個2-D斜循環(huán)碼,當(dāng)且僅當(dāng)C是一個F的左R[x,y;σ,θ]-子模。
證明: “?”在F中的碼C是2-D斜循環(huán)碼,碼C中的任意碼字的行σ-移位和列θ-移位仍在C中。設(shè)f(x,y)是C中的碼字的二元多項式表示,對任何非負(fù)整數(shù)i,j{xiyjf(x,y)}R仍是C中碼字的二元多項式表示,{xiyjf(x,y)}R表示x的指數(shù)模s,y的指數(shù)模l。C是線性的有{r(x,y)f(x,y)}R∈F,對?f(x,y)∈R[x,y;σ,θ],所以C是F的左R[x,y;σ,θ]-子模。
“?”設(shè)C是F的左R[x,y;σ,θ]-子模,那么對?f(x,y)∈F我們有{x·f(x,y)}R∈C,{y·f(x,y)}R∈C。因此C是一個2-D斜循環(huán)碼。
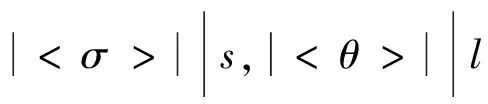

例3.4 取R上的自同構(gòu)映射σ、θ為:σ(a0+ua1+u2a2)=a0+u2a1+ua2,其中ai∈Zi,i=0,1,2,σ=θ。易知若a∈R,則θ2(a)=a,即θ的階為2。 設(shè)l=4,s=2,那么D=
理想D有一個生成元為xiyj(x2+uxy+u2x2y)模
4 結(jié)語
本文對2-D斜多項式環(huán)的性質(zhì)和因式分解進(jìn)行了討論,給出了環(huán)Z2+uZ2+u2Z2上的一個自同構(gòu),討論了其上的2-D斜循環(huán)碼的性質(zhì)及其構(gòu)造,并給出了一個實例加以說明。由于Z2+uZ2+u2Z2上的斜循環(huán)碼是廣義斜循環(huán)碼,其個數(shù)要比循環(huán)碼多,因此研究斜循環(huán)碼有利于找到更多的好碼。
[1]BOUCHERD, GEISELMANN W, ULMER F. Skew cyclic code[J].Applied Algebra in Engineering Communication and Computing,2007,18(4): 379-389.
[2]BOUCHER.,ULMER F. Coding with skew polynomial rings [J].Journal of Symbolic Computation,2009, 44: 1644-1656.
[3]李錦,朱士信.Z2+uZ2+u2Z2上的斜循環(huán)碼[J].合肥工業(yè)大學(xué)學(xué)報(自然科學(xué)版),2011,34(11):1745-1748.
[4]徐賢奇,朱士信.F4+vF4上的斜循環(huán)碼[J].合肥工業(yè)大學(xué)學(xué)報(自然科學(xué)版),2011, 34(9):1429-1732.
[5]BHAINTWAL M. Skew quasi-cyclic codes over Galois rings[J]. Des Codes Cryptogr,2012,62: 85-101.
[6]ABUALRUB T, GHRAYEB A, AYDIN N , et al. On the construction of skew quasi-cyclic codes [J]. IEEE Transactions on Information Theory, 2010, 56: 2081-2090.
[7]LIX L, LI H Y. 2-Dskew-cyclic codes overFq[x,y;ρ,θ][J]. Finite Fields and Their Applications, 2014,25:49-63.
2-DskewcycliccodesovertheringZ2+uZ2+u2Z2(u3=1)
ZHAORui-rui,LIXiu-li*
(SchoolofMathematicsandPhysics,QingdaoUniversityofScienceandTechnology,Qingdao266061,China)
∶In this paper, the2-Dskew cyclic codes over the ringZ2+uZ2+u2Z2was studied. The properties and factorizations of bivariate skew polynomial were also discussed. Then the necessary and sufficient condition for linear code to be 2-Dskew cyclic code were given. Finally,the properties and the structure of 2-Dskew cyclic code were researched.
∶skew cyclic codes; skew polynomial;2-Dskew cyclic codes
10.3976/j.issn.1002-4026.2017.06.020
2017-01-09
山東省中青年科學(xué)家獎勵基金(BS2011DX011);山東省科技廳聯(lián)合專項(ZR2013AL011)
趙瑞瑞(1992—),男,碩士研究生,研究方向為組合設(shè)計編碼。
*通信作者,李秀麗,女,副教授,碩士生導(dǎo)師,研究方向為組合設(shè)計編碼。1436354481@qq.com
O157
A
1002-4026(2017)06-0119-05

