福州特高壓變電站短路電流分流系數計算與分析

，， (中國電力工程顧問集團西南電力設計院有限公司，四川 成都 610021)

福州特高壓變電站短路電流分流系數計算與分析

楊凌霜，鄒家勇，余波
(中國電力工程顧問集團西南電力設計院有限公司，四川 成都 610021)

變電站內發生短路故障時真正引起危害的是入地故障電流，而不是短路故障電流。分流系數表征了接地網或架空地線對故障電流的分流能力，可用于分析短路電流的分布情況。研究了變電站站內故障時短路電流的分流機制，提出了適用于工程實際的分流系數定義，重點介紹了分流系數的數值計算方法。在此基礎上計算了福州特高壓變電站的分流系數與短路入地電流，并分析了分流系數的各種影響因素。分析結果表明：地線分流系數隨著變電站接地電阻的增大而增大，隨著桿塔接地電阻的增大而減小；500 kV側和1 000 kV側短路時地線分流系數差別較小；隨著變電站接地電阻的增大，最大入地電流減小，接地電壓增大。

變電站站內短路；分流系數；接地電阻；短路電流；接地電壓

0 引 言

變電站良好的接地是電力系統安全運行的根本保證。電力系統短路故障一般分為變電站站內短路和站外短路兩種類型。與站外短路相比，站內短路對變電站安全運行危害更大，更容易引起事故。因此這里主要研究變電站站內短路故障[1]。

變電站內部短路故障電流可分為地線分流、變壓器中性點回流和入地電流三部分，真正產生嚴重危害、危及人身和設備安全的是入地故障電流。根據GB/T 50065-2011《交流電氣裝置的接地設計規范》的規定[2]，變電站接地系統設計時不僅需要校核短路電流的大小，還需要分析系統短路分流情況，從而準確計算短路入地電流，為接地網設計提供依據[3]。

變電站接地系統的分流系數是指入地故障電流與短路故障電流的比值。分流系數的合理選擇是變電站接地系統設計的基礎，直接關系到變電站的安全運行[4]。變電站分流系數與短路故障的類型和位置、系統的結構與參數、變電站和桿塔接地電阻、相線和架空地線參數等多種因素有關，精確計算分流系數非常困難。目前獲得分流系數的方法主要有經驗公式法和數值計算法，經驗公式法模型簡單但計算精度較低[5]，數值計算法考慮模型相對復雜，計算結果較為準確[6]。因此下面重點介紹分流系數的數值計算方法。

1 計算條件

所研究的變電站為福州特高壓GIS變電站，1 000 kV側有兩回進線，都為單回線路，分別為浙南1線和浙南2線；500 kV側有四回進線，都為同塔雙回線路，分別為笠里1線、笠里2線、寧德1線和寧德2線。變電站內運行主變壓器有兩臺，都是三相自耦變壓器。變電站及線路參數如表1、表2、表3所示。

表1 主變壓器參數

表2 導線參數

表3 地線參數

2 分流系數的計算方法

2.1 變電站站內短路電流分析

由于輸電線路的架空地線和變電站接地網連為一體，短路故障電流從接地網入地時，一部分電流會通過變電站的地線從桿塔的接地裝置和遠端變電站入地。入地電流與總故障電流的比值(分流系數)受變電站接地電阻、線路地線電阻、桿塔接地電阻等的影響比較大。此外，架空地線與相導線之間的互感也會起很大作用。實際變電站發生短路故障時，故障電流由線路的相導線提供，即相導線作為電流引線，如圖1所示。

由于相導線與地線保持長距離平行且二者之間的距離非常近，這會產生很大的線路互感。相導線提供的故障電流會通過互感的作用在地線中感應出很大的反向電流，這部分電流是分走故障電流的主要部分之一。對于多回輸電線路，由于互感的作用，提供故障電流多的線路地線分走的電流多，其他線路地線分走的電流少；同時，地線電阻和桿塔接地電阻也會對分流起到一定作用。

圖1 變電站站內故障電流路徑

圖2為變電站站內故障的等值電路[7]，圖中：ZGi為架空地線的零序自阻抗；ZLi為導線的零序自阻抗；ZMi為導線和架空地線間的零序互阻抗；Ri為輸電線路桿塔的接地電阻；R為變電站接地電阻；RT為終端電站的接地電阻；V為發生短路故障前的電壓源。為簡便起見，圖中給出的每檔線路參數采用相同的標識，分析時可以根據實際情況將各接地電阻及阻抗采用不同的值。

圖2 變電站內短路故障時的等效電路

變電站站內短路時，電流分布如圖3所示[8]。短路故障電流為I0(工程設計中經常會提供該電流)，該電流是由變壓器兩側的無窮遠端的電源提供的(無窮遠端的電源未出現在圖3中)，而不僅僅來自于短路側的電源。根據基爾霍夫定律，這些短路電流終將流回兩側的電源。由于是站內短路，因此部分電流Ig會直接通過接地系統由大地流向無窮遠端的電源。由于變壓器中性點和線路地線都連接在地網上，因此也有部分電流通過變壓器中性點(有時也包含發電機的中性點)和高低壓側線路地線流出接地網，即IN、Iw1和Iw2。對于通過地線流回電源的電流Iw1和Iw2，在逐級經過桿塔時又會有部分電流通過桿塔接地系統流向大地，即Iw12和Iw22，剩余電流Iw11和Iw21則繼續通過地線流回電源。

2.2 站內故障的分流系數

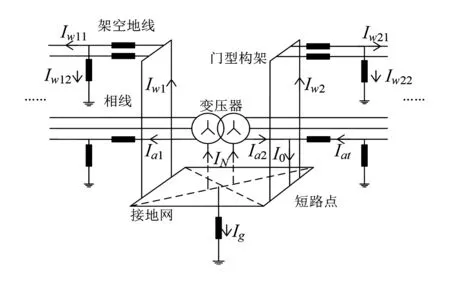
圖3 變電站站內短路情況下的電流分布

由2.1節變電站站內短路電流的分流情況可以引出分流系數的定義。分流系數可以分為接地網的分流系數和地線的分流系數兩個方面，分別表征變電站發生站內短路故障時，接地網和架空地線對短路故障電流的分流能力。

IEEE標準[5]和國家標準[2]中通常給出的是地線的分流系數Ksl，可表示為

(1)

式中，Iw為所有流經地線的短路電流的總和。相應地，接地網的分流系數Ksg可表示為

(2)

在實際工程中，真正引起危害、帶來安全問題的是入地故障電流Ig。接地系統接地電阻的安全閾值由入地故障電流Ig決定；接地電壓、網孔電壓、接觸電壓、跨步電壓等也與入地故障電流成正比[9]：因此主要關注入地故障電流Ig及其對應的分流系數Ksg。

由于工程設計中經常提供短路故障電流I0，一般不提供通過變壓器中性點電流IN，并且IN的計算比較復雜。因此為了方便設計人員使用，研究中的入地電流分流系數與前述標準規定不同，直接定義Ig/I0為接地網的分流系數。

2.3 分流系數計算原理

數值計算是分流系數最準確的計算方法，即建立接地系統、輸電線路、架空地線等電氣元件的等值電路，然后利用電磁暫態分析程序進行求解。文獻[10]考慮了耦合因素和線路的互阻抗，采用集中參數等值電路計算分流系數。文獻[11]提出了串級矩陣法，即將每個線路檔距的阻抗矩陣串聯起來，該方法能考慮所有的自阻抗、互阻抗和故障類型及位置。文獻[12]提出了一種用簡單方程組求解接地網及桿塔電流的方法。文獻[13]采用圖解法求得了分流系數與接地電阻等參數的一系列關系曲線，可以根據這些曲線方便地得到分流系數。

電力系統短路電流計算可分為序分量法和相分量法[14-15]。考慮線路換位、架空地線接地、各導線間互感等實際情況，故障條件下各相電量之間的關系是不對稱的。因此，正序、負序、零序分量存在相互耦合，此時不能采用傳統的序分量法進行求解。相分量法對各相導線、架空地線和電纜外皮等線路參數沒有對稱條件的約束，因此運用相參數較為直觀，也更為精確。求解相參數電路可以歸結為基本的電路求解問題。

電力系統所有元件都可以用廣義導納矩陣進行模擬[16]，因此可以將每個元件表示為

Ik=YkVk-bk(k=1,2,…,n)

(3)

式中:Ik為元件終端電流向量；Vk為元件終端的電壓向量；Yk為元件的廣義導納矩陣；bk為獨立電流源向量。式(3)的節點方程形式為

YV=b

(4)

式中:Y為由各元件的導納矩陣組成的整個系統的導納矩陣；V為各節點的電壓向量矩陣；b為由各電流源構成的獨立電流源，對于輸電線路模型b= 0。

對式(4)進行修改即可模擬故障時的情況。如果在節點i和節點j之間發生故障，則應在故障Y的Yi, i和Yj, j元素中加上故障導納Yf，在Yi, j和Yj, i元素中減去故障導納Yf。求解式(4)的方程即可得到各節點的電壓，代入式(3)可得到電流分布。

將導納矩陣進行分塊則能快速求解所需的電流，得到分流系數。包括故障電流在內的節點方程為

YNV=bN+I

(5)

式中:YN為整個系統的無故障元件的導納矩陣；bN為整個系統無故障元件的獨立電流源向量；I為系統與故障元件接口處的電流向量。

系統中的元件可分為故障連接元件和其他元件兩部分，因此可以將式(5)分解為

(6)

式中:下標1表示與故障元件相連接的元件；下標2表示系統其余元件；I1為與故障元件相連接的系統終端處的電流向量。式(6)可以轉換為

YeV1=be+I1

(7)

式中:Ye為除了故障元件外的整個系統的等效導納矩陣，be為等效獨立電流源，即

(8)

(9)

通過這種轉換可以將多元件系統等效為一個元件。在此基礎上可以求出接地系統的接地電壓和從變電站接地網流入大地的電流，進而計算分流系數。

3 福州站分流系數與短路入地電流計算

變電站內部發生短路時，其分流系數是由系統中的電流分布決定的，因而其中影響分流系數的相關參數如下：變電站接地網的接地電阻、桿塔接地裝置的接地電阻、地線自阻抗、相線自阻抗、相線和地線間的互阻抗以及從母線看入系統的等值阻抗。變電站和桿塔的接地電阻是影響分流系數的重要因素，研究中作為主要變化參數進行分析。

3.1 福州站分流系數計算

由于線路桿塔接地電阻可能有變化，將線路桿塔接地電阻分別取10 Ω、15 Ω、25 Ω和35 Ω，計算不同變電站接地電阻下，不同短路側的短路電流分布和分流系數，結果如表4至表7所示。

表4 桿塔接地電阻為10 Ω時地線分流系數

圖4 桿塔接地電阻為10 Ω時地線分流系數

由圖4可見，隨著變電站接地電阻的增大，500 kV側和1 000 kV側的地線分流系數基本呈線性增長，且1 000 kV側的分流系數略大于500 kV側。

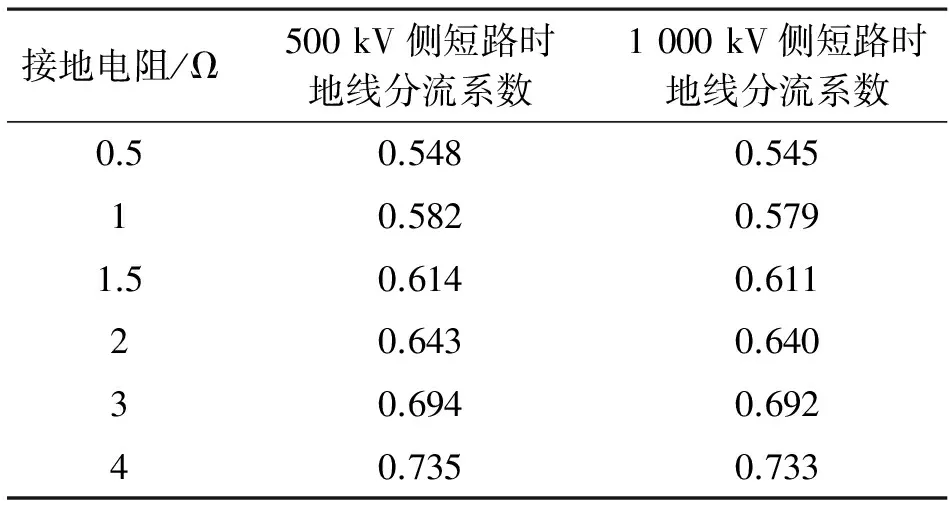
表5 桿塔接地電阻為15 Ω時地線分流系數

表6 桿塔接地電阻為25 Ω時地線分流系數

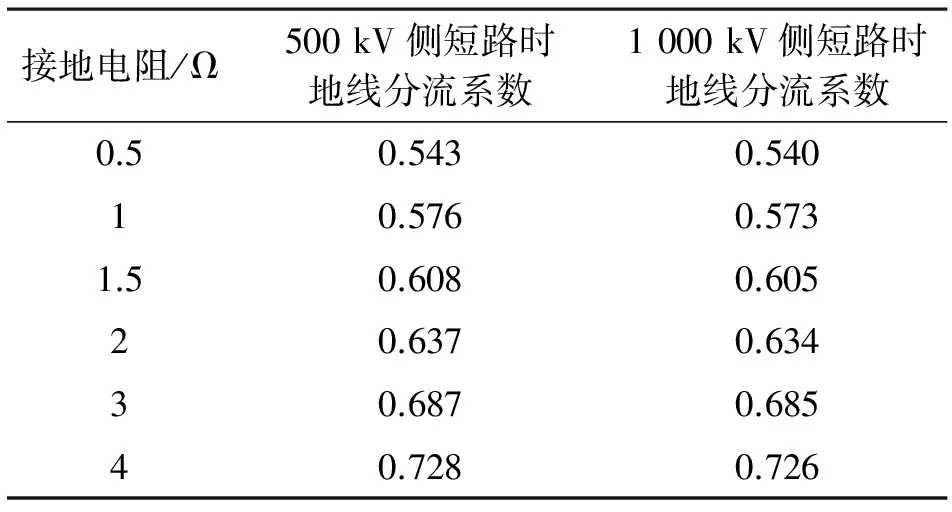
表7 桿塔接地電阻為35 Ω時地線分流系數

圖5 變電站接地電阻為0.5 Ω時地線分流系數

由計算結果可以看出，隨著變電站接地電阻的增加，地線分流系數逐漸增大(0.55～0.75)；而從圖5可以看出，隨著桿塔接地電阻的增加，地線分流系數逐漸減小，但變化不大(0.550～0.544,500 kV側；0.547～0.540，1 000 kV側)。500 kV側短路和1 000 kV側短路時的地線分流系數差別較小。

3.2 福州站短路入地電流計算

考慮最普遍的單相短路情況進行計算，1 000 kV側單相短路電流為24.1 kA，500 kV側單相短路電流為57.19 kA。由于500 kV側短路和1 000 kV側短路時的地線分流系數差別不大，則考慮最危險情況，應使用500 kV側單相短路電流57.19 kA分析實際最大入地電流，且地線分流系數為桿塔接地電阻10 Ω時的結果，短路入地電流計算結果如表8所示。

表8 變電站短路入地電流隨接地電阻的變化

圖6 變電站短路入地電流隨接地電阻的變化

由圖6可見，隨著變電站接地電阻的增大，短路最大入地電流逐漸減小，而接地電壓則逐漸增大，且這兩種變化趨勢逐漸趨于平緩。因此，在實際工程變電站接地系統設計中，不能只關注分流系數(最大入地電流)，必須同時考慮接地電阻對接地電壓的影響，對變電站進行合理的降阻設計，有效降低接地電壓，從而提高變電站安全性。

4 結 論

前面系統地研究了變電站站內故障時短路電流的分布和分流系數的計算，并給出了適用于工程實際的變電站分流系數的定義。在此基礎上介紹了分流系數數值計算方法中經典的矩陣法。基于以上理論分析，以福州特高壓GIS變電站為例，計算了福州站發生站內短路故障時的分流系數、短路入地電流和接地電壓，分析了變電站分流系數的多種影響因素。結果表明：

1)變電站分流系數由系統中的電流分布決定。影響分流系數的因素有變電站接地網的接地電阻、桿塔接地裝置的接地電阻、地線自阻抗、相線自阻抗以及架空地線的電氣參數等。

2)變電站和桿塔的接地電阻是分流系數的重要影響因素，地線分流系數隨著變電站接地電阻的增大而增大，隨著桿塔接地電阻的增大而減小。500 kV側和1 000 kV側短路時地線分流系數差別較小。

3)隨著變電站接地電阻的增加，最大入地電流明顯減小，接地電壓卻逐漸增大，且這兩種相反的變化趨勢逐漸趨于飽和。因此有必要對變電站進行合理的降阻設計。

[1] 何金良，曾嶸．電力系統接地技術[M]．北京：科學出版社，2007．

[2] 中國電力企業聯合會．GB 50065-2011，交流電氣裝置的接地設計規范[S]．北京：中國計劃出版社，2011．

[3] 曹煒，王永生，張文青，等．電力系統短路電流直流分量及其對短路器開斷能力的影響[J]．電網技術，2012，36(3)：283-288．

[4] 李謙，蔣愉寬，肖磊石，等．變電站內短路電流分流系數實測和分析[J]．電網技術，2013，37(7)：2060-2065．

[5] Substations Committee of the IEEE Power Engineering Society．IEEE Guide for Safety of AC Substation Groundings[S]．New York，USA：IEEE，2000．

[6] 何金良，張波，曾嶸，等．1 000 kV特高壓變電站接地系統的設計[J]．中國電機工程學報，2009，29(7)：7-12．

[7] 文習山，胡建平，唐炬．復雜電力網絡短路電流分布及地網分流系數[J]．高電壓技術，2011，37(9)：2233-2240．

[8] 吳錦鵬，張波，蔣愉寬，等．基于相分量模型的變電站短路電流分流系數計算[J]．中國電機工程學報，2012，32(1)：122-130．

[9] 陸家榆，龐廷智，薛辰東，等．城區變電站地電位模擬測試研究[J]．電網技術，2004，28(14)：57-61．

[10] Endrenyi J．Analysis of Transmission Tower Potentials during Ground Faults [J]．IEEE Transactions on Power Apparatus and Systems，1967，86(5)：1274-1283．[11] Sebo S A．Zero-sequence Current Distribution along Transmission Lines [J]．IEEE Transactions on Power Apparatus and Systems，1969，88(3)：910-919．

[12] Dawalibi F．Ground Fault Current Distribution between Soil and Neutral Conductors [J]．IEEE Transactions on Power Apparatus and Systems，1980，99(2)：452-461．

[13] Garrett D L，Myers J G，Patel S G．Determination of Maximum Substation Grounding System Fault Current Using Graphical Analysis [J]．IEEE Transactions on Power Delivery，1987，2(3)：725-732．

[14] 姜彤，白雪峰，郭志忠，等．基于對稱分量模型的電力系統短路故障計算方法[J]．中國電機工程學報，2003，23(2)：50-53．

[15] 黃銳峰，李琳．新的基于相分量的變壓器模型及其在統一廣義雙側消去法中的應用[J]．中國電機工程學報，2004，24(7)：188-193．

[16] Meliopoulos A P, Webb R P,Joy E B, et al.Computation of Maximum Earth Current in Substation Switchyards[J].IEEE Transactions on Power Apparatus and Systems,1983,102(9):3131-3139.

When a short-circuit fault occurs in a substation, it is the current diffusing into ground that actually causes the safety trouble instead of the fault current. Shunt coefficient characterizes the shunt ability of grounding grid or overhead ground wires to fault current, so it can be used to analyze the distribution of short-circuit current. The shunt mechanism of short-circuit current is studied when a fault occurs in substation, a definition of shunt coefficient that is more suitable for engineering practice is proposed, and the numerical computation method of shunt coefficient is introduced. On this basis, the shunt coefficient and current diffusing into ground of Fuzhou 1 000 kV substation are calculated, and various factors affecting the shunt coefficient are analyzed. The results show that shunt coefficient of ground wire increases with the increase of substation grounding resistance and decreases with the increase of tower grounding resistance, the differences of shunt coefficient of ground wires is tiny when short-circuit fault occurs in 500 kV side and 1 000 kV side. With the increase of substation grounding resistance, the current diffusing into ground decreases and the ground potential rise increases.

short-circuit fault in substation; shunt coefficient; grounding resistance; short-circuit current; grounding voltage

TM74

A

1003-6954(2017)05-0022-05

楊凌霜(1990)，助理工程師、碩士，主要研究方向為變電站接地技術；

鄒家勇(1982)，高級工程師、碩士，主要研究方向為變電站接地技術、電磁場理論。

2017-06-27)