混凝土材料高壓狀態方程研究
嚴 巋
(福建璟榕工程建設發展有限公司,福建 福州 350000)
混凝土材料高壓狀態方程研究
嚴 巋
(福建璟榕工程建設發展有限公司,福建 福州 350000)
通過混凝土的HugoniotD—U曲線推導出P—U曲線,采用實例分析得出體積壓力P與體應變v之間的關系式,并按照多項式的Grüneisen方程形式擬合出了高壓狀態方程參數,這對防護工程領域有著非同一般的意義。
Hugoniot,防護工程,Grüneisen方程
1 概述
目前,隨著建筑的需求,混凝土的抗沖擊特性越來越重要,在爆炸荷載和武器等的作用下,防護結構處于GPa級甚至更大的高壓狀態時,混凝土可當作為無粘性可壓縮的流體[1-5],其本構方程就是靜水壓力與體積應變之間的關系,即高壓狀態方程。高壓狀態方程是沖擊動力學的重要組成部分,如何通過試驗得到高壓狀態方程的參數,在防護工程領域有著非同一般的意義,本文通過一級氣體炮的沖擊壓縮實驗數據,從混凝土拉格朗日分析出發,研究混凝土高壓狀態方程。
2 混凝土材料高壓狀態方程描述
高壓狀態方程最常用的方法是基于混凝土的一級氣體炮高速沖擊壓縮實驗數據,研究了混凝土沖擊絕熱關系。通過混凝土的HugoniotD—U曲線推導出P—U曲線,采用實例分析得出體積壓力P與體應變v之間的關系式,并按照多項式的Grüneisen方程形式擬合出了高壓狀態方程參數。下面對該方法進行討論。
實驗中常常采用對稱碰撞,也就是同種混凝土材料的高速碰撞,每次輸入飛片的速度u1,得到沖擊波后的粒子速度為:
U=1/2u1。
根據一組飛片u1和沖擊波速度D(由兩個位置的位移與相差的時間決定),絕大部分密實介質的沖擊波速度D與質點速度U是線性關系:
D=a+bU。
通過試驗數據點可以擬合得到a與b的值。
而沖擊波壓力P與質點速度U有下列關系:
P=ρDU=ρ(a+bU)U。
從而得到P—UHugoniot曲線。
采用文獻[5][6]中的試驗結果,擬合得到D—U曲線見圖1,通過計算得到圖2。
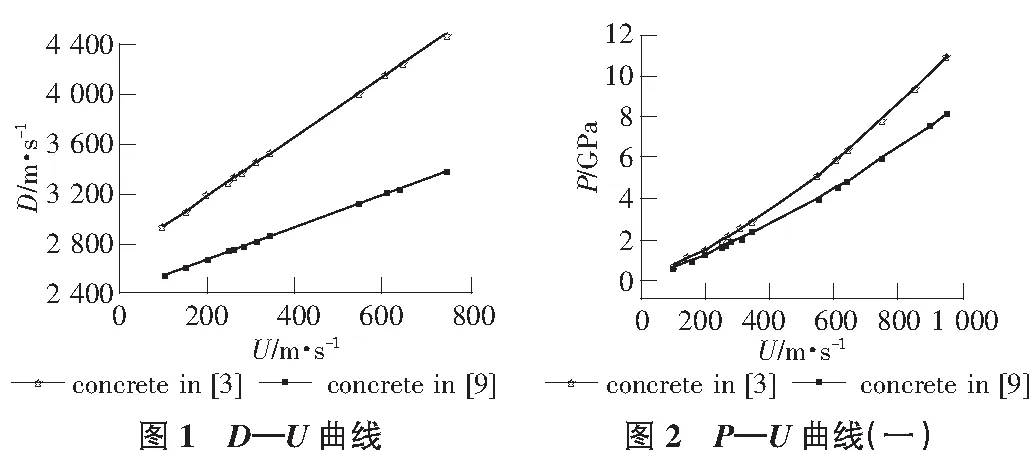
將上式代入質量守恒方程:
ρ1(D1-U)=ρ2(D2-U)。
得到:
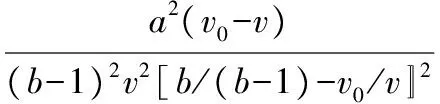


為了表明方法的可行性,將計算出的C30混凝土P—U曲線與文獻[6]進行對比如圖3所示,從圖3可以看出,本文理論計算結果與文獻數據基本接近。
上面的方法求解過程雖然理論性強,但是計算比較復雜,一般為了簡化計算,混凝土材料的容變律通常采用多項式形式的Grüneisen型狀態方程來描述,其方程具體形式為:
P=A1U+A2U2+A3U3。
其中,A1,A2,A3均為擬合系數。
通過對圖1,圖2的擬合得到了C30混凝土的高壓狀態方程參數:A1=19.09,A2=-156.26,A3=999.655。3個參數代入上式即為C30混凝土完整的高壓狀態方程。
3 結語
基于混凝土的一級氣體炮高速沖擊壓縮實驗數據,研究了混凝土沖擊絕熱關系。通過混凝土的HugoniotD—U曲線推導出P—U曲線,采用實例分析得出體積壓力P與體應變v之間的關系式,并按照多項式的Grüneisen方程形式擬合出了高壓狀態方程參數,這將大大的推動建筑結構抗沖擊動力學性能研究。
[1] 嚴少華,錢七虎,周早生,等.高強混凝土及鋼纖維高強混凝土高壓狀態方程的實驗研究[J].解放軍理工大學學報(自然科學版),2000,1(6):49-53.
[2] 陳 克,黃德武,劉 焜,等.基于MCA方法研究高速沖擊下混凝土高壓狀態方程[J].彈箭與制導學報,2008,28(6):123-125.
[3] 黃瑞源.混凝土類材料的含損傷動靜態力學行為和抗侵徹性能研究[D].合肥:中國科學技術大學,2013.
[4] 陳廷君.沖擊作用下混凝土性能的二維數值模擬[J].電力學報,2010,25(2):174-176.
[5] 張鳳國.動載荷作用下混凝土靶板損傷破壞的數值分析[J].兵工學報,2009,30(9):1177-1180.
[6] 王永剛,張遠平,王禮立,等.C30混凝土沖擊絕熱關系和Grüneisen型狀態方程的實驗研究[J].物理學報,2008,57(12):7789-7793.
Studyonhighpressureequationofstateforconcretematerials
YanKui
(FujianJingrongEngineeringConstructionDevelopmentCo.,Ltd,Fuzhou350000,China)
TheP—Ucurve is derived HugoniotD—Ucurve of concrete. The relation between the volume of the pressurevand volume strainPis obtained by the analysis of examples. According to the Grüneisen equation, the parameters of high pressure equation of state is presented fitting polynomial which is of unusual significance for protection engineering field.
Hugoniot, protection project, Grüneisen equation
2017-10-09
嚴 巋(1968- ),男,工程師
1009-6825(2017)35-0118-02
TU502
A

