一類連續(xù)型單參數(shù)指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes雙側(cè)檢驗(yàn)

黃金超

（滁州職業(yè)技術(shù)學(xué)院 基礎(chǔ)部，安徽 滁州 239000）

0 引言

單參數(shù)指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes（EB）檢驗(yàn)問題,在以往文獻(xiàn)中已有非常多的研究，如文獻(xiàn)[1-7]等對其做了不同程度的研究，并取得有意義的結(jié)果，彭家龍等[8]在“線性損失”下研究了一類連續(xù)型單參數(shù)指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes單側(cè)檢驗(yàn)，但是目前幾乎所有研究單參數(shù)指數(shù)族EB檢驗(yàn)問題的文獻(xiàn)，都是利用密度函數(shù)的普通核估計(jì)來構(gòu)造參數(shù)的EB檢驗(yàn)。本文將在“平方損失”下利用密度函數(shù)的遞歸核估計(jì)來研究一類廣義單參數(shù)指數(shù)族參數(shù)的經(jīng)EB雙側(cè)檢驗(yàn)問題。本文采用“平方損失”和遞歸核估計(jì)，研究參數(shù)的雙側(cè)檢驗(yàn)。

設(shè)隨機(jī)變量X條件概率密度[8]：

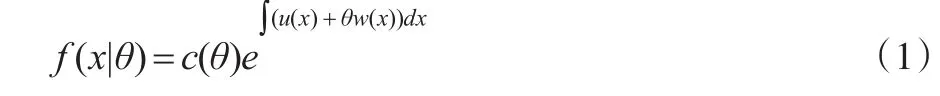
這里u（x）和w（x）為連續(xù)函數(shù)，不妨設(shè)u（x）＞0和 w（x）＜0，樣本空間為參數(shù)空間為

本文考慮分布族式（1）中參數(shù)θ的如下EB雙側(cè)檢驗(yàn)：

此處θ1和θ2為已知正常數(shù)，若取和則雙側(cè)檢驗(yàn)式（2）等價(jià)于：

對假設(shè)檢驗(yàn)式（3），取下列“平方損失”函數(shù)為：

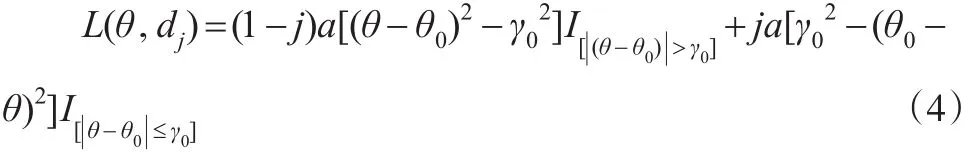
δ（x）=P（接受H0|X=x） （5）

為隨機(jī)化判別函數(shù)，則在先驗(yàn)分布 G（θ）下 δ（x）的Bayes風(fēng)險(xiǎn)函數(shù)為：

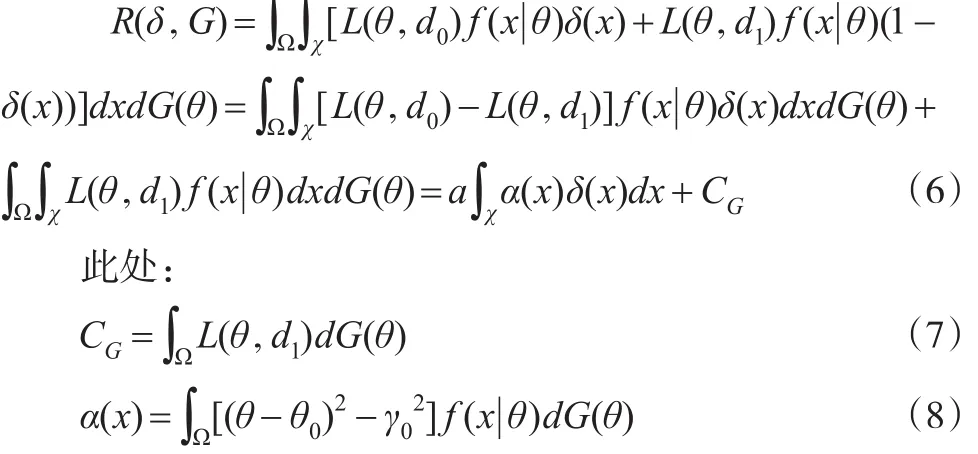
其中：

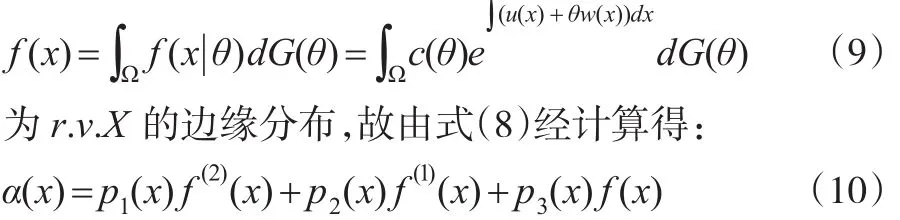
其中 f（1）（x），f（2）（x）分別表示 f（x）的一階，二階導(dǎo)數(shù)，且：

由式（6）易見Bayes判決函數(shù)為：

其Bayes風(fēng)險(xiǎn)為：

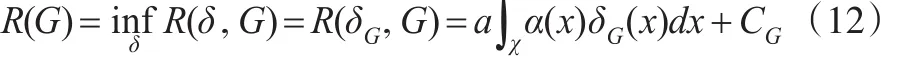
上述風(fēng)險(xiǎn)當(dāng) G（θ）已知，且 δ（x）=δG（x）是可以精確達(dá)到的，但此處G（θ）未知，因而 δG（x）不能使用，于是考慮引入EB方法。

1 EB檢驗(yàn)函數(shù)的構(gòu)造

假定Cs，α，為R1中一族概率密度函數(shù)，其s階導(dǎo)數(shù)存在，且| |

f（x）≤α α，s＞4為正整數(shù)。令 Kr（x）（r=0，1，…，s-1）是 Borel可測的有界函數(shù)，在區(qū)間（0，1）之外為0，且滿足條件（B）

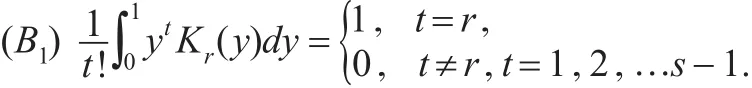
（B2）Kr（x）在R1上除有限點(diǎn)集E0外是可微的，

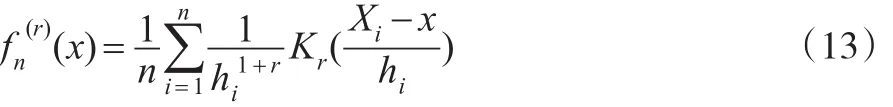
其中 hn↓0，Kr（x）是滿足條件 （B）的核函數(shù)，經(jīng)計(jì)算得：

由上式可知此估計(jì)具有一種遞歸性質(zhì)，用遞歸核估計(jì)去估計(jì) f（r）（x）時，由于可以進(jìn)行遞歸計(jì)算，在樣本點(diǎn)的增加情形下不需要重新計(jì)算所有項(xiàng)，僅計(jì)算新的添加項(xiàng)，如果用普通的核估計(jì)就必須重新計(jì)算所有項(xiàng)，因此采用遞歸核估計(jì)可以減少計(jì)算量。其次，遞歸核估計(jì)對不同區(qū)間可以選擇不同的適當(dāng)窗寬，從而可以克服估計(jì)的過度平滑和過度銳化，這樣能夠較為全面地刻畫密度函數(shù)，從而提高了估計(jì)的效率。

由式（10）和式（13）定義α（x）的估計(jì)量：

故EB檢驗(yàn)函數(shù)定義為:

令 En表示對的聯(lián)合分布求均值,則δn（x）的全面Bayes風(fēng)險(xiǎn)為：

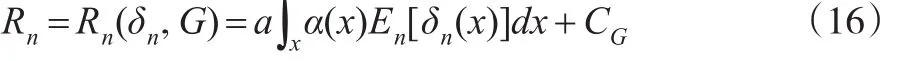
本文假定 c，c0，c1，c2… 為不依賴n的正常數(shù)。

（2）當(dāng)取時,對 0＜λ≤1,則有：

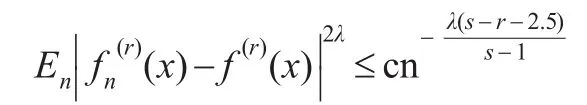
證明：（1）由Cr不等式可知,對r=0,1,2有：

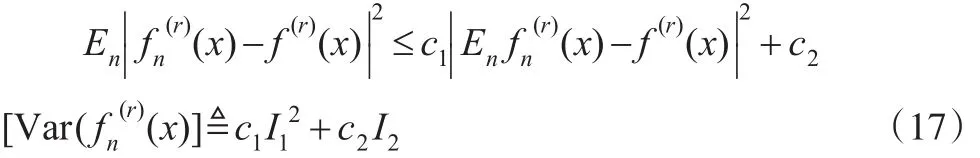
由式（13）和核函數(shù)的性質(zhì)可知：

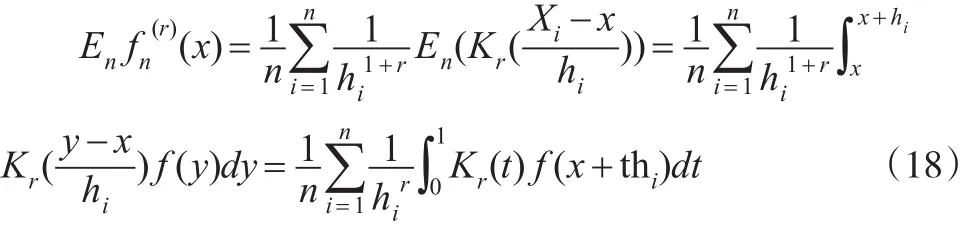
由Taylor展開得：

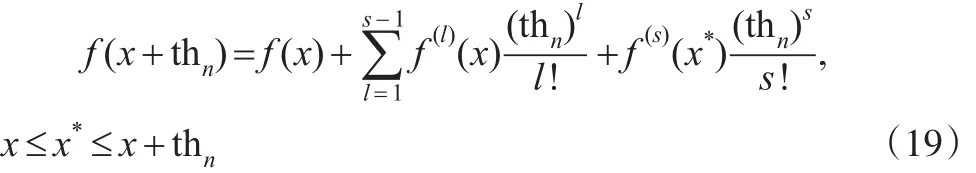
將式（19）代入式（18）可得：

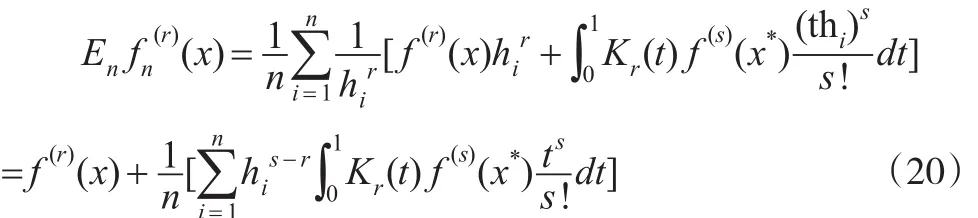
由 f（x）∈Cs，α，及| Kr（t）|≤C ，可知：

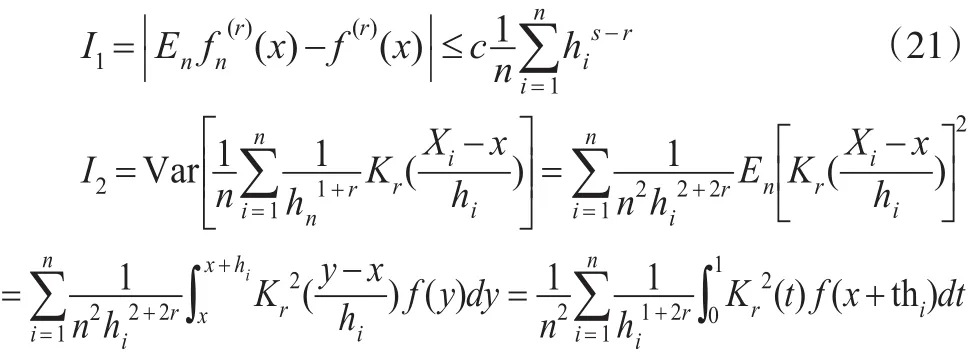
再由 f（x）∈ Cs，α，及| Kr（t）|≤M,hn單調(diào)遞減=0可知：

將 式（23）和式（24）代入式（17），結(jié)論（1）成立。

（2）由Cr不等式可知：

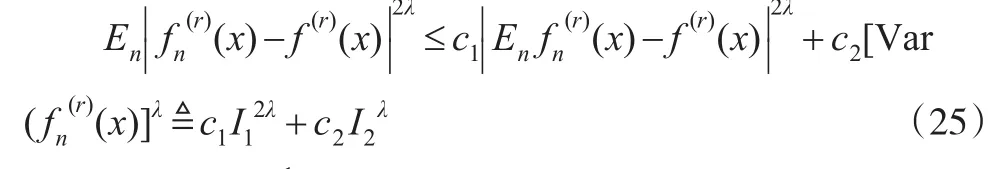
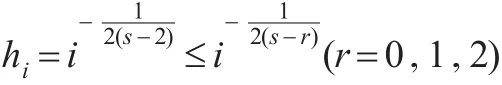
由式（21）可得：

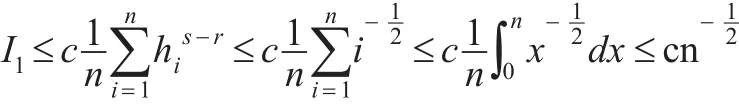
故有：

將式（26）和式（27）代入式（25），結(jié)論（2）成立。

引理2：令 R（G）和 Rn分別由式（12）和式（16）給出，則：

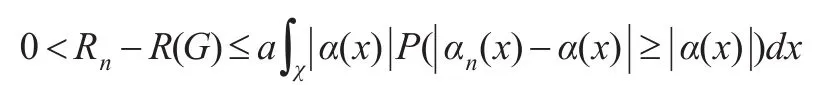
證明：見文獻(xiàn)[1]引理1。

2 EB檢驗(yàn)函數(shù)的主要結(jié)果

定理 1：設(shè) δn（x）由式（15）給出，其中為 iid樣本序列，假定條件（A）和（B）成立，若：

（3）f（r）（x）為x 的連續(xù)函數(shù)，則有

證明：由引理2可知：

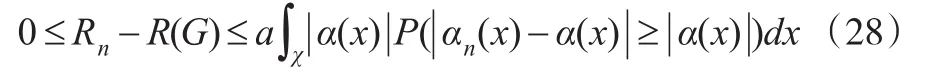
由式（8）和Fubini定理得：

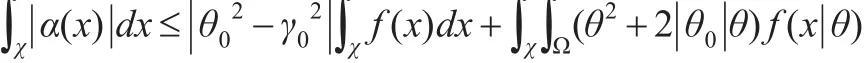
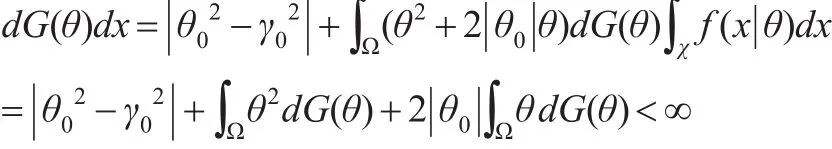
由控制收斂定理，可知：

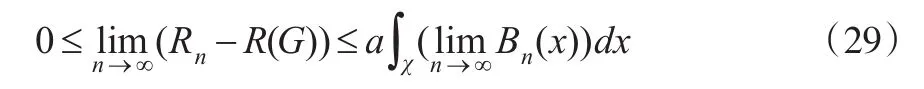
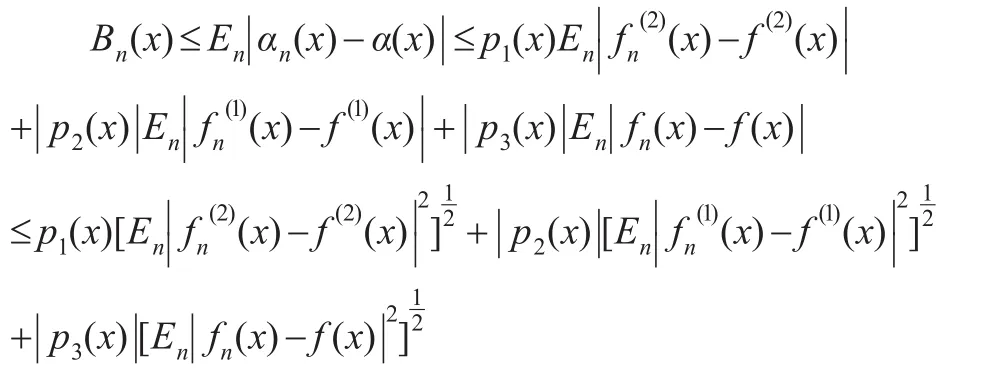
再由引理1（1）可知，對 x∈χ，當(dāng) r=0，1，2時有：

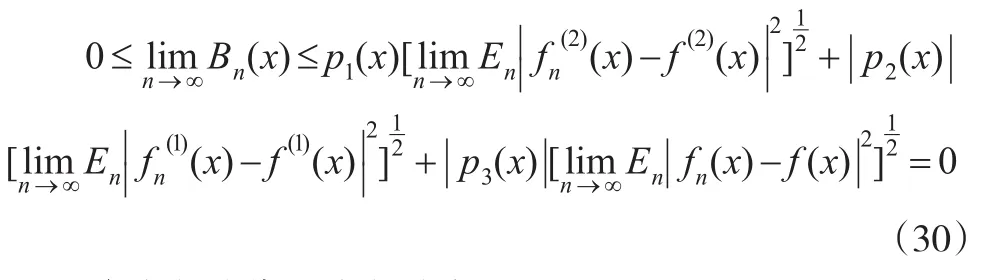
將式（30）代入式（29）定理得證。

定理2：設(shè) δn（x）由式（15）定義,其中 X1，X2，…，Xn為iid樣本序列,且假定（A和（B）成立,若0＜λ＜1,有：

證明：由引理2和Markov不等式，可知：

由引理1（2）可知：

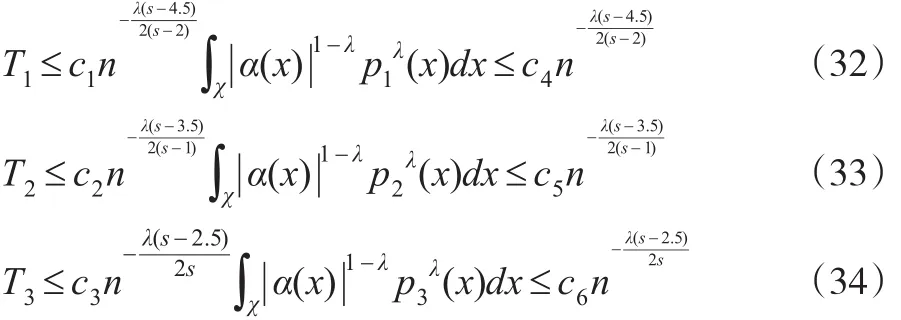
將式（32）至式（34）代入式（31）定理得證。

3 例子

下面舉例驗(yàn)證適合文中定理1與定理2條件的分布族和先驗(yàn)分布是存在的，在模型式（1）中，令 c（θ）=θ，u（x）=0，w（x）=-1，則隨機(jī)變量X分布為取 θ 的先驗(yàn)分布為Gamma分布族：

β和r為已知常數(shù)β＞0，r＞0.所以有：

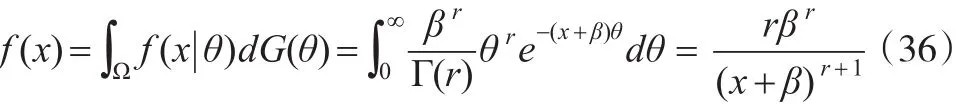
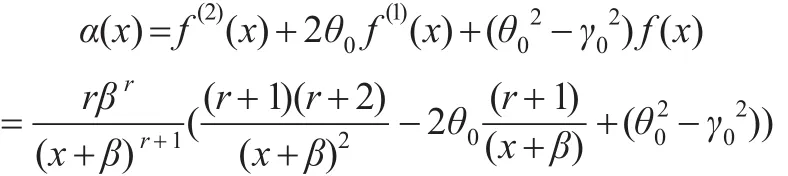
因此：

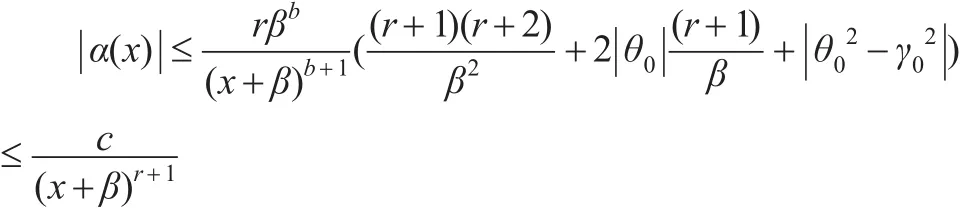
（1）由式（36）易見 f（x）為 x任意階可導(dǎo)連續(xù)且一致有界，即 f（x）∈Cs，α。

由于 β＞0，r＞0，這一積分為第1類廣義積分，當(dāng) （r+1）（1-λ）＞1時，即上述積分收斂。

由（1）—（3）可知，定理1和定理2條件均成立。

4 結(jié)論

本文在“平方損失”下，研究了一類廣義單參數(shù)指數(shù)分布族參數(shù)的經(jīng)驗(yàn)Bayes（EB）雙側(cè)檢驗(yàn)問題，利用概率密度函數(shù)的遞歸核估計(jì)，構(gòu)造了參數(shù)的EB檢驗(yàn)函數(shù)，本文采用“平方損失”和遞歸核估計(jì)，研究了相應(yīng)參數(shù)的雙側(cè)檢驗(yàn)，這與以往研究單參數(shù)指數(shù)分布族參數(shù)的EB檢驗(yàn)的文獻(xiàn)不同，本文在適當(dāng)?shù)臈l件下，證明了所提出的EB檢驗(yàn)函數(shù)的漸近最優(yōu)（a.o.）性，獲得了其收斂速度的階可任意接近于推廣現(xiàn)有文獻(xiàn)的相應(yīng)結(jié)果，并給出滿足條件結(jié)果的一個例子。

[1]Johns M V Jr,Van Ryzin J.Convergence Rates in Empirical Bayes Two-action ProblemsⅡ:Continuous Case[J].Ann.Math.Statist,,1972,（42）.

[2]Van Houwelingen J C.Monotone empirical Bayes Test for the Continu?ous One-Parameter Exponential Family[J].Ann.Statist.,1976,（4）.

[3]Liang Tachen.On empirical Bayes Tests in a Positive Exponential Family[J].Journal of Statistical Planning and Inference,2000,（83）.

[4]Liang Tachen.On Optimal Convergence Rate of Empirical Bayes Tests[J].Statistics&Probability Letters,2004，（68）.

[5]韋來生.刻度指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes檢驗(yàn)問題NA樣本情形[J].應(yīng)用數(shù)學(xué)學(xué)報(bào),2000,（23）.

[6]周雁,韋來生.刻度指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes檢驗(yàn)函數(shù)收斂速度的改進(jìn)[J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào),2008,23（2）.

[7]陳家清,劉次華.線性指數(shù)分布族參數(shù)的經(jīng)驗(yàn)Bayes檢驗(yàn)問題[J].系統(tǒng)科學(xué)與數(shù)學(xué),2008,28（5）.

[8]彭家龍,袁瑩.一類連續(xù)型單參數(shù)指數(shù)族參數(shù)的經(jīng)驗(yàn)Bayes檢驗(yàn)問題[J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào),2012,27（4）.

[9]樊家琨.概率密度函數(shù)及其導(dǎo)數(shù)遞歸核估計(jì)的強(qiáng)相合性[J].河南大學(xué)學(xué)報(bào)：自然科學(xué)版,1992,22（2）.