核電廠應急補水箱 (ASG)地震響應對比分析

韓 治,唐 暉,張春明,文 靜

(環境保護部核與輻射安全中心,北京 100082)

核電廠中存在大量的核安全級薄壁儲液容器,如輔助給水系統ASG水箱和換料系統PTR水箱等,其需要在地震情況下保持結構完整性及其功能。GB50267-97《核電廠抗震設計規范》要求 “對于薄壁儲液容器計算應計入器壁柔度的影響,并對壓應力進行儲液容器壁的失穩校核”[1]。

大型儲液容器在商業、軍用、民用、核電廠,尤其是在石油化工業中十分常見,多年來各領域的科研人員針對儲液容器的地震響應問題建立了行之有效的分析方法,詳細發展歷程請參考綜述性文獻[2]。1957年,Housner將剛性儲液容器化為質量彈簧系統的簡化模型[3],模型簡單實用,為六、七十年代儲液容器抗震計算所廣泛采用。然而,容器壁的剛性假設,導致求出的脈動液壓過小,按Housner理論設計的儲液容器在地震中仍大量損壞,從而使科研人員進一步開展柔性壁錨固式儲液容器的抗震研究。ASCE 4-98適用于核設施所有核安全相關結構,包括且不限于地面及地下結構、埋置管道、地面立式容器以及帶隔震系統的結構[4],核電廠大型儲液容器屬于該適用范圍內。ASCE 4-98標準的3.5節中給出了立式儲液容器的集中質量彈簧模型與抗震計算方法,考慮了柔性壁影響,以樓層反應譜為依據確定地震動輸入。基于集中質量-彈簧模型,多位研究人員在核電廠儲液容器的地震響應分析方面取得進展[5-8]。

近年來,隨著計算機硬件性能的提升和流固耦合計算方法的發展,利用流固耦合數值模擬方法,如任意拉格朗日歐拉方法 (ALE)、位移流體單元法、勢流體單元法、SPH粒子法和移動粒子法 (MPS)等,進行儲液容器地震響應分析研究工作越來越多[9-14]。其中,陸道綱等[15]采用ALE方法、衛媛媛等[12,16]采用勢流體單元法[12]、MPS方法[16]研究了快中子反應堆主容器的自由液面晃動問題。

本文利用ASCE4-98建議的集中質量-彈簧模型方法 (以下簡稱MASS-SPRING方法)和ANSYS流固耦合方法 (以下簡稱FSI方法)進行核電廠儲液容器地震響應分析,全面比較了兩者之間的差異,并分析了出現差異的原因。

1 儲液容器地震響應分析方法

1.1 集中質量-彈簧模型方法

ASCE4-98基于Housner理論給出了立式儲液容器的抗震計算模型,即集中質量-彈簧模型,見圖1。本文不對Housner計算模型做詳細介紹,僅列出與本文有關的一些假設[4]:流體無粘、無旋、不可壓;容器具有剛性的豎直側壁和水平底板 (由剛性容器導出的流體模型連接到彈性容器中,才能實現流體與彈性容器的耦合振動)。本文涉及的質量-彈簧模型及相關參數的計算公式見下文,主要取自文獻[17]。

等效脈沖質量公式如下

其中,MF是液體總質量,R是容器半徑,h是液位高度。

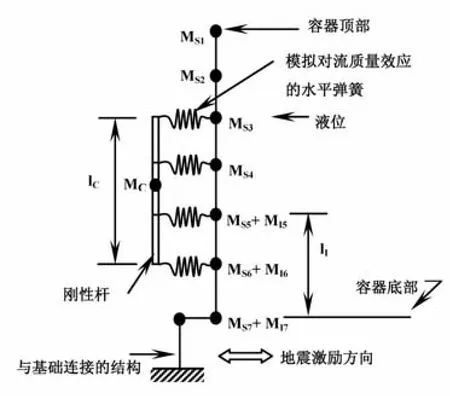
圖1 柔性壁儲液容器水平地震響應分析的流體質量分布Fig.1 Distribution of fluid mass for horizontal seismic response analysis of storage tank with flexible walls

圖1中,MS表示儲液容器質量;MI表示脈沖質量;MC表示對流質量;lI表示脈沖質量施加的區域;lC表示對流質量施加的區域。

脈沖質量的質心高度為

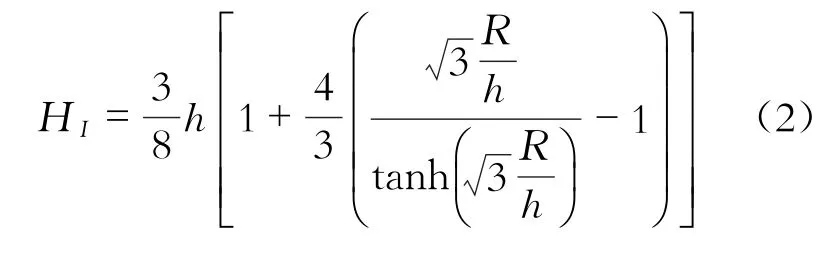
對流質量公式為

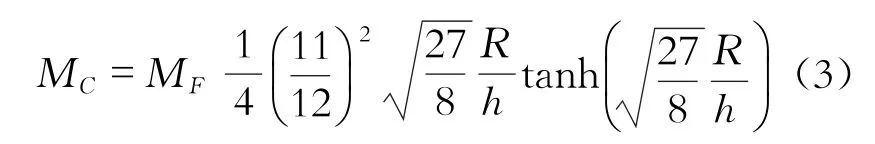
對流質量的質心高度HC為

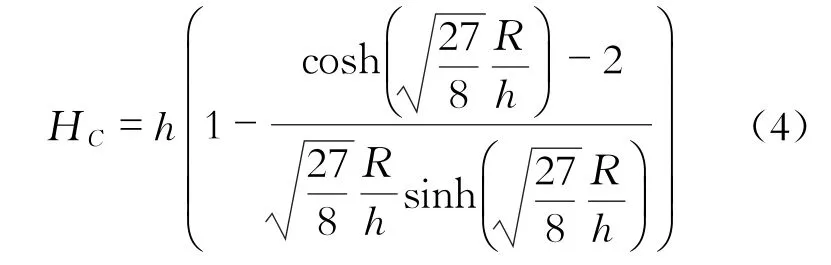
流體晃動對應的角頻率滿足:

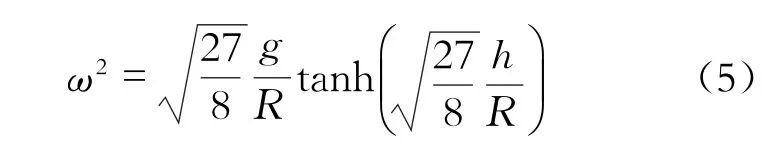
1.2 ANSYS流固耦合有限元方法

對于地震中的儲液容器,工程上主要關注儲液容器的形變和應力分布,通常可以假設流體為無粘、理想可壓縮和小擾動的,固體為線彈性的。采用流固耦合方法分析動力學問題時,對固體結構采用位移為基本變量,依據定義的流體和固體之間耦合作用傳遞方式的不同,流體可以采用位移、壓力以及各種勢函數作為基本變量,相應的流固耦合有限元格式可以是位移-壓力格式、位移-位移格式和位移-勢函數格式。ANSYS的流體單元FLUID80對應的是位移-位移格式,相應的有限元方程為

其中,Ms是固體的質量矩陣;Mf是流體的質量矩陣;Ks是固體的剛度矩陣;Kf是流體的剛度矩陣;Us是固體節點位移向量;Uf是流體節點位移向量。

2 算例:核電廠ASG水箱地震響應分析

2.1 ASG水箱結構

應急補水箱 (ASG)是核電廠余熱排出系統中的重要設備,在事故情況下確保向蒸汽發生器供應足夠的水,以排出堆芯的衰變熱,正確地評價ASG水箱在地震中的響應對核安全至關重要。

ASG水箱為立式儲液容器[5],由封頭、筒體、封底、筒體加強環等組成,結構如圖2所示。筒體由五層不同厚度的筒體段焊接而成,厚度分別為16mm、12mm、10mm、8mm、8mm,高度分別為3000mm、3000mm、3000mm、3000mm和2600mm,筒體外直徑為9700mm,加強環外半徑為5350mm,內半徑4850mm,厚度為10mm,液位標高為14520mm。容器主要材料為20HR-B,密度7850kg·m-3,泊松比0.3,材料力學性能見表1。

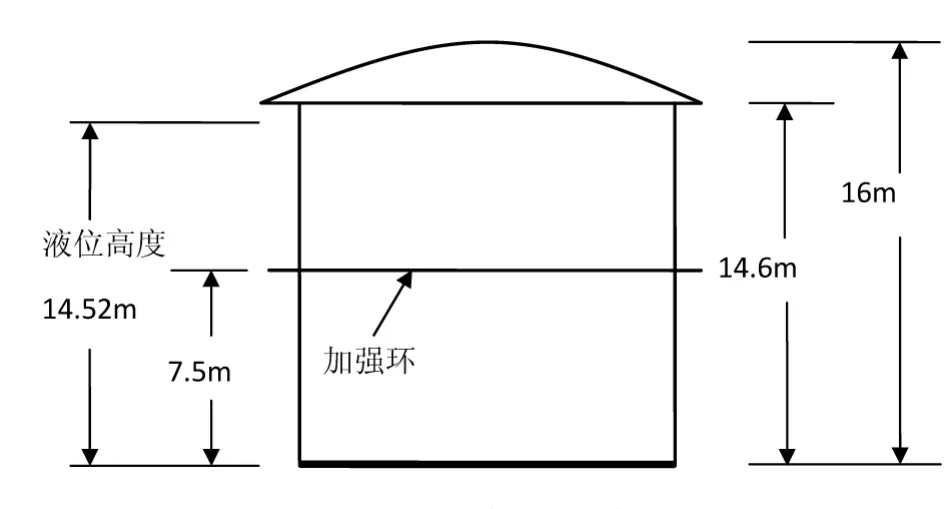
圖2 ASG水箱結構示意圖Fig.2 Schematic diagram of ASG tank

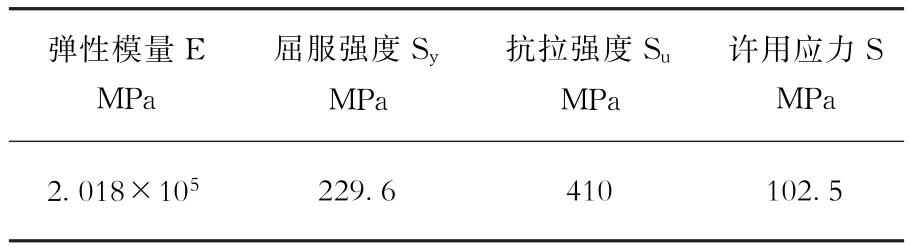
表1 材料的力學性能參數Table 1 Mechanical properties of the material

2.2 地震動輸入條件

本文的目的是研究 (滿水狀態)儲液容器地震響應分析方法,SSE地震的結構阻尼比取4%,地震作用下流體阻尼比取0.5%,為便于計算結果之間的比較,將地震動輸入條件簡化為如表2所示。

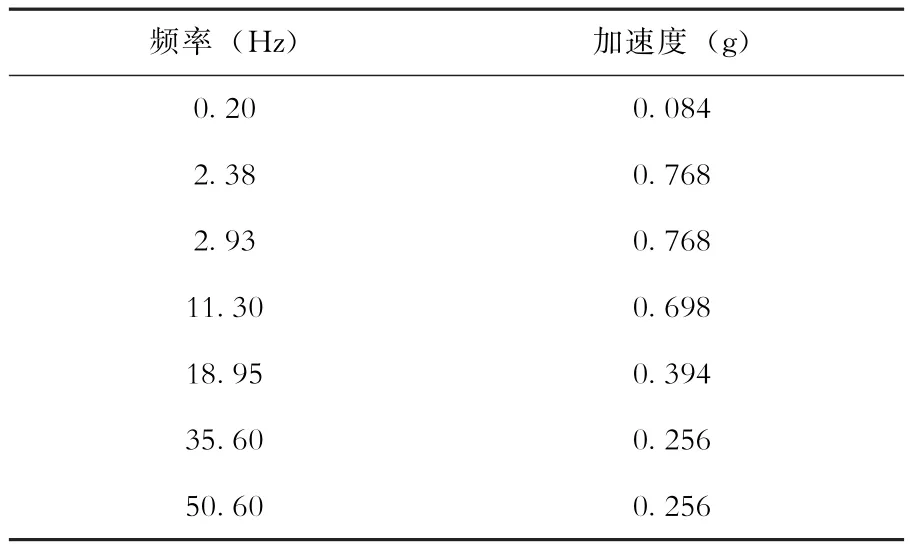
表2 SSE地震水平方向反應譜Table 2 seismic response spectrum of horizontal direction

2.3 模態分析

2.3.1 水箱模態分析 (MASS-SPRING方法)基于MASS-SPRING方法建立水箱有限元模型,如圖3所示,水箱采用殼單元SHELL281,質量點采用質點單元MASS21,彈簧采用彈簧單元COMBIN14。對水箱進行模態分析,前兩階為對流質量晃動頻率,均為0.3048 Hz;水箱整體一階梁式振型的頻率為6.865 Hz。

圖3 集中質量-彈簧有限元模型Fig.3 Finite element model based on Mass-Spring Method

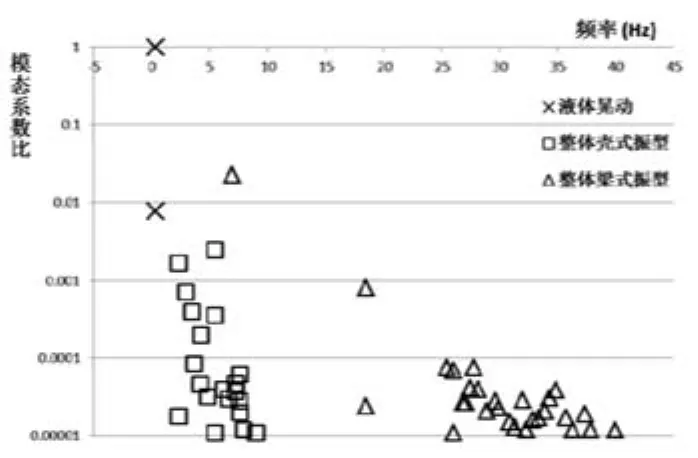
圖4 振型模態參與系數比分布 (MASS-SPRING方法)Fig.4 Modal participation coefficient ratio based on MASS-SPRING Method

模態分析得到的振型中就只有前兩階為代表流體晃動的振型,其他的都是水箱的振型。圖4給出了MASS-SPRING方法得到的振型模態參與系數比分布情況,模態參與系數比(M.C.RATIO)高于0.00001的振型有50個,其中代表液體晃動的振型2個,整體殼式振型20個,整體梁式振型28個。

2.3.2 水箱模態分析 (FSI方法)

基于ANSYS FSI方法建立水箱有限元模型,如圖5所示,水箱采用殼單元SHELL181,流體采用流體單元FLUID80。流體晃動一階振型2個,頻率均為0.3103 Hz,水箱整體一階梁式振型2個,頻率均為9.195 Hz。

模態參與系數比高于0.00001的流體振型413個,梁式振型7個,殼式振型5個,從圖6所示的振型模態參與系數比 (M.C.RATIO)分布圖,流體晃動振型和容器整體梁式振型占據主導地位。

圖5 ANSYSFSI有限元模型Fig.5 Finite element model based on FSI Method

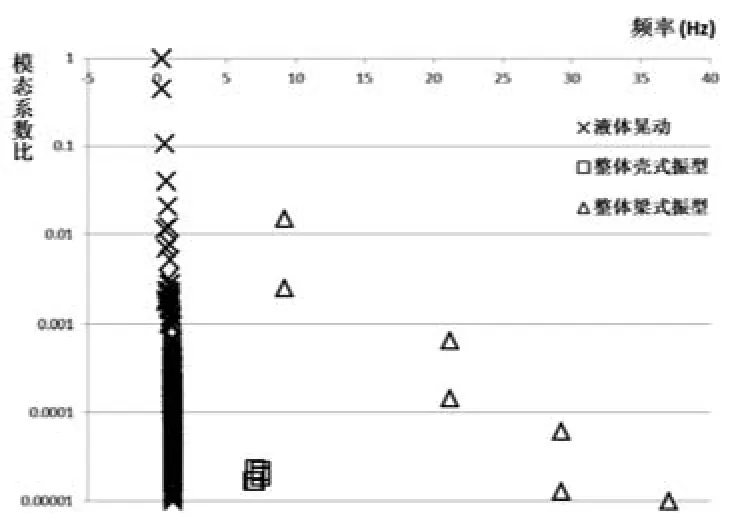
圖6 FSI方法得到的水箱振型模態系數比分布Fig.6 Modal participation coefficient ratio based on FSI Method

2.3.3 模態分析結果的對比

MASS-SPRING方法得到的流體一階振型的頻率為0.3048Hz,ANSYS FSI方法得到的流體一階振型的頻率為0.3103Hz,由公式(5)得到的流體一階振型的頻率為0.3068Hz,基本是一致的。

但是,比較圖4和圖6可以發現,MASSSPRING方法得到的振型中代表流體晃動的振型只有兩階,殼式振型占據了重要的地位;ANSYS FSI方法模態分析得到的振型中,流體振型和容器梁式振型占據主導地位。MASSSPRING方法得到的一階梁式振型的頻率為6.865Hz,ANSYS FSI方法得到的一階梁式振型的頻率為9.195Hz。兩種方法得到的一階梁式振型區別很大,這主要是因為兩種方法對于地震中流體固體之間的相互作用采用的建模方法差異很大,研究發現MASS-SPRING方法將流體對固體的脈沖作用簡化為脈沖質量,施加在水箱的下半部,脈沖質量和水箱在地震中完全同步,也就是等價于水箱下半部的水體在地震中和水箱完全同步,然而真實地震中水體達不到和水箱完全的同步運動,因此MASSSPRING方法的脈沖質量的假設方法,引入了明顯的保守性。

2.4 地震響應分析

2.4.1 水箱地震響應分析 (MASS-SPRING方法)

由于儲液容器在地震中主要的破壞形式是容器側壁底部區域附近的屈曲變形,所以實際工程問題關注水箱底部區域側壁的主應力S1和垂直軸向應力Sy。

圖7 水箱側壁面第一主應力S1Fig.7 First principal stress of side wall of tank

考慮靜水壓力、自重和水平X方向地震載荷,質量-彈簧模型方法得到如圖7、圖8所示應力結果,最大主應力S1出現在底部,為56.8MPa,最大的垂直軸向應力Sy同樣出現在底部,為56.8 MPa。比較主應力S1和軸向應力Sy的分布,可以看出在水平X方向地震載荷激勵下,水箱側壁面上Sy占據主導,符合地震中屈曲失穩破壞的容器的應力分布特點。

圖8 水箱側壁面的垂直軸向應力SyFig.8 Vertical axial stress of side wall of tank

2.4.2 水箱地震響應分析 (FSI方法)

基于ANSYS FSI方法的水箱地震響應分析,首先進行水箱靜力學分析,再進行預應力模態分析和譜分析。從圖9、圖10應力分布圖可以看出,最大主應力S1出現在水箱底部,達到22.3 MPa,最大軸向應力Sy出現在水箱底部,達到22.1 MPa,對比S1和Sy可以看出,水箱底部的應力Sy占據主導地位。圖11、圖12給出重力作用下水箱的應力結果,最大周向應力為26.2MPa,最大軸向應力為7.88MPa,靜力學分析得到的應力分布是預應力模態分析的初始輸入數據。水箱在地震激勵下真實的應力分布需要由譜分析應力結果迭加靜力學分析應力結果來得到。

圖9 水箱側壁面的第一主應力S1Fig.9 First principal stress of side wall of tank

圖10 水箱側壁面的軸向應力SyFig.10 Vertical axial stress of side wall of tank

圖11 重力載荷作用下水箱的周向應力Fig.11 Circumferential stress of tank under gravity loading

圖12 重力載荷作用下水箱的軸向應力Fig.12 Axial Stress of Water Tank under Gravity Load

2.4.3 地震響應分析結果的對比

大型薄壁儲液容器在地震中的主要破壞形式是屈曲失穩,軸向應力Sy是屈曲與否的關鍵。從圖8、圖10、圖12中選取底部附近水箱側壁面的垂直軸向應力Sy,形成圖13所示的軸向應力Sy對比結果。可以看出兩種方法得到的軸向應力Sy趨勢相同,底部軸向應力Sy最大,隨垂直坐標Y的升高,水箱側壁面軸向應力Sy不斷下降,在水箱壁厚變化的結構不連續處Sy出現波動現象。

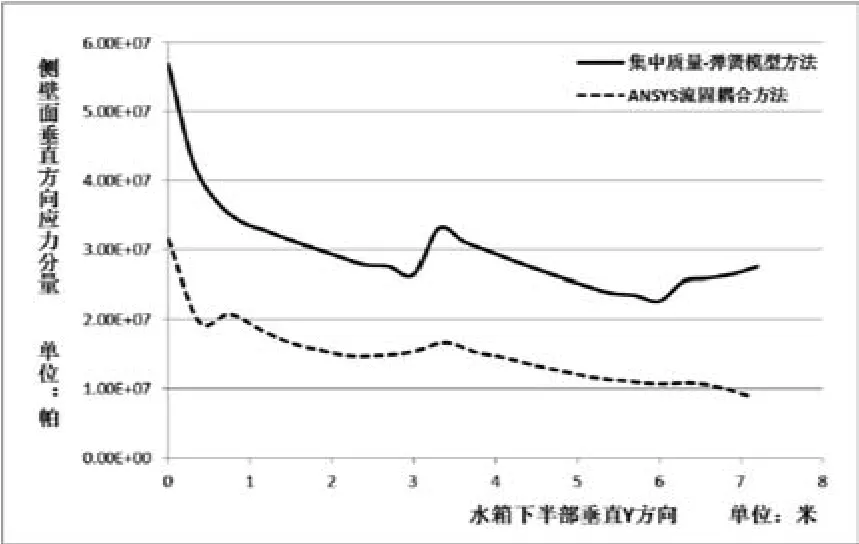
圖13 水箱下部壁面垂直方向應力Sy計算結果對比圖Fig.13 Comparison of the vertical stress in bottom of tank

但是,兩種方法得到的軸向應力存在明顯的差異,MASS-SPRING方法得到的應力Sy比ANSYS FSI方法得到的應力Sy高80%左右。

究其原因,由表3所示的振型有效質量、振型有效質量與總有效質量之比這兩個參數可以計算出,MASS-SPRING方法建立的有限元模型的總有效質量為1319937kg,而ANSYS FSI方法建立的有限元模型的總有效質量為1172651kg(約等于水箱的真實總質量)。這說明,MASS-SPRING方法在建模過程中確定的對流質量和脈沖質量偏保守,計算中發現,脈沖質量對模態分析得到的梁式振型的頻率和地震響應分析得到的應力結果起著決定性的影響,計算結果對對流質量不敏感。MASS-SPRING方法將脈沖質量施加在水箱的下半部,脈沖質量和水箱在地震中完全同步,使得地震響應分析得到的軸向應力Sy結果偏保守。

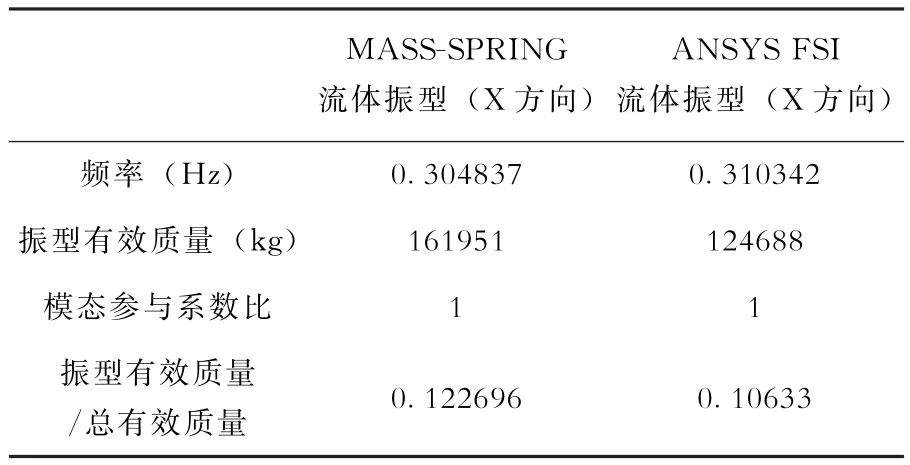
表3 重要模態有效質量和模態參與系數比Table 3 Effective mass and modal participation coefficient ratio of significant mode

3 結 論

本文分別利用MASS-SPRING方法和ANSYS FSI方法對核電廠ASG水箱進行地震響應分析,兩種方法得到的地震響應分析結果差異明顯。

兩種方法得到的模態分析和地震響應分析結果出現差異的原因如下:

(1)MASS-SPRING方法把流體對水箱的作用等效為集中質量-彈簧系統,施加在水箱上部,脈沖質量均布在水箱下半部,從而將流固耦合問題轉化為傳統的結構動力學問題。模態分析結果表明,MASS-SPRING方法建立的有限元模型的總有效質量為1319937 kg,而ANSYS FSI方法建立的有限元模型的總有效質量為1172651 kg(約等于水箱的真實總質量),MASS-SPRING方法建模過程中的保守假設,使得有限元模型的有效質量明顯超出真實總質量。

(2)MASS-SPRING方法將流體對固體的脈沖作用簡化為脈沖質量,施加在水箱的下半部,脈沖質量和水箱在地震中完全同步,也就是等價于水箱下半部的水體在地震中和水箱完全同步,然而真實地震中水體達不到和水箱完全的同步運動,因此MASSSPRING方法的脈沖質量的假設方法,引入了明顯的保守性,相應的,地震響應分析得到的應力結果偏保守。

綜上所述,基于兩種方法進行核電廠儲液容器的地震響應分析,ANSYS FSI方法得到的應力結果明顯小于MASS-SPRING方法得到的應力結果,MASS-SPRING方法得到的應力結果是偏保守的。對于ANSYS FSI方法得到的應力結果將進一步進行試驗驗證。

[1]國家地震局.GB50267-97核電廠抗震設計規范[S].北京:中華人民共和國建設部,1997.

[2]溫德超,鄭兆昌,孫煥純.儲液罐抗震研究的進展[J].力學進展,1995,25(1):60-76.

[3]HOUSNER G W.Dynamic pressures on accelerated fluid containers[J].Bulletin of the Seismological Society of America.1957,47(1):15-35.

[4]ASCE.ASCE 4-98 Seismic Analysis of Safe-related Nuclear Structures and Commentary[S].Reston:ASCE,1999.

[5]文靜,路燕,徐宇,等.核電廠輔助給水系統水箱抗震分析研究[J].原子能科學技術,2015,49(5):897-902.

[6]李楠,韓治.采用組合質量-彈簧模型的快堆臥式貯鈉罐晃動分析[J].原子能科學技術,2015,49(9):1642-1647.

[7]WEN Jing,LU Daogang,GAO Xiaoan,et al.Mass-spring model used to simulate the sloshing of fluid in the container under the earthquake[C].18th International Conference on Structural Mechanics in Reactor Technology(SMiRT-18).Beijing:Atomic Energy Press,2005:3636-3644.

[8]劉嘉一,白欣然,李曉軒.質量-彈簧模型在儲液容器抗震分析中的應用[J].原子能科學技術,2013,47(6):947-951

[9]李彥民,徐剛,任文敏,等.儲液容器流固耦合動力響應分析計算[J].工程力學,2002(4):29-32.

[10]徐剛,任文敏,張維,等.儲液容器的三維流固耦合動力特性分析[J].力學學報,2004(3):328-335.

[11]陸道綱,張立殷.核電廠中流固耦合現象數值模擬研究綜述[J].原子能科學技術,2009,43(S1):76-83.

[12]衛媛媛,陸道綱,梁亞平.與流體晃動相耦合的快堆主容器地震響應的數值模擬[J].原子能科學技術,2008,42(S2):472-476.

[13]王建軍,李其漢,朱梓根,等.自由液面大晃動的流固耦合數值分析方法研究進展[J].力學季刊,2001(4):447-454.

[14]GOUDARZI M A.Seismic Behavior of a Single Deck Floating Roof Due to Second Sloshing Mode[J].Journal of Pressure Vessel Technology,2012,135(1):244-252.

[15]陸道綱.CEFR主容器內正弦三波激勵下液面晃動響應[J].核科學與工程,2003,23(4):306-310.

[16]衛媛媛,陸道綱.基于移動粒子法的快堆自由表面流體對容器頂蓋沖擊現象的數值模擬.原子能科學技術,2009,43(10):910-914.

[17]居榮初,曾心傳.彈性結構與液體的耦聯振動理論[M].北京:地震出版社,1983:115-123.