高緯度BDS/GPS PPP中的對流層延遲改正模型優選

周潤楊,薛玫嬌

(1.92941部隊，遼寧 葫蘆島 125000；2.西安科技大學，陜西 西安 710054)

高緯度BDS/GPS PPP中的對流層延遲改正模型優選

周潤楊1,薛玫嬌2

(1.92941部隊，遼寧 葫蘆島 125000；2.西安科技大學，陜西 西安 710054)

由于高緯度地區氣溫氣壓值及變化率與中低緯度地區有較大差異，因此目前發布的多種對流層延遲模型在高緯度地區使用的精度會不同。為了給高緯度地區BDS/GPS用戶提供更好的對流層延遲模型選擇，文中采用UNB3，EGNOS和GPT2模型，以IGS發布的ZPD產品和SINEX文件作為參考，對比基于這三種對流層延遲模型計算的天頂對流層總延遲量以及精密單點定位精度，可知GPT2較UNB3和EGNOS在高緯度地區定位中有更好的精度表現。

BDS/GPS；高緯度；對流層延遲模型；定位精度；天頂對流層延遲

到目前為止，由于缺乏足夠的可視衛星，北斗衛星導航系統(BDS)單系統不能為高緯度(緯度超過60°)地區全部提供可用和可靠的導航定位服務[1-4]，但是通過BDS和全球定位系統(GPS)的組合(BDS/GPS)，可以獲得更多的可視衛星，且衛星幾何構型也更好[1-2,4]，其中，在高緯度地區，基于BDS/GPS的位置精度因子(PDOP)值在1.0～3.1變動，這一值要比基于單BDS和單GPS的PDOP值要小[1]。另外，對于高緯度地區的BDS/GPS用戶來說，由于缺少地基增強系統參考站，精密單點定位(PPP)技術是目前能提供厘米級精度定位最好的選擇。因此，本文選擇基于BDS/GPS PPP定位模式進行研究。

在BDS/GPS PPP定位模式下，對流層延遲是影響定位結果的主要誤差源，其中包括靜力學延遲(干分量)和非靜力學延遲(濕分量)。過去，用經驗模型來改正對流層延遲，例如被廣泛使用的Hopfield模型和Saastamoinen模型，對流層延遲的值隨著衛星至接收機的高度角變化，高度角越低，延遲越大，最小約2.5 m,最大約20m[5]。

隨著地基GNSS觀測網的發展與完善，更多更廣泛的GNSS觀測量被獲取，這些全球分布的觀測量被用于創建更加高精度高分辨率的對流層延遲改正模型，例如UNB模型、EGNOS模型等等[6-8]，這些模型計算出的對流層總延遲量和天頂延遲量相對于簡單的、低精度的模型來說，計算過程比較復雜，但精度更高。在通常環境下，使用UNB3模型計算的天頂對流層延遲總量(ZTD)的平均偏差(bias)為2.0 cm，標準偏差(STD)為4.8 cm,均方根誤差為5.2 cm[8]。

但是UNB模型和EGNOS模型等作為僅基于緯度和高程計算的對流層延遲改正模型，在ZTD真值和緯向平均值差別大的地區，計算結果可能會引起比較大的誤差[5,9]。因此，為解決這一問題，多位學者基于三維格網氣象數據構建新的對流層延遲模型，例如GPT2模型等[5,10-11]。

對于高緯度地區的BDS/GPS PPP，衛星高度角要比中低緯度普遍要低一點，這樣會導致更大的對流層延遲、更大的PDOP值和更少的可視衛星[1]。由于高緯度地區的地基GNSS觀測站比較少，對流層模型在高緯度地區的精度相對于模型的整體精度會稍差，而且高緯度地區的溫度、濕度和氣壓與中低緯度有著很大差別，所以對流層延遲模型在高緯度地區BDS/GPS PPP中的精度表現會有所不同。文獻[12]便指出，在南極地區，采用Saastamoinen模型和Hopfield模型結合實測探空氣象數據計算的對流層延遲量精度相比于UNB3和EGNOS模型計算的更高[13]。

但是實測氣象數據不便于獲取，僅有氣象設備的GNSS觀測站才有條件獲取，對于一般用戶來說，高精度的氣象模型才更加方便使用。因此，為了在高緯度地區BDS/GPS PPP中選擇一個比較合適的對流層延遲改正模型，本文綜合比較基于UNB3,EGNOS和GPT2這3個常用的高精度模型計算的對流層天頂延遲總量估計精度和BDS/GPS PPP解算結果的精度，得出GPT2相比于UNB3和EGNOS在高緯度地區BDS/GPS PPP中精度最好的結論。

1 對流層延遲改正模型

1.1 UNB3模型

UNB3模型是Collins和Langley[6]為廣域增強系統(WAAS)用戶使用設計的，它的算法是基于一個氣象參數查閱表，如表1所示，其中包括溫度T0、壓強P0、水汽壓e0、溫度梯度β0和水汽梯度λ0。

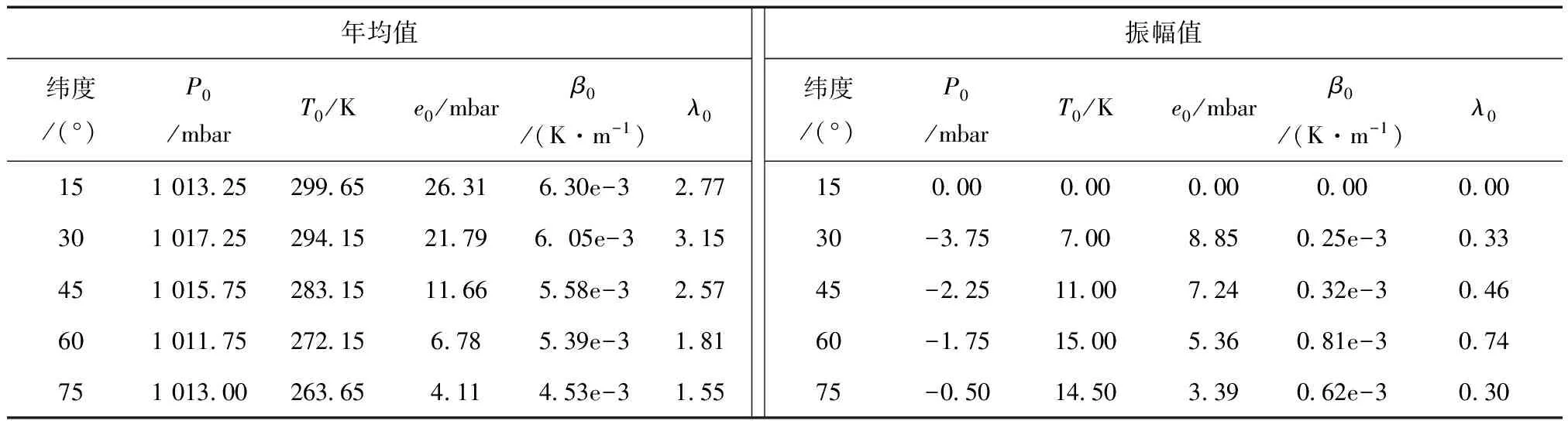
表1 5個氣象參數的年均值與振幅值查閱表

UNB3模型計算對流層總延遲量首先是獲取用戶對應的緯度和年積日，然后根據查閱表和算式(1)計算出氣象參數年均值和振幅值。

(1)

式中：φ代表用戶的緯度值；AVGφ是待計算的氣象參數年均值；LATi表示與用戶緯度相鄰的查閱表中較小的緯度值，另外，振幅值AMPφ的計算采用的是與年均值一樣的插值算法。然后再利用計算出的用戶緯度的年均值和振幅值，根據算式(2)得到5個氣象參數。

Xφ,doy=AVGφ+AMPφ×

(2)

(3)

(4)

λ′=λ+1.

(5)

gm=9.784[1-2.66×10-3cos(2φ)-

2.8×10-7H]，

(6)

(7)

對流層天頂延遲總量計算方法如式(8)，其中映射函數m采用Niell模型[11]。

(8)

1.2 EGNOS模型

Penna提出EGNOS模型算法[7]，該產品同樣基于氣象參數查閱表。年均值與振幅值的計算方法與UNB3模型相同，但是在計算用戶處平均海平面的5個氣象參數時，dmin的取值是根據用戶所處半球決定的，北緯取28,南緯取211。

EGNOS模型的天頂對流層干分量和濕分量由式(9)和式(10)計算。

(9)

(10)

k2=382 000 K2·mbar-1，

(11)

gm=9.784 m·s-2.

(12)

得到EGNOS模型的干、濕分量后，總路徑延遲可由式(13)計算，映射函數僅與衛星高度角α有關。

(13)

(14)

1.3 GPT2模型

GPT2氣象模型是Lagler等[10]基于10年(2000—2010年)的5°×5°全球月平均溫度和壓強格網數據創建的，這個格網數據來源于歐洲天氣預報中心(ECMWF)的數據庫ERA37。

GPT2模型格網數據可提供氣溫、氣壓等參數,用戶高程H處的溫度T和氣壓P則可由式(15)～式(17)計算得到。

P=Pr(1-0.000 022 6(H-Hr))5.225，

(15)

T=Tr+H×dT/dH，

(16)

dT/dH=-0.006 5 ℃/m.

(17)

式中：Pr是平均海平面壓強；Hr表示平均海平面高；Tr表示平均海平面溫度； dT/dH等于高程方向的溫度衰減率。

得到用戶處的溫度和壓強后，天頂對流層干、濕分量可由式(18)、式(19)計算得到。

(18)

(19)

GPT2模型在計算對流層路徑總延遲時一般采用的是GMF映射模型[13]，總延遲計算方法如式(20)。

(20)

2 實驗數據與解算策略

實驗數據選取了國際全球衛星導航系統服務機構(international GNSS service，IGS)提供的多衛星導航系統實驗(multi-GNSS experiment,MGEX)觀測網中的4個高緯度站點，即KIRU,METG,REYK和OHI3站點的2015年年積日為322～364 d(8 d數據丟失)的BDS/GPS雙系統雙頻的觀測數據，4個站點的位置如圖1所示，其中KIRU，METG和REYK站分布在北半球，OHI3站在南半球。

圖1 KIRU，METG，REYK和OHI3站點全球分布情況

本文BDS/GPS PPP解算采用無電離層組合觀測值。由于軌道產品和鐘差產品在精度上BDS衛星不如GPS衛星[14]，因此，本文將BDS和GPS觀測值的權重比設置為1∶4，為獲取更多的觀測值和可視衛星，高度角設置為5°。本文采用的BDS/GPS PPP解算策略如表2所示。

表2 BDS/GPS PPP解算策略表

3 實驗結果分析

由于IGS 提供的對流層延遲產品(zenith path delay，ZPD)精度為4 mm，IGS提供的天頂站點坐標精度為水平3 mm，高程6 mm[15]，因此，本文采取IGS提供的ZPD產品和IGS站周解文件作為天頂對流層延遲總量和坐標的參考真值。

如表3所示，基于GPT2模型計算出的ZTD值的RMS為0.79 cm，相比于UNB3模型和EGNOS模型分別低83.7%和80.2%。基于UNB3和EGNOS模型計算的ZTD值的STD都在1.3 cm的水平，基于GPT2模型該值降低到0.65 cm。KIRU,METG和REYK站點都坐落在北半球，在這3個站點，基于3個模型計算出ZTD值的平均偏差和RMS都呈現出一個共同規律，即GPT2模型的精度要比EGNOS模型高，EGNOS模型的精度比UNB3高。但是在坐落在南半球的OHI3站點，3個模型中，UNB3模型卻比EGNOS模型精度稍高，GPT2模型在精度上的表現依然最好。引起這一現象的原因可能是UNB3模型與EGNOS模型由于式中dmin的取值不同導致的。

表3 35 d時間內基于3種模型計算的ZTD值與ZPD產品比較差值的平均偏差，STD和RMS cm

如圖2所示，基于GPT2模型計算出的ZTD估計值更加接近于對應的IGS提供的ZPD產品值，基于UNB3和EGNOS模型計算的ZTD值偏離ZPD產品比較大，且存在一定的系統偏差，為了分析這個系統誤差的特性，本文將基于3個模型計算的ZTD值與ZPD值作差得到dZTD，形成如圖3的時間序列圖，對于GPT2模型，該差值在0 cm附近浮動，且其4個站差值的平均值為0.45 cm，最小0.13 cm，最大0.68 cm。然而，對于UNB3和EGONOS模型，該差值的絕對值均隨著時間推移而增加，且均大于1 cm，這一季節現象與文獻[9]中的年變化規律比較吻合。

上述結果顯示，在高緯度地區，相比于UNB3和EGNOS模型，GPT2模型可以提供更好的ZTD估計精度。另外EGNOS模型在北半球高緯度地區的ZTD估計精度表現上優于UNB3模型，在南半球情況則相反。

為了繼續判定3個模型在高緯度地區定位中的適用性表現，本文還比較基于這3個對流層延遲改正模型計算的BDS/GPS PPP結果的定位精度。

如圖4所示，在KIRU，METG，OHI3和REYK站點，基于3個模型計算的東、北方向定位誤差均小于3 cm，天頂方向誤差在6 cm以內，而且基于3種模型計算的東、北方向定位誤差在同一個站點幾乎相同，它們之間的相對誤差小于2 %。然而，在天頂方向基于這三種模型的定位精度有著顯著差異，其中，基于GPT2和UNB3模型計算的天頂方向誤差非常相近，且明顯小于基于EGNOS模型計算的天頂方向誤差，值得補充的是，基于EGNOS和UNB3模型計算的天頂方向誤差之間存在一個約4 cm的固定差值,產生這一巨大差值的原因可能與EGNOS模型采用的映射函數精度有關。通過比較基于GPT2和UNB3模型計算的天頂方向誤差的絕對值，發現在KIRU，METG，OHI3和REYK站點，基于UNB3模型的天頂方向誤差絕對值大于基于GPT2模型的比率分別為12.3%、4.5%、23.4%和16.2%。因此，GPT2模型對提高BDS/GPS PPP天頂方向誤差精度的貢獻要比UNB3大。

圖2 4個站點35 d中ZPD產品值與對應的基于模型計算的ZTD值時間序列圖

圖3 4個站點35 d中基于模型計算的ZTD值與對應的ZPD產品值的差值時間序列圖

圖4 4個站點35 d中基于3種對流層模型計算的BDS/GPS東北天方向誤差時間序列圖

如表4所示，基于3種對流層延遲改正模型計算的BDS/GPS PPP水平平均誤差值均為0.86 cm，說明選取不同的對流層延遲改正模型對BDS/GPS PPP整體的水平定位精度幾乎沒影響。在高程方向，基于GPT2-Saas模型計算的BDS/GPS PPP平均誤差為1.39 cm，比基于UNB3和EGNOS模型的分別小13.1%和47.4%。因此，從整體精度來看，GPT2-Saas模型在極地地區BDS/GPS PPP定位精度上表現最佳，UNB3模型也可為BDS/GPS PPP定位貢獻1 cm以內的水平精度和2 cm以內的高程精度。

表4 4個站點35 d里基于3種對流層模型計算的BDS/GPS水平、高程平均誤差表 cm

4 結束語

在高緯度站點KIRU，METG，OHI3和REYK，本文通過比較35 d中基于UNB3，EGNOS和GPT2模型的對流層延遲估計精度、定位精度，得出以下結論：

1)GPT2模型在ZTD值估計和高程定位精度上相比于UNB3和EGNOS模型表現最好。

2)EGNOS模型用于估計ZTD值的精度在北半球比UNB3高。但是在南半球， UNB3模型精度卻稍低于EGNOS模型，引起這一現象的原因可能是dmin取值不同導致的。

3)基于3種模型計算的BDS/GPS PPP水平誤差幾乎相同。在高程方向，基于GPT2模型計算的BDS/GPS PPP平均誤差比基于UNB3和EGNOS模型的分別小13.1 %和47.4 %。

4)EGNOS模型在BDS/GPS PPP高程精度上的表現明顯不如UNB3模型，其原因可能是EGNOS模型采用的映射函數精度不如UNB3模型。

[1] 楊元喜,徐君毅.北斗在極區導航定位性能分析[J].武漢大學學報(信息科學版),2016，41(1):15-20.

[2] 許 艷.南極GNSS精密定位若干問題研究[D].西安:長安大學,2012:28-31.

[3] 杜玉軍,王澤民,安家春,等. 北斗系統在遠洋及南極地區的定位性能分析[J].極地研究,2015,27(1):91-97.

[4] 尹子明,劉天恒,張樹為,等. BDS地基增強系統單雙模定位性能比較[J].導航定位學報,2016,4(3):64-68.

[5] LI W, YUAN Y B, OU J K, et al. A new global zenith tropospheric delay model IGGtrop for GNSS applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132-2139.

[6] COLLINS J P, LANGLEY R B. Estimating the residual tropospheric delay for airborne differential GPS positioning (A Summary)[M]//Advances in Positioning and Reference Frames. Springer Berlin Heidelberg, 1998: 331-336.

[7] PENNA N, DODSON A, CHEN W. Assessment of EGNOS tropospheric correction model[J]. The Journal of Navigation, 2001, 54(01): 37-55.

[8] LEANDRO R, SANTOS M C, LANGLEY R B. UNB neutral atmosphere models: development and performance[C]//Proceedings of ION NTM. 2006, 52(1): 564-73.

[9] ZHANG H, YUAN Y, LI W, et al. Assessment of Three Tropospheric Delay Models (IGGtrop, EGNOS and UNB3m) Based on Precise Point Positioning in the Chinese Region[J]. Sensors, 2016, 16(1): 122.

[10] LAGLER K, SCHINDELEGGER M, B?HM J, et al. GPT2: Empirical slant delay model for radio space geodetic techniques[J]. Geophysical research letters, 2013, 40(6): 1069-1073.

[11] NIELL A E. Global mapping functions for the atmosphere delay at radio wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246.

[12] 徐優偉, 張勝凱, 鄂棟臣, 等.4種對流層模型在南極地區的適用性分析[J].測繪地理信息, 2016, 41(4): 18-22.

[13] KOUBA J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses[J]. Journal of Geodesy, 2009, 83(3-4): 199-208.

[14] LI M, QU L, ZHAO Q, et al. Precise point positioning with the BeiDou navigation satellite system[J]. Sensors, 2014, 14(1): 927-943.

[15] DOW J M, NEILAN R E, RIZOS C. The international GNSS service in a changing landscape of global navigation satellite systems[J]. Journal of Geodesy, 2009, 83(3-4): 191-198.

Optimal selection of the troposphere delay models in high-latitude BDS/GPS PPP

ZHOU Runyang1，XUE Meijiao2

(1.Troops 92941, Huludao 125000,China；2. Xi’an University of Science and Technology, Xi’an 710054，China)

Because the variations of temperature and pressure at high-latitude are different from low- and mid-latitude regions, the released tropospheric delay models may perform diversely at high-latitude regions. In order to provide better selection of troposphere delay model for BDS/GPS PPP users, the performances of the University of New Brunswick 3 (UNB3) model, European Geostationary Navigation Overlay Service (EGNOS) model and Global Pressure and Temperature 2(GPT2) model are used in zenith tropospheric delay (ZTD) estimating and BDS/GPS PPP solutions are compared with the reference of ZPD products and SINEX files provided by IGS. The result shows that the GPT2 model performs better than UNB3 and EGNOS model in high-latitude positioning.

BDS/GPS; high-latitude; troposphere delay model; positioning precision; ZTD

2017-05-20

周潤楊(1991-)，男，碩士.

著錄：周潤楊,薛玫嬌.高緯度BDS/GPS PPP中的對流層延遲改正模型優選[J].測繪工程，2018，27(2)：20-25，31.

10.19349/j.cnki.issn1006-7949.2018.02.004

P228

A

1006-7949(2018)02-0020-06

張德福]