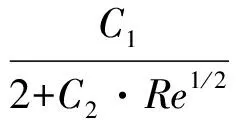球狀金屬顆粒在流動熔體中熔化過程的數學模型
牛 冉,李寶寬,劉中秋,李向龍
(東北大學 冶金學院,沈陽 110819)
球狀金屬顆粒在流動熔體中熔化過程的數學模型
牛 冉,李寶寬,劉中秋,李向龍
(東北大學 冶金學院,沈陽 110819)
針對冶金過程中常涉及到的固態金屬在液態金屬中的熔化過程建立數學模型,用焓法描述相變過程,采用有限體積法,對過熱熔體中球狀金屬顆粒熔化過程及其影響參數進行研究.結果表明,金屬顆粒的熔化受顆粒初始溫度、熔體過熱度以及熔體流動強度的影響.熔體流動對相變影響作用較大,受周圍流體對流強度的影響,顆粒從表面凝固殼形成到熔化過程呈現非均勻性,在靠近上游的顆粒前端以及下游尾跡處顆粒熔化速度較快,而顆粒邊緣熔化速度較慢.
熔化過程;數學模型;球狀金屬顆粒
相變過程直接影響材料加工、連續鑄造、包覆電鍍等過程的生產效率,其中一些過程涉及球狀金屬顆粒在其過熱液態形式中的熔化.事實上,對于凝固過程,由于冷卻環境容易得到,因此目前研究較多.而對于熔化過程,特別是金屬的熔化,需要維持高于金屬熔點的溫度,這需要消耗大量能源,所以對于熔化的研究相對較少.固體金屬顆粒熔化過程中熱傳遞特性對冶金過程的優化設計具有重要意義.
許多學者對不同材料的顆粒在其熔體中的熔化過程進行了研究.Hao等[1-2]通過實驗研究了冰球在流動水中的融化和傳熱過程,得到了球體的總融化速率和周圍流體的流動特性.Mwansa等人[3]對Cu-Ni顆粒在Cu2S熔融液中的熔化過程進行實驗研究,得到了自然對流換熱條件下顆粒的熔化過程.Argyropoulos 等人[4-5]測量了不同情況下不同金屬球體在他們過熱熔體中的熔化時間,得到了熔化時間在對流換熱條件下的無量綱的表達式.然而,由于成本高、不確定性強,采用實驗方法對相變系統進行研究難度較大.在這種情況下,數值方法能夠對熔化過程中的熱傳遞特性進行深入研究.
關于這方面已經有了一些研究結果,利用有限體積法,Kumar等人[6]擬合了球狀顆粒在同一材料熔池熔化的時間與雷諾數、斯蒂藩數和普朗特數的關系,但沒有考慮溫度變化引起的自然對流以及凝固殼形成階段的影響.Argyropoulos等人[7]通過數值方法對形成于冷鋼柱表面的鋁殼的凝固和熔化速率進行了研究,但中心鋼柱沒有參與相變過程.Melissari等人[8]開發的數學模型,用于預測具有不同普朗特數的金屬球狀顆粒在熔體中的熔化時間,但對流體的流動引起的球體不均勻熔化卻沒有考慮.鑒于常溫球狀顆粒在浸入過熱液態金屬后首先在其表面形成凝固殼,同時其熔化過程受熔體強迫對流強度的影響,本文建立固態球狀顆粒在流動熔體中的熔化模型,揭示對流換熱下顆粒相變過程及規律.
1 數學模型
由Hao[2]等的實驗研究可知,顆粒在熔化過程中以直徑處水平面為對稱軸呈對稱分布,因此建立一個二維軸對稱模型,以一個球截面以及一定范圍流體域作為計算域.解決的物理問題可描述為直徑為D的球狀金屬顆粒置于具有一定流速的過熱熔體中,顆粒初始溫度遠低于其熔點.顆粒球心位于距流體入口4D處,為防止回流的影響,出口位于流體下游距離球體中心8D處.過熱熔體掠過冷金屬顆粒表面,使其熔化.所建立的計算域模型示意圖及顆粒區域局部網格如圖1所示.
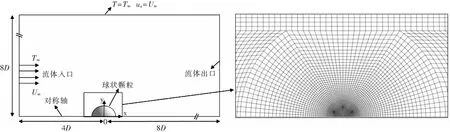
圖1 計算域模型示意圖Fig.1 Schematic diagram of calculation domain for the model
1.1 控制方程
綜合考慮流動、傳熱以及熔化問題,采用固定網格均相法建立數學模型.掠過半球的流體視為層流不可壓縮牛頓流體,連續性方程可表示為:
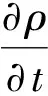
(1)
其中:v為速度分量,m/s;ρ為流體密度,隨溫度變化.
動量方程為:
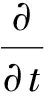
(2)
其中:SB為溫度變化引起的浮升力動量源項,可表示為:
SB=ρ0β(T-T0)g
(3)
Sp為采用多孔介質假設,依據達西定理,考慮凝固對流動的阻礙作用引入的動量源項,可表示為:

(4)
糊狀區常數:
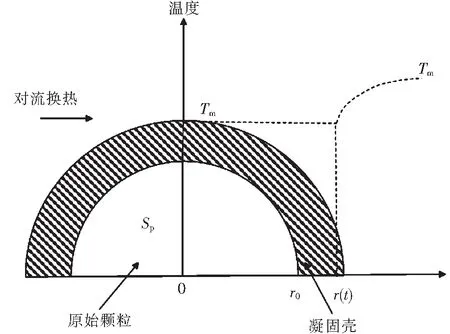
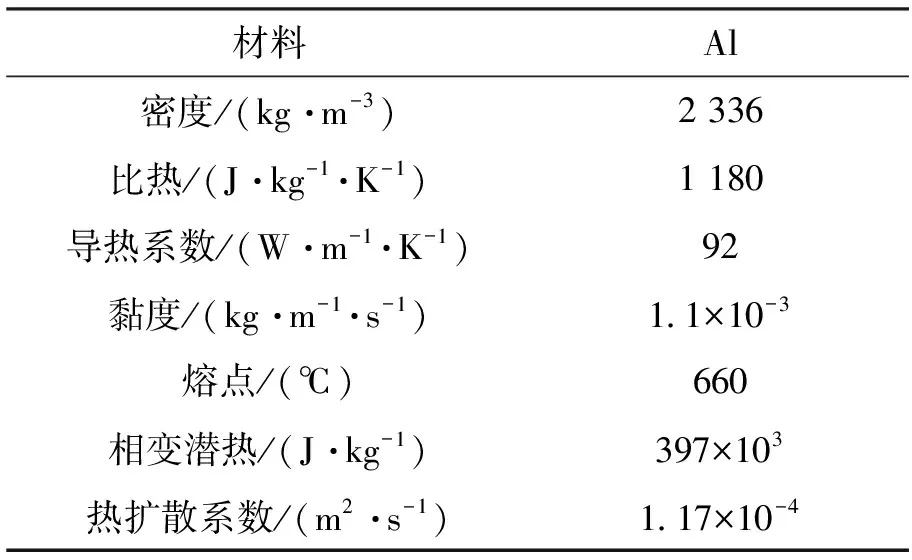
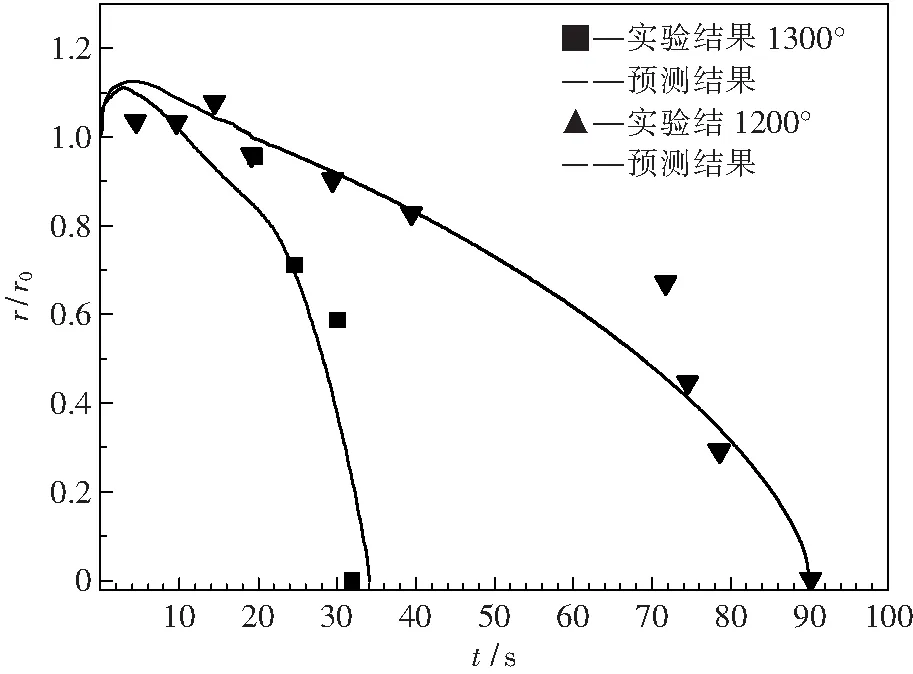
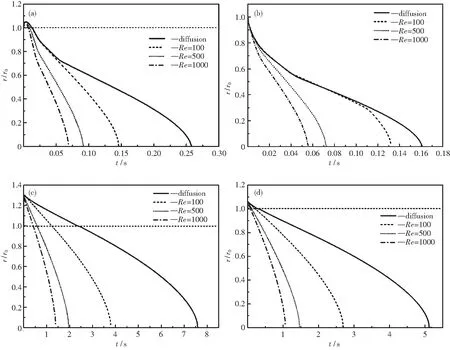
Amush=1.016×106kg/sm3
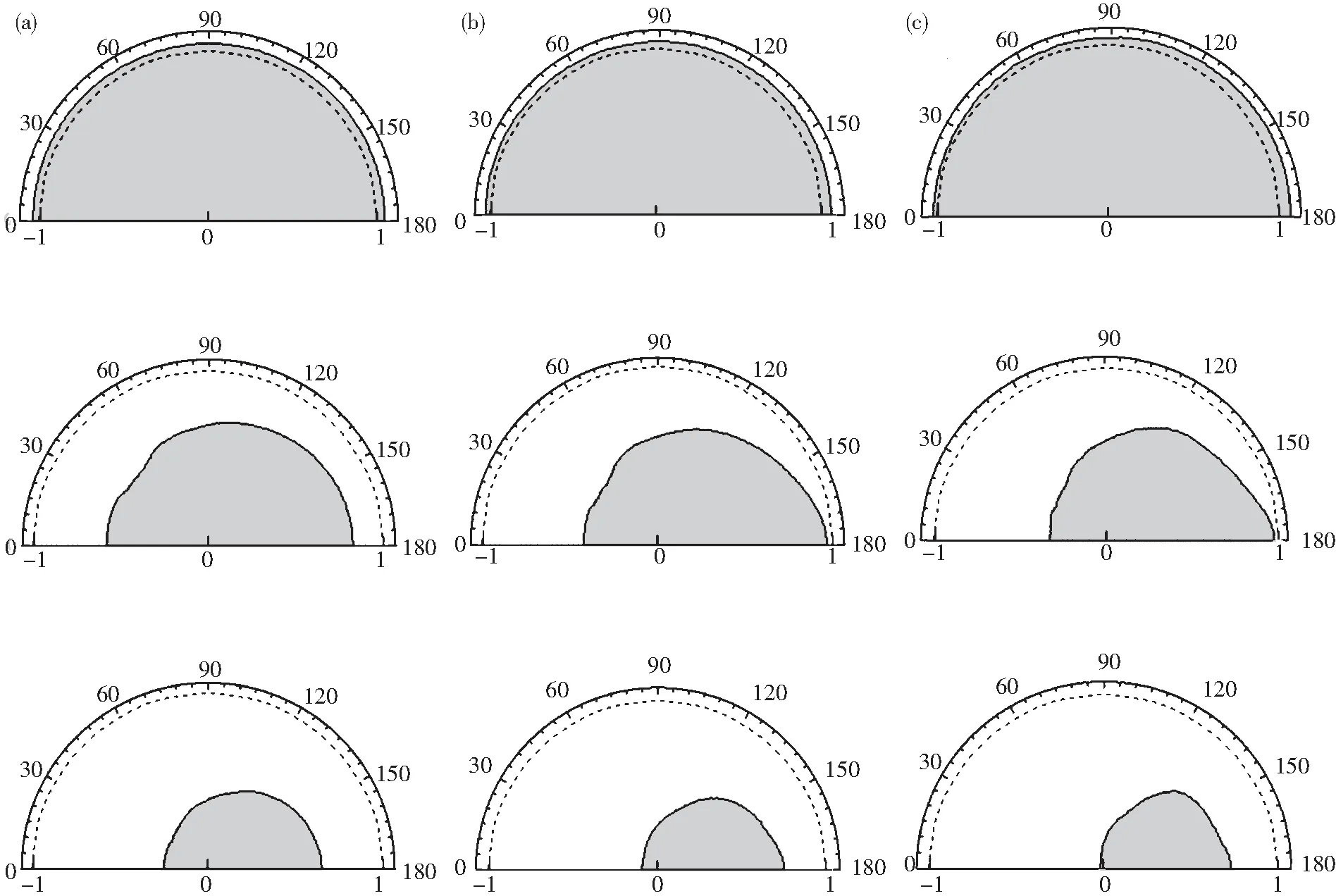
其中:g為顆粒與流體交界處糊狀區的液相率,T 在TTl時,g=1. 凝固與熔化過程中伴隨放熱與吸熱,為準確描述相變過程,采用焓法進行描述[9-10].控制方程為: (5) (6) 其中keff為導熱系數,L為相變潛熱. 左側熱熔體入口x=-4D, 0 vx=u∞,vy=0,T=T∞ 右側熱熔體出口x=8D, 0 中心對稱軸 ,y=0, -4D 邊界熔體自由發展區y=8D, -4D vx=u∞,vy=0,T=T∞ 初始時刻當t=0時, 在固體球狀顆粒區域, T=T0,vx=vy=0 在流動熱熔體區域, T=T∞,vx=vy=0 本文以半徑為1 mm鋁制小球浸入過熱鋁液中的模型為基礎,建立固態球狀顆粒在流動過熱熔體中的傳熱、流動以及相變模型.采用有限體積法,將方程(1)(2)(5)進行耦合計算,應用SIMPLE算法求解.控制方程采用二級迎風模式進行離散.熱流體掠過固態球狀顆粒時傳熱過程示意圖如圖2所示,在此過程中假設固體顆粒不隨流體運動. 計算采用商業軟件FLUENT 12.0, 圖2 顆粒與過熱熔體傳熱示意圖Fig.2 Schematic diagram of the heat transfer between the melting particle and the fluid 計算過程中時間步長為 0.0001 s;為保證結果準確,連續、動量方程殘差收斂至10-6,能量方程收斂至殘差為10-8.計算所采用的材料熱力性質如表1所示. 表1 材料的熱力性質 利用該模型計算固態Cu-Ni顆粒浸入液態Cu2S過程中顆粒半徑隨時間的變化.其結果與文獻[11]中實驗結果進行對比,液態Cu2S溫度分別為 1 200° 和 1 300°,固體球狀顆粒的初始溫度為 800°.由圖3所示,通過模型計算得到的結果與實驗吻合得較好,說明了該模型的準確性.這里顆粒半徑是等效半徑,即通過計算固態區域總體積反推出顆粒半徑: (7) (8) 圖3 模型驗證示意圖Fig.3 Verification of the model 利用驗證的模型對不同工況下球狀金屬顆粒在過熱熔體中的熔化規律進行研究.主要研究了顆粒初始溫度,熔體過熱度以及流動強度對顆粒相變過程的影響.由于球狀顆粒初始溫度低于金屬熔點,在浸入過熱熔體中之初,會在其表面形成一定量的“凝固殼”,待其溫度達到熔點后,由外至內開始熔化.在本模型中,以h=hs處為液態與固態的交界處,通過跟蹤該界面,可得到顆粒浸入過熱鋁液后完整的相變過程以及顆粒完全熔化所需時間.圖4所示為具有不同初始溫度的顆粒浸入具有不同過熱度的熱流體時顆粒半徑隨時間的變化規律,這里采用的半徑為等效半徑,計算公式為: (9) 由結果可知,在顆粒初始溫度為20℃,金屬熔體過熱度為30℃時,初期形成的“凝固殼”最大,可達1.3r0. 最大“凝固殼”厚度隨初始溫度的增大而減小,隨熱流體過熱度的增大而減小,隨流動強度的增大而減小.在同一工況下,流動強度對最大“凝固殼”厚度影響不顯著.同時,顆粒完全熔化時間隨初始溫度的增大而縮短,隨熱流體過熱度的增大而減小,隨流動強度的增大而減小. 圖4 顆粒有效半徑隨時間變化Fig.4 Variation of non-dimensional effective radius with time (a) —ΔT=300 T0=20℃; (b)—ΔT=300 T0=500℃; (c)—ΔT=30 T0=20℃; (d)—ΔT=30 T0=500℃ 圖5 不同工況下顆粒熔化時間隨熔體流動強度的變化Fig.5 Melting time of the particle as a function of Reynolds number under different conditions 在掠過顆粒表面的過熱熔體有流動的情況下,顆粒熔化過程明顯不同于其浸于靜止流體中的情況.隨著流動強度的增大,顆粒熔化速度明顯提高,完全熔化時間顯著縮短.這是由于隨著熔體流動強度的增大,顆粒外部對流換熱量顯著增大,較大的對流換熱量減小了其與冷顆粒吸收熱量之差[11],從而在熔化之初形成較少的“凝固殼”.流動強度對球狀顆粒與熱流體之間的換熱的影響體現于顆粒完全熔化所需時間.圖5所示為同一球狀顆粒的完全熔化時間隨過熱流體流動強度變化的規律,流動強度用無量綱數Re表示.由數值結果分析發現,不同流動強度下該規律的形式基本一致.根據以上結果,可擬合熱熔體流動強度Re與顆粒熔化時間tm的函數關系,得到: (10) 由圖可知,擬合曲線與數值結果變化趨勢基本一致,但在雷諾數較小時,擬合結果略低于數值結果.由數值結果可得到不同工況下的常數C1、C2,從而可應用到預測更多工況下顆粒的熔化時間. 如圖6所示為固態球狀顆粒在形成外部凝固殼厚度最大時刻、以及整體熔化初期、熔化中期以及熔化末期的瞬態顆粒形態.圖中虛線表示顆粒原始尺寸,即r0=1 mm,灰色區域為固態區.由圖可知,受流動影響,熔化初期形成的凝固殼與后期熔化呈不均勻形態,即整體不再保持規則球狀.距離左側流體入口較近處即球體前端形成的凝固殼較少.雖然球體與流體交界處導熱量均勻,但由于球體前端對流強度較大[12],因此與球體冷卻量之差減小,形成的凝固殼厚度減小.同理,當流體速度增大時,對流換熱量增大,形成較少的“凝固殼”.整體看來,在顆粒前端距離上游較近處以及其后端尾跡處熔化較快,邊緣熔化較慢.當流體在流過球形顆粒時,由于黏性在其表面形成邊界層,在邊緣中部靠后分離,而后由于較大的流速,在尾端形成漩渦,加快了對流換熱,因此尾部熔化較快.在假設顆粒各方向導熱量相同時,這也說明在與水平不同夾角處,過熱熔體與固體顆粒之間存在不同的對流換熱系數. 圖6 不同流動強度下顆粒形態隨時間變化Fig.6 Variation of non-dimensional effective radius with time (a) —Re=100; (b)—Re=500; (c)—Re=1000 針對金屬顆粒在過熱熔體中的熔化問題,建立了該過程的數學模型,并通過該模型求解不同工況下金屬顆粒在流動熔體中熔化規律,得到如下結論: (1) 球狀金屬顆粒在過熱熔體中的熔化速度受其初始溫度,熔體過熱度以及熔體流動強度的影響.最大“凝固殼”厚度隨初始溫度的增大而減小,隨熱流體過熱度的增大而減小,隨流動強度的增大而減小. (2) 由數值分析結果,球狀顆粒熔化時間與熔體流動強度Re之間的關系可表示為: (3) 與浸入靜止熔體中不同,在流動熔體中,顆粒熔化呈現非均勻性,具體地說,在前端與尾跡處熔化速度較快而中間邊處熔化速度較慢. [1] Lao Y L. Heat transfer characteristics of melting Ice, spheres under forced and mixed convection[J]. Journal of Heat Transfer, 2002, 124(124): 891-903. [2] Hao Y L, Tao Y X. Melting of a solid sphere under forced and mixed convection: flow characteristics[J]. Journal of Heat Transfer, 2001, 123(5): 937-950. [3] Mwansa J C, Warner N A. Natural convective heat transfer between single ore pellets and molten copper-nickel matters[M]. African Mining, London, 1987: 253-266. [4] Argyropoulos S A, Mikrovas A C. An experimental investigation on natural and forced convection in liquid metals[J]. International Journal of Heat & Mass Transfer, 1996, 39(3): 547-561. [5] Argyropoulos S A, Mikrovas A C, Doutre D A. Dimensionless correlations for forced convection in liquid metals: Part I. single-phase flow[J]. Metallurgical and Materials Transactions B, 2001, 32(2): 239-246. [6] Kumar A, Roy S, Kumar A, et al. Heat transfer characteristics during melting of a metal spherical particle in its own liquid[J]. International Journal of Thermal Sciences, 2010, 49(2): 397-408. [7] Sukhram M, Argyropoulos S A. Solidification and melting of aluminum onto circular cylinders under forced convection: experimental measurements and numerical modeling[J]. Metallurgical and Materials Transactions B, 2014, 45(5): 1723-1738. [8] Melissari B, Argyropoulos S A. Development of a heat transfer dimensionless correlation for spheres immersed in a wide range of Prandtl number fluids[J]. International Journal of Heat & Mass Transfer, 2005, 48(21-22): 4333-4341. [9] Swaminathan C R, Voller V R. A general enthalpy method for modeling solidification processes[J]. Metallurgical Transactions B, 1992, 23(5): 651-664. [10] Swaminathan C R, Voller V R. On the enthalpy method [J]. International Journal of Numerical Methods for Heat & Fluid Flow, 1993, 3(3): 233-244. [11] Melissari B, Argyropoulos S A. Measurement of magnitude and direction of velocity in high-temperature liquid metals. Part II: Experimental measurements[J]. Metallurgical and Materials Transactions B, 2005, 36(5): 639-649. [12] Kumar A, Roy S. Melting of a solid sphere placed in an Infinite medium-effect of forced convection[J]. Numerical Heat Transfer Part A Applications, 2009, 55(6): 594-609. Amathematicalmodelofmeltingprocessforsphericalsolidparticlesinaflowingmelt Niu Ran, Li Baokuan, Liu Zhongqiu, Li Xianglong (School of Metallurgy, Northeastern University, Shenyang 11089, China) Aimed at the solid metal melting in the liquid melt, a mathematical model was built. The finite volume method was used to study the factors affecting the melting process of the spherical particle. The results indicated that the melting process is affected by the particle initial temperature, the melt superheat and the flowing strength of the liquid melt. The convection around the sphere has a big effect on the phase change process. From the solidification sheath formation on the melting process, there is an uneven situation. The melting rate on front and rear region is faster than that on edge of the particle. melting process; mathematical model; spherical solid particles 10.14186/j.cnki.1671-6620.2017.04.003 TF 703.4 A 1671-6620(2017)04-0250-06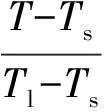
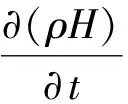
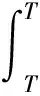
1.2 初始條件及邊界條件


2 計算方法
3 結果與討論
3.1 模型的驗證
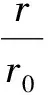
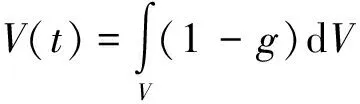
3.2 相變過程分析
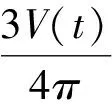
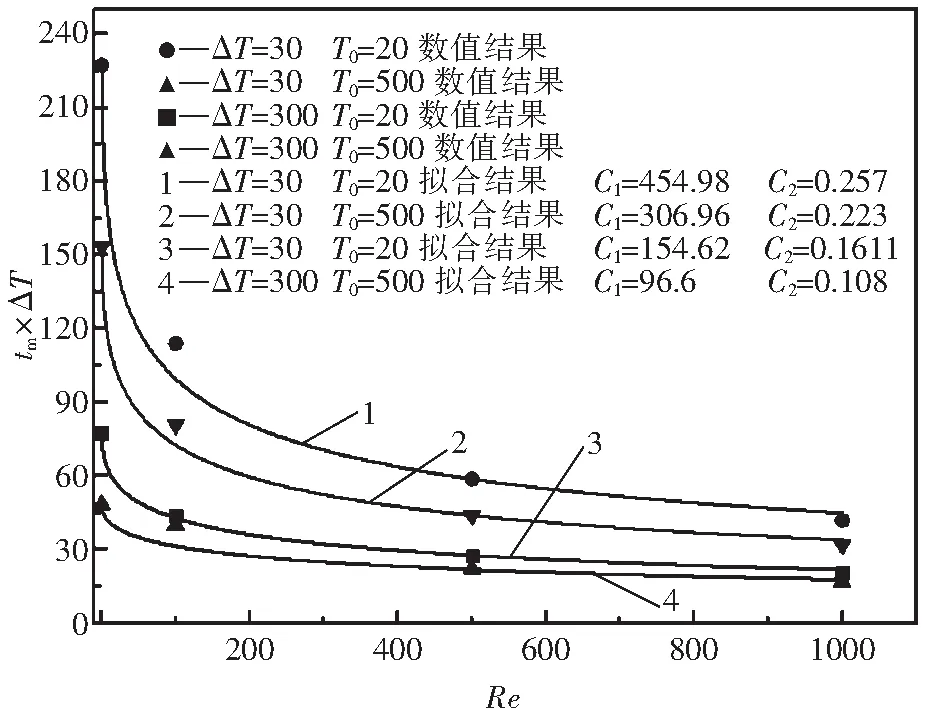
3.3 流動對相變的影響
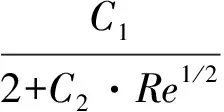

4 結 論