撥開迷霧,尋根溯源找模型
——排列組合問題淺談
■河南省商丘市第一高級中學 翟永恒
撥開迷霧,尋根溯源找模型
——排列組合問題淺談
■河南省商丘市第一高級中學 翟永恒
排列和組合是高中數學的一個難點,同學們都知道這類題需要借助數學模型進行解決。但是有一些創新題情景生疏,如同霧里看花不知如何下手。其實這類問題往往蘊含著一些經典模型,只需要找到它們的“題根”,從而順利轉化為某些經典模型進行解題。
題根1:(拿賀卡模型)有4位同學每人寫一張賀卡放在一起,然后每人拿一張賀卡,要求每人都不拿自己的賀卡,所有拿法總數是____。
解析:假設有甲、乙、丙、丁4人各寫一張賀卡,甲先去拿一個賀卡,有3種方法,假設甲拿的是乙寫的賀卡,接下來讓乙去拿,乙此時也有3種方法,剩下兩人中必定有一人自己寫的賀卡還沒有發出去,這樣兩人只有1種拿法,總的拿法為3×3×1×1=9(種),故答案為9。
例1 如圖1,用四種不同顏色給圖中的A,B,C,D,E,F六個點涂色,要求每個點涂一種顏色,且圖中每條線段的兩端涂不同的顏色,則不同的涂色方法種數共為( )。
A.2 8 8 B.2 6 4 C.2 4 0 D.1 6 8
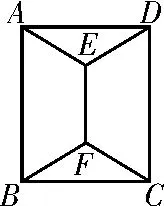
圖1
例2 有4位同學在同一天的上午、下午參加“身高與體重”,“立定跳遠”,“肺活量”,“握力”和“臺階”五個項目的測試,每位同學上午、下午各測試一個項目,且不重復。若上午不測“握力”項目,下午不測“臺階”項目。其余項目上午、下午都各測試一人,則不同的安排有____種(用數字作答)。
解析:先安排4位同學參加上午的“身高與體重”、“立定跳遠”、“肺活量”、“臺階”測試,共有種不同的安排方法;接下來安排下午的“身高與體重”、“立定跳遠”、“肺活量”、“握力”測試,假設A、B、C同學上午分別安排的是“身高與體重”、“立定跳遠”、“肺活量”測試,若D同學選擇“握力”測試,安排A、B、C同學分別交叉測試,有2種;若D同學選擇“身高與體重”、“立定跳遠”、“肺活量”測試中的1種,有種方式,安排A、B、C同學進行測試有3種。根據計數原理共有安排方式的種數為
題根2:(插空模型)有4名男生和2名女生站成一排,要求女生不相鄰,則共有____種站隊方法。
例3 在一次文藝演出中,需要給舞臺上安裝一排完全相同的彩燈1 5只,現以不同的亮燈方式來增加舞臺效果,設計者按照每次亮燈時恰好有6只是關著的,且相鄰的彩燈不能同時關掉,兩端的彩燈必須要亮的要求進行設計,則不同的亮燈方式共有____種。
解析:問題實際只需要將9只亮的彩燈看作題根2中的男生,6個關的彩燈看作題根2中的女生,即可視為不相鄰模型,由于兩端的彩燈必須亮,所以共有=2 8(種)亮燈方法。
例4 顯示屏上有一排共7個小孔,可顯示0或1,若每次顯示其中3個孔,但相鄰的兩個孔不能同時顯示,則該顯示屏能顯示的信號種數為( )。
A.4 8 B.5 6 C.6 0 D.8 0
通過以上例題可以發現,雖然排列組合的問題情境不斷推陳出新,乍一看可能無從下手,但仔細分析會發現實際上仍是經典模型的應用,我們只需追根溯源,即可順利借助經典模型進行求解。
(責任編輯 王福華)

