等誤差步長法計算點云數控加工刀軌方法研究

（蘇州科技大學 機械工程學院，蘇州 215000）

0 引言

走刀步長即同一條刀具軌跡上相鄰兩刀位點間的距離，步長的大小與刀軌的逼近精度緊密相關。步長規劃方法主要有等距離法、篩選法和等誤差步長法。等距離法采用相等的距離對刀軌進行插值，為滿足逼近誤差，取值較為保守，從而生成較多的冗余刀軌。篩選法先運用等距離步長法獲取密集的刀位點，在滿足誤差的前提下，刪除一些冗余刀位點以減少數量。等誤差步長法通過對刀位點進行逐點計算，使逼近誤差均為最大允許值（閾值），從而步長最大、刀位點最少。直接對點云生成數控加工刀軌，避免了將點云擬合成曲面模型，可大幅縮短刀軌生成時間，為此許多學者對此進行了研究。

點云生成刀軌方面，最早由Tskuasa[1]提出一種用三坐標測量機測量點云直接生成刀軌的方法，該方法將實物表面測量的點作為刀位點，但刀具半徑必須等于測量頭的半徑。Lin[2,3]、楊建中[4]、Yau[5]等提出了運用Z-map法對點云生成粗加工刀軌，一般過程是先構造Z-map模型，獲取加工平面上的切削區域，最后生成刀軌。Park[6,7]等系統地研究了點云的粗加工、精加工、清根加工問題，提出的方法無需建構刀位面，可省去計算多面體間布爾運算等許多復雜運算，但是加工精度問題一直難以保證。吳福忠[8]對規則點云等距獲得殘留高度面和刀位面，分別與刀具包絡面求交計算出殘留高度點和等殘留高度刀軌。本文作者[9]避免對點云重構曲面或等距，提出了直接在球頭刀切削輪廓上搜索殘留高度點和計算下一行等殘留高度刀軌的方法。等誤差步長方面，趙世田等[10]采用黃金分割法在刀觸點曲線上取點計算誤差以提高最大弓高誤差精度，黃琴、楊旭靜等[11]通過控制線性誤差和轉動誤差來優化刀軌上刀觸點的位置分布。本文作者[12]避免對點云重構曲面，對截面線上的刀觸點依次構造半徑為誤差閾值的圓及其切線，通過限定刀軌范圍求出等誤差步長刀軌。Lin、Fu等[13]對參數曲面提出了一種等逼近誤差的刀軌規劃方法，在兩個刀觸點之間構造多個射線以計算加工誤差，并通過增減參數量搜索等誤差刀觸點。

現有方法大多采用近似的求解，所計算出的刀軌實際逼近誤差接近但并不完全等于閾值，提高精度需要大量計算，難以高效求出理想的等誤差刀軌。為此，本文以點云為研究對象提出一種等誤差步長刀軌生成方法，首先將點云劃分到立方體小柵格，采用等行距、等步長計算出初步刀位點，然后對每一行刀位點進行篩選，獲取接近理想誤差的刀位點，并獲取鄰域刀位點，計算出誤差等于閾值為的刀位點，并求出相應的刀軌，最后給出一種計算出誤差等于閾值的刀位點的方法。

1 點云數據預處理

點云包含海量散亂點，將點云劃分到柵格中以便于管理和提高算法效率。獲取所有數據點的最大最小坐標值xmax、ymax、zmax、xmin、ymin、zmin，以此創建一個與坐標軸平行的長方體包圍盒。立方體柵格邊長mcell一般取刀具半徑的0.3～0.5倍，柵格在3個方向上的個數可由式(1)求出，構造三維數組Cell[Xnum][Ynum][Znum]，任意點p(x,y,z)所在的柵格序號可由式(2)求出，最后獲取每個柵格包含的點。

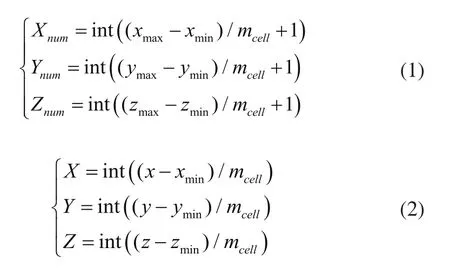
2 刀具路徑規劃

2.1 獲取初始刀位點

本文選擇常用的等間距行切法進行刀軌規劃，設Y正方向為行距方向，X正方向為進給方向，第i行第j個刀位點為已知行距W和步長ΔL可由式(3)計算出的x、y坐標，進而可求出刀具在XY平面上的邊界坐標其中R為刀具半徑，將其帶入式(2)求出相應的柵格序號Xl、Xr、Yu、Yd，獲取所有序號滿足的非空柵格，所包含的點記為{pi,j}。

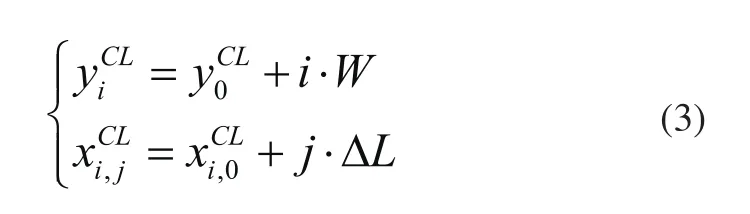
按照以上方法可求出所有刀位點的坐標。

2.2 等誤差步長法計算刀位點

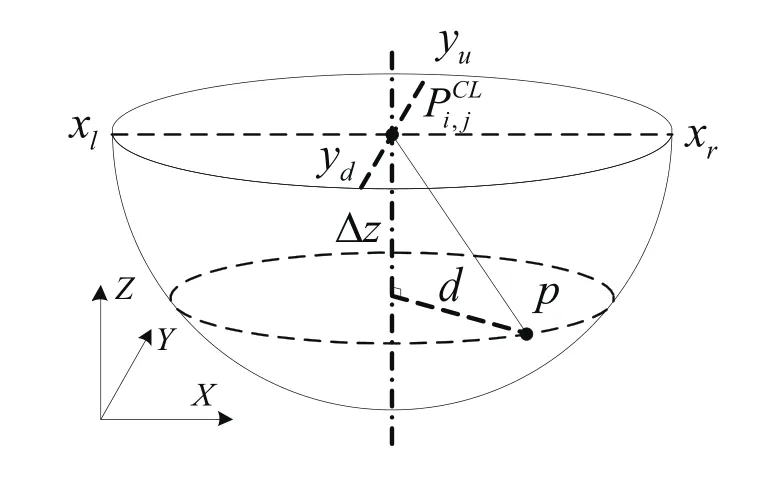
圖1 刀具和刀位點示意圖

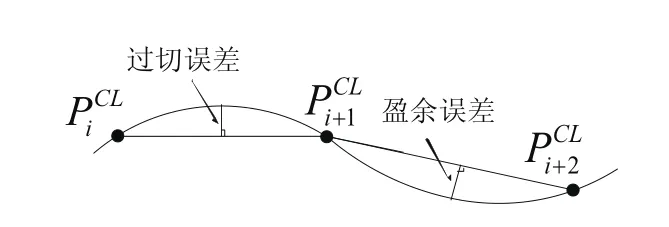
圖2 過切容差和盈余容差示意圖

如圖2所示，步長方向的誤差分為過切誤差和盈余誤差，等距離法通過選取保守的步長、篩選法通過刪除冗余刀位點的方法使刀軌誤差小于閾值，但都沒有達到步長最大化、誤差均勻。本文提出一種等誤差步長法計算刀位點，首先計算出誤差最接近閾值的刀位點，在其附近以小步長計算出新的鄰域刀位點，以此為圓心，以過切、盈余誤差閾值e1、e2為半徑作圓，對半徑為e1的圓計算下切線、e2計算上切線，計算鄰域刀位點到切線距離的最大值，若小于等于e1(或e2)，計算切線與刀位點連線的交點，則切線與刀位點連線的交點與開始點連線作為刀軌時，其誤差為閾值。然而交點只是刀軌插值的結果，還需要對交點進行調整才能使刀具與點云相切。

Step1：計算誤差最接近閾值的刀位點。

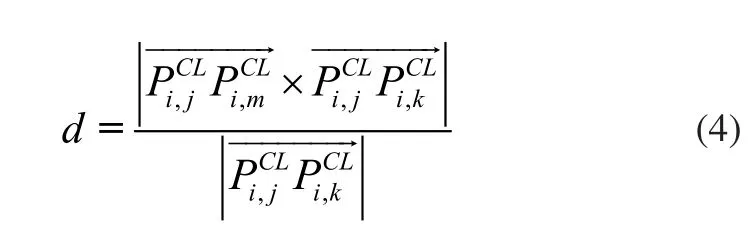
本文通過室內模型試驗，以福建省龍巖地區常見的覆蓋型巖溶土洞為研究對象，通過設計不同工況，改變不同樁長研究了兩種不同工況下的復合地基的變形特性，得到以下結論：

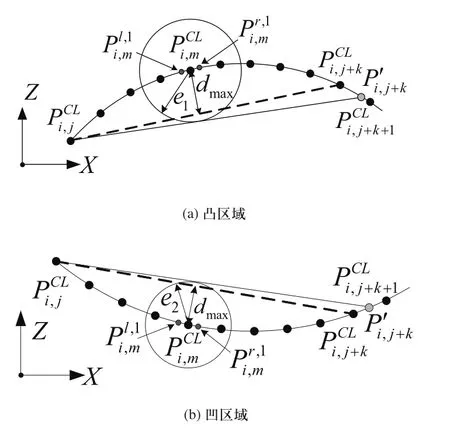
圖3 計算誤差示意圖

Step4：計算滿足等誤差要求的刀位點。

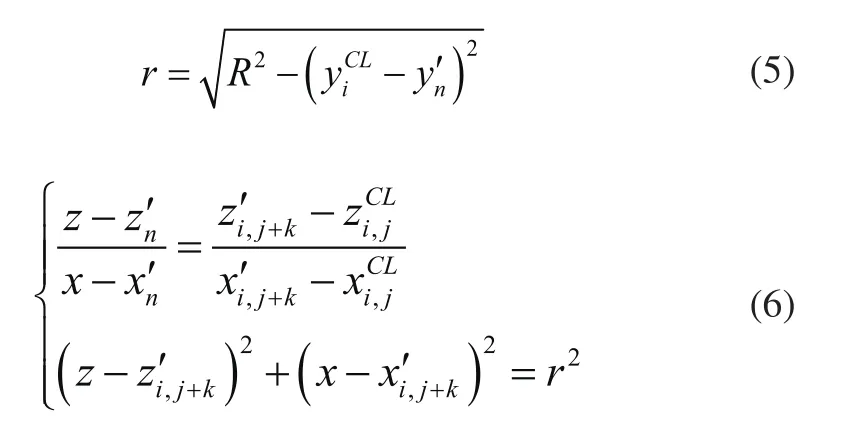
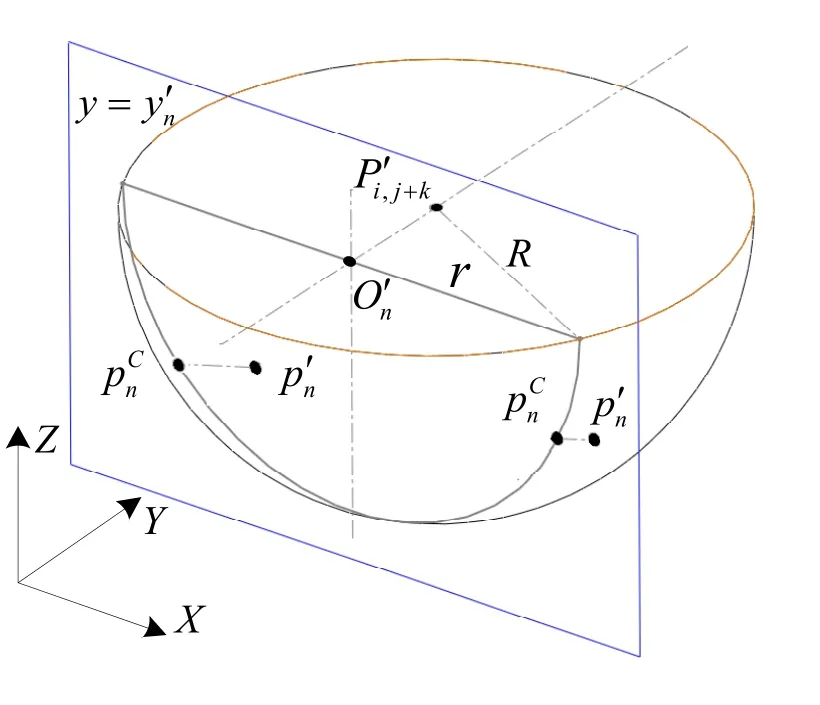
圖4 計算刀位點偏移量示意圖

按照以上方法，即可求出所有等誤差刀位點。

3 算例

圖5所示的點云模型為曲面的掃描點集，包含401153個點，包圍盒大小為330×354×85。加工參數選取方面，球頭刀直徑為20，行距為5，初始步長為0.5，過切、盈余誤差閾值均為0.01，生成刀軌如圖6所示，共67行。選取3行與篩選法生成的刀軌進行比較，圖7和圖8分別是步長篩選法和本文算法生成刀軌的部分誤差分布，可以發現本文算法求出的刀軌誤差均勻而步長篩選法的誤差不均勻。表1給出了兩種方法生成的刀軌包含刀位點數量的比較，可發現在刀位點數量較多的行（其表面曲率變化大），本文算法求出的刀位點數量降幅更大，所有行刀位點總數比篩選法減少了約17%。

圖5 點云模型

圖6 生成的刀軌

4 結論

本文給出了運用等誤差步長法計算點云刀軌的方法，通過篩選法初步確定最大誤差發生的位置，然后通過插值求出精確值，確保了效率和精度；通過構造誤差閾值圓并求切線作為刀軌方向，確保了刀軌的逼近誤差等于閾值，并求出了精確的等誤差刀位點，使步長達到理論最大值。所提出的方法能夠直接對點云生成等誤差刀軌，實現誤差等于閾值，最小化刀位點數量。在未來的研究中，可著重研究根據局部輪廓直接計算等誤差刀位點的方法，以進一步減少計算量。

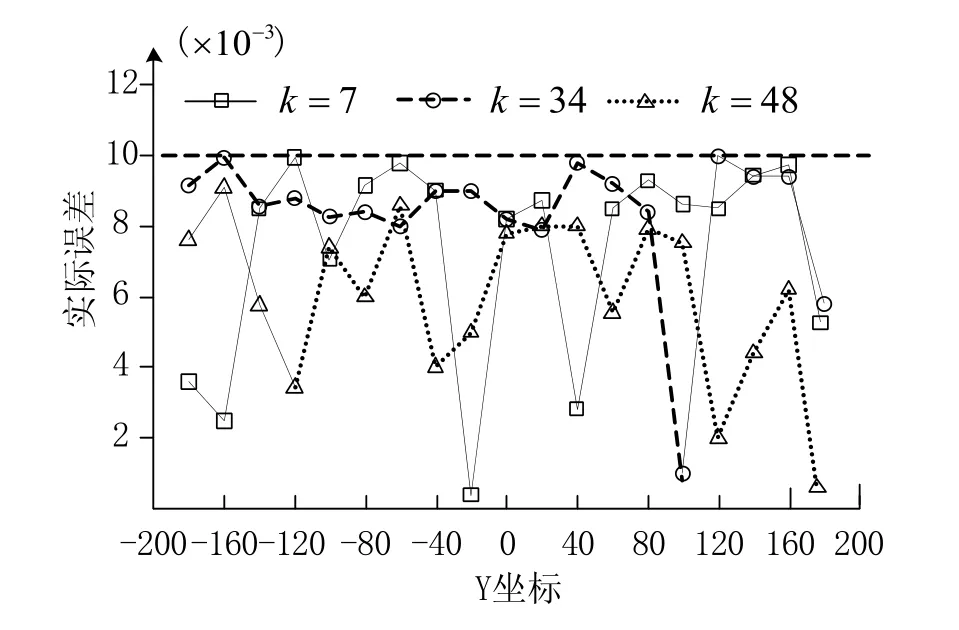
圖7 步長篩選法對應的第k行刀軌誤差分布

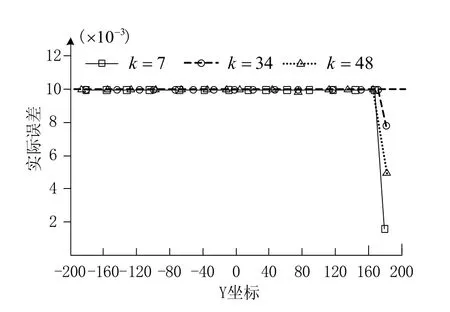
圖8 本文等誤差步長法對應的第k行刀軌誤差分布

表1 刀位點數量比較

[1]Tsukasa K, Takeshi K, Katsumas S. Machining system based on inverse offset method[J].Journal of Precision Engineering,1988,54(5):971-976.

[2]Lin AC, Liu HT. Automatic generation of NC cutter path from massive data points[J].Computer Aided Design,1998,30(1):77-90.

[3]Lin AC, Lin SY. Computer-aided mold engraving: from pointdata smoothing, NC machining, to accuracy checking[J].Journal of Materials Processing Technology,1999,86(3):101-114.

【】【】

[4]楊建中,王啟富,黃正東,陳剛.組合曲面的粗加工刀軌算法[J].計算機輔助設計與圖形學學報,2006,18(2):295-301.

[5]Yau HT, Hsu CY. Generating NC tool paths from random scanned data using point-based models[J].The International Journal of Advanced Manufacturing Technology,2009,41(9-10):897-907.

[6]Park SC,Chung YC.Tool-path generation from measured data[J].Computer Aided Design,2003,35(5):467-4[4]75.

[7]Kim DS,Jun CS,Park SC. Tool path generation for clean-up machining by a curve-based approach[J].Computer-Aided Design,2005,37(9):967-973.

[8]吳福忠.測量點數據等殘留高度刀具路徑規劃[J].計算機輔助設計與圖形學學報,2007,19(12):1618-1623.

[9]Liu W, Zhou LS, An LL. Constant scallop-height tool path generation for three-axis discrete data points machining[J].The International Journal of Advanced Manufacturing Technology,2012,63(1-4):137-146.

[10]趙世田,趙東標,付瑩瑩.自由曲面加工刀具路徑生成高精度變步長算法研究[J].機械科學與技術,2010,29(1):32-35.

[11]黃琴,楊旭靜,鄭娟.三角網格曲面加工刀具路徑生成等誤差步長算法研究[J].機械科學與技術,2015,34(9):1370-1374.

[12]劉威,周來水,安魯陵.截面線等誤差步長法計算點云刀具路徑規劃[J].機械科學與技術,2013,32(6):824-828.

[13]Lin ZW,Fu JZ,Shen HY.An accurate surface error optimization for five-axis machining of freeform surfaces[J].The International Journal of Advanced Manufacturing Technology,2014,71(5-8):1175-1185.