一類變分問題在中學物理課外教學中的嘗試

蔡子星

(北京質心教育科技有限公司，北京 100088)

變分法為理論力學中的歐拉-拉格朗日方程提供了基礎的數學形式，是現代物理學的常用的數學工具。其理論本身因應用廣泛、形式簡約，被作為本科生必修內容。由于理解變分法本身并不涉及復雜的微積分運算，同時理解變分法對清晰地認知一大類問題的物理圖像很有幫助，因此在中學生物理競賽大綱添加了微積分的要求以及大學先修課不斷普及的情況下，將變分內容作為對部分有特長的學有余力的中學生的補充課外教學材料引入教學實踐，成了一種可能的嘗試。

拋開變分問題嚴格的定義不談，狹義的變分問題可以這樣形象的理解(嚴格的數學定義可以參考文獻[1])。令

其中，y(x)是定義在[x1,x2]上的可導函數；I(y)是從滿足定義的函數y(x)到實數域上的映射。當y取到y(x)和其靠近的函數y(x)+δy(x)的時候，I的值變化δI相比δy是一個“高階小量”，我們就記δI=0，表明y(x)是I的一個極值點。

一類物理問題都可以用變分進行表述，比如連續體靜力平衡時勢能取極值，邊界固定的肥皂泡會形成面積最小形態，幾何光學中光走光程極值路徑，在固定的勢場下一個經典粒子的真實路徑會使得作用量取極值。本文就針對這個例子進行討論，并給出解答和指出這幾個模型中一些細節上的差異。在教學實踐中，針對這幾個問題，從建立模型，尋找對稱性，尋找約束條件，類似遷移等幾個方向啟發學生思維。

1 建立模型和解答

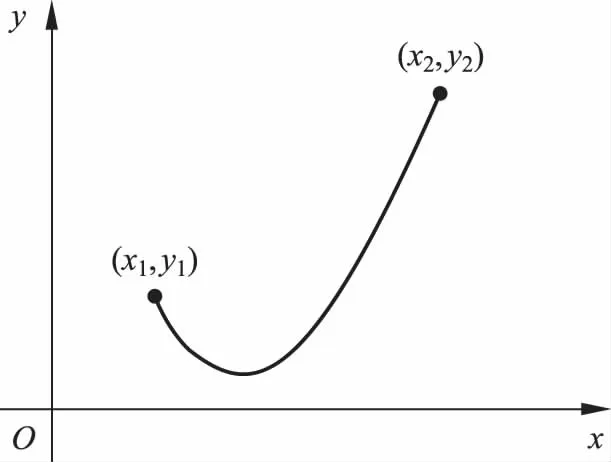
問題一將一根長度為L，單位長度質量為λ的柔軟的不可伸長的鏈條，在勻強重力場g中，兩個端點分別掛在坐標為(x1,y1)和(x2,y2)的點上，求平衡時繩子的形態y(x)。

(1)

滿足δI=0，y(x1)=y1;y(x2)=y2。這個問題被稱為懸鏈線問題。在許多理論力學書上都有討論[2]。

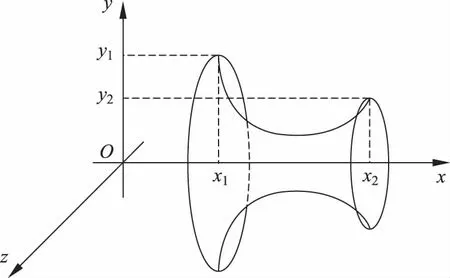
問題二在空間中有兩個圓環，都平行于y-z平面，圓心的x坐標分別為x1，x2，半徑分別為y1，y2。在兩個圓環之間有一層肥皂膜，在兩個圓環處開口，內外聯通。求平衡時肥皂膜的形狀。

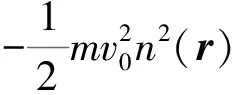
這4個問題的都可以歸結為解式(1)。代入歐拉-拉格朗日方程

得到

這個微分方程可以直接求解，得到

(2)

其中A,b是由初始條件確定的兩個待定常數。然而實際上不同中學生對微分方程的掌握程度有所不同，通過問題四的求解可以降低對微分方程要求。對于問題四，x方向動量守恒，在y方向受力為

α2y

由牛頓第二定律

α2y

這個方程的解是熟知的，為

y(t)=Aev0α t+Be-v0α t

在x方向上x(t)=vx0t，消去時間后得到軌道方程為

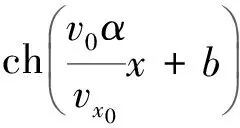
通過初始條件

vx0=v0αy1cosα

其中α是初態粒子運動方向和x軸夾角，以及y′(x1)=tanα，可以將軌道方程化成式(2)的形式。這樣問題一到問題四都可以通過簡單的運算得到。

2 對稱性的應用

問題四之所以比較簡單，原因在于使用了體系在x方向上的平移不變性，即x方向動量守恒。這個對稱性在式(1)中的表現在于F(x,y,y′)不顯含F(x)，這樣代入哈密頓方程有

(3)

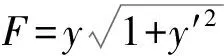
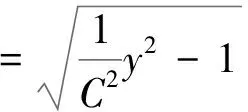
(4)

F(s)-F(0)=λgds(y(0)-y(s))

(5)

對從0到s這一段繩子水平方向受力平衡得到

F(s)cosα=F(0)

(6)

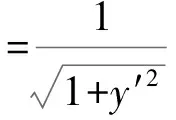
對于問題二可以對從x1到x之間的那一段液體沿x方向的受力平衡得到

2×2πycosα=C

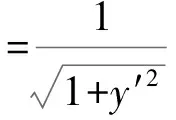
對于問題三就更加顯然，連續利用折射定律得到

n(y)cosα=C

即與式(3)等效。從這些例子我們可以看出，這些對稱性歸根結底來源于平移不變性，訓練學生發現這樣的對稱性也是重要的教學目的之一。

3 問題的推廣和約束條件的影響

如果仔細考慮這4個問題，可以發現問題一實際上和其他3個問題不同，因為在第一個問題中有約束條件繩長不變

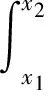
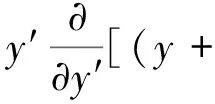
和原來的方程相比只需要讓y變成y+λ就得到解，也就是只是在y方向平移，對求解過程沒有太大影響。

θ

對應的哈密頓方程為

整理得到

于是軌跡方程為ρ=Ae±κ θ，其中A,κ是由初始條件確定的常數。然而這個解對問題一是無效的。例如拉格朗日乘子法得到

整理得到

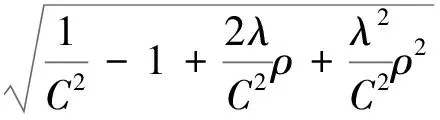
解得

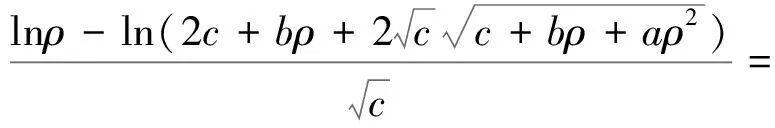
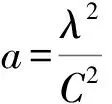
作為對學生的訓練，一方面可以啟發學生從平移不變性推廣到旋轉不變性，對問題一使用虛功原理和力矩平衡得到方程，對問題三利用正弦定理和折射定律得到方程，對問題四用角動量守恒加比奈方程得到方程。另一方面可以啟發學生看到約束條件對結果的影響。

4 結語

上面我們研究了力學、光學中的4個有趣的問題。這些貌似無關的問題，經由變分原理可以統一起來。我們從問題的建模，對稱性分析和約束條件的引入3個層面展示了變分原理在這些問題中的應用。內容上我們還設置了啟發引導的環節，這樣可以更好的提高學生的分析和思維能力。相信將這一物理學中的簡單而深刻的原理通過有趣的實例介紹給中學生，可以讓學生更早的接觸一些物理思維方面的高級內容，同時這一原理的美妙和威力也會給學生留下深刻印象，從而激發學生學習的興趣和鉆研精神。

[1] 老大中.變分法基礎[M]. 3版.北京：國防工業出版社，2015.

[2] 金尚年，馬永利.理論力學[M].2版.北京：高等教育出版社，2002.

[3] 玻恩M，沃耳夫E.光學原理[M].7版.楊葭蓀,等,譯.北京：電子工業出版社，2009.