鋼網格盒式結構多模態靜力彈塑性分析

雷宇龍，方祥位，孫濤

（后勤工程學院 軍事土木工程系，重慶， 401331）

0 引言

鋼網格盒式結構是一種新型大開間鋼結構節能住宅建筑體系，它是在鋼筋混凝土網格式框架結構體系[1-2]的基礎上研究提出的，其樓（屋）面結構是由大跨度鋼空腹夾層板構成，其豎向承重體系是由鋼網格式框架構成。該結構體系在開間和進深方向通過密排小型方鋼管柱或H型鋼柱，在層高內設置3～5道小型H型鋼梁（圖1），成功克服了常規鋼框架側向剛度差的缺點，又能實現大柱網大開間靈活布置；與常規剪力墻結構相比，其自重大大降低，地震作用變小，利于抗震設計[3]。同時，在工程實踐中，該結構的圍護墻體采用脫硫石膏、磷石膏等工業廢渣現場澆筑填充，具有節能環保、保溫隔熱的特點，既解決了環境污染問題，又能變廢為寶[4]。該結構體系實現了構件模塊工廠化生產，現場裝配化施工，既保證了工程質量，又縮短了施工工期。率高以及自由分割的優點非常符合住宅建筑人性化的要求[5]。目前，用于結構抗震性能研究的常見分析方法有：動力彈塑性分析、靜力彈塑性分析（即pushover方法），前者更接近于實際，但過于復雜不利于工程應用，因此規范普遍建議采用后者。Chopra和Geol于2002年在常規pushover分析方法的基礎上考慮多模態對分析結果的影響，提出了多模態靜力推覆分析法（MPA法），MPA法直觀上考慮高階振型的影響，目前被認為是有較好應用前景的方法[6]。本文針對一個12層的鋼結構住宅，分別建立鋼網格盒式結構和常規鋼框架結構三維有限元模型進行抗震設計，采用多模態靜力推覆分析法計算其罕遇烈度下的目標位移，對比研究兩種結構體系的抗震性能以及技術經濟性能。

1 多模態Pushover分析方法

圖1 鋼網格盒式結構實例

如上所述，該結構體系具有較高的抗側剛度，可以應用于小高層（45m以下）鋼結構住宅中，而且其室內無柱、空間利用

對于受高階振型影響較大的高層建筑，如果仍采用以一階模態為主的荷載模式（均勻荷載模式、倒三角模式），將無法對高階振型引起的中間層的剪力及層間位移角，做出合理的預測[6]。MPA分析法基于結構反應譜分析原理，將結構推覆至多階振型下的目標位移 （取質量參與系數達90%的前幾階振型）。在該推覆過程中，振型分布形式一般不變，可獲得每階振型下的結構響應，再通過SRSS法或CQC法來組合得到考慮高階振型效應的整體結構響應。

1.1 多模態Pushover分析步驟

（1）建立多自由度體系動力方程，進行模態分析，獲得結構動力特性，如前幾階周期、振型向量及振型參與質量等；

（2）針對每階振型，采用pushover分析方法，獲得控制層的基底剪力－位移曲線；

（3）基于等能量原則，對各振型對應的基底剪力－位移曲線折線化，獲得等效單自由度體系在各階模態下的譜加速度（A）位移（D）能力曲線，具體方法見1.2節；

（4）建立彈塑性反應需求譜，并轉換成譜加速度（A）－譜位移（D）曲線，具體方法見1.3節；

（5）將每階振型對應的能力譜同彈塑性需求譜畫在同一坐標系中，兩曲線交點可確定目標位移。各階模態反應平方和開方組合（SRSS）得到結構頂點位移和層間位移。

1.2 能力譜曲線

根據FEMA369[7]與ATC-40[8]，將獲得的控制層基底剪力－位移曲線轉化為譜位移Sd－譜加速度Sa曲線，即能力譜曲線。其中，振型參與系數Γn和等效模態質量分別為：

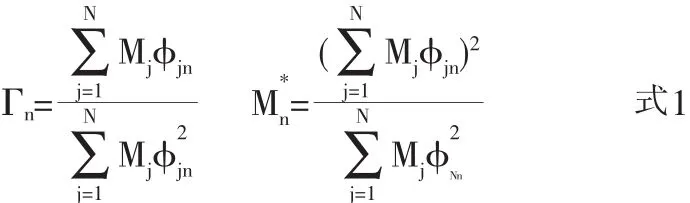
式中，Γn為第n階振型的振型參與系數；為等效單自由度體系的等效質量；Mj為結構第j層的樓層質量；φjn為第n階振型形狀向量的第j層分量；φNn為第n階振型形狀向量的控制層值；N為結構的總層數。

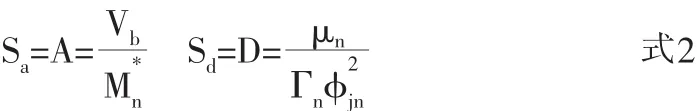
式中，Vb為結構的底層剪力值；μn為結構的控制層位移值；A、D分別為能力譜的加速度譜值和位移譜值。

1.3 彈塑性需求譜曲線

地震危險性分析可確定建造結構所在地的地震地面運動強度，再經過大量統計分析地震反應計算結果可得到結構需求譜曲線。為了近似考慮結構的非線性特征，基于改進能力譜法，許多學者采用折減系數R對彈性反應譜予以折減獲得彈塑性需求譜曲線，其中應用較多的是Vidic提出的計算公式[9]：

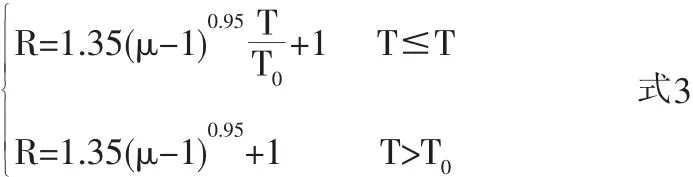
式中，T0=0.75μ0.2Tg。Tg—建筑場地的特征周期；μ為延性系數。

根據動力學原理[10]，彈性單自由度體系有以下近似關系：

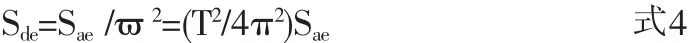
根據彈性反應譜和折減系數R，可以按下式求出彈塑性反應譜：

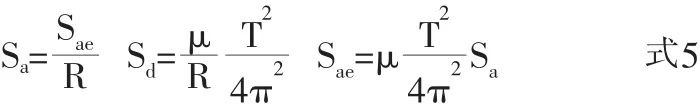
結合式1-式5，對《建筑抗震設計規范》中α曲線進行強度折減，得到彈塑性需求譜：

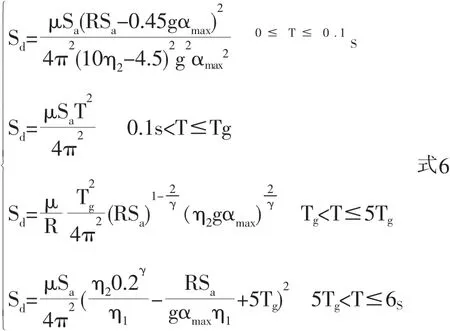
式中，T為自振周期；αmax為水平地震影響系數最大值；Tg為特征周期；γ為曲線下降段衰減系數；η1為直線下降段斜率調整系數；η2為阻尼調整系數。

通過不同延性系數折減，得到罕遇烈度下的彈塑性需求譜族如圖2所示。罕遇烈度地震影響系數曲線對應的αmax取 1.2。

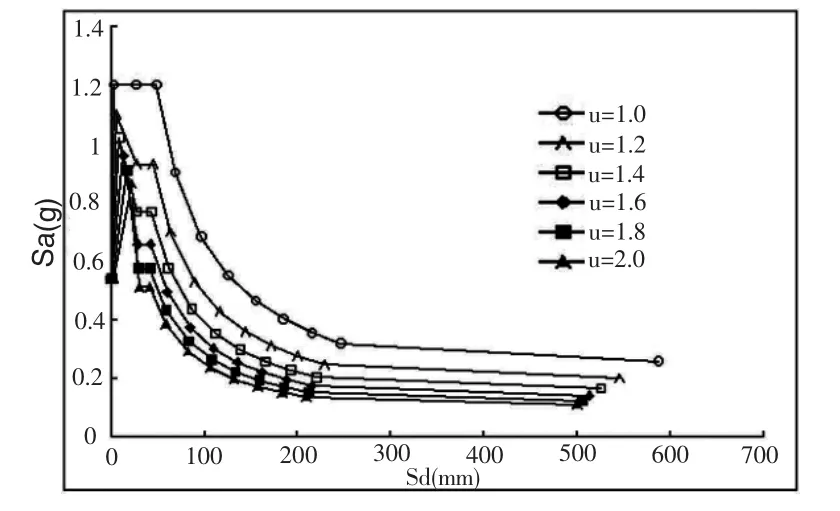
圖2 遇烈度彈塑性需求譜

2 分析模型

2.1 基本假定

（1）不考慮石膏對鋼網格盒式結構的剛度貢獻；（2）滿足力學平衡條件。

2.2 設計參數

模型為一座12層鋼結構住宅，幾何尺寸為10.5m×10.5m，層高為3.2m，分別建立常規鋼框架結構和鋼網格盒式結構模型。抗震設計參數：地震設防烈度為8度，設計地震加速度值為0.3g，設計地震分組第一組，場地類別為II類，場地特征周期為Tg=0.35s，結構抗震設計的阻尼比取ξ=0.04；靜力彈塑性分析的阻尼比取ξ=0.05；基本風壓取0.30kN/m2。結構荷載信息：樓面恒荷載4.0kN/m2，樓面活荷載2.0kN/m2，樓梯間均布活荷載6.0kN/m2，樓面活荷載1.5 kN/m2；屋面恒荷載6.0kN/m2，屋面活荷載0.5kN/m2；外墻線荷載取6.0kN/m，內墻線荷載取3.0 kN/m，層間梁及周邊空腹梁線荷載取2.0kN/m。

2.3 結構抗震計算

根據《鋼結構設計規范》（GB50017-2003）[11]、《高層民用建筑鋼結構技術規程》（JGJ99-98）[12]和 《建筑抗震設計規范》（GB50011-2010）[13]，采用PKPM軟件進行結構設計，構件截面尺寸如表1所示。

為了對比，對常規框架結構和鋼網格盒式結構分別進行模態分析，得出兩種結構的前8階振型周期（表2）。可以看出：框架結構剛度較小，周期較長；盒式結構剛度較大，周期較短。框架結構第一扭轉周期與第一平動周期比值1.8649/2.1618=0.863，低于規范限值0.9；盒式結構的第一扭轉周期與第一平動周期比值1.5246/1.8190=0.838，低于規范限值0.9。

設計地震作用下，框架結構最大層間位移角1/279，盒式結最大層間位移角1/360，均小于1/250。兩種結構樓層水平位移值與平均值之比均小于1.2，結構剛重比、最小地震力校核均滿足規范。

3 算例分析

本節針對1.3節中設計的兩種結構，采用MPA分析方法對比研究其抗震性能。兩種結構均只取y向振型質量參與系數達到90%的前幾階模態參與分析，框架結構和盒式結構均只需考慮1、4階模態。

3.1 基底剪力－位移曲線

針對兩種結構，分別進行所選各階振型下的pushover分析。采用Midas Gen[14]中的靜力非線性分析功能，考慮豎向施加重力荷載代表值作為初始狀態，進行多模態Pushover分析。結構控制層基底剪力－位移曲線見圖3，其中：一階模態荷載模式下，兩種結構控制層均為屋面；四階模態荷載模式下，框架結構控制層仍為屋面，盒式結構控制層為第五層。可見在一階模態和四階模態荷載模式下，盒式結構的側移剛度均大于框架結構；兩種結構體系在四階模態荷載模式下的結構側移剛度要遠大于低階振型。

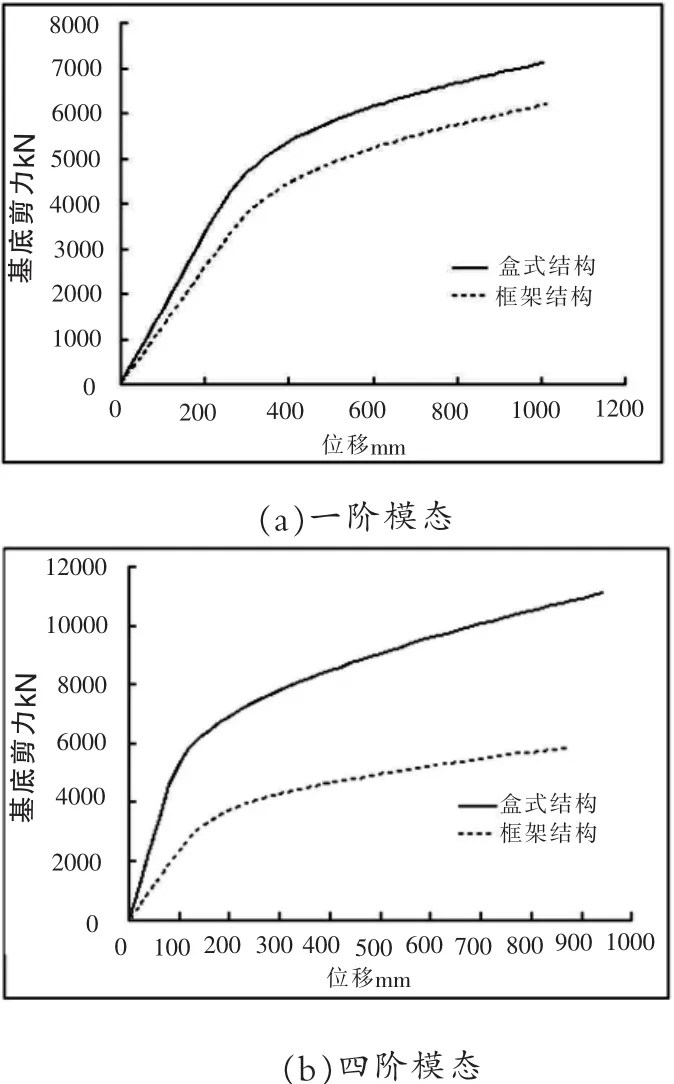
圖3基底剪力－最大層位移曲線

圖4 為兩種結構在各階振型下的側移剛度退化曲線。從圖4中可以看出：一階模態荷載模式下，彈性階段，盒式結構的側移剛度比框架結構大30%；彈塑性階段，盒式結構剛度退化快于框架結構；當最大層位移超過280mm以后，兩種結構體系的側移剛度基本相等。四階模態荷載模式下，彈性階段，盒式結構的側移剛度接近框架結構的2.5倍；彈塑性階段，盒式結構剛度退化快于框架結構，最大層位移達到180mm時，兩種結構的剛度基本相等；隨著位移的繼續增長，兩種結構體系的側移剛度差值逐漸變大，最終盒式結構的側移剛度保持為框架結構的2倍。

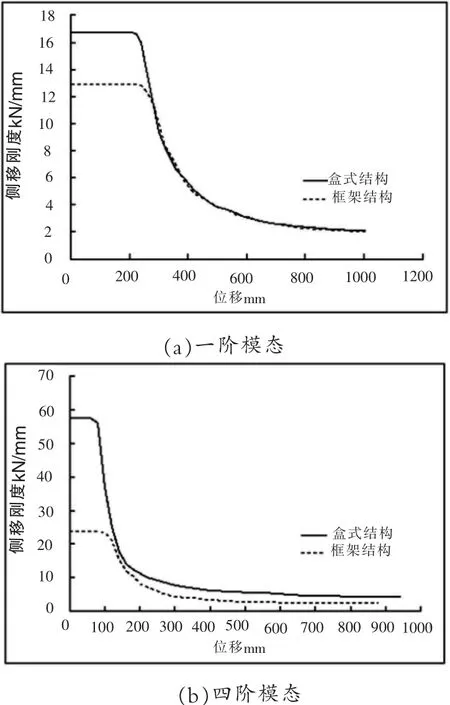
圖4 度退化曲線

3.2 求解目標位移

采用2.2節的方法，將基底剪力－位移曲線轉化為等效單自由度體系的能力譜曲線（Sd－Sa曲線），與彈塑性需求譜疊加在同一個坐標系中，得到各階振型荷載模式下的結構目標位移（表1）。

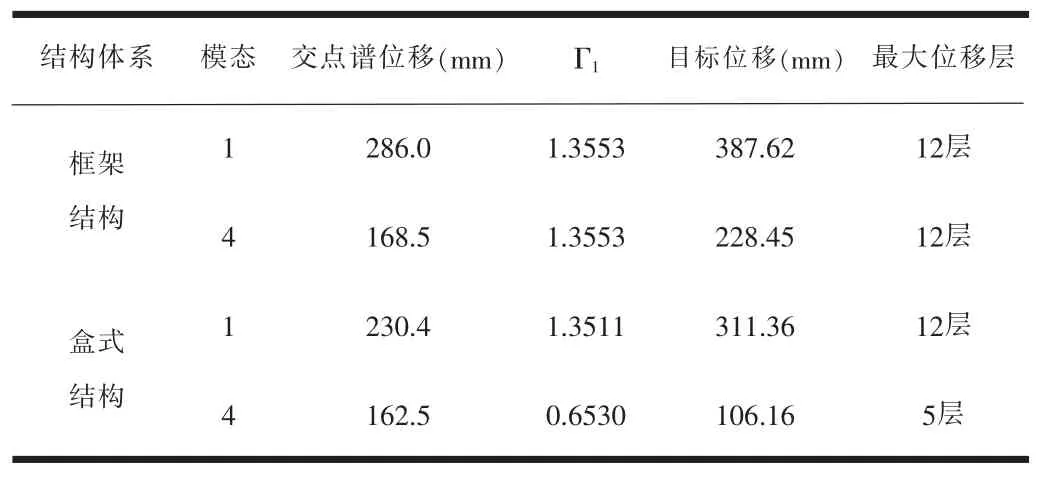
表1 結構目標位移

3.3 抗震性能評估

求出結構的層位移以及層間位移角分布。圖5給出結構各階模態下的層位移以及SRSS組合層位移，圖6給出了結構各階模態下的層間位移角以及SRSS組合層間位移角。

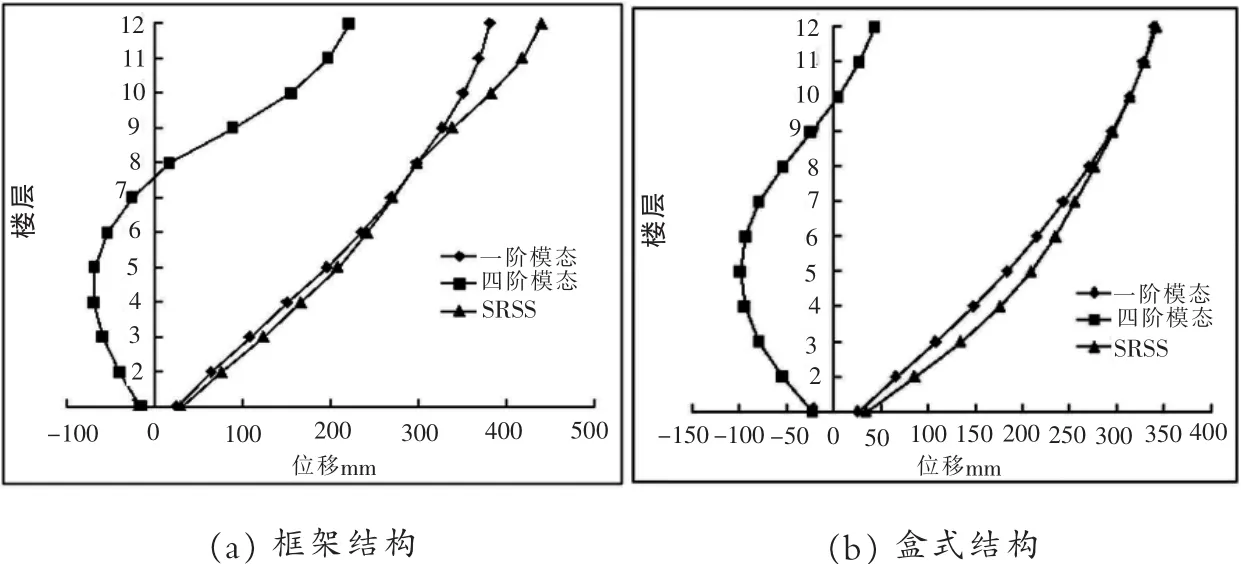
圖5 遇地震作用下樓層位移

從圖5、圖6中可以看出，兩種結構在罕遇地震作用下，兩種結構彈塑性層間位移角均小于規范限值1/50；高階振型對框架結構的8-12層的層位移及層間位移角影響較大，對1-7層影響較小；高階振型對盒式結構的1-8層的層位移及層間位移角影響較大，對9-12層影響較小。此外，盒式結構的層位移及層間位移角均小于框架結構；高階振型對盒式結構的影響小于框架結構。

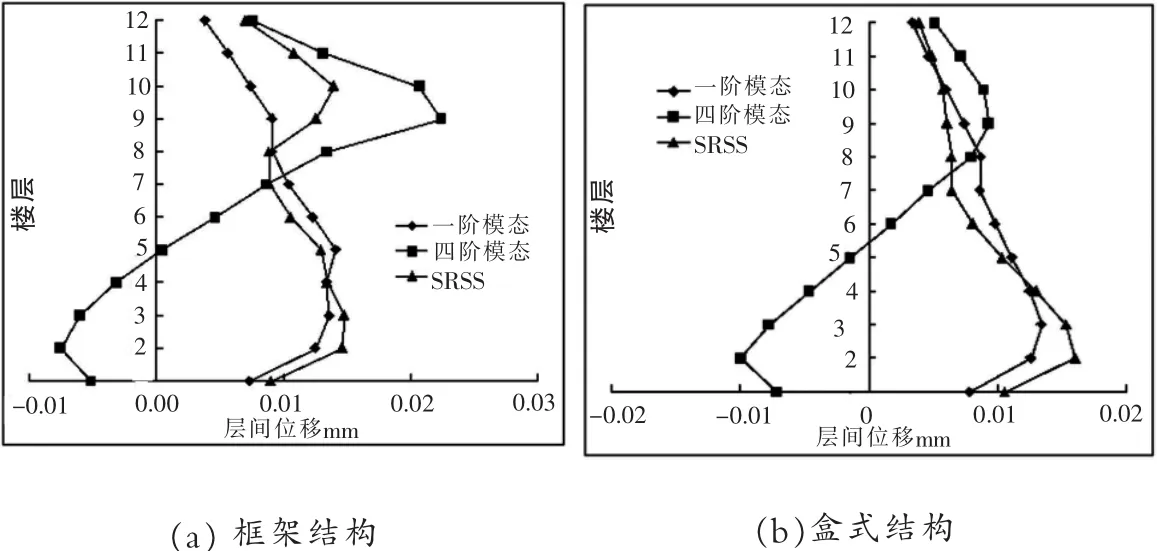
圖6 遇地震作用下層間位移角

4 結論

通過算例的抗震設計分析以及多模態靜力彈塑性分析，對比研究鋼網格盒式結構及框架結構的抗震性能，得出以下結論：

（1）設計地震作用下，鋼網格盒式結構周期比小于規范限值0.9，層間位移角小于規范限值1/250；罕遇地震作用下，層間位移角遠遠小于規范限值1/50，均滿足現行抗震設計規范要求。

（2）彈性階段，盒式結構側移剛度明顯高于框架結構。彈塑性階段，盒式結構的剛度退化快于框架結構，且其剛度仍一直大于框架結構。極限荷載下，兩者剛度較為接近。

（3）罕遇地震作用下，盒式結構層位移及層間位移角小于框架結構，高階振型對盒式結構的影響小于框架結構。

[1]孫濤，馬克儉，陳志華，等.石膏墻體鋼網格式框架結構基于改進能力譜法的抗震性能研究[J].空間結構，2011，17（4）：3-9.

[2]孫濤.現澆石膏外墻多高層鋼網格盒式節能住宅結構體系研究[D].天津：天津大學，2012.

[3]馬克儉，高國富，張華剛，等.空間網格式框架結構在多、高層大開間靈活劃分房間石膏節能建筑中的研究與應用綜述 [J].空間結構，2009，15（3）：62-84

[4]馬克儉，張華剛，周觀根，等.鋼結構石膏墻體大開間節能住宅建筑及現場分層分段制作方法[P].中國專利：CN101691784A，2010.

[5]孫濤，馬克儉，陳志華，等.多層石膏墻體鋼網格框架結構影響系數研究[J].建筑結構學報，2013，34（9）：66c72.

[6]Anil K.Chopra，Rakesh K.Goel.A modal pushover analysis procedure for estimating seismic demands for buildings[J].Earthquake Engineering and Structural Dynamics.2002，31:561-582.

[7]FederalEmergency ManagementAgency.NEHRP Recommended Provisions for Seismic Regulations for New Buildings and Other Structures （FEMA-369）[R].Washington DC：Building Seismic Safety Council，2000.

[8]Applied Technology Council.Seismic evaluation and retrofit of concrete buildings （ATC-40）[R].Rewood City，CA:Applied Technology Council，1996.

[9]T.Vidic，P.Fajfar and M.Fischinger.Consistent inelastic design spectra:strength and displacement[J].Earthquake Engineering and Structural Dynamics，1994，23（5）.

[10]李國豪.工程結構抗震動力學[M].上海：上海科學技術出版社，1980：75-80.

[11]GB50017-2003.鋼結構設計規范[S].北京：中國建筑工業出版社，2003：28-30.

[12]GB50011-2010.建筑抗震設計規范[S].北京：中國建筑工業出版社，2010：86-90.

[13]JGJ99-98.高層民用建筑鋼結構技術規程[S].北京：中國建筑工業出版社，2003：36-39.

[14]北京邁達斯技術有限公司.midas Gen工程應用指南[M].北京：中國建筑工業出版社，2012：15-18.