現代宜居城市排名評價方法
劉永坤 宋朝煬 鮑雅蘭
本文圍繞城市宜居性的評價問題進行研究, 構建評價指標體系,建立了基于神經網絡變量篩選模型、層次分析法評價模型、全局靈敏度分析法模型,評價各類因素對城市宜居性的影響,通過和求解出各個城市宜居性評價值。
一、問題的敘述
宜居性城市評價指標體系不同,宜居城市排名結果也會發生變化。一座宜居的城市不僅應具備物質豐足、生活便利等條件,而且應注重人們的切身感受。人們選擇留在某個城市,不單是為了生存,更是寄托了自己的夢想與希望。對很多人來說,衡量是否宜居或許就是八個字:衣、食、住、行、安、居、樂、業。
問題1:通過查閱資料,篩選評價宜居城市的主要指標,并闡述這些指標的合理性。根據所篩選的主要指標,建立評價宜居城市的數學模型。
問題2:構建的評價宜居城市的數學模型,對淮海經濟區內的8個城市(宿遷、連云港、宿州、商丘、濟寧、棗莊、徐州、淮北)進行合理性研究,給出宜居城市排名。
二、模型的建立與求解
1.問題1模型的建立與求解
(1)問題1模型的準備
①評價宜居城市指標的選取
為了建造一個合理而且實用性廣的評估宜居性城市模型,我們要對所有評估宜居性城市的指標做一個綜合性的概括。指標如圖1所示:
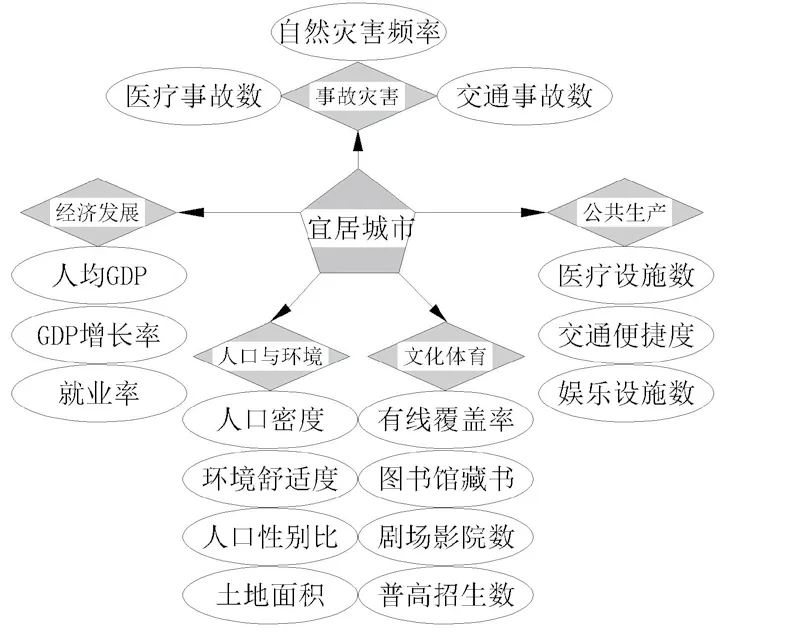
圖1 評價宜居城市的指標圖
②指標選取的合理性解釋
衡量是否宜居的八個字:衣食住行、安居樂業,表明醫療、娛樂等基礎設施也是其評價指標。經濟繁榮與就業又密不可分,人均等也就成為評價宜居性城市的重要指標之一。追求繁榮需要發揮城市聚集效應,追求舒適需要城市分散,為了城市有效經營必須遵守城市經濟學原理——分散與聚集人口密度,土地面積自然而然也成了評價指標。
(2)問題1模型的建立
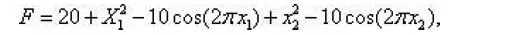

表1 兩兩因素對照表
為了確認權重的合理性,我們進行了一致性檢驗。
計算層次單排序并作一致性檢驗。對比較矩陣計算最大特征值及其對應的特征向量,利用一致性指標
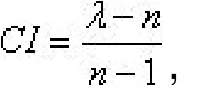
和一致性比率
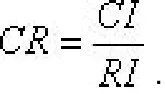
以醫療設施數量為例,首選我們查出給定的整個地區醫療設施的總數,計算出其對總人數的平均值。然后相應的根據每個城市的醫療設施總數為以及對應的人口總數,計算出其平均值,由此可用

作為第i個城市醫療設施對其宜居程度的影響。同樣的如果是成本型指標M,則可用
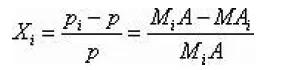
作為第i個城市的成本型指標對其宜居程度的影響。
2.問題2模型的建立與求解
通過查找影響城市宜居能力的指標,由于指標過多,計算時間耗費大,因此我們建立篩選模型對多個指標降維。
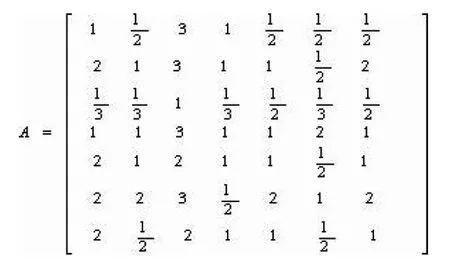
使用Matlab 程序進行計算各項權重,得
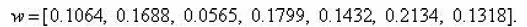
這里為了確認權重的合理性,我們進行了一致性檢驗。
和RI一致性指標
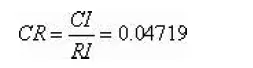
3.宜居評價值的求解
將各個指標的等級值乘上對應的權值,就可以得到各個城市宜居評價值數越大,就越說明該城市宜居程度越高.得到排名由高到低,徐州、濟寧、棗莊、連云港、宿州、商丘、淮北。
三、模型的改進與推廣
1.模型的改進
針對多層次分析法存在的缺陷,我們可對指標與研究對象的關系進行真實值代入,減少主觀因素的影響,對于不能得出最優結果的問題,我們可以盡可能地羅列滿足研究對象的可能方案,擴大范圍,一步步優化,進行篩選,最終得到最優秀的方案。
2.模型的推廣
我們所用的模型,可以運用到描述指標或者兩個知道大量數據的變量之間的關系上,得出的關系式比較精確,值得信賴;多層次分析法,可以很好地處理研究對象以及研究對象的影響因素之間的關系,使之能夠迅速地建立研究對象的研究值與變量之間的關系。
四、結語
本文建立的多指標體系,邏輯清晰地說明了影響研究對象的多層指標,為沒有數據的問題提供了定性分析的思路,多層次分析法,可以通過確定指標系數與現實數據,將研究對象量化,從而進行定量分析。

