基于極大似然估計的新息自適應濾波算法

張玉龍， 王 茁， 楊 巍

(1.海軍駐哈爾濱地區艦船配套軍事代表室，黑龍江 哈爾濱 150046；2.哈爾濱工業大學 電氣工程及自動化學院，黑龍江 哈爾濱 150001)

0 引 言

在常規卡爾曼濾波器中，根據先驗知識確定系統噪聲和量測噪聲的協方差陣后，噪聲協方差陣就一直作為常值參與濾波遞推過程。但在實際應用中，噪聲統計信息通常難以準確獲取，而且其統計特性受環境溫度、載體機動等外界因素影響會發生變化[1,2]。此時，常規卡爾曼濾波并不能根據外部量測數據來修正其噪聲參數，使得估計誤差不斷積累，導致濾波精度下降，甚至引起濾波發散[3,4]。

近年來，為了解決常規卡爾曼濾波在噪聲統計信息未知或者時變情況下存在的問題，相繼提出了各種自適應濾波算法，主要包括基于極大后驗估計的Sage-Husa自適應濾波[5]、基于極大似然估計(maximum likelihood estimation,MLE)的自適應濾波[6]以及各種漸消自適應濾波[7]等。其中，Sage-Husa自適應濾波能夠通過實時估計噪聲的統計特性提高濾波器的估計精度，但噪聲統計信息估值器常處于臨界穩定狀態[8],容易導致濾波器發散；漸消自適應濾波通過增大濾波一步預測均方誤差陣提高新近量測數據權重，但標量漸消因子的計算過程較為繁瑣[9]，而且對各濾波通道具有相同調節能力，不利于改善濾波器的穩定性和精度；常規的MLE自適應濾波雖然能夠在線估計與修正噪聲統計特性的二階矩，但是需要依賴于準確的新息協方差估計值，而目前利用開窗法得到的新息協方差估值器并不能突出滑動窗口內新近協方差序列的作用[10]，限制了進一步提高其估計精度。

為了提高濾波器在噪聲統計信息未知或者時變情況下的估計精度，首先本文在得到基于極大似然估計的新息協方差估值器后，提出了一種基于限定記憶指數衰減加權的改進算法, 利用新息協方差的指數加權值代替其算數平均值，提高了新息估計的精度。對捷聯慣性導航系統/全球定位系統(strapdown inertial navigation system/global positioning system,SINS/GPS)組合導航系統的仿真表明:與基于MLE自適應濾波相比，本文算法在噪聲統計信息未知或者時變情況下具有更強的魯棒性，而且濾波精度得到了顯著提高。

1 基于MLE的新息協方差估值器

考查動態離散系統，其狀態方程和量測方程分別滿足

Xk=Φk,k-1Xk-1+Γk-1Wk-1

(1)

Zk=HkXk+Vk

(2)

式中Xk為n維狀態序列；Φk,k-1為n×n階一步轉移矩陣;Γk為n×p階系統噪聲系數陣;Zk為m維量測序列;Hk為m×n階量測陣;Wk為p維系統噪聲序列;Vk為m維量測噪聲序列。Wk和Vk是不相關的高斯白噪聲，噪聲統計特性滿足

E[W(k)]=0,Cov[W(k),W(j)]=Q(k)δkj

E[V(k)]=0,Cov[V(k),V(j)]=R(k)δkj

Cov[W(k),V(j)]=0

式中δkj為Kronecker-δ函數；假定協方差陣Qk為m×n階非負定陣；Rk為m×m階正定陣。

設狀態一步預測值為

(3)

狀態估計值為

(4)

式中

(5)

εk=Zk-Hkk/k-1

(6)

式中Kk為濾波增益矩陣；Pk/k-1為一步預測均方誤差;εk為新息序列，且其協方差理論值滿足

(7)

(8)

將式(8)代入式(5)中，即可得到簡化的濾波增益矩陣

(9)

在新息自適應濾波器中由式(9)代替式(5)，即利用新息協方差的實際估計值代替其理論估計值，可以加快濾波器的收斂速度，同時修正由于噪聲統計特性未知或者時變而引入的估計誤差，改善濾波精度。下面將利用極大似然估計證明式(8)的結論。

極大似然估計是從系統量測量出現概率最大的角度進行估計，在k時刻ζ條件下Z的條件概率密度函數滿足

(10)

式中ζ為系統參數；m為量測陣維數；|·|為矩陣行列式。

對式(10)取對數

(11)

對式(11)進行累加運算，求取和式的極大值可轉化為

(12)

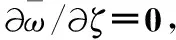
(13)

最終得到基于極大似然估計的新息協方差估值器，其表達式如式(8)所示。

通過式(8)發現，新息協方差在k時刻的估計值k是對先前所有時刻新息協方差的算數平均，即先前所有數據具有相同的利用權重；但對于動態系統而言，需要更加強調新近新息序列在濾波器中的作用，為此文獻[11]采用了開窗法求取新息協方差的估計值，即對限定長度的滑動窗口內的新息協方差進行算數平均，其表達式為

(14)

式中N為滑動窗口長度。

由式(14)可以看出，利用開窗法求取新息協方差估計值實質上僅截取了新近一段長度為N的新息協方差序列，并對其進行算數平均，但仍未提高滑動窗口內新近數據的利用權重。

為此，本文提出了一種基于限定記憶指數衰減加權的新息協方差估值器,通過對滑窗內數據進行指數衰減加權，突出新近數據的作用。

2 基于限定記憶指數加權的新息協方差值器

考察限定記憶長度為N的新息協方差序列，為提高該序列中新近數據的利用權重，將當前時刻新息協方差權重看作基準，并依次對滑動窗口內的先前協方差進行指數衰減加權，最終得到新息協方差在當前時刻的估計值。

當k>N時，選取加權系數{αi}，在k時刻使之滿足

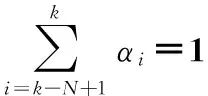
于是有

(15)

(16)

對于k時刻的新息協方差估計值k滿足

(17)

將αi展開并代入式(17)，整理得到

(18)

式(18)即基于限定記憶指數加權的新息協方差估值器在k時刻的表達式。

同理，對于k-1時刻的新息協方差估計值k-1成立

(19)

由式(18)、式(19)可以得到限定記憶指數加權的新息協方差估值器的遞推形式

(20)

另外，當k≤N時，新息協方差估計值則取其極大似然估計值，其表達式如式(8)所示。

將式(20)代入式(9)，用基于限定記憶指數加權的新息協方差估計值代替滑窗內新息協方差序列的算數平均值，不僅可以增加新近量測數據在濾波器中的利用權重，同時還可以提高新息協方差估計值的精度。

3 仿真結果與分析

為了驗證本文提出的基于極大似然估計的新息自適應濾波算法在噪聲統計信息未知和時變情況下的濾波性能，設置在SINS/GPS組合導航系統中進行仿真實驗，并針對兩種情況，進行了2組仿真實驗。

實驗選取SINS為主導航系統，速度誤差、位置誤差以及失準角為狀態向量，并根據SINS誤差方程建立濾波器的狀態方程，GPS作為輔助導航系統提供量測信息，SINS/GPS組合導航系統模型具體參數參見文獻[12]，利用輸出反饋修正SINS輸出的導航參數。分別采用文獻[10]基于MLE自適應濾波算法和本文提出的基于極大似然估計的新息自適應濾波算法對載體的速度及位置誤差等參數進行估計，濾波算法性能可以通過SINS/GPS組合導航系統速度及位置的估計誤差衡量。其中，本文算法的濾波參數中衰減因子取b=0.7，滑動窗口長度取N=15；MLE自適應濾波的滑動窗口長度取M=20。仿真條件設置如下：載體運動速度為(3m/s,4m/s,0m/s),姿態角為(1°,1°,5°),初始經緯度為(126.67°,45.77°);仿真時間為500s,采樣周期為0.1s；濾波器初始參數設置如下

P(0)=diag{(20m/Re)2,(20m/Re)2,(0.1m/s)2,

(0.1m/s)2,(0.1°)2,(0.1°)2,(0.1°)2}

Q(0)=diag{(100μg)2,(100μg)2,(0.01°/h)2,

(0.01°/h)2,(0.01°/h)2}

R(0)=diag{(0.1m/s)2,(0.1m/s)2}

式中Re為地球半徑，Re=6378393m。

3.1 量測噪聲協方差未知情況下仿真

由于缺乏相關的先驗信息等因素導致無法得到實際量測噪聲的統計特性；針對量測噪聲協方差未知的情況，實驗選取濾波器中量測噪聲協方差初值為R=0.01R(0)，濾波結果如圖1所示。

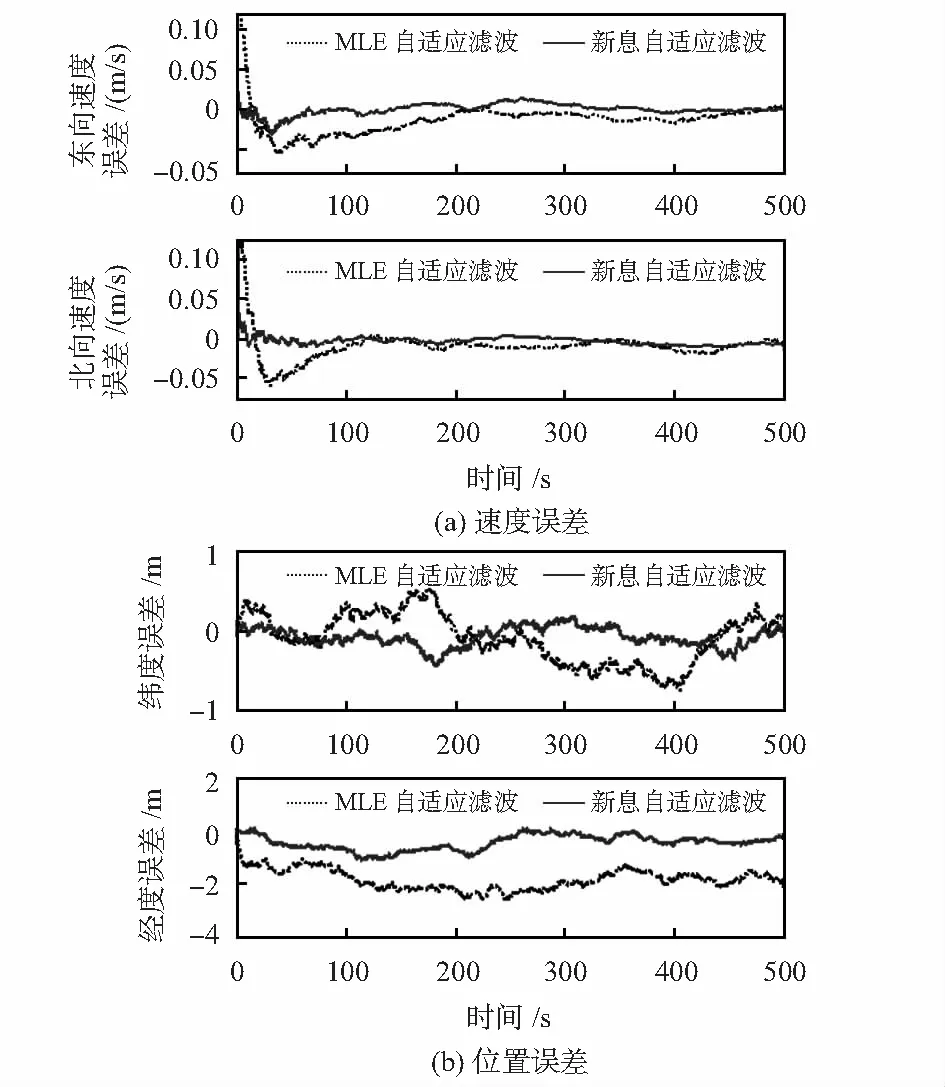
圖1 噪聲統計信息未知濾波性能

可以看出:在量測噪聲統計信息未知條件下，MLE自適應濾波算法中速度估計誤差在前200s出現較大的波動，這是由于濾波器中量測噪聲協方差初值設置不準確，雖然經過一段時間的自適應調節后逐漸達到收斂，但受其影響，位置估計誤差不斷積累；而本文的新息自適應濾波算法能夠利用新息協方差的估計值直接修正濾波增益矩陣，經過較短時間的調節就能克服由量測噪聲不準確引起的干擾，整個過程變化較為平穩，位置估計誤差也較小。

3.2 量測噪聲協方差時變情況下仿真

受環境溫度、載體機動等外界因素影響導致量測噪聲協方差不再保持常值，而是隨時間變化；為此，仿真實驗設置了3組不同強度的量測噪聲：幅值在50～100s變為R=40R(0)，在300～320s變為R=20R(0)，其余時間段幅值R=R(0)，濾波結果如圖2所示。

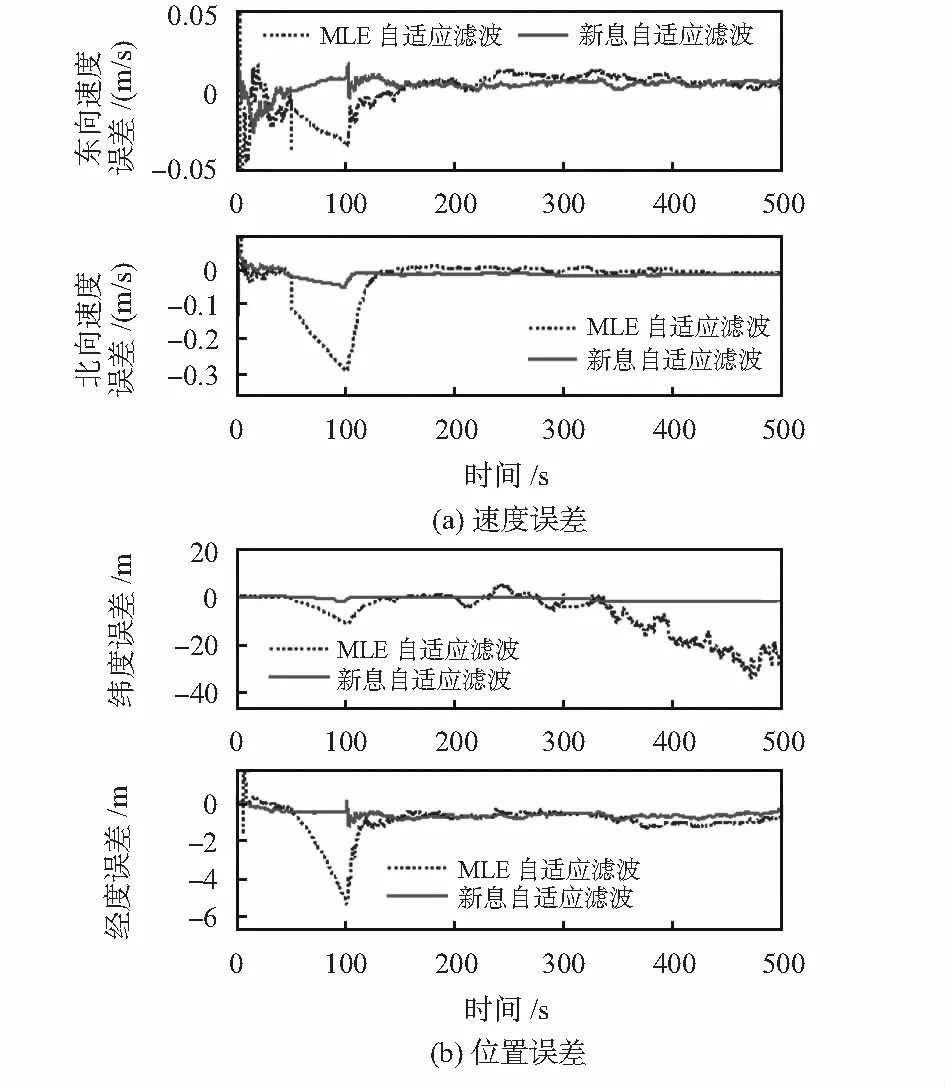
圖2 噪聲統計信息時變濾波性能

可以看出:在量測噪聲時變情況下， MLE自適應濾波的估計誤差波動幅度較大：在50～150s處出現幅值較大的鋸齒狀速度估計誤差，而且位置誤差也出現較大幅值的波動，緯度誤差在300s后顯著增大。對于本文的新息自適應濾波，雖然在量測噪聲幅值變化時間段出現了一定的擾動，但幅值較小，而且經過很短時間的調節后便收斂于穩態，這是因為其基于限定記憶指數加權的新息協方差估值器能夠充分利用滑動窗口內新近新息協方差序列的作用，根據新近的量測信息及時地修正濾波增益矩陣，從而克服了由噪聲時變帶來的影響。

4 結 論

針對噪聲統計信息未知或者時變情況下，常規卡爾曼濾波估計精度下降甚至發散的問題，提出了一種基于極大似然估計的新息自適應濾波算法。算法通過引入限定記憶指數衰減加權法來修正由基于極大似然估計得到的新息協方差估值器，利用新息協方差的指數加權值代替其算數平均值，增加滑動窗口內新近數據的權重，提高新息協方差估計值的準確性。對SINS/GPS組合導航系統的仿真實驗驗證了本文算法具有更強的魯棒性和更高的濾波精度。

[1] Kwok C,Dev K,Seebauer E G,et al.Maximum a posteriori estimation of activation energies that control silicon self-diffu-sion[J].Automatica,2008,44(9):2241-2247.

[2] Karasalo M,Hu X.An optimization approach to adaptive Kalman filtering[J].Automatica,2011,47(8):1785-1793.

[3] Xiong K,Liu L D,Zhang H Y.Modified unscented Kalman filtering and its application in autonomous satellite navigation[J].Aerospace Science and Technology,2009,13(4):238-246.

[4] 王小旭，趙 琳.自適應融合濾波算法及其在INS/GPS 組合導航中的應用[J].宇航學報,2010,31(11):2503-2511.

[5] Sage A P,Husa G W.Algorithms for sequential adaptive estimation of prior statistics[C]∥Proc of8th IEEE Symposium on Adaptive Processes,1969:61.

[6] 岳曉奎,袁建平.一種基于極大似然準則的自適應卡爾曼濾波算法[J].西北工業大學學報,2005,23(4):469-474.

[7] Yang Y,Gao W.An optimal adaptive Kalman filter[J].Journal of Geodesy,2006,80(4):177-183.

[8] 張常云.自適應濾波方法研究[J].航空學報,1998,19(7):96-99.

[9] 徐定杰，賀 瑞，沈 峰,等.基于新息協方差的自適應漸消卡爾曼濾波器[J]. 系統工程與電子技術,2011,33(12):

2696-2699.

[10] Mohamed A H,Schwarz K P.Adaptive Kalman filtering for INS/GPS[J].Journal of Geodesy,1999,73(4):193-203.

[11] 卞鴻巍,金志華,王俊璞,等.組合導航系統新息自適應卡爾曼濾波算法[J].上海交通大學學報,2006,40(6):1000-1003.

[12] Gao W,Li J C.Adaptive Kalman filtering for the integrated SINS/DVL system[J].Journal of Computational Information Systems,2013,9(16):6443-6450.