地下綜合管廊邊界條件對地震動力響應影響數值分析

施有志,柴建峰,林樹枝,李秀芳

1.廈門理工學院土木工程與建筑學院,福建 廈門 361024 2.上海交通大學船舶海洋與建筑工程學院,上海 200240 3.國網新源控股有限公司技術中心,北京 100161 4.廈門市建設局,福建 廈門 361003

0 引言

綜合管廊是建于城市地下用于容納兩類及以上城市工程管線的構筑物及附屬設施[1]。地下綜合管廊相比直埋管線具有很多優點，是城市現代化發展的必然趨勢，目前很多城市正在開展綜合管廊的建設或規劃。既有的震害記錄表明，地下結構在地震過程中會遭到嚴重破壞，應引起地震工作者的重視[2]。由于室內試驗費用高、周期長，數值分析成為地下結構動力響應分析的重要手段。對于半無限地基中地下結構的動力響應分析，目前廣泛采用的數值模擬技術是從半無限域中切取有限尺寸的近場計算區，此時需要在計算域邊界上引入虛擬的人工邊界，以消除反射、模擬遠場介質的輻射阻尼效應[3-7]。合理設置人工邊界是實現對真實波動的直接模擬、解決土-結構相互作用問題的關鍵。人工邊界可以分為靜力人工邊界和動力人工邊界兩大類。靜力人工邊界是基于靜力學基本理論建立的，但已有研究表明，以固定邊界為代表的靜力人工邊界與波動在半無限介質中的傳播規律不符[8-9]。目前廣泛應用的動力人工邊界主要是基于單側波動概念的局部人工邊界，比如黏性邊界[10-11]、黏彈性邊界[12-17]、透射邊界[18]等。

因概念清楚、簡單方便，黏性邊界應用最為廣泛，但其僅考慮了對散射波能量的吸收。從物理概念上理解，施加黏性邊界后的力學模型為懸浮在空中的脫離體，其在低頻力作用下可能發生整體漂移；此外，黏性邊界是基于一維波動理論提出的，簡單地將其推廣到多維情況將導致相當誤差[19]。相比而言，黏彈性邊界可以約束動力問題中的零頻分量，能夠模擬人工邊界外半無限介質的彈性恢復性能，具有良好的穩定性和較高的精度。不過，黏彈性邊界建模時，需逐點計算并施加彈簧及阻尼器，前處理工作量大；實際應用中，為了便于施加黏彈性邊界，通常采用一些近似處理，這會對計算精度造成一定程度的影響[20]。無論是黏性邊界還是黏彈性邊界都屬于吸收邊界，只考慮了對外行波的吸收效果，未考慮地震動輸入問題。地震動輸入一般基于波場分離法，即在底邊界輸入入射波場、在側邊界輸入自由波場來實現，因此在均勻巖土體中，側邊界的自由波場采用一種延時的方法得到。但是在實際的數值計算中，施加側邊吸收邊界和輸入自由場地震動工作量浩大，前處理繁雜；而且在實際巖土工程中，巖土體往往具有不均勻性和非線性的力學特征，通常會出現水平分層現象，每一層土體具有不同的動力學特性。此時很難通過簡單的延時方法得到自由場地的地震反應，而要利用波的頻域分析、反射透射理論、波幅系數轉換等更復雜的波動理論來計算波動在土層間的傳播與疊加。

要想解決此問題，可以采用SHAKE91和EERA等一維土層動力反應分析軟件計算水平成層場地的地震反應或者在有限元(有限差分)軟件中同步計算自由場地地震反應，從而獲得側邊界地震動輸入所需要的自由波場，這樣也就實現了自由場運動和計算模型側邊界的完美耦聯。此理論也就是我們所熟悉的自由場邊界的思想基礎，它最早由Seed等[21]提出，目前已在PLAXIS、FLAC等數值模擬軟件中得到廣泛應用，但這些人工邊界本身固有的優缺點及其局限性仍然存在。以PLAXIS中內置的黏性邊界為例，其松弛系數C1和C2需要建立一系列模型進行試算確定，才可獲得較好的動力響應效果；自由場邊界具有較好的場地動力響應，但其適用性也需進行驗證和深入探討。

為研究綜合管廊動力邊界條件對地震動力響應的影響，本文以廈門地區的代表性土層為例，分別研究了固定邊界、黏性邊界和自由場3種人工邊界在Rayleigh波和地震底部剪切波作用下的場地響應，并根據加速度時程和擬絕對加速度反應譜(PSA)評價了3種邊界的有效性；進而提出綜合管廊地震動力分析的優化動力邊界組合。

1 邊界條件在數值分析軟件中的實現

1.1 黏性邊界

黏性邊界的基本思想是在人工邊界上設置阻尼器，以吸收振動過程中的散射波能量。PLAXIS軟件提供了基于該方法建立的黏性邊界條件。地震分析中，如果在模型底部設置黏性邊界，則地震輸入應為荷載時程。

以邊界上x方向的某一阻尼器為例，其吸收的法向和切向應力分量分別為

(1)

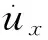
松弛系數C1和C2用于改善黏性邊界的波動吸收效果：C1調整沿邊界法向的能量耗散；C2調整沿邊界切向的能量耗散。若邊界上只受到法向波動，則無需考慮松弛，此時C1=C2=1。一般情況下，波動方向并非僅垂直于邊界，而是沿任意方向，此時應調整C2的值以改善吸收效果。

1.2 自由場邊界

黏性邊界與黏彈性邊界對爆破等內源問題比較有效，但因其均屬于吸收邊界，主要考慮對外行波的吸收效果，而沒有考慮地震動的輸入問題，因此尚不能很好地解決地震等外源問題。通常，地震波考慮為底邊界垂直入射，此時兩側邊界內行波場為自由波場[22]。自由場邊界通過“強制”自由場運動，同時保證工程計算區域產生的外行波被適當地吸收，以模擬無限域邊界條件。在有限元軟件中，通過在模型四周生成與其邊界節點對應的自由場網格來實現自由場邊界條件，主網格的側邊界與自由場網格通過阻尼器(黏性邊界)進行耦合，以吸收有結構存在時入射地震波發生的散射；在求解過程中，主網格進行計算時自由場網格也進行同步運算，自由場網格的不平衡力會施加到主網格的側邊界上以滿足側邊界上的位移和應力條件。自由場提供的條件與無限場地完全相同。自由場邊接觸面上所施加的沿x、y、z方向的不平衡力Fx、Fy、Fz表達式為

(2)

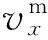
PLAXIS中自由場邊界的實現與上述方法類似。自由場邊界由荷載時程和黏性邊界組成，荷載時程由自由場運動產生。荷載時程和黏性邊界結合而成的自由場邊界，能夠同時實現模型邊界上地震動輸入和對散射波的吸收。

2 動力有限元數值模型

2.1 工程概況

廈門湖邊水庫綜合管廊長約5.2 km，斷面形式主要有矩形單倉(3.0 m×2.8 m)、雙倉(5.6 m×2.8 m)(圖 1)和三倉(8.6 m×2.8 m)，以及單倉圓形(內徑3.4 m)，管廊埋深3.0～5.0 m，管廊結構為預制形式；納入的管線主要為110、220 kV高壓電纜，10 kV電力、通訊電纜，給水、有線電視、交通信號及預留管線。

圖1 雙倉綜合管廊Fig.1 Double chamber utility tunnel

基坑開挖揭露土層情況：填土(已建道路為填筑土)，最大厚度2.4 m；以下為粉質黏土、殘積土、全風化花崗巖、強風化花崗巖及中風化花崗巖。填土透水性中等，總體水量不大；粉質黏土、殘積土及散體狀強風化花崗巖屬弱透水弱含水層，水量較小。場地局部為空地，周邊房屋大部分為3～4層的磚混結構民房及廠房，場地內及附近無不良地質作用和地質災害。綜合管廊采用明挖基坑埋設預制管廊結構，基坑寬度為9～12 m，開挖深度一般為5.5 m，局部地段基坑開挖深度最大為14.5 m。圖 2為單倉圓形現場吊裝圖。

圖2 預制綜合管廊現場吊裝Fig.2 Field hoisting of prefabricated utility tunnel

2.2 數值模型

為了對比二維模型與三維模型對計算結果的差異，分別建立二維數值模型和三維數值模型。二維數值模型水平方向長100 m，地表以下土體深度取30 m，如圖3a所示。三維模型尺寸為100 m×100 m×30 m，如圖 3b所示。靜力邊界均為模型側邊界法向約束，底部固定約束。

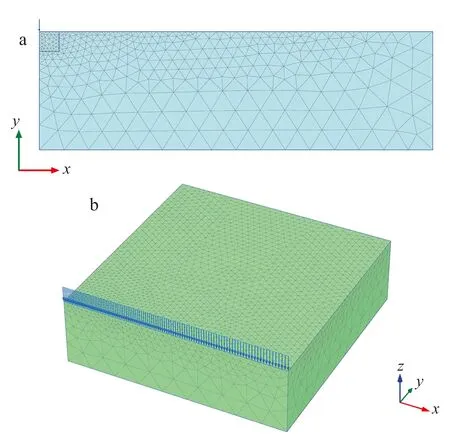
a.二維；b.三維。圖3 動力邊界研究數值模型Fig.3 Numerical models for studying dynamic boundary conditions

計算過程中，在模型中設置監測點(圖 4)。圖 4a中，A，B，C，D，E的坐標分別為(40,0)，(50,0)，(60,0)，(70,0)， (80,0)；圖 4b中，A，B，C，D，E的坐標分別為(50,50,0)，(0,50,0)，(100,50,0)，(50,50,-15)，(50,50,-30)。

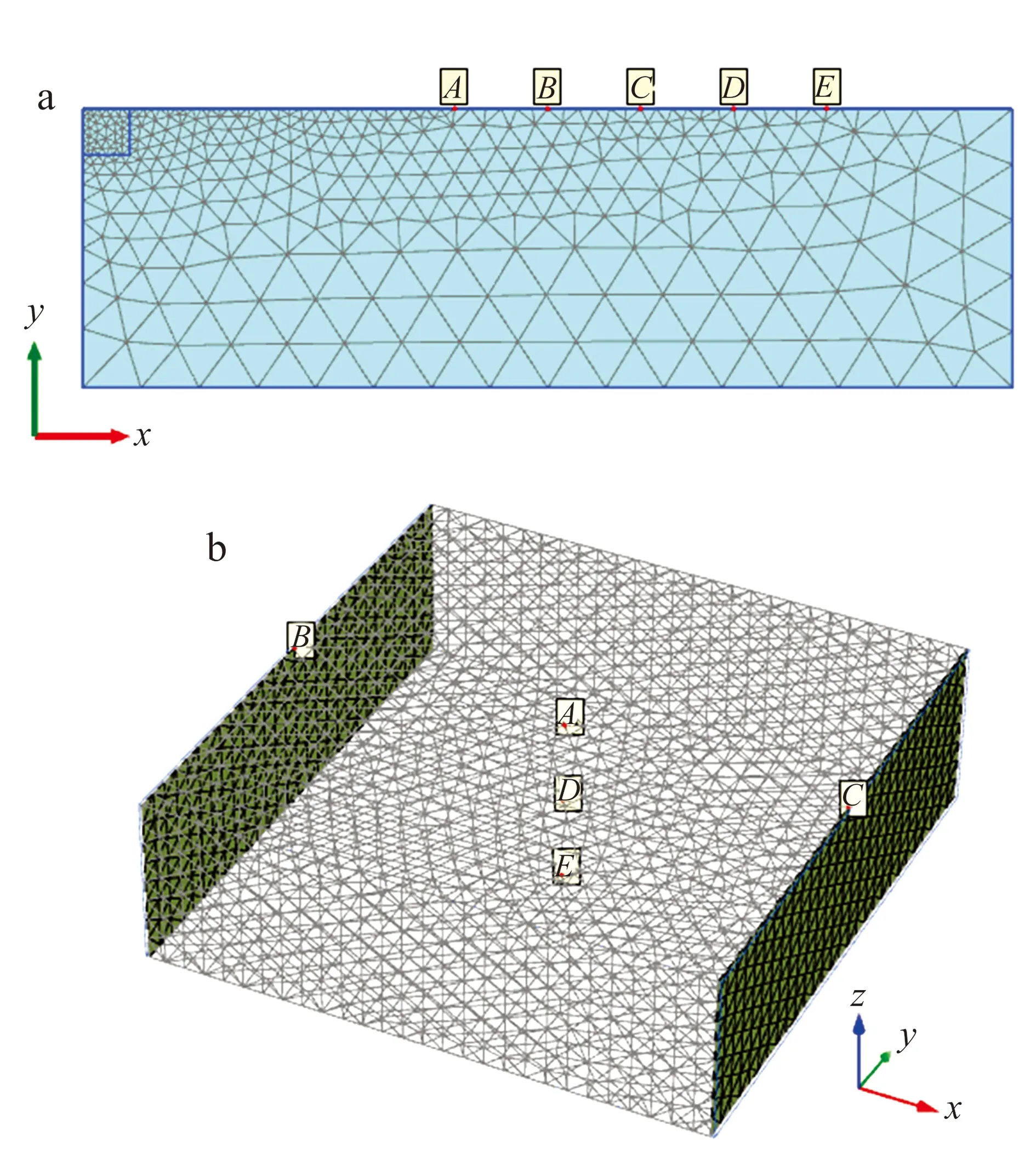
a.二維；b.三維。圖4 不同模型監測點布置Fig.4 Layout of monitoring sites in different numerical models

2.3 計算參數

廈門地鐵深基坑開挖深度15.0～25.0 m揭示的土層主要為人工填土、粉質黏土、淤泥質土和殘積砂質黏性土。表層人工填土厚度一般為0.5～3.0 m；粉質黏土和淤泥質土在大部分地區普遍連續分布，埋深較淺；殘積土埋深和厚度變化大，埋深為8.0～20.0 m，平均厚度可達10.0～16.0 m。城市綜合管廊通常埋深較淺，一般情況下會處于粉質黏土層中，因此，主要取粉質黏土層作為綜合管廊的埋置地層。

土體本構模型采用小應變硬化模型 (hardening soil model with smallstrain stiffness，HSS)。以廈門地區為例，結合地勘報告及參數優化結果，確定地基土基本物理力學參數見表 1。

2.4 動力荷載作用

福建省南部是東南沿海地震帶活動相對頻繁和強烈的地區，自1445年以來共發震級Ms≥5的強震8次。廈門市地處我國東南沿海地震帶，遭受的震害主要是區外強震的波及。根據剪切波速測試結果，依國標《鐵路工程抗震設計規范》(GB50111-2006)[23]有關標準劃分，場地土類型為軟弱土。另據鉆探揭露和波速測試結果，場地覆蓋層厚度小于50 m，依《建筑抗震設計規范》(GB50011-2001)[24]有關標準劃分，擬建場地類別綜合按Ⅱ類考慮。

表1廈門地區典型土層HSS模型參數

Table1HSSmodelparametersoftypicalXiamensoillayers

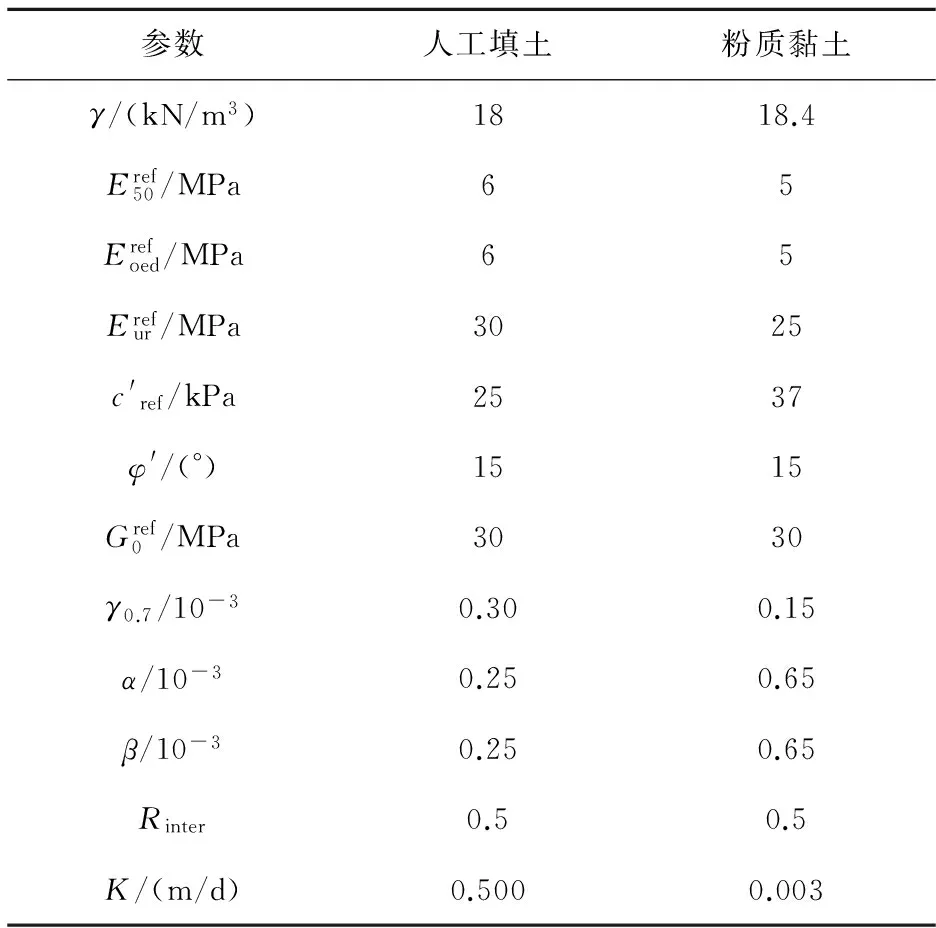
參數人工填土粉質黏土γ/(kN/m3)1818.4Eref50/MPa65Erefoed/MPa65Erefur/MPa3025c'ref/kPa2537φ'/(°)1515Gref0/MPa3030γ0.7/10-30.300.15α/10-30.250.65β/10-30.250.65Rinter0.50.5K/(m/d)0.5000.003

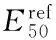
為了模擬動力荷載產生的Rayleigh波，借鑒Lamb[25]問題施加荷載的方式，在邊界上施加一個脈沖激勵荷載。動力荷載采用隨時間按三角形變化的荷載來模擬，自0.05 s之后開始施加荷載，荷載持續時間取0.025 s，荷載振幅取50 kN。關于該方法激勵Rayleigh波的可行性筆者已在文獻[26]中論證。

由于本文的重點在于研究邊界條件對地震動力響應的影響，而非實際綜合管廊的動力響應分析，因此采用PLAXIS程序的美國Upland波作為底部動力時程，峰值加速度0.2g(g為重力加深度)，如圖 5所示。它的強度適中，與Rayleigh波的強度也較為匹配。經過試算，在該地震波作用下，同時激活的Rayleigh波能夠產生顯著的影響。

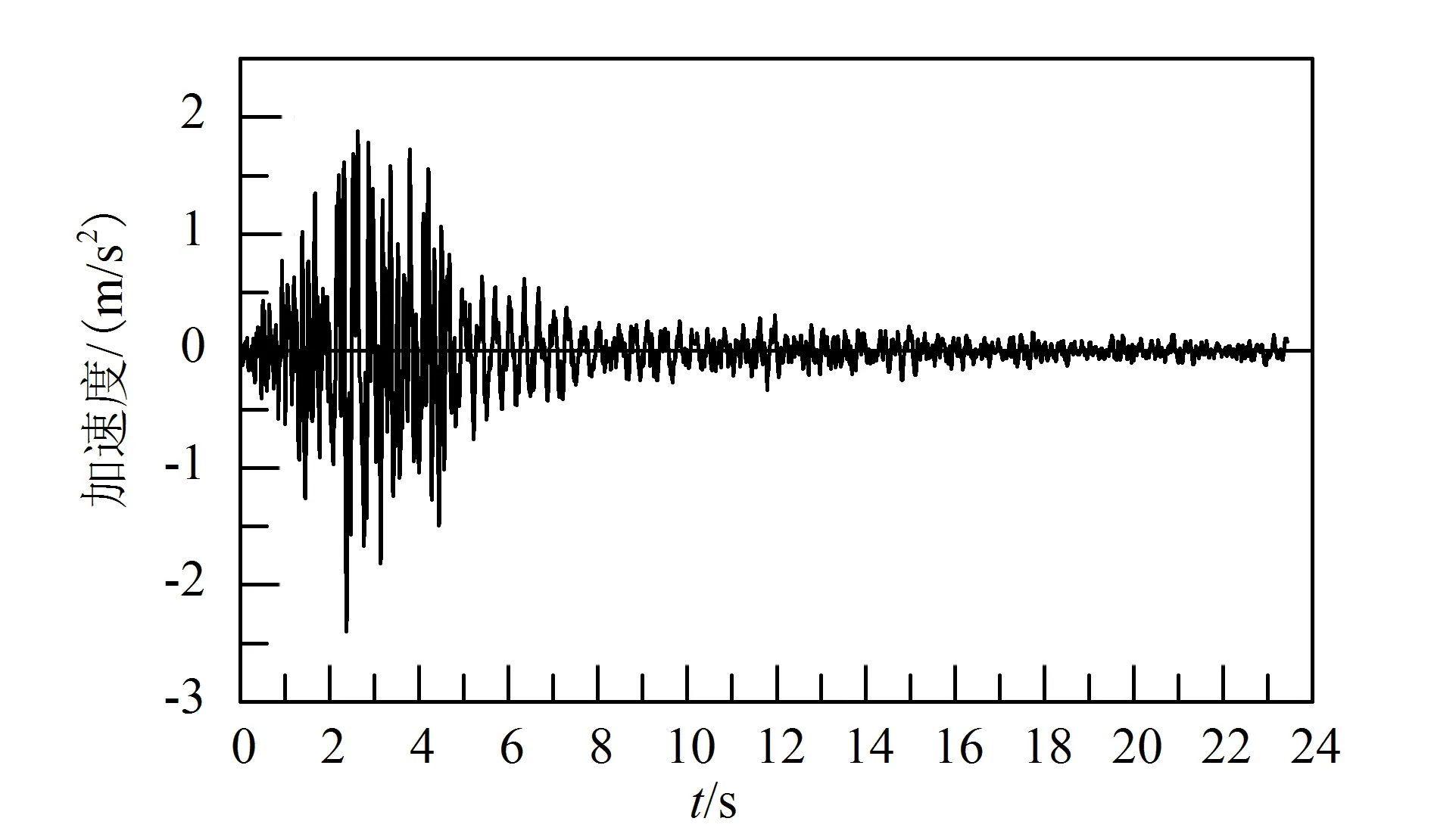
t為時間。圖5 美國加利福尼亞Upland地震波加速度時程曲線(NE155°方向)Fig.5 Acceleration time history curve for seismic waves in Upland, California (in NE155° direction)

3 Rayleigh波作用下動力邊界影響分析

3.1 計算方案

Rayleigh波作用下不同動力邊界條件對場地動力響應的影響研究計算方案見表2。

3.2 計算結果

以二維應變模型中心監測點B(50，0)為例，輸出其在Rayleigh波作用下隨動力作用時間的動力響應曲線，如圖 6所示。

從圖 6a可以看出：對于Rayleigh波采用兩側自由場邊界(方案3)時，uy-t曲線震蕩非常大，但能量經過傳播后，耗散較慢；采用兩側黏性邊界(方案2)時，過大吸收荷載激勵的耗散導致傳遞到監測點位置的波能量很小，uy仍在0左右小幅波動；采用兩側固定邊界(方案1)和激勵側固定邊界另一側黏性邊界(方案4)時，可以看到波的初次到達相差不大(約0.1 s)；而后的震蕩過程中，方案4波動較小，具有更好的收斂性，能夠在Rayleigh波的動力分析中獲得更好的場地響應。因此，將方案4的邊界稱為優化邊界條件。

表2 Rayleigh波作用下動力邊界影響研究計算方案

注：方案1—7為二維模型，模型尺寸為長×寬；方案8為三維模型，模型尺寸為長×寬×高。MC為摩爾庫倫模型。

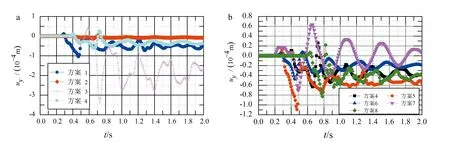
a.方案1—4的豎向位移-動力時間曲線；b. 方案4—8的豎向位移-動力時間曲線。t為時間。圖6 Rayleigh波作用下不同方案時平面模型監測點B(50,0)動力響應曲線Fig.6 Dynamic response curves for the monitoring site B(50,0) in a planar model with different calculation schemes under the effects of Rayleigh waves

在采用優化邊界條件下，分別考慮松弛系數變化(方案5)、Rayleigh阻尼變化(方案6)、土體為摩爾庫倫(MC)本構模型(方案7)以及三維模型(方案8)的情況，與方案4得到的監測點B(50，0)豎向位移時程曲線共同繪于圖 6b。

通過圖 6b可以看出：動力邊界松弛系數(方案5)變化對場地動力響應影響較小；增大地基的材料阻尼系數β(方案6)使得其動力響應振幅減小且衰減速度更快；采用MC材料本構模型(方案7)時由于沒有滯回阻尼導致振蕩幅度過大、衰減緩慢；三維(方案8)與二維模型結果體現的場地動力響應規律一致。

綜上所述，在Rayleigh波作用下，采用本文所提的優化邊界，不會使過大的吸收荷載激勵導致能量衰減過快，能考慮到動力作用的震蕩效應，又能較好地收斂，具有較好的動力響應結果。

4 Rayleigh波+底部地震波激勵共同作用下動力邊界影響分析

4.1 計算方案

Rayleigh波和地震波共同作用下不同動力邊界條件對場地動力響應的影響研究計算方案見表 3。其中底部地震波采用美國加利福尼亞Upland地震波加速度時程(圖5)。

4.2 計算結果

場地水平加速度ax(以g表示)的云圖如圖 7所示。

從圖 7可以看出：采用黏性邊界(圖 7a)時，場地水平加速度響應不成層，此外，模型兩側邊界效應明顯；采用自由場邊界(圖7b)時，場地水平加速度響應表現出較規律的成層性分布特征，且模型兩側邊界無明顯的過度吸收或者能量反射現象。

以位于模型表面中心的監測點B(50,0)為例，將兩側黏性邊界(方案9)、兩側自由場邊界(方案10)、模型長度增大(方案11)和減小(方案12)4種情況下的點B水平位移時程曲線、加速度頻譜和PSA峰值共同繪于圖 8。

從圖 8可知：模型兩側采用自由場邊界時，無論模型水平尺寸取與黏性邊界模型尺寸相同，還是比之更大或更小的模型尺寸時，自由場邊界下的點B水平位移都比黏性邊界下的點B水平位移偏大一些(圖8a)，進一步表明黏性邊界限制了模型內部土體的水平位移；黏性邊界(方案9)和自由場邊界(方案10)得到的點B響應加速度頻譜差別不大(圖8b)；黏性邊界(方案9)的PSA峰值略大于自由場邊界(方案10)(圖8c)，這是由于黏性邊界吸收不足，一部分波反射疊加引起的；黏性邊界計算所得的PSA在0.4 s～0.6 s區間大于自由場邊界的計算值，而在0.6 s～1.1 s區間則較小，這也是由邊界條件引起的。

a.方案9；b. 方案10。圖7 Rayleigh波+地震波作用下場地水平加速度云圖Fig.7 Cloud chart for horizontal acceleration of site under the effects of Rayleigh waves and seismic waves

Table3NumericalprocedureforstudyingtheinfluenceofdynamicboundaryconditionsunderthecombinedeffectsofRayleighwavesandbottomseismicwaves

方案模型尺寸激勵荷載動力邊界9100m×30mRayleigh波+底部加速度時程兩側黏性邊界;底部柔性地基邊界10100m×30mRayleigh波+底部加速度時程兩側自由場邊界;底部柔性地基邊界11150m×30mRayleigh波+底部加速度時程兩側自由場邊界;底部柔性地基邊界1250m×30mRayleigh波+底部加速度時程兩側自由場邊界;底部柔性地基邊界13100m×100m×30m底部加速度時程激勵左右兩側自由場邊界;其余側固定邊界

注：方案9—12為二維模型，模型尺寸為長×寬；方案13為三維模型，模型尺寸為長×寬×高。

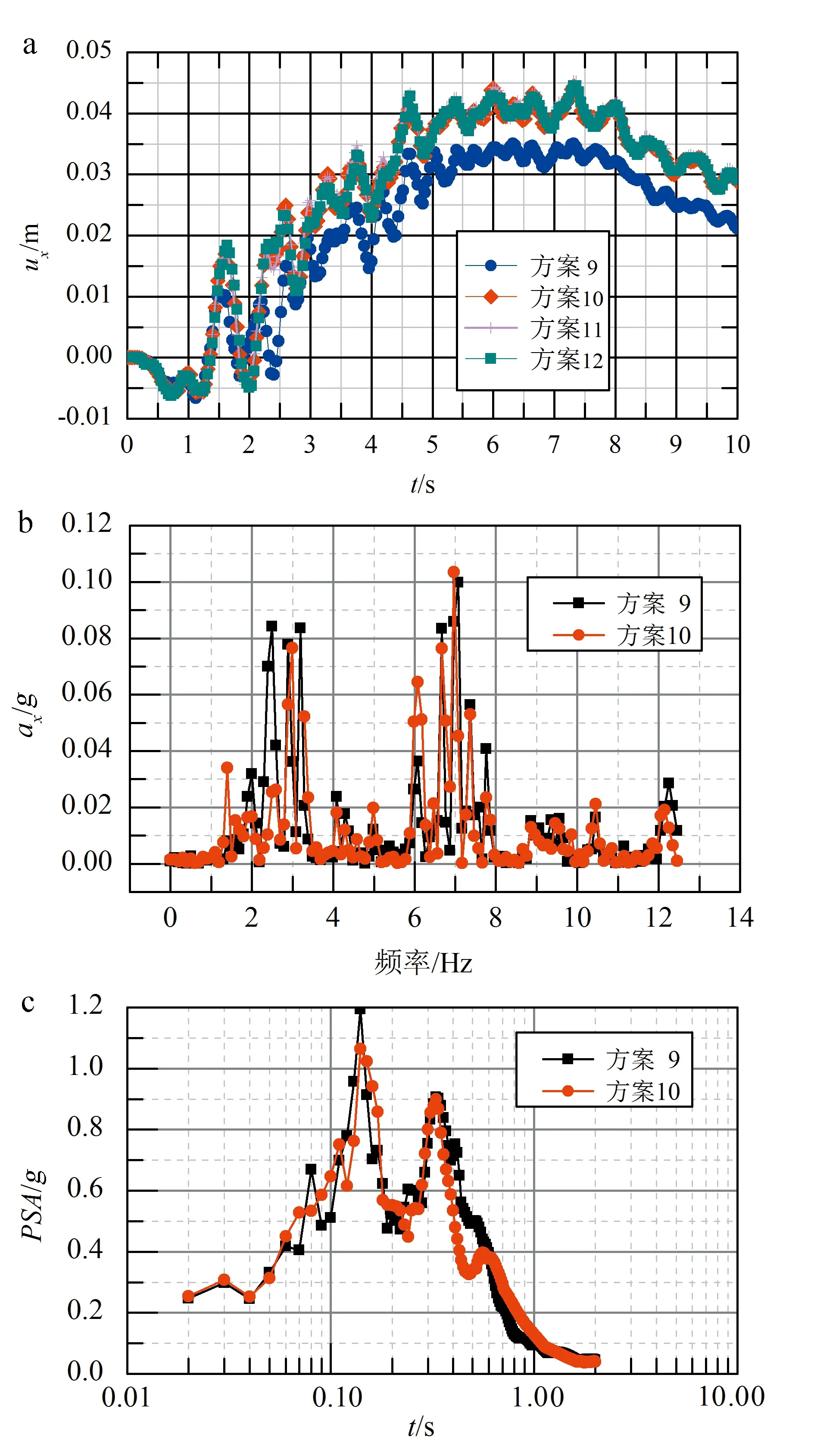
a.水平位移-時間曲線；b. 水平加速度頻譜曲線；c.水平加速度PSA曲線。圖8 Rayleigh波+地震波作用下點B(50,0)動力響應曲線Fig.8 Horizontal displacement-time curve for B (50, 0) under the effects of rayleigh dynamic response waves

在二維和三維模型中，通過不同高度的監測點輸出PSA加速度曲線，如圖 9所示。

從圖 9a可以看出，PSA加速度在0.04 s后逐步被放大，產生一定的波動后，最后減少至0。從圖 9b可以看出，在三維模型中存在同樣的效果，且中心點(50，50，0)PSA加速度曲線與二維能夠很好地對應。

5 Rayleigh波+底部地震波共同作用下動力邊界優化組合效果分析

5.1 計算方案

通過前述分析可知，單獨設置黏性邊界或自由場邊界，能夠在一定程度上實現波在模型邊界上的傳播和對反射的吸收，但效果還不夠理想。下面主要通過三維計算模型，研究Rayleigh波+底部地震波雙動力輸入作用下，采用黏性邊界、自由場邊界及固定邊界的組合設置人工邊界條件，研究土體本構為線彈性及彈塑性(如小應變硬化模型HSS)的綜合管廊對場地動力響應的影響，具體組合計算方案及邊界條件見表 4、表5。

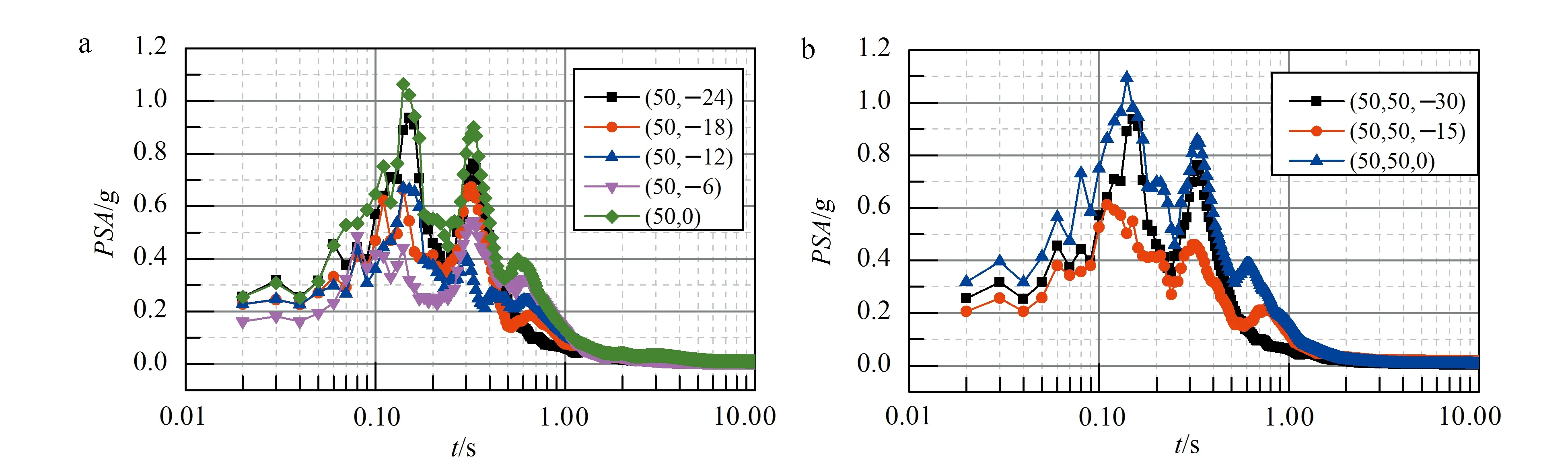
a.二維；b. 三維。圖9 Rayleigh波+地震波作用下不同高度監測點水平加速度PSA曲線Fig.9 Horizontal acceleration PSA curves for monitoring sites at different heights under the effects of Rayleigh waves and seismic waves

Table4NumericalprocedureforoptimizedcombinationofdynamicboundaryconditionsundertheeffectsofRayleighwavesandseismicwaves(linearelasticmodel)

方案模型尺寸激勵荷載動力邊界組合141516100m×100m×30m100m×100m×30m100m×100m×30mRayleigh波底部加速度時程Rayleigh波+底部加速度時程激勵側固定邊界,遠離激勵側黏性邊界,其余兩側自由場邊界

注：方案14—16均為三維模型，模型尺寸為長×寬×高。

表5Rayleigh波+底部地震波共同作用下動力邊界優化組合計算方案(HSS模型)

Table5NumericalprocedureforoptimizedcombinationofdynamicboundaryconditionsundertheeffectsofRayleighwavesandseismicwaves(HSSmodel)

方案模型尺寸激勵荷載動力邊界組合171819100m×100m×30m100m×100m×30m100m×100m×30mRayleigh波底部加速度時程Rayleigh波+底部加速度時程激勵側固定邊界,遠離激勵側黏性邊界,其余兩側自由場邊界

注：方案17—19均為三維模型，模型尺寸為長×寬×高。

5.2 計算結果

土體為線彈性模型時，Rayleigh波+底部加速度時程(方案16)共同作用下不同時刻的變形網格如圖 10所示。不同本構模型、不同邊界、不同動力作用下點A(50,50,0)的豎向位移時程曲線如圖 11所示。考慮土體彈塑性模型(HSS)條件下，底部地震波作用(方案18)下地基水平加速度云圖如圖 12所示。

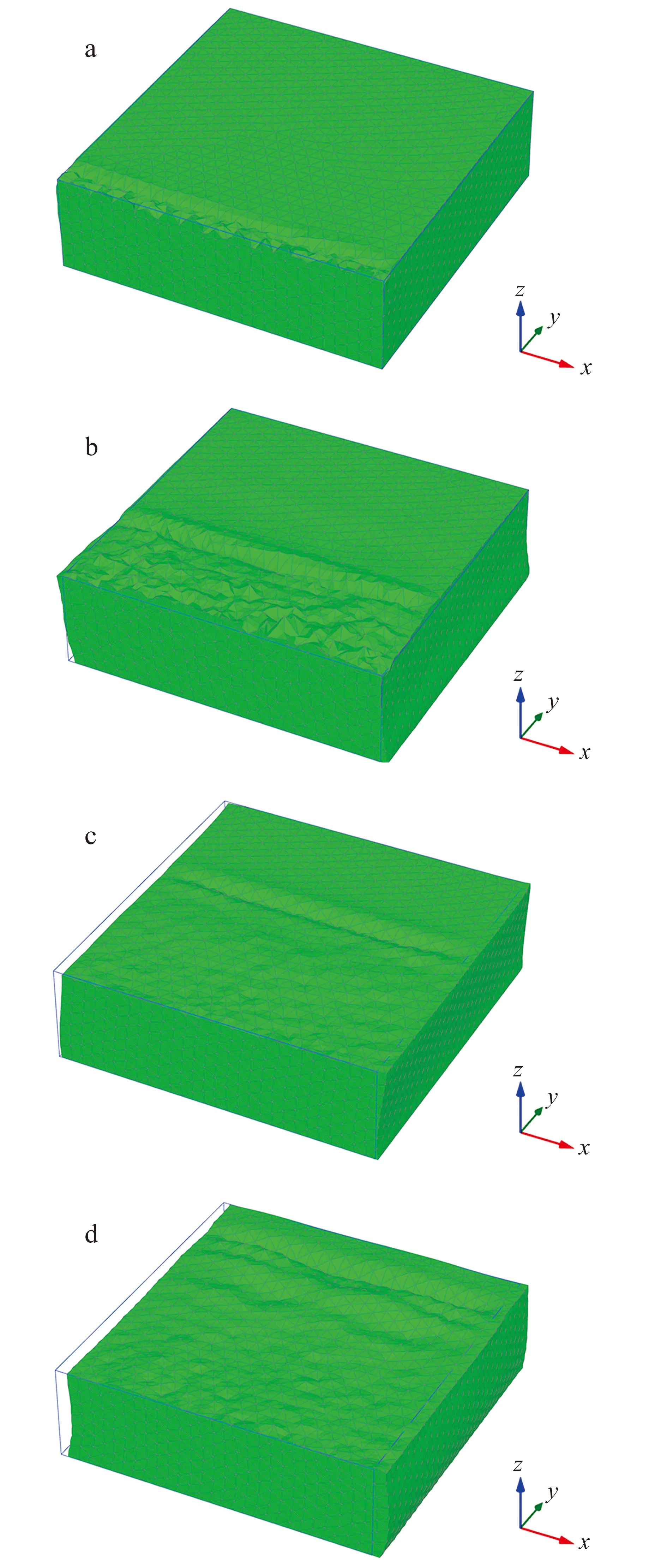
a.t=2.14 s；b.t=2.40 s ；c. t =2.66 s；d. t=2.92 s。圖10 Rayleigh波+底部地震波共同作用下在不同時刻網格變形特征Fig.10 Mesh deformation characteristics under the effects of Rayleigh waves and bottom seismic waves at different times

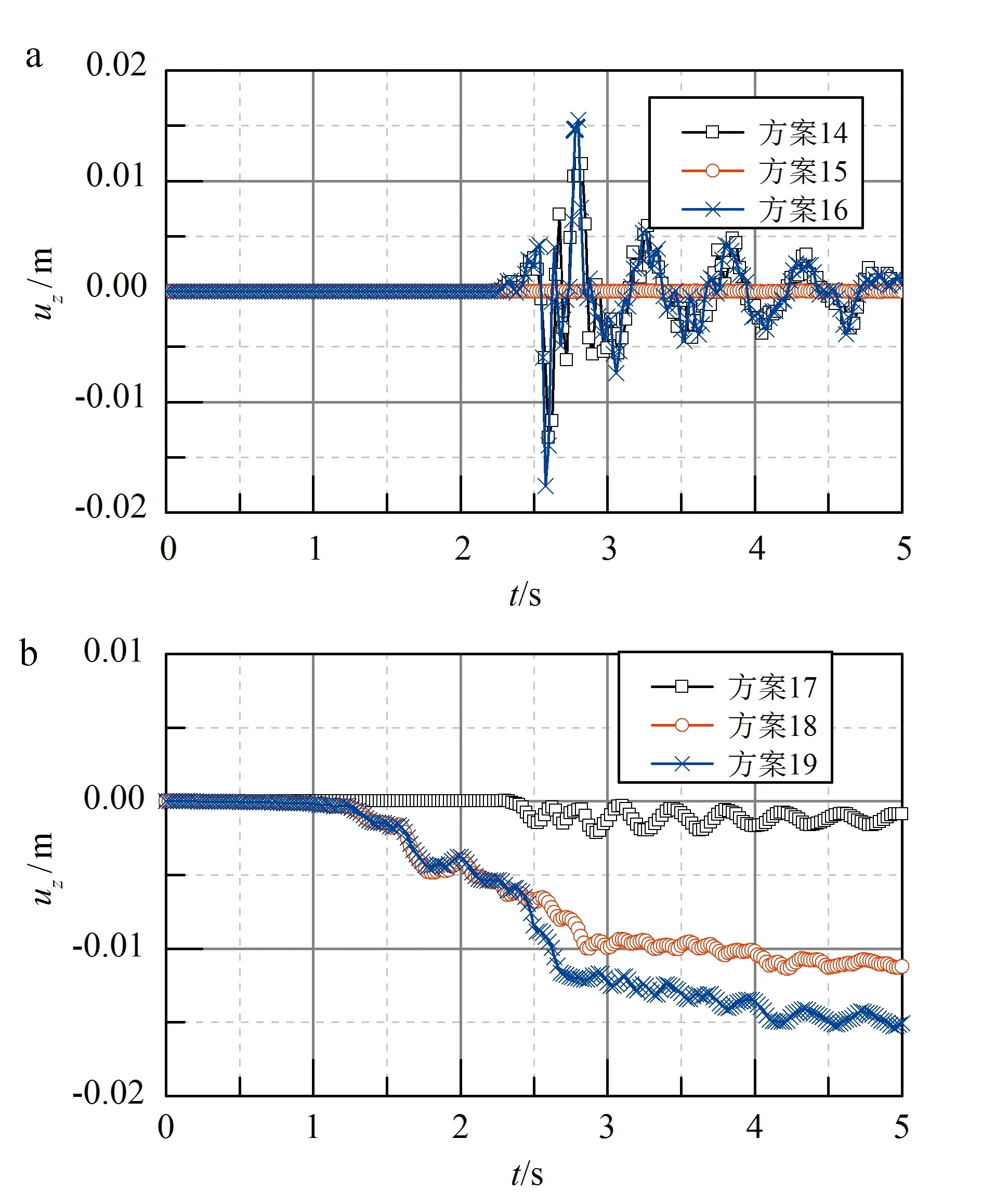
a.線彈性模型；b. HSS模型。圖11 Rayleigh波+底部地震波共同作用下點A(50,50,0)的豎向位移時程曲線Fig.11 Vertical displacement time history curve for A (50,50,0) under the effects of Rayleigh waves and bottom seismic waves

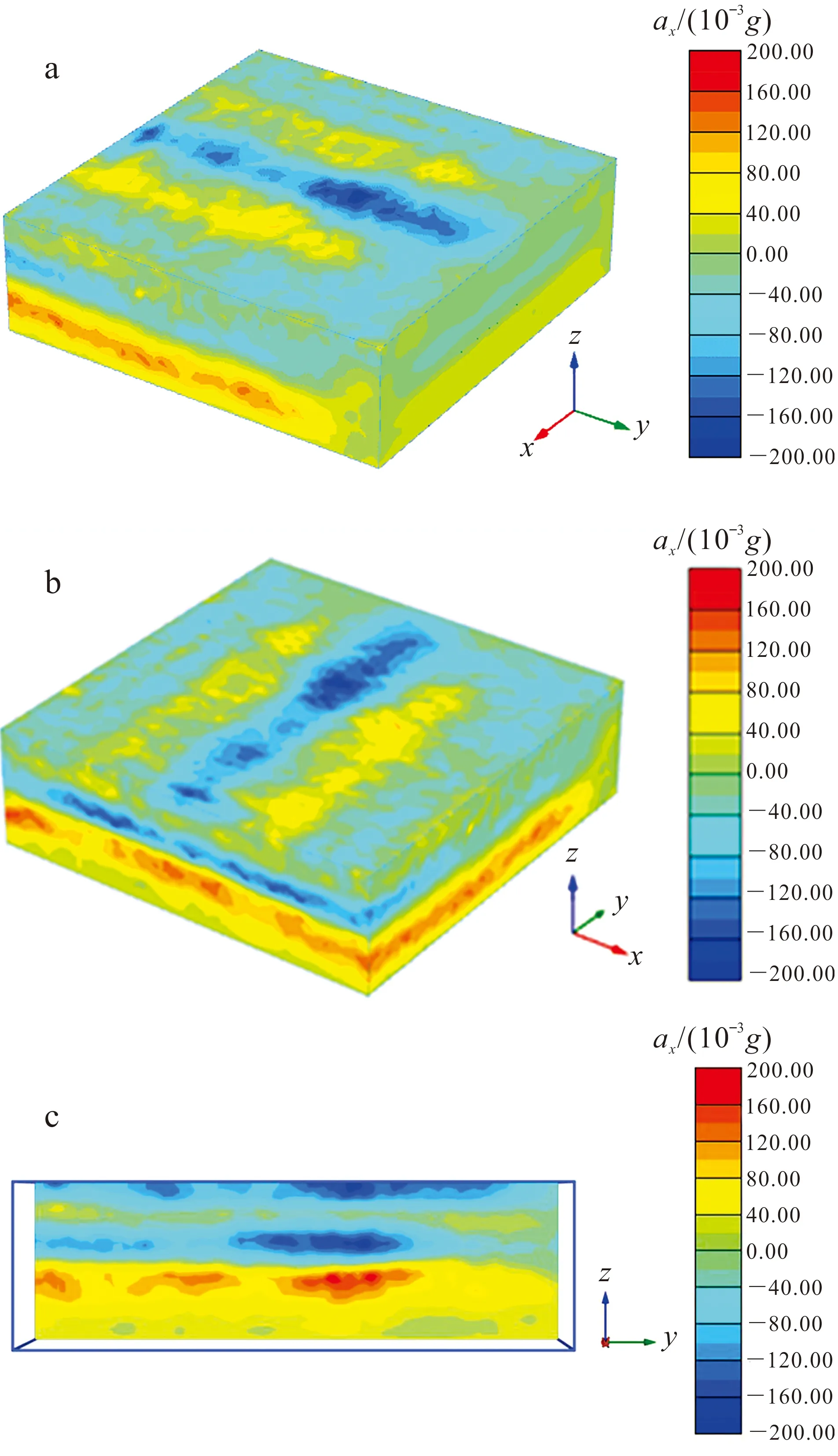
a.三維ax云圖，t =1.10 s，視角1；b. 三維ax云圖，t=1.10 s，視角2； c. 剖面ax云圖，t =1.10 s。a、b圖中，axmax=0.192 2g(單元14472在節點23474)，axmin=-0.192 7g(單元27662在節點26433)。圖12 優化動力邊界下地基水平加速度云圖Fig.12 Cloud chart for horizontal acceleration of foundation in optimized dynamic boundary conditions

由圖 10可以看出，當地基為線彈性體時，Rayleigh波和底部地震波的交叉干擾較少， Rayleigh波和底部地震波共同作用時均能夠得到較好的傳播，在模型邊界上能夠得到恰當的吸收和釋放，表明了此時邊界條件設置是有效的。圖 11a顯示，底部加速度時程(方案15)引起的模型表面中心點豎向位移基本可忽略；而單獨Rayleigh波作用下(方案14)與雙動力(Rayleigh波+底部加速度時程)輸入作用下(方案16)的該中心點的豎向位移基本一致，進一步表明線彈性條件下，使用該動力邊界，Rayleigh波與底部地震波引起的場地動力響應相互干擾很小，近似為線性疊加。

從圖 11b可以看出，Rayleigh波(方案17)引起的模型表面中心點豎向位移很小，底部地震波(方案18)引起的豎向位移占主導，雙動力輸入下(方案19)該中心點的豎向位移基本可視為Rayleigh波和地震波作用效果的線性疊加。這是由于HSS模型能夠反映土體的滯回阻尼特性，土體塑性變形隨著動力作用時間的推進產生了一定的累積增長，模型表面中心監測點豎向位移時程曲線的形態與彈性地基條件下有明顯差別。

對于類似HSS本構模型的彈塑性材料地基而言，分析Rayleigh波+底部地震波共同作用下的動力響應，采用上述邊界條件下也同樣適用。從圖 12可以看出：對于考慮土體小應變特性的彈塑性地基，計算模型y方向的最小值ymin(即激勵側)未設動力人工邊界，波的傳播受影響不大，加速度仍較大(云圖中藍色區域較大)；但是計算模型y方向的最大值ymax(即遠離激勵側)設置了黏性邊界，在邊界附近加速度快速衰減，(云圖中藍色區域幾乎沒有)可見黏性邊界造成了一定范圍內的能量吸收。

綜上所述，Rayleigh波和地震波這兩種動力輸入引起的場地動力響應(位移和加速度)可以按線性疊加處理，二者交叉干擾較小；從動力人工邊界的影響來看，黏性邊界對地震波引起的動力響應有一定范圍的吸收，自由場邊界對Rayleigh波引起的動力響應也有一定范圍的變形限制影響。在Rayleigh波和底部加速度時程共同作用下，可采用激勵側固定邊界、遠離激勵側黏性邊界、其余兩側自由場邊界的優化動力邊界。

6 結論

1)黏性邊界主要考慮對外行波的吸收效果，而沒有考慮地震動的輸入問題，在地震波(底部水平加速度時程)作用下，黏性邊界會對模型內部土體的水平位移產生限制作用而使得場地內水平位移響應偏小，自由場邊界則基本不存在這種限制作用，更適用于底部加速度時程引起的動力響應分析。

2)黏性邊界僅考慮了對散射波能量的吸收，并未考慮人工邊界外半無限介質的彈性恢復性能，在Rayleigh波作用下，黏性邊界對散射能量的吸收效果偏大，導致場地動力響應偏小，而采用自由場邊界時則表現出明顯偏大的強烈振蕩。相比之下，采用激勵側固定邊界、另一側黏性邊界的組合動力邊界設置能夠得到較好的場地動力響應結果，具有較好的收斂性。

3)基于激勵側固定邊界、遠離激勵側黏性邊界、其余側自由場邊界的優化組合動力邊界設置，在Rayleigh波和底部加速度時程共同作用下，二者引起的動力響應交叉干擾較少，可按線性疊加處理；同時，黏性邊界對地震波引起的動力響應有一定范圍的吸收，自由場邊界對Rayleigh波引起的動力響應也有一定范圍的變形限制影響。

4)計算Rayleigh波和底部加速度時程共同作用下，彈塑性地基的綜合管廊地震動力響應，邊界條件可設置為：激勵側固定邊界、遠離激勵側黏性邊界、其余側自由場邊界。

[1] 城市綜合管廊工程技術規范: GB 50838-2015[S]. 北京: 中國建筑工業出版社, 2015.

Technical Code for Urban Utility Tunnel Engineering: GB 50838-2015[S]. Beijing: China Architecture & Building Press, 2015.

[2] 莊海洋, 程紹革, 陳國興. 阪神地震中大開地鐵車站震害機制數值仿真分析[J]. 巖土力學, 2008, 29(1): 245-250.

Zhuang Haiyang, Cheng Shaoge, Chen Guoxing. Numerical Simulation and Analysis of Earthquake Damages of Dakai Metro Station Caused by Kobe Earthquake[J]. Rock & Soil Mechanics, 2008, 29(1): 245-250.

[3] Wolf J P， Song C. Some Cornerstones of Dynamic Soil -Structure Interaction[J]. Engineering Structures, 2002, 24(1): 13-28.

[4] 邱流潮, 金峰. 地震分析中人工邊界處理與地震動輸入方法研究[J]. 巖土力學, 2006, 27(9): 1501-1504.

Qiu Liuchao, Jin Feng. Study on Method of Earthquake Input and Artificial Boundary Conditions for Seismic Soil-Structure Interaction Analysis[J]. Rock & Soil Mechanics, 2006, 27(9): 1501-1504.

[5]Hatzigeorgiou G D, Beskos D E. Soil - Structure In-teraction Effects on Seismic Inelastic Analysis of 3-D Tunnels[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9) : 851-861.

[6] Ghandil M, Behnamfar F. The Near-Field Method for Dynamic Analysis of Structures on Soft Soils Including Inelastic Soil-Structure Interaction[J]. Soil Dynamics and Earthquake Engineering, 2015,75: 1- 17

[7] 張波, 李術才, 楊學英,等. 三維黏彈性介質人工邊界研究[J]. 巖土力學, 2009, 30(11):3469-3475.

Zhang Bo, Li Shucai, Yang Xueying, et al. Study of Three Dimensional Viscoelastic Medium Artificial Boundary[J]. Rock & Soil Mechanics, 2009, 30(11):3469-3475.

[8] 高峰, 關寶樹. 沉管隧道三維地震反應分析[J]. 蘭州交通大學學報, 2003, 22(1): 6-10.

Gao Feng, Guan Baoshu. Three-Dimensional Seismic Response Analysis of Immersed Tunnel[J]. Journal of Lanzhou Jiaotong University, 2003, 22(1): 6-10.

[9] 孫海峰, 景立平, 孟憲春,等. ABAQUS中動力問題邊界條件的選取[J]. 地震工程與工程振動, 2011, 31(3):71-76.

Sun Haifeng, Jing Liping, Meng Xianchun, et al. The Selection of Boundary Conditions in Dynamic Problems by Using ABAQUS[J]. Journal of Earthquake Engineering & Engineering Vibration, 2011, 31(3): 71-76.

[10] 劉志強, 孫建國, 孫輝, 等. 曲線坐標系下的完全匹配層吸收邊界條件[J/OL]. 吉林大學學報(地球科學版) (2017-03-23) [2017-09-28]. http://kns.cnki.net/kcms/detail/22.1343.p.20170323.1418.002.html.

Liu Zhiqiang, Sun Jianguo, Sun Hui, et al. A Perfectly Matched Layer Absorbing Boundary Condition Under the Curvilinear Coordinate System[J/OL]. Journal of Jilin University (Earth Science Edition), (2017-03-23) [2017-09-28]. http://kns.cnki.net/kcms/detail/22.1343.p.20170323.1418.002.html.

[11] Jiao Y Y, Zhang X L, Zhao J, et al. Viscous Bou-ndary of DDA for Modeling Stress Wave Propagation in Jointed Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 1070-1076.

[12] Deeks A, Randolph M. Axisymmetric Time-Domain Transmitting Boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1):25-42.

[13] 劉晶波, 呂彥東. 結構-地基動力相互作用問題分析的一種直接方法[J]. 土木工程學報, 1998, 31(3):55-64.

Liu Jingbo, Lü Yandong. A Direct Method for Analysis of Dynamic Soil-Structure Interaction[J]. China Civil Engineering Journal, 1998, 31(3):55-64.

[14] 劉晶波, 王振宇, 杜修力,等. 波動問題中的三維時域粘彈性人工邊界[J]. 工程力學, 2005, 22(6):46-51.

Liu Jingbo, Wang Zhenyu, Du Xiuli, et al. Three-Dimensional Visco-Elastic Artificial Boundaries in Time Domain for Wave Motion Problems[J]. Engineering Mechanics, 2005, 22(6):46-51.

[15] 谷音, 劉晶波, 杜義欣. 三維一致粘彈性人工邊界及等效粘彈性邊界單元[J]. 工程力學, 2007, 24(12) : 31-37.

Gu Yin, Liu Jingbo, Du Yixin. 3D Consistent Viscous-Spring Artificial Boundary and Viscous-Spring Boundary Element[J]. Engineering Mechanics, 2007, 24(12): 31-37.

[16] 張燎軍, 張慧星, 王大勝,等.黏彈性人工邊界在 ADINA 中的應用[J]. 世界地震工程, 2008, 24(1) : 12-16.

Zhang Liaojun, Zhang Huixing, Wang Dasheng, et al. The Application of Artificial Viscous-Spring Boundary in ADINA[J]. World Earthquake Engineering, 2008, 24(1): 12-16.

[17] 蔣新新, 李建波, 林皋. 邊坡場地條件下粘彈性人工邊界模型的地震輸入模式研究[J]. 世界地震工程, 2013, 29(4) : 126-132.

Jiang Xinxin, Li Jianbo, Lin Gao. Study on the Seismic Input Mode of Viscoelastic Artificial Boundary Under the Condition of Slope Site[J]. World Earthquake Engineering, 2013, 29(4) : 126-132.

[18] 朱志輝, 余志武, 吳方伯,等. 考慮衰減波特性的透射邊界及其實現[J]. 湖南大學學報(自然科學版), 2007, 34(12):1-5.

Zhu Zhihui, Yu Zhiwu, Wu Fangbo, et al. Research on the Artificial Boundary in the Soil-Structure Dynamic Interaction[J]. Journal of Hunan University (Natural Sciences), 2007, 34(12):1-5.

[19]Liu J, Lu Y. A Direct Method for Analysis of Dynamic Soil-Structure Interaction Based on Interface Idea[J]. Developments in Geotechnical Engineering, 1998, 83(3): 261-276.

[20] 權登州, 王毅紅, 井彥林, 等. 黃土區地鐵車站動力分析中的無限元傳輸邊界[J]. 西安建筑科技大學學報(自然科學版), 2015, 47(4):537-542.

Quan Dengzhou, Wang Yihong, Jing Yanlin, et al. Infinite-Element Transmitting Boundary in Dynamic Analysis of Subway Station in Loess Area[J].Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2015, 47(4):537-542.

[21] Seed H B, Martin P P, Lysmer J. The Generation and Dissipation of Pore Water Pressures During Soil Liquefaction[R]. Oakland: University of California, 1975.

[22] 付曉東, 盛謙, 張勇慧. DDA方法中的人工邊界問題研究[J]. 巖石力學與工程學報, 2015(5):986-993.

Fu Xiaodong, Sheng Qian, Zhang Yonghui. Investigation on Artificial Boundary Problem in Discontinuous Deformation Analysis Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 986-993.

[23] 鐵路工程抗震設計規范 GB50111-2006[S]. 北京: 中國計劃出版社, 2006.

Code for Seismic Design of Railway Engineering: GB50111-2006[S]. Beijing: China Planning Press, 2006.

[24] 建筑抗震設計規范 GB50011-2001[S]. 北京: 中國建筑工業出版社, 2001.

Code for Seismic Design of Building GB50011-2010[S]． Beijing: China Architecture & Building Press，2001．

[25]Lamb H. On the Propagation of Tremors over the Surface of an Elastic Solid[J]. Philosophical Transactions of the Royal Society of London, 1904, 203,359:1-42.

[26] Shi Youzhi. Contribution of Rayleigh Damping Para-meters to Site Response Under Influence of Rayleigh Wave[J]. Revista Tecnica De La Facultad De Ingenieria Universidad Del Zulia, 2016, 39(6): 48-59.