基于半監督核均值漂移聚類的地震相識別研究

郝茜茜 ，周亞同 ，任婷婷

0 引言

地震相識別是地震層序劃分的前提，是油氣藏勘探和儲層預測的基礎[1].在地震剖面上包含著豐富的地質信息，已有很多聚類方法被用于地震相識別.例如K均值[2]，模糊C均值聚類[3]，DBSCAN聚類[4]，但上述都是一些常規的聚類方法.

近年又涌現了一些性能優良的聚類方法.例如SOM聚類[5]，次勝者懲罰競爭學習聚類[6]和均值漂移聚類.均值漂移[7]是一種基于非參數估計的密度聚類算法，通過迭代搜索特征空間中的樣本點，使聚類中心始終向密度最大的方向移動.該算法迭代速度快，無需人為規定聚類個數且可以對任何的集群結構聚類，Subbarao等[8]和Vedaldi等[9]實現了均值漂移在核空間的聚類.此方法被廣泛應用于目標跟蹤[10]、圖像分割[11-12]、圖像去霧[13]和廣播音頻[14]等方面，但目前為止還未被用于地震相識別.

半監督學習是近年來較受關注的方法之一，通過將半監督學習與一些常規聚類方法結合，應用少量的先驗信息去指導聚類過程以使聚類結果更準確.例如林超[15]通過對半監督學習方法與k均值聚類結合，解決了算法的約束違反問題.Kulis等[16]將半監督學習與圖譜聚類結合優化了圖形數據聚類.尹學松等[17]先根據成對約束得到投影空間后在投影空間進行k均值聚類，然后在由線性判別法得到的子空間中再次聚類.Tuzel等[18]和Anand等[19]實現了半監督學習與核聚類法的結合.

核均值漂移聚類不局限于集群結構的類型，適用于復雜多變的地震數據結構，半監督學習又可以根據已知的先驗信息指導聚類過程.基于以上考量，本文研究基于半監督核均值漂移聚類（SKMS）的地震相自動識別算法.理論數據模型和實際地震數據聚類均表明SKMS是一種有效的地震相劃分方法.

1 核均值漂移（KMS）聚類原理

在核均值漂移（KMS）聚類中，歐式空間擴展為一般的內核空間.令χ為輸入空間，則有n個樣本xi∈χ，i=1，…，n.假設空間 χ表示為 Rd，x 通過映射函數 φl，l=1，…，dφ映射到 dφ維特征空間 H，即

定義對角帶寬矩陣為hiIdφ×dφ，i=1，…，n，y∈H，則在特征空間H中的核密度估計為

對公式（2）求梯度可得空間H中的均值漂移向量為

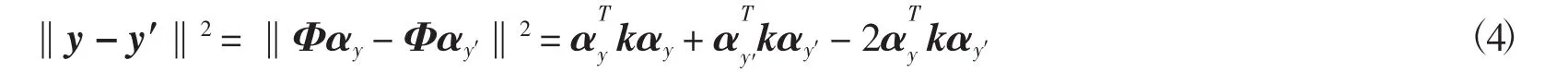
定義ei為特征空間H中的第i維標準基向量，有ei∈Rn，則φ（xi）=Φei，將此式與式（4）代入式（3）中有

從而可以得到均值漂移向量，該方法同樣收斂于局部分布模式.這樣通過賦予合適的映射函數就可以實現核均值漂移聚類.

2 半監督均值漂移（SKMS）聚類原理

在核均值漂移算法的基礎上，該算法采用成對約束來指導聚類過程.在聚類之前，需要根據先驗經驗采集must-link和cannot-link約束組成成對約束.聚類過程為：首先將所有點通過核函數映射到高維空間中，然后在高維核空間中對所有成對約束進行線性變換，最后將特征點全部投影到約束向量零空間，使兩點之間距離符合距離目標參數的聚為一類.

2.1 通過更新核函數實現線性變換

對樣本進行變換，就是將樣本從特征空間向約束向量的零空間投影的過程，此過程可以通過更新式（5） 中的核矩陣隱形實現.定義（j1，j）2為成對約束，表示j1，j2被強制成為一對，既可以是must-link成對約束也可以是cannot-link成對約束，有.若給定nc個成對約束NC，dφ維的約束向量可以表示為其中n維向量zj表示為第j個成對約束的指標向量，則含nc個約束向量的約束矩陣A=ΦZ，其中Z= [z1，z2，…，znc]為n×nc階指標矩陣.定義線性變換矩陣為

其中：s為a的縮放因子.當s=1/aTa時，該變換就變為從特征空間向約束向量a的零空間投影；當0〈s〈2/aTa時，該變換減小成對點之間的距離；當s〈0或s>2/aTa時，該變換增大成對點之間的距離.

令成對點的距離為d>0，則有

將約束向量a=Φz代入到公式（8）中得

2.2 通過logdet布雷格曼散度實現核函數更新

布雷格曼散度是一種類似距離度量的方式.若有n×n維的矩陣X和Y，則有布雷格曼散度公式如下

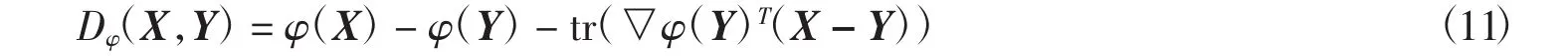
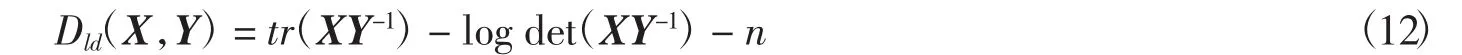
其中：X和Y為半正定矩陣且X和Y的秩不大于n.對X和Y進行奇異值分解，有X=V∧VT，Y=UΘUT，進而可以求得logdet布雷格曼散度

現通過logdet布雷格曼散度實現核函數更新.給定m個must-link成對約束集M和n個cannot-link成對約束集C，有m+c=nc.must-link約束的目標距離為dm，cannot-link約束的目標距離為dc，則最終的更新核矩陣問題轉化為求logdet布雷格曼散度最小化問題，即目標函數為

由于在logdet布雷格曼散度中的第一個參數X要求必須是凸的，用logdet散度最小化更新核矩陣可以保證算法收斂到全局最優解.

3 應用SKMS進行地震相識別的步驟

用SKMS進行地震相識別的步驟如圖1所示.對于給定地震數據，首先進行地震屬性提取和歸一化，然后對優選后的地震屬性采用SKMS聚類法得到地震相識別結果.

在圖1中需要用到SKMS聚類，它的具體步驟為：

圖1 用SKMS進行地震相識別的步驟Fig.1 The steps of seismic facies identification using SKMS

步驟1：各參數初始化.初始化約束距離參數dm和dc，dm為must-link約束初始距離，dc為cannot-link約束初始距離；初始化成對約束集M和C；

步驟2：計算初始核矩陣k；

步驟3：采用logdet散度更新核矩陣k?；

步驟4：對于地震屬性的n個樣本點i=1，2，…，n

4 實驗結果與分析

為了驗證SKMS聚類效果，分別對理論模型和實際地震數據進行處理，將處理結果與k均值聚類、核k均值聚類（KK聚類）、譜聚類[20]、均值漂移聚類（MS聚類）、全局核k均值聚類（GKK聚類）[21]和自組織神經網絡聚類（SOM聚類）等算法對比.

4.1 理論數據模型實驗

在地質結構中通常含有褶皺、尖滅和套疊等結構單元.首先理論模擬出這3種結構，并采用SKMS聚類，然后將這3種理論結構模型采用上述5種算法對之聚類.聚類結果如圖2～圖4所示.

實驗1：褶皺結構如圖2所示.

圖2 褶皺結構的各種算法聚類結果Fig.2 The clustering results of various algorithms for folds

實驗2：尖滅結構如圖3所示.

圖3 尖滅結構各種算法聚類結果Fig.3 The clustering results of various algorithms for pinch-out

實驗3：套疊結構如圖4所示.

圖4 套疊結構的各種算法聚類結果Fig.4 The clustering results of various algorithms for telescope

表1 理論數據模型的詳細信息Tab.1 Detailed information on theoretical data models

表2 各算法運行時間對比Tab.2 Comparison of running time of each algorithm

表3 各聚類算法準確率對比（CA）Tab.3 Accuracy ratio of each algorithm （CA）

從表2看出，SKMS總體比KK、MS、K的運行時間長，但與GKK相比，總體運行時間短.在樣本個數為202時，譜聚類的時間比SKMS長，隨著樣本個數的增長，SKMS比譜聚類的運行時間的增長速度快.對聚類結果的評價標準，本文采用準確性（cluster accuracy，簡稱CA）度量.從表3可以觀察到：SKMS的聚類準確性明顯優于其它的幾種算法，SKMS在不同的理論模型上的準確性均達到了90%以上.而且SKMS在計算時均能正確估計聚類個數.

4.2 實際地震數據實驗

本實驗采用荷蘭北海F3地震數據.在opendtect6.0和Matlab2013a軟件平臺下采用傾角控制中值濾波后的地震數據進行運算.選取聯絡測線1 000縱剖面，剖面范圍為主測線的450-550道，時間線time的1724-1820部分，該縱剖面存在明顯的波形反射構型.

從地震屬性中選取相關系數較小的瞬時振幅、瞬時頻率、瞬時相位屬性，將這3種地震屬性作歸一化處理.應用這3種屬性，采用SKMS對屬性聚類，選取了3類共30個點如下所示，將這些點組成成對約束并采用SKMS聚類，效果如圖5所示.

圖5 SKMS聚類效果Fig.5 SKMS clustering result

在聯絡剖面1 000中，共標記了3類數據，如圖5a）所示，因截取的剖面數據為25×101，即共有2 525個地震數據，所以標簽數據占總地震數據數的1.19%，在SKMS聚類中，可以生成個mustlink成對約束，然后再構造同樣個數的cannot-link成對約束，選取高斯核函數，其中σ為0.5，SKMS聚類將地震相劃分為6類，如圖5b）所示.

同樣應用上述3種屬性，分別采用不同的方法聚類，結果如下所示.

在KK聚類、譜聚類和GKK聚類中，均采用同一個高斯核函數，σ取0.5，聚類個數設為6類，如圖6 a） ～圖6 c） 所示.在MS聚類中，帶寬值為2.5，聚類結果為6類，如圖6 e） 所示.k均值聚類結果如圖6 f）所示.SOM聚類為商業軟件的聚類效果.SKMS與其他算法的聚類效果相比，層次更分明，層與層之間的邊界清晰，在綠圈范圍內，能夠將一些微小地層區分出來.

圖6 各算法聚類效果Fig.6 clustering results of each algorithm

5 結論

本文采用SKMS對地震屬性聚類，利用已知的少量先驗信息對聚類過程約束，達到提高地震相劃分結果的精確性的目的.均值漂移屬于密度聚類，能夠自動優化判斷聚類個數，且可以對任意數據結構都有效.SKMS聚類法融合了MS聚類和半監督聚類的優勢，將SKMS聚類與其他聚類算法相比，比無監督聚類的聚類結果準確度有了很大提高，劃分地震相的層次更分明.

[1] Robert E.Sheriff.Structural interpretation of seismic data[M].American：American Association of Petroleum Geologists，1982：14.

[2] 龐銳，魏嘉.利用K均值聚類方法進行地震相識別[C]//臧紹先.中國地球物理學會第二十四屆年會論文集.北京：中國地球物理學會.2008：132.

[3] 張陽，邱隆偉，李際，等.基于模糊C均值地震屬性聚類的沉積相分析[J].中國石油大學學報自然科學版，2015，39（4）：53-61.

[4] 楊瑞超.DBSCAN算法在地震相劃分中的應用[D].西安：西安科技大學，2011：1-43.

[5] 張龔，鄭曉東，李勁松，等.基于SOM和PSO的非監督地震相分析技術[J].地球物理學報，2015，58（9）：3412-3423.

[6] Zhan Shifan，Lei Li，Wei Xiong，et al.Automatic geological body identification using the modified rival penalized competitive learning clustering algorithm[C]//Seg Technical Program Expanded.USA：Society of Exploration Geophysicists.2011：4424

[7] Cheng Yizong.Mean Shift，Mode seeking，and clustering[J].Pattern Analysis&Machine Intelligence IEEE Transactions on，1995，17（8）：790-799.

[8] Subbarao R，Meer P.Nonlinear mean shift for clustering over analytic manifolds[C]//Jean-Philippe Tardif.IEEE Computer Society Conference on Computer Vision and Pattern Recognition.USA：IEEE Computer Society，2006：1168-1175.

[9] Vedaldi Andrea，Soatto Stefano.Quick shift and kernel methods for mode seeking[M].France：Computer Vision-ECCV 2008，2008：705-718.

[10]馬麗，常發亮，喬誼正，等.基于改進的均值漂移算法的目標跟蹤[J].計算機工程，2006，32（24）：175-177.

[11]伍艷蓮，趙力，姜海燕，等.基于改進均值漂移算法的綠色作物圖像分割方法[J].農業工程學報，2014，30（24）：161-167.

[12]白培瑞，李良，趙奇，等.基于均值漂移的醫學超聲圖像分割改進算法[C]//中國智能自動化會議.南京：中國自動化學會，2009：1426-1431.

[13]陸海俊，汪榮貴，楊娟，等.基于均值漂移的暗原色先驗圖像去霧算法[J].合肥工業大學學報自然科學版，2016，39（9）：1205-1210.

[14] 鄭繼明，俞佳.基于 Mean-Shift的廣播音頻聚類算法[J].計算機應用，2009，29（10）：2741-2743，2750.

[15]林超.基于成對約束的半監督聚類算法研究及其并行化實現[D].西安：西南交通大學，2013：1-51.

[16]Kulis Brian，Basu Sugato，Dhillon Inderjit，et al.Semi-supervised graph clustering：a kernel approach[J].Machine Learning，2009，74（1）：1-22.

[17]尹學松，胡恩良，陳松燦.基于成對約束的判別型半監督聚類分析[J].軟件學報，2008，19（11）：2791-2802.

[18]Tuzel O，Porikli F，Meer P.Kernel methods for weakly supervised mean shift clustering[C]//IEEE，International Conference on Computer Vision，ICCV 2009，Kyoto，Japan，September 27-October.DBLP，2009：48-55.

[19]Anand Saket，Mittal Sushil，Tuzel Oncel，et al.Semi-supervised kernel mean shift clustering[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2014，36（6）：1201-15.

[20]Choromanska A，Jebara T，Kim H，et al.Fast spectral clustering via the Nystr?m method[M].Germany：Algorithmic Learning Theory.Springer Berlin Heidelberg，2014：367-381.

[21]Chen W Y，Song Y，Bai H，et al.Parallel spectral clustering in distributed systems[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2011，33（3）：568-586.