利用小波變換對MEMS矢量水聽器信號處理

尚珍珍，張國軍，韓建軍，丁俊文，楊晟輝

(中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原 030051)

0 引 言

矢量水聲傳感技術是檢測水中聲能流方向與強度的一種新技術，其信號處理技術是水聲工程領域令人矚目的研究方向之一，利用矢量傳感器能獲取水下聲矢量信號[1]，為信號檢測提供豐富的聲場信息[2]。隨著矢量傳感器[3]制作工藝不斷進步及其優越性的體現，基于矢量傳感器和矢量陣列的信號處理技術也得到越來越多的研究和應用。目前在這方面占據領先地位的是俄羅斯、美國和中國。

但是由于外場試驗環境的復雜性，很難對目標做出一個準確的估計，同時采集到的聲源信息含有大量噪聲，所以對信號進行有效降噪估計，進而結合相應的方位估計算法估計方位角就非常重要，之前對信號的處理都是直接進行傅里葉變換，簡單時頻分析，在強噪背景下信號的特征就不明顯，計算的方位角也不太準確，所以本文提出用小波變換進行信號的降噪處理，盡可能的保留信號更多的有用信息，降低噪聲的干擾。水聲信號處理的目的是為了對接收到的目標信號做出估計，更好的得到目標方位信息。目前研究小波降噪[4]方面的文章比較多，但通過對比傅里葉變換降噪和小波降噪，并通過有力的數據來證明小波降噪優越性方面的文獻目前還比較少。

本文以MEMS矢量水聽器為硬件依托，研究單矢量水聽器信號處理的基本問題，結合小波降噪通過理論分析、計算機仿真和湖試實驗驗證MEMS水量水聽器的定向性能，為后續的工程化應用及發展奠定基礎。

1 水聲信號獲取及定位原理

1.1 信號的獲取

納機電矢量水聽器是中北大學自行研制的新概念的矢量水聽器，融合MEMS技術、仿生原理和水聲原理[5]。其微結構三維示意圖如圖1所示。

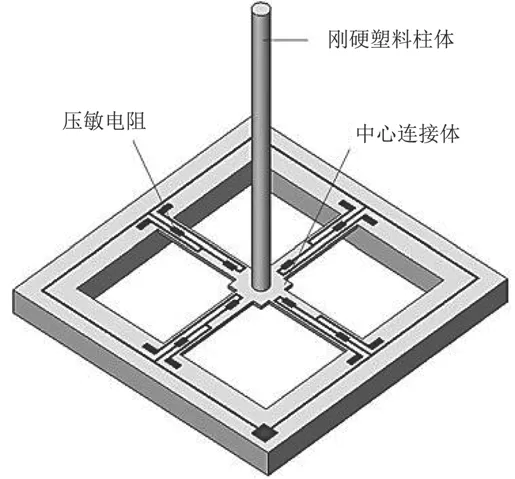
圖 1 微結構示意圖Fig. 1 Microstructure diagram

在測量范圍內，矢量水聽器可以接收任何類型的聲音信號，包括噪聲和目標信號，而對于信號處理僅對目標信號感興趣，這就需要從噪聲中分離出所需信號，降噪技術顯得很重要。

1.2 水聲定位原理

由聲學理論可知平面波聲壓可表示為：

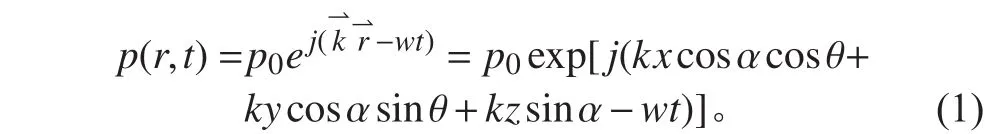
式中：k為波矢[量，表]示聲波傳播的方向，它與水平面的夾角為，它在水平面內的投影與x軸的夾角為，如圖2所示。

在均勻介質中，聲場的運動方程為：

平面波的聲壓與質點振速[6]三分量之間僅差一個常數，兩者的波形一樣，因而對平面波來說，聲壓與振速完全相關。可得質點振速的3個分量：

圖 2 波矢量在直角坐標系中的投影Fig. 2 Projection of wave vector in cartesian coordinate system

由此可見，只要測得質點振速在水平面內的2個分量vx、vy（水聽器測試的信號為電壓信號，正比于振速分量），就可以由上式得到聲源在水平面內的方位角θ，這就是矢量水聲傳感器確定聲源方位的基本原理。

但實際接收到的信號中包含很多噪聲，所以本文提出用傅里葉變換及小波變換對信號進行處理，為后續定位定向做好準備。

2 不同降噪方法

水聲信號一般是按1/3倍頻程發射的連續單頻正弦波，由于MEMS矢量水聽器的共振峰在1 kHz左右，所以主要研究500～800 Hz范圍內的信號。用信噪比來衡量一種方法的降噪性能。信噪比公式如下：

其中：S為信號功率；N為噪聲能量功率。

2.1 傅里葉變換

結合Matlab軟件[7]用傅里葉變換對信號進行簡單處理，通過直接法和Pwelch法求信號的功率譜密度。

直接法又稱周期圖法，它是把隨機序列x(n)的N個觀測數據視為一能量有限的序列，直接計算x(n)的離散傅里葉變換，得X(k)，然后再取其幅值的平方并除以N，作為序列x(n)真實功率譜的估計。

對于直接法的功率譜估計，當數據長度N太大時，譜曲線起伏加劇，若N太小，譜的分辨率又不好，因此需要改進。Pwelch法將N點的有限長序列x(n)分段求周期圖再平均。一是選擇適當的窗函數w(n)，并在周期圖計算前直接加進去，加窗的優點是無論什么樣的窗函數均可使譜估計非負。二是在分段時，可使各段之間有重疊，這樣會使方差減小。在Matlab上可用這2種方法進行功率譜的計算。

2.2 小波閾值降噪

小波分析是在傅里葉分析的基礎上發展起來的，但小波分析有著極大的不同，小波變換是空（時）間和頻率的局部變換，能有效從信號中提取信息。通過伸縮和平移等運算功能可對信號進行多尺度的細化分析[8]，解決了Fourier變換不能解決的許多問題。

設Ψ是定義在（-∞，∞）上能量有限的函數，Ψ構成平方可積信號空間，記為Ψ∈L2（R），則生成函數族{Ψab}：

Ψ(t)稱為小波函數，Ψab(t)由Ψ(t)伸縮和平移生成，是小波基函數。a為伸縮因子，b為平移因子。對任一信號f(t)∈L2(R)的連續小波變換可定義為信號與小波基函數的內積。從信號學的角度看，小波去噪是一個信號濾波的問題。盡管在很大程度上小波去噪可以看成是低通濾波。但由于在去噪后，還能成功地保留信號特征，所以在這一點上又優于傳統的低通濾波器。

小波去噪主要過程：

1）對接收到信號進行小波分解變化；

2）對小波系數作閾值門限處理（軟硬閾值）；

3）處理過的小波系數作逆變換重構信號，可得到去噪后的信號。

不同小波基以及閾值，對信號產生不同的處理效果。經過試驗，選擇“db4”，“sym8”這2種小波進行處理，使用4種閾值選取規則進行處理。

3 仿真研究

Matlab中的小波工具箱提供了小波變換的一些基本功能，仿真實驗及外場測試結果實現都在Matlab中進行，首先仿真正弦信號加入不同信噪比的高斯噪聲，通過相應算法處理，得出信噪比及誤差的具體對比。之后將仿真使用的信號處理方法用來處理外場信號。

3.1 FFT與小波降噪對比

含高斯噪聲的正弦信號，輸入信噪比分別為0、10，在Matlab中進行仿真并用FFT濾波及小波降噪[9]處理，選擇不同小波閾值。對比信號圖如圖3所示。

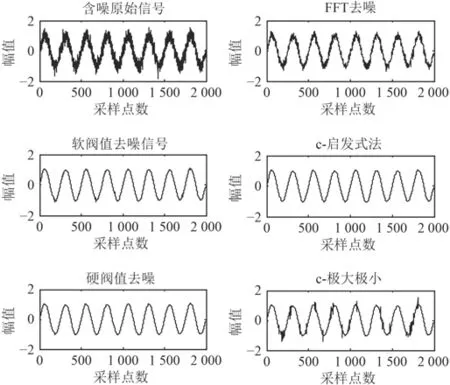
圖 3 Fft及4種小波閾值降噪方法Fig. 3 Fft and four kinds of wavelet threshold denoising methods

從信號圖看出小波降噪效果明顯優于Filter濾波，輸出信噪比及均方差具體比較見表1。

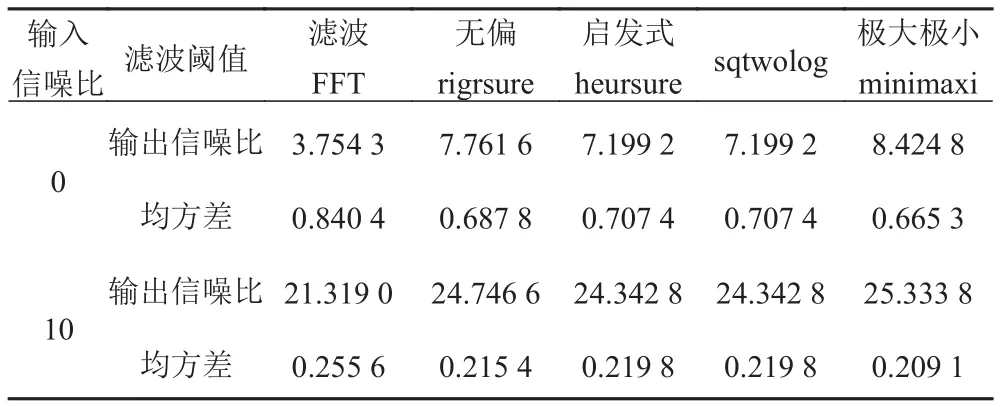
表 1 輸出信噪比及均方差Tab. 1 Output signal to noise ratio and mean square error

小波法對信噪比有很大的提高，當信噪比為10時，經小波不同閾值濾波提高了24 dB左右，而Filter濾波將信噪比提高到21 dB，小波法效果好；同時小波去噪后方差低于Filter濾波，所以小波對信號處理有很好的作用，不同閾值規則下效果區別不太大。

3.2 不同小波降噪對比

在Matlab中，設置入射信號為500 Hz正弦信號，添加隨機高斯噪聲，對比信號特征，目標信號為500 Hz線譜，噪聲分布在整個頻率范圍。可以通過小波變換把隨機噪聲濾掉，保留單頻信息。經過多次實驗發現db4和sym8小波對此目標信號濾波作用較好，同時使用heursure啟發式閾值規則，對信號進行處理，2種方法的輸出信噪比如表2所示。

對比圖表發現，使用同一種閾值規則，不同小波基處理的結果略有不同，sym8小波在相同輸入信噪比條件下，輸出信噪比高于db4小波，同時均方差也小，降噪效果更好。不論輸入信噪比如何，2種方法的輸出信噪比都有很大提升，信噪比為負時，均方差相對大些。所以對小波的研究很有待深入。

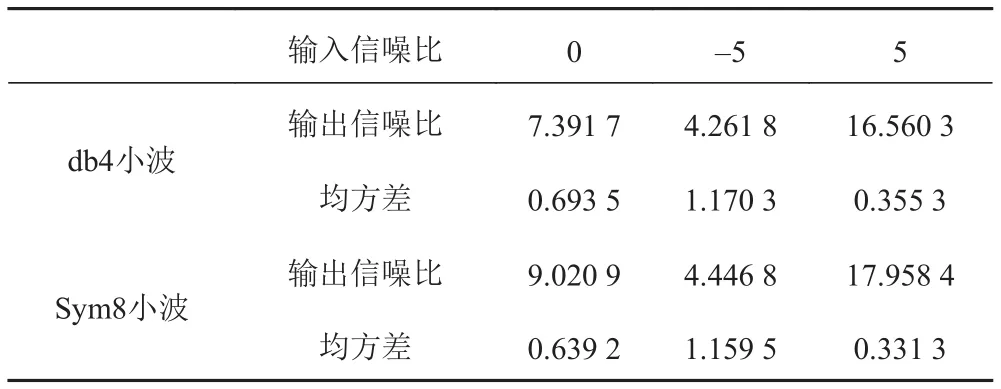
表 2 db4和sym8小波輸出信噪比及均方差Tab. 2 The signal-to-noise ratio and mean square error of db4 and sym8 wavelet output

4 外場試驗處理

在太原某水庫進行湖試試驗，實驗方案如圖4所示，魚唇換能器作為聲源，發射連續正弦信號，調整聲源與水聽器的間距約為15 m，換能器與水聽器放置在水面同一高度。實驗過程中，利用NI采集卡采集數據，采樣率設為4 kHz。調整水聽器的位置，使得聲波入射角為45°，驗證單矢量水聽器的目標定向能力[10]。

圖 4 湖試現場Fig. 4 Lake test site

二維矢量水聽器可以接收到X，Y兩路聲壓信號，設定采樣率為4 kHz，實時地進行信號采集，將采集到的數據用Matlab進行處理，畫出時頻信號，從圖5可以看出發射的是500 Hz的信號，第1行為兩路時域信號，第2行為直接傅里葉變換后頻域信息，第3行為功率譜密度。由于矢量水聽器的“8”字余弦指向性，從時域波形看出，由于外場環境的復雜性及不穩定性，信號含有很多的噪聲成分，所以首先對信號進行簡單濾波。

先窄帶濾波，再進行小波變換；降噪信號及功率譜密度如圖6和圖7所示。

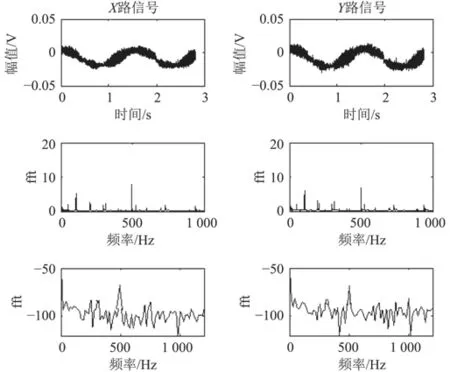
圖 5 湖試信號Fig. 5 Lake test signal

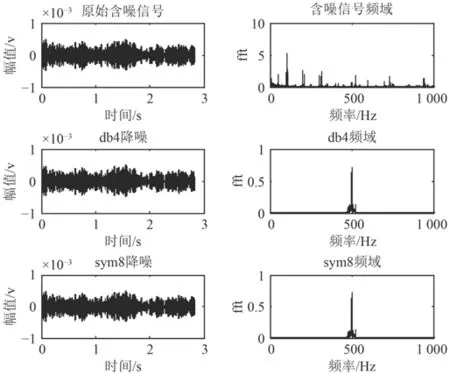
圖 6 湖試信號降噪時頻信息Fig. 6 Lake test signal noise reduction time-frequency information

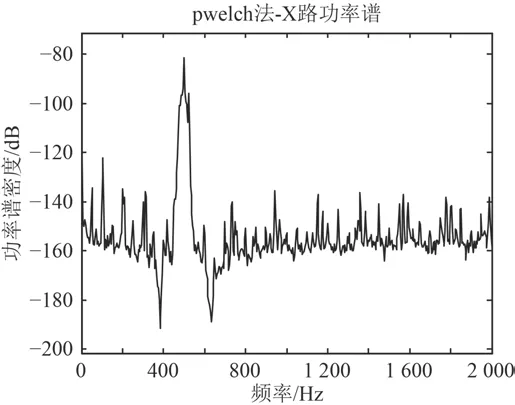
圖 7 降噪后X路信號功率譜密度Fig. 7 Noise density of X-channel signal after noise reduction

分析降噪后時頻信號，高頻部分的噪聲被濾掉一部分，低頻（100 Hz左右）附近的線譜是發射換能器自身的電噪聲及共頻干擾，原則上可以直接加窗濾掉這部分信號。經過小波變換及窄帶濾波處理，信噪比得到提升。因為多次室內及外場試驗使用的都是單矢量水聽器，而且使用一個魚唇換能器，所以目標聲源個數為1，當有多個聲源時可以用蓋氏圓盤法確定信號源數，這里就不詳細論述聲源數目的計算算法。

最后使用降噪后信號進行方位估計，結合直方圖法估計出方位角，具體原理如圖8所示。

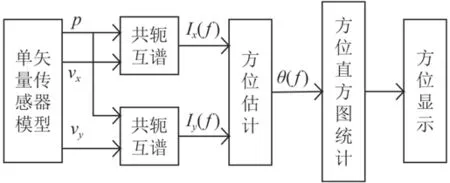
圖 8 直方圖方位估計原理圖Fig. 8 Histogram azimuth estimation

結合MUSIC算法用直方圖法計算出方位角為46°（入射角45°），定向精度在5°以內，說明小波降噪對保留信號的有用信息可取。

5 結 語

本文對多個頻率的信號進行多次仿真處理，研究顯示：小波降噪比傅里葉變換的處理效果更好，能得到更高的信噪比，更好保留信號的有用部分，并通過外場試驗數據進行驗證，得到很好的降噪結果，對方位的估計更準確。整體研究的復雜之處在于閾值的選取，降噪閾值過大或過小都會影響最終的降噪效果，閾值過大會造成細節部分丟失，過小則得不到最好的降噪效果。在此基礎上，還需要進一步研究，對現有方法進行改進或找出其他適合水聲信號的降噪方法，達到最完美的降噪效果。由于水聲環境的復雜性和可變性，對水聲信號的處理與學習還需要更加充分的學習，同時矢量陣在復雜海況下的各項性能還有待進一步提高完善，仍有很多工作需要完成，本文的研究工作可能有助于該技術的深入研究和發展，推動更廣泛的工程化應用。

[1]R. J. 尤立克. 水聲原理[M]. 哈爾濱: 哈爾濱工程大學出版社,1990: 67–75.

[2]李啟虎. 進入21世紀的聲納技術[J]. 應用聲學, 2002, 21(1):13–18.

[3]楊德森, 洪連進. 矢量水聽器原理及應用引論[M]. 北京: 科學出版社, 2009.

[4]彭玉華. 小波變換與工程應用[M]. 北京: 科學出版社, 1999.

[5]陳尚. 硅微仿生矢量水聲傳感器研究[D]. 太原: 中北大學,2007.

[6]姚直象, 惠俊英, 蔡平, 等. 單矢量水聽器方位估計的柱狀圖方法[J]. 應用聲學, 2006, 25(3): 161–167.

[7]徐明遠, 劉增力. MATLAB仿真在信號處理中的應用[M].西安: 電子科技大學出版社, 2007: 313–316.

[8]王拴中, 朱玉田. 改進小波閾值去噪法的對比性仿真實驗與分析[J]. 噪聲與振動控制. 2012, 32(1): 128-132.

[9]孫延奎. 小波分析及其應用[M]. 北京: 機械工業出版社,2005: 224–236.

[10]李芬. 矢量水聽器確定聲源目標方位估計研究[D]. 哈爾濱:哈爾濱工程大學, 2004.