基于北斗衛星速度外推的GEO衛星速度解算方法

，，，

(北京自動化控制設備研究所，北京 100074)

0 引言

北斗二代衛星導航系統是我國自主研發、建設、維護的衛星導航系統[1]，目前可以滿足亞太地區的定位需求，對于我國的國防安全、信息安全與導航產業發展有著重要的意義[2]。北斗二代系統為區域系統，一期導航星座于2011年12月開始試運行[3]。截至2017年6月底，北斗二代導航系統已經具備了7顆地球靜止軌道(GEO)衛星、8顆傾斜地球同步軌道(IGSO)衛星和7顆中軌道(MEO)衛星在軌正常運行、工作。為了利用有限的資源來滿足亞太地區導航與定位的需求，北斗二代導航系統利用GEO衛星來保證亞太地區實時有5顆可用星，保證了北斗系統在中國的重點范圍內能夠應用，而且隨著發射的衛星越來越多，GEO衛星可以提高在重點區域的定位、定速精度，在實際應用中有著重要意義。由于GEO衛星軌道傾角接近于0°，經典GPS廣播星歷參數中部分參數定義存在奇異，因此導致經典GPS廣播星歷參數擬合算法擬合精度降低[4]。杜蘭[5]等學者基于第一類無奇點根數，分析了無旋轉傾角的GEO兩步法星歷參數擬合算法，采用固定1～2個超限參數取值的縮減參數擬合法，取得了較好結果，但在某些時期擬合的用戶距離誤差較大。而現有北斗系統對其廣播星歷參數用戶算法進行了修正，即將GEO衛星軌道坐標旋轉5°。從而在經典廣播星歷參數用戶算法的基礎上提高了GEO衛星軌道的擬合精度。但這樣傳統的用戶衛星位置計算方法不再適用于GEO衛星，需要考慮5°的人為轉角[9]。文獻[6]利用Chebyshev多項式擬合算法計算GEO衛星位置，但在擬合時間越過星歷更新時刻時，需要多組星歷，增加了計算負擔，并且沒有涉及衛星速度計算。文獻[7]采用第二類無奇點軌道根數，避免了北斗GEO用戶算法中坐標旋轉處理過程，但長時間擬合位置和速度精度有所損失。文獻[8]提出了一種基于衛星位置差分的GEO衛星速度解算方法,但該方法在GEO衛星變軌時運算精度較低，無法滿足高精度的導航應用需求。文獻[10]給出了GEO衛星的速度微分計算方法，但該方法增加了矩陣微分運算，因此運算量較大。為此，本文首先推導了GEO衛星速度的位置差分解算方法和微分解算方法，并對兩種計算速度的方法做了對比，分析了兩種方法的優缺點，最后提出了基于加速度補償的GEO衛星速度外推算法。仿真結果表明：該算法在保證GEO衛星速度解算效率的前提下，提高了GEO衛星在各種復雜運動狀態下的速度解算精度，具有較高的工程實踐應用價值。

1 GEO衛星速度解算方法

北斗系統中GEO衛星保證了在中國區域內始終有5顆以上的可用星，地位十分重要。對其速度的解算精度也直接關系到使用者的定速精度，現一般有兩種方法解算其速度。

1.1 GEO衛星速度的位置差分法

由于GEO衛星在大部分時刻運動速度較低且運動加速度較小，因此可以采用位置微分運算的方法，該方法的計算如下所示。

(1)

其中，Xk-1、Yk-1、Zk-1是上一時刻所計算出的衛星位置，Δt是兩時刻之間的時間間隔。該方法的優點是運算量較低，但是該方法計算出的是衛星在2個定位時刻之間的平均速度，若是衛星加速度較大，則會引入較大的誤差。

1.2 GEO衛星速度的位置微分算法

由于北斗ICD中給出了GEO衛星軌道參數的微分量，因此可以采用微分法對GEO衛星的速度進行計算。

首先計算GEO的位置如式(2)所示[11]

(2)

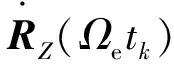
(3)

(4)

1)計算觀測歷元的偏近點角變化率

(5)

(6)

2)計算緯度幅角變化率

(7)

(8)

(9)

(10)

4)計算慣性系下衛星升交點經度變化率

(11)

5)計算衛星在自定義旋轉坐標系中的速度

(12)

(13)

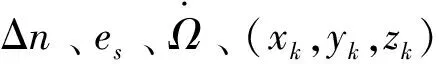
2 兩種速度解算方法的對比

衛星定速時需要實時地解算衛星速度，而位置微分算法相較于位置差分算法來說更為準確，它可以解算出定位時刻所需的衛星速度，而位置差分算法解出的卻是兩定位時刻之間的平均速度，在衛星速度較大時，會給定速帶來誤差。

利用2017年3月3日的renix文件中的北斗星歷，在北斗時間2017年3月2日23點—2017年3月3日23點，分別對兩種方法計算的GEO衛星速度進行仿真，其中衛星位置差分的時間間隔為1s，以微分法解出的GEO速度為基準計算位置差分法的誤差，結果如圖1所示。

(a)地固系X向速度誤差(a) Satellites velocity error of X axis in ECEF

(b) 地固系Y向速度誤差(b) Satellites velocity error of Y axis in ECEF

(c) 地固系Z向速度誤差(c) Satellites velocity error of Z axis in ECEF圖1 1號GEO衛星在地固系中速度誤差Fig.1 The error of PRN 1 GEO satellites velocity in ECEF

從圖1可知，在X、Y方向(ECEF系)上速度誤差較小，因為GEO衛星為同步衛星，在這2個方向上的速度分量小，加速度小；Z方向誤差雖然可以達到其他兩方向誤差的10倍，但量級依舊很小，最大只有約3mm/s的速度誤差，遠小于噪聲對定速造成的誤差，所以不會對定速造成影響。

表1 兩種算法時間對比

由以上仿真可知當GEO不存在大的機動時，利用位置差分法得到的GEO衛星速度完全可以滿足接收機定速的精度要求，同時該方法可以大幅降低GEO衛星的速度解算時間，降低北斗衛星導航系統的實現難度。

但是該方法的應用前提是GEO衛星軌道不存在軌道機動。軌道機動是指偏離預定軌道的衛星在發動機推力的作用下調整軌道使衛星返回到正確位置的工作[13]。軌道機動后，衛星位置變化可達數十km。其中的GEO和IGSO衛星由于其地球同步性，軌道機動比較頻繁[14]。但是當GEO衛星機動發生，軌道預報將很快失效，一直到機動結束后較長時間內星歷都不能有效使用，為此有眾多學者研究了衛星機動期間定軌方法和機動后星歷快速恢復方法，使得衛星機動期間的軌道參數精度可以接受[15]。為模擬其軌道的機動，選取一顆MEO衛星進行對GEO衛星軌道機動時的仿真，其結果如圖2所示。

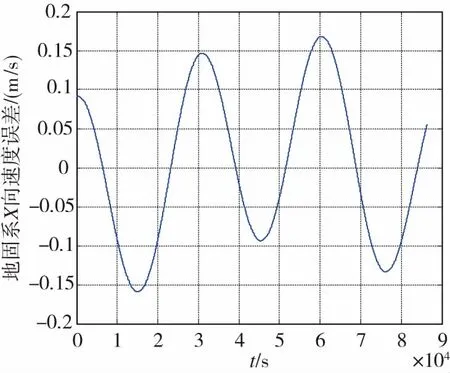
(a) 軌道機動時地固系X向速度誤差(a) Satellites velocity error of X axis in ECEFduring orbital maneuver

(b) 軌道機動時地固系Y向速度誤差(b) Satellites velocity error of Y axis in ECEFduring orbital maneuver

(c) 軌道機動時地固系Z向速度誤差(c) Satellites velocity error of Z axis in ECEFduring orbital maneuver圖2 GEO衛星軌道機動時在地固系中速度誤差Fig.2 The error of GEO satellites velocityduring orbital maneuver in ECEF

在軌道機動時差分算法會帶來很大的衛星速度計算誤差。其誤差大小主要與機動時衛星的加速度大小有關。當衛星調整軌道時往往通過其內部提供推力，產生較大加速度，在較短時間內完成軌道調整。加速度與誤差關系如圖3所示。

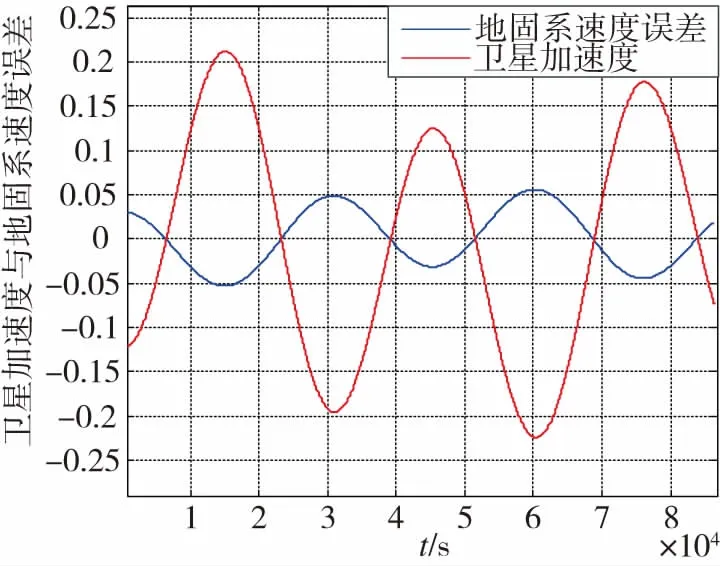
圖3 衛星加速度與速度誤差Fig.3 Satellites acceleration and velocity error

當不考慮任何測量誤差的情況下，地固系中的速度誤差將直接引入到接收機所測量的偽距率中，并按視線系和地理坐標系之間的角度關系分配到接收機所輸出的速度中，導致接收機的定速有一定偏差，不利于導航系統精度的提高。因此需要對這種方法進行改善。

3 基于速度外推的GEO衛星速度計算方法

由之前的分析可知，利用位置差分法雖然可以降低GEO衛星速度計算的運算量，但是若GEO衛星存在較大的變軌機動時，則現有的位置差分法計算得到的GEO衛星速度誤差較大，會影響接收機的定位精度，為了在保證GEO衛星速度計算運算量的前提下進一步提高北斗衛星導航接收機的定速精度，本文提出了一種基于接收機速度外推的GEO定速方法。

若已知衛星的加速度，則可對衛星速度進行補償。一種簡單的補償思想為視時間間隔內的衛星加速度不變，則位置差分算法計算的衛星速度實際上是2個時刻中間時的瞬時速度，可以用式(14)進行補償，以減小速度延時造成的誤差，滿足高精度緊組合導航系統的應用需求。

(14)

其中，Vxdk、Vydk、Vzdk分別為位置差分算法所計算的衛星在地固系中的速度，axdk、aydk、azdk分別為位置差分算法所計算的衛星在地固系中的加速度，Vxk、Vyk、Vzk為補償后的衛星速度，利用式(2)對時間求導計算衛星在地固系中的加速度。

(15)

(16)

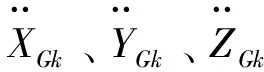
(17)

其中，Vxdk -1、Vydk -1、Vzdk -1是上一周期位置差分所計算的衛星速度。為驗證此種方法的可行性，在機動條件下將兩種方法得到的加速度做差對比，其結果如圖4所示，誤差基本在10-7量級，所以用式(17)計算完全可以滿足使用需求。

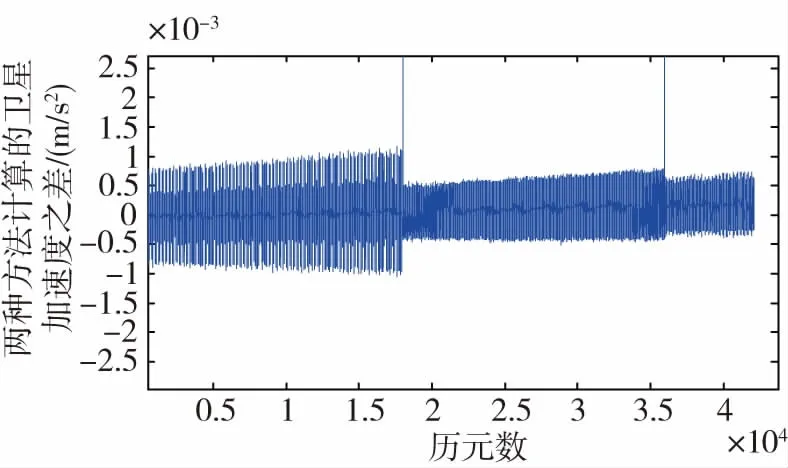
圖4 兩種方法計算衛星加速度之差Fig.4 The difference of satellites accelerationcomputed by two methods

除式(14)外，還可以用多項式擬合法、引入加加速度法等對誤差進行補償，以上方法對誤差補償有一定改進效果，但由于加加速度較小而且衛星機動的不確定性，有時也會產生更大誤差，本文僅討論式(14)的補償方法。

4 仿真分析

利用上述算法對第2節中軌道機動時的GEO衛星速度差分算法進行補償，仿真結果如圖5所示。

(a) 補償后軌道機動時地固系X向速度誤差(a) Satellites velocity error of X axis in ECEF aftercompensating during orbital maneuver

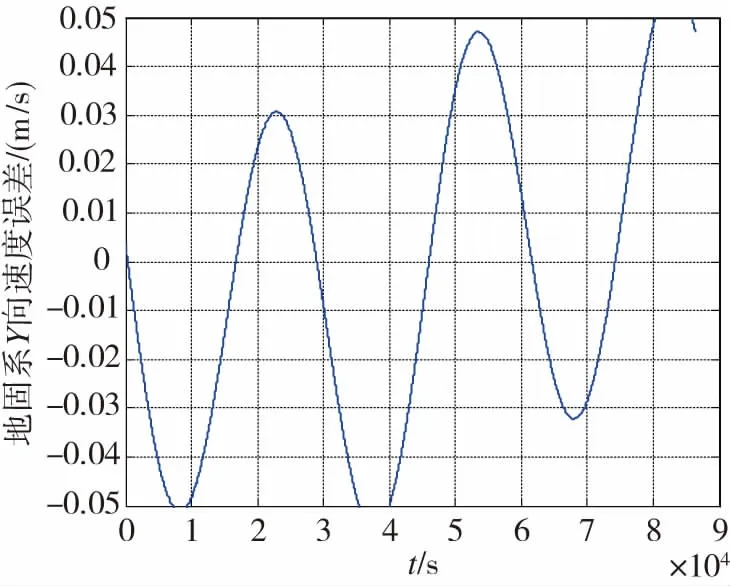
(b) 補償后軌道機動時地固系Y向速度誤差(b) Satellites velocity error of Y axis in ECEF aftercompensating during orbital maneuver

(c) 補償后軌道機動時地固系Z向速度誤差(c) Satellites velocity error of Z axis in ECEF aftercompensating during orbital maneuver圖5 補償后的軌道機動GEO衛星在地固系中速度誤差Fig.5 GEO satellites velocity error during orbitalmaneuver after compensating in ECEF

對比圖2，圖5中的速度誤差縮小到近1/4，尤其較好地補償了Z方向上的誤差，證明了加速度補償速度外推算法的有效性。

表2 差分法和速度外推法時間對比

兩種算法執行效率相當，而補償后的精度卻可以提升約4倍以上，仿真結果證明了此算法的優越性。

由于目前接收機的輸出頻率通常為5Hz，所以將接收機輸出的步長減小為0.2s時，使用差分法得到的軌道機動時GEO衛星速度誤差如圖6所示。

當接收機輸出的時間間隔為0.2s時，利用速度外推法補償后的速度誤差如圖7所示。

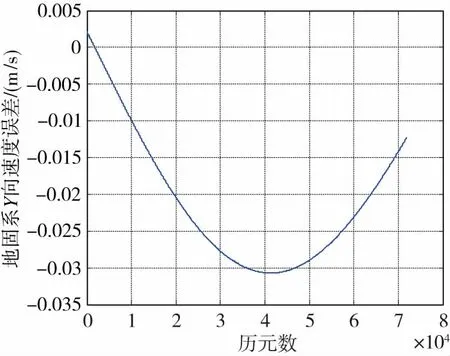
(b)軌道機動時地固系Y向速度誤差(時間間隔0.2s)(b) Satellites velocity error of Y axis in ECEFduring orbital maneuver (time interval 0.2s)

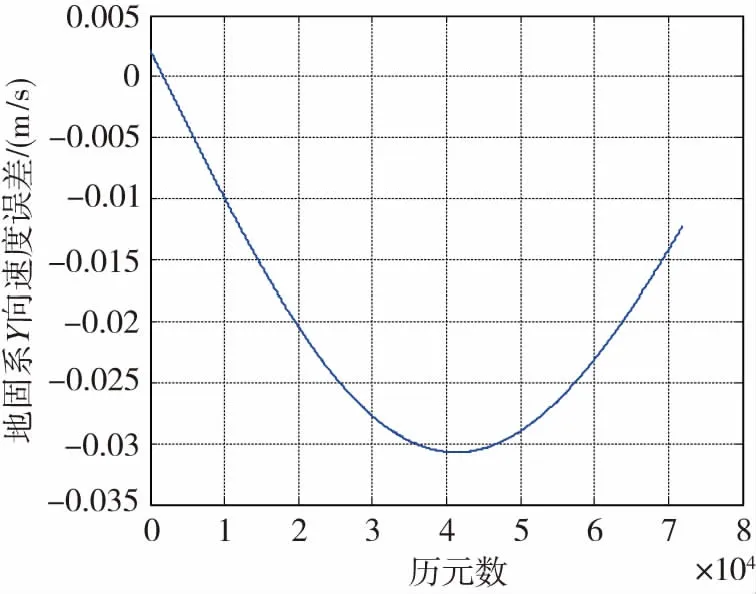
(c)軌道機動時地固系Z向速度誤差(時間間隔0.2s)(c) Satellites velocity error of Z axis in ECEFduring orbital maneuver (time interval 0.2s)圖6 GEO衛星軌道機動時在地固系中速度誤差(時間間隔0.2s)Fig.6 The error of GEO satellites velocity during orbitalmaneuver in ECEF(time interval 0.2s)

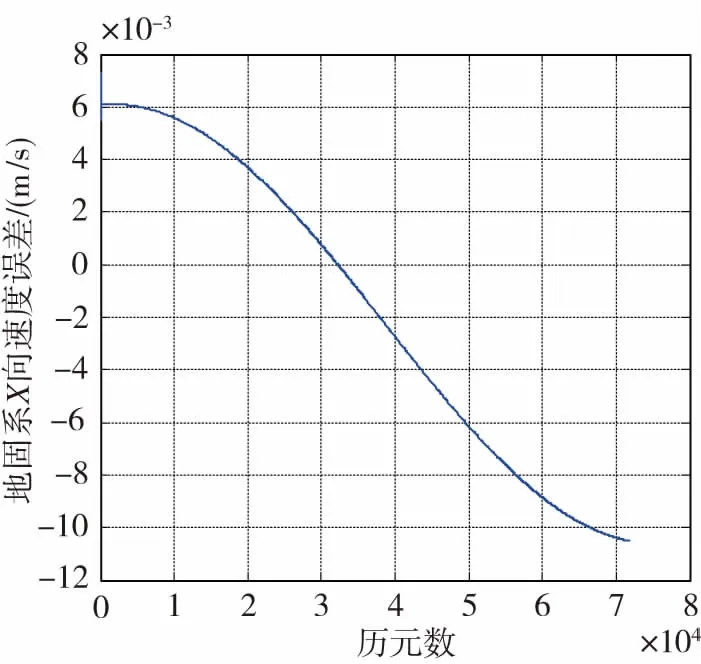
(a) 補償后軌道機動時地固系X向速度誤差(時間間隔0.2s)(a) Satellites velocity error of X axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)

(b) 補償后軌道機動時地固系Y向速度誤差(時間間隔0.2s)(b) Satellites velocity error of Y axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)

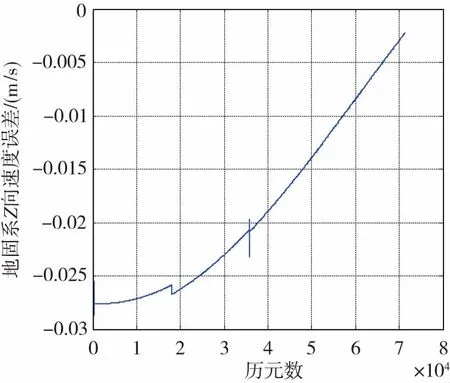
(c) 補償后軌道機動時地固系Z向速度誤差(時間間隔0.2s)(c) Satellites velocity error of Z axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)圖7 補償后的軌道機動GEO衛星在地固系中速度誤差(時間間隔0.2s)Fig.7 GEO satellites velocity error during orbital maneuverafter compensating in ECEF (time interval 0.2s)

由圖7可以看出，衛星位置之間的時間間隔越小，衛星速度越準確，相應的定速精度也就越高。而經過補償的速度誤差也達到了毫米量級，能夠滿足應用需求。

由以上仿真結果可知：本文提出的基于速度外推的GEO衛星速度計算方法在保證GEO衛星速度解算速度的前提下，提高了GEO衛星在各種復雜運動狀態下的速度解算精度。

5 結論

針對現有北斗GEO衛星速度解算方法存在的缺陷，為了提高北斗衛星導航系統在各種復雜環境下的導航精度，本文在已有的GEO衛星速度解算方法的基礎上提出了一種基于速度外推的GEO衛星速度計算方法，仿真結果表明：該算法在保證GEO衛星速度解算速度的前提下，提高了GEO衛星在各種復雜運動狀態下的速度解算精度，具有較高的工程實踐應用價值，可以有效地提高北斗衛星導航系統的應用效果。

[1] 楊秋實, 徐愛功, 祝會忠,等. BDS單參考站載波相位差分定位方法[J]. 導航定位學報, 2016, 4(4):59-64.

[2] 鮑宇. 北斗導航系統的建設與應用分析[J]. 電子制作, 2013(16):15.

[3] 中國衛星導航系統管理辦公室.中國北斗衛星導航系統[R]. 2016.

[4] 劉季. 北斗GEO衛星位置計算方法探究[J]. 測繪地理信息,2012,37(5):33-36.

[5] 杜蘭, 劉澤軍, 周佩元,等. 無旋轉傾角的NAV/CNAV型GEO廣播星歷擬合[J]. 測繪學報, 2017, 46(3):297-306.

[6] 歐美極. 北斗衛星導航系統的Chebyshev多項式擬合算法[J]. 中國科技信息, 2015(19):83-84.

[7] 謝小剛, 曾大治, 龍騰,等. 北斗GEO衛星用戶算法的改進方法[J]. 國防科技大學學報, 2014,36(1):82-87.

[8] 劉廣軍, 郭晶, 羅海英,等. 北斗GEO衛星實時求速算法研究[J]. 飛行器測控學報, 2015, 34(1):57-63.

[9] Jia S, Tang X, Xiao Z, et al. Analysis of The GEO multipath impact on Ionosphere-Free Combination Positioning in BDS system[C]// 2016 IEEE International Conference on Signal Processing, Communications and Computing(ICSPCC). IEEE, 2016:1-4.

[10] 黃勇, 胡小工, 王小亞,等. 中高軌衛星廣播星歷精度分析[J]. 天文學進展, 2006, 24(1):81-88.

[11] 中國衛星導航系統管理辦公室.北斗衛星導航系統空間信號接口控制文件[R]. 2016.

[12] Guangjun，Jing Guo. Real-time Determination of a BDS Satellite’s Velocity Using the Broadcast Ephemeris[C]//2014 4thInternational Conference on Instrumentation and Measurement, Computer, Communications and Control. 2014:478-463.

[13] 楊旭海, 李志剛, 馮初剛,等. GEO衛星機動后的星歷快速恢復方法[J]. 中國科學:物理學 力學 天文學, 2008, 38(12):1759-1765.

[14] 燕興元, 黃觀文, 張睿,等. 一種基于廣播星歷的 BDS 軌道機動探測方法[J]. 導航定位學報, 2015,3(3):35-38.

[15] 郭睿, 李曉杰, 周建華,等. 機動力建模條件下的GEO衛星機動期間定軌[J]. 測繪科學技術學報, 2013, 30(5):465-470.

[16] 謝鋼. GPS原理與接收機設計[M]. 北京：電子工業出版社, 2009:62-66.