吊放聲吶絞車吊纜振動分析
張同喜 龔方友
中國船舶重工集團公司第715研究所,杭州,310000
0 引言
航空絞車在軍用領域應用廣泛,是吊放聲吶探測系統的重要組成部分,主要用于航空聲吶的吊放和回收,其操作簡單,自動化程度高。由于反潛直升機處于海洋環境中,在惡劣的海況下,機身擺動較為劇烈,這不僅會降低聲吶的投放精度,還會導致吊放電纜及聲吶設備的損傷[1],因此對航空聲吶吊放系統進行振動分析,對航空絞車的作業有積極作用。
航空絞車吊放系統包括吊頭、吊纜、吊物(聲吶),在機身和風速等影響下,吊纜和吊物的運動包含有復雜的非線性現象[2]。為了便于分析絞車吊放系統的運動規律,從而描述出絞車作業時吊纜的實時運動形態,可以將其運動分解為吊物的擺動以及吊纜受激勵下的振動。吊物擺動可以分為單擺模型[3-4]和空間球擺模型[5]。CHIN等[6]用彈性球擺來模擬吊重,對懸掛吊重的擺動進行了分析;HENRY等[7]建立了一個集中質點組成的平面單擺模型,對吊重的擺動進行分析;董秋艷等[8]對起重船吊物系統的動力學響應進行了研究;胡于進等[9]對運架梁起重船吊重擺動進行了分析。目前一些文獻都是對吊物在不同工況下的擺動進行分析研究,少有涉及其振動的研究。
本文以某型航空絞車為研究對象,基于以球坐標為擺動角的單擺理論,建立聲吶擺動數學模型,推導出絞車收放作業時吊放電纜的振動微分方程。通過數值方法分析了不同的激勵頻率對吊物擺動的影響,并且對吊纜振動情況做了研究,從而對聲吶擺動過大的情況進行預測,能有效地避免作業中吊放系統和聲吶設備的損傷。
1 機身激勵下吊纜運動分析
1.1 絞車吊放系統坐標系轉換
根據絞車吊放系統吊纜運動特性,在水平面內建立絕對坐標系oxyz,如圖1所示,其中,x軸指向機身頭部,y軸指向翼弦,z軸垂直向下。
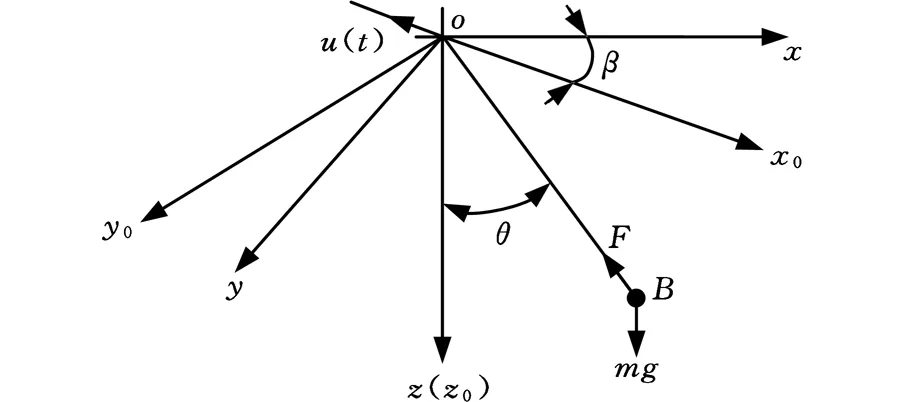
圖1 吊放系統結構示意圖Fig.1 Shematic of lifting system
隨機身運動的坐標系為相對坐標系ox0y0z0,當吊頭在平面內運動時,ox與ox0夾角為β,絞車吊放系統中吊頭的絕對坐標(x,y,z)與相對坐標(x0,y0,z0)之間轉換關系為
x=x0cosβ-y0sinβ
y=x0sinβ+y0cosβ
z=z0
1.2 吊纜擺動數學模型
從上述分析可知,機身對吊頭的影響體現在x、y、z三個方向位移的變化,因此選取一個方向分析即可,為便于分析,在這里選取吊頭x軸方向的位移u(t)來分析吊物擺動情況。設聲吶質量為ms,吊纜長度為L,假定吊頭在x軸位移變化為簡諧運動,則t時刻吊頭位移為
u(t)=Ucosωt
(1)
式中,U為吊頭運動最大位移;ω為吊頭激勵頻率。
根據單擺原理[10],可得到吊物的擺動方程:
(2)
式中,c為阻尼系數,c=0.05;ωn為系統固有頻率;θ為吊物擺角。
聯立式(1),可以得到式(2)的解析解:
θ=Acos(ωt+β)
(3)
式中,A為擺角幅值。
根據吊纜方向受力可得吊纜張力
1.3 吊纜振動微分方程
由吊纜材料特性可知,吊纜不能承受彎矩,即抗彎剛度為0,吊放系統吊纜振動如圖2所示。
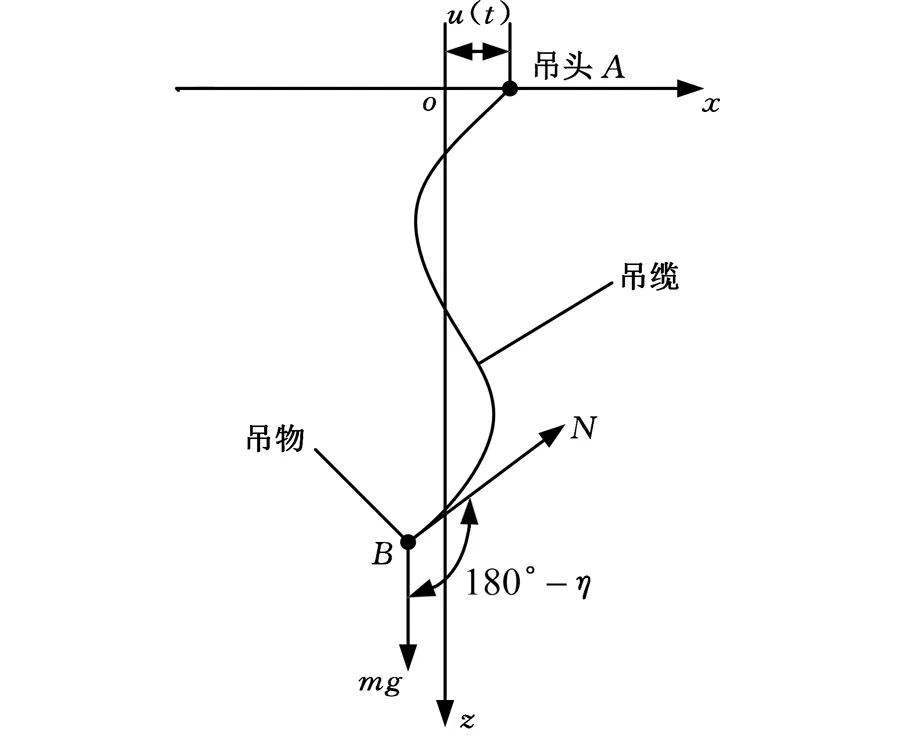
圖2 吊纜的振動分析Fig.2 Vibration analysis of suspended cable
設吊纜單位長度質量為w,吊纜張力為N,吊纜各節點橫向振動位移為x(z,t),吊纜單位長度所受風載荷為q(z,t),可以利用哈密頓原理[11-12]推導出吊纜橫向振動非齊次微分方程:
(4)
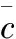
根據吊放系統運動特性,確定以下初始邊界條件:
(1)初始條件
(5)
(2)邊界條件
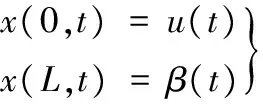
(6)
其中,u(t)表示吊頭激勵x方向位移,由機身振動情況而定。
由圖2,對吊物進行受力分析可得:
(7)
由于η值較小,因此可得?x/?z=-tanη,cosη=1,那么式(7)可以化為
(8)
結合式(4),根據單擺運動分析,可以得到式(8)的解析解:
x(z,t)=Uexp[ω2(z-BL)/g]sinωt
(9)
式中,B為控制吊物擺動幅度的參數,B=2。
z=L時,式(9)可化為
x(L,t)=Uexp(-ω2L/g)sinωt
(10)
根據式(10)可以得到式(4)的邊界條件。
2 吊纜振動微分方程數值算法
為了滿足吊纜振動的實時性,在吊纜微分方程滿足初始條件(式(5))和邊界條件(式(6))時,采用顯式差分法[13-14]來求解式(4),可得吊纜實時的運動形態。在運用差分方法求解偏微分方程時,先要將連續問題離散化,在求解區間劃分網格,網格劃分如圖3所示。
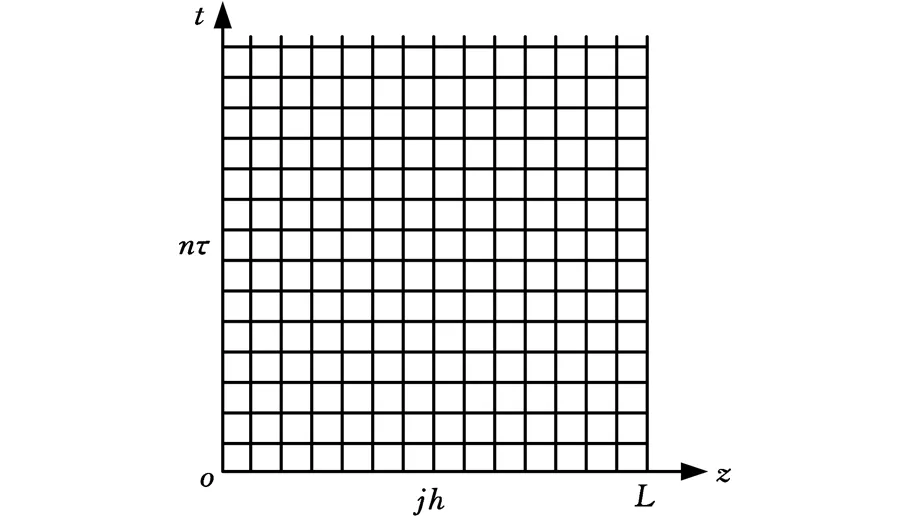
圖3 z-t網格劃分Fig.3 z-t mesh division
由圖3可以看出,方程的求解區間為
R={(z,t)|0
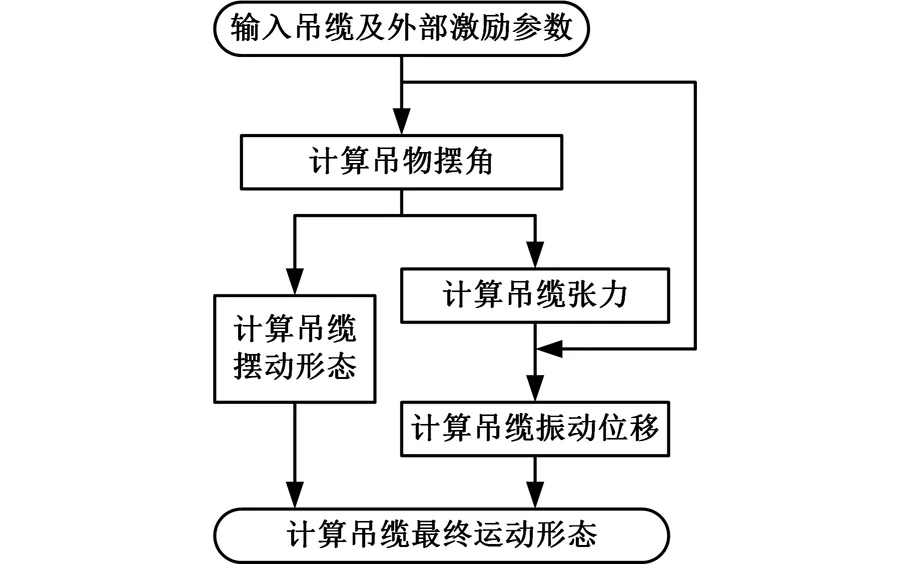
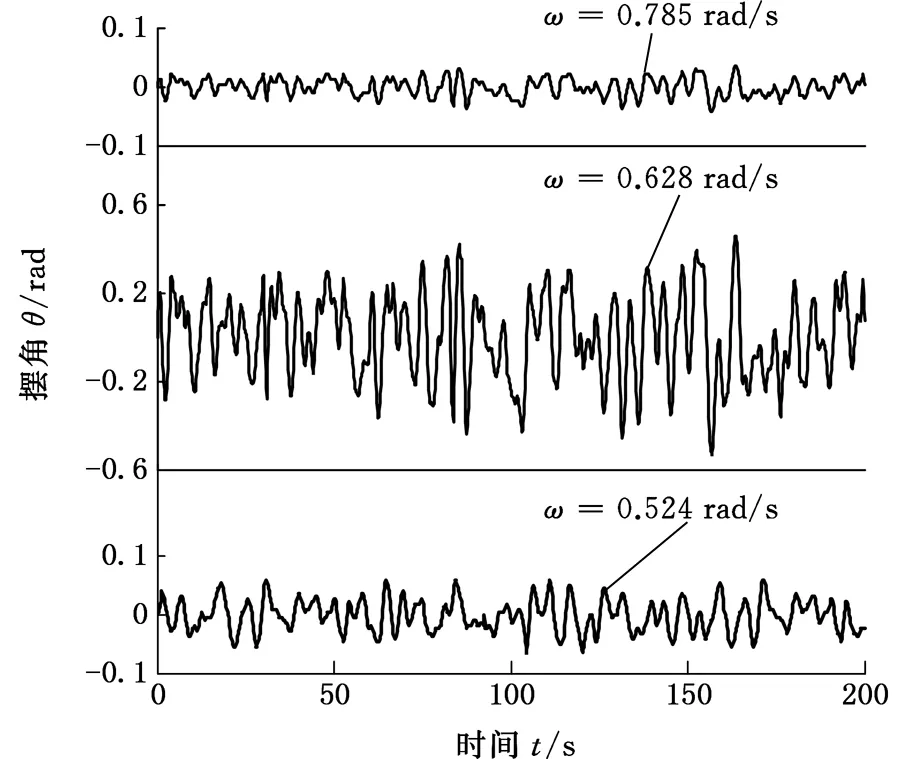
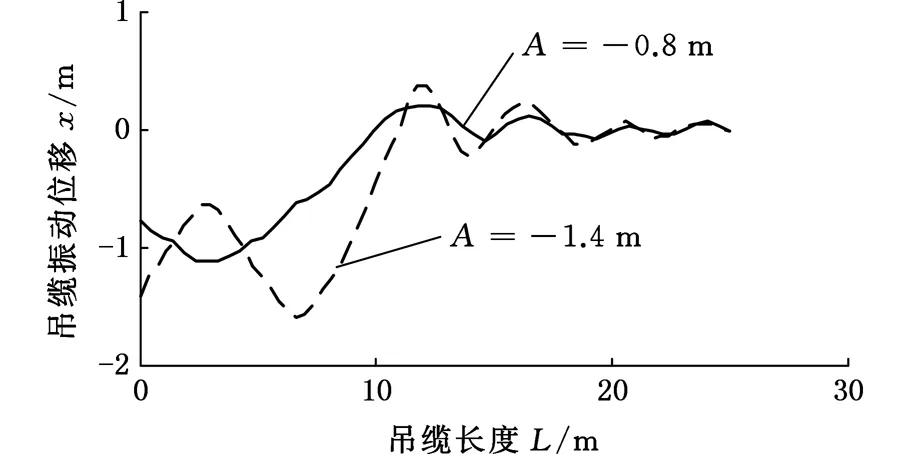
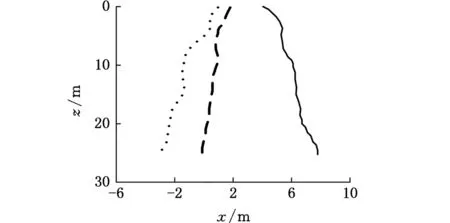
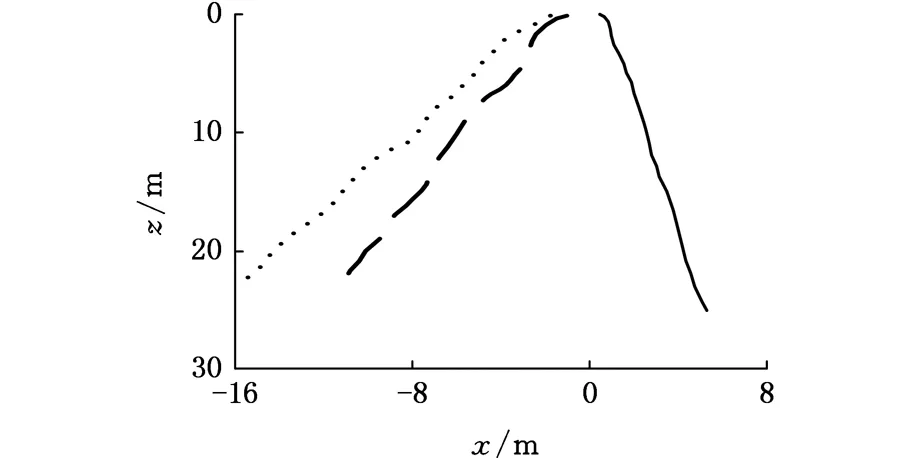
在這里,首先將求解區間0 zj=jhj=0,1,…,m tn=nτn=0,1,…,T 式中,h為空間步長,h=L/m;τ為時間步長。 將式(4)差分化并整理,可以得到控制方程的差分格式: (11) a1=a5=-N/h2,a2=2N/h2-2w/τ2,a3= a4=w/τ2 離散化式(5)和式(6)并整理可以得到 (12) (13) 結合式(12)、式(13),由式(11)就可以依次迭代出x(z,t)在每個網格點的數值。吊纜形態實時仿真計算過程如圖4所示。 圖4 吊纜形態實時仿真計算過程Fig.4 Flow chart of the cable real-time simulation 為了驗證本文理論分析及數值解算方法的準確性,設置吊頭為正弦激勵輸入情況下,吊頭在x軸方向位移幅值u(t)=1.8 m,算例中吊纜長度為24.85 m(系統固有頻率為0.628 rad/s),吊纜直徑9 mm,吊纜線密度為0.1 kg/m,聲吶質量ms為68 kg,風速為10 m/s;仿真空間步長h=L/50,時間步長τ=0.5 s。為便于分析,提供作業過程中的三種不同激勵頻率。 針對仿真算例,首先分析不同激勵頻率下,吊放系統響應情況,在此情況下不考慮吊纜的升降,不同激勵頻率時,200 s內吊纜擺角的變化如圖5所示,可以看出,隨著激勵頻率的減小,吊纜的擺角逐漸變大,當激勵頻率達到系統固有頻率附近時,最大擺角約為26°,這是由于激勵頻率接近吊放系統固有頻率引起系統共振,而當激勵頻率繼續減小時,吊纜擺角逐漸減小。 圖5 吊纜擺角響應曲線Fig.5 Swing angle response curve of cable 為了分析吊頭激勵位移對吊纜振動的影響,進行了兩種不同吊頭激勵位移下吊纜振動仿真測試。吊頭激勵位移A分別為-0.8 m和-1.4 m時,吊纜振動響應如圖6所示。由圖6可以看出,吊纜在靠近吊頭附近范圍內,振動是最劇烈的。在相同激勵頻率下,吊頭位移越大,吊纜振動越大,并且沿著吊纜方向振動逐漸減小;在激勵頻率接近系統固有頻率時,相同的吊頭激勵位移下,吊纜振動有所增加,但不是很明顯,說明系統發生共振的情況下對吊纜振動有一定加強。 (a)ω=0.785 rad/s (b)ω=0.628 rad/s圖6 吊纜橫向振動位移Fig.6 Transverse vibration displacement of cable 為了更直觀地了解吊纜的擺動情況,根據線性疊加原理,將吊物的擺動與吊纜的振動進行疊加,得到的吊纜形態如圖7所示。激勵頻率為0.785 rad/s、0.628 rad/s時,對吊纜最終擺動形態進行描述,為了分析吊纜擺動形態隨時間變化,每幅圖顯示了3個不同時刻吊纜的形態,其中最左側點線代表最后時刻電纜擺動形態,其余部分代表最后時刻之前電纜擺動形態。 (a)ω=0.785 rad/s (b)ω=0.628 rad/s圖7 吊纜擺動形態仿真結果Fig.7 Simulation results of cable swing 通過仿真結果可知,吊纜擺動形態自然,數值方法解算結果準確、收斂性好,適用于航空吊放聲吶絞車作業時聲吶擺動的預測與控制。 (1)機身對吊頭的激勵對吊放系統的擺動影響是非常明顯的,當激勵頻率達到吊放系統固有頻率時,聲吶的擺動角度到達最大,因此在作業中應該盡量避免發生這種情況。 (2)通過改變吊頭橫向激勵位移可以改變吊纜振動劇烈程度,橫向激勵越大,吊纜振動越劇烈;當外部激勵頻率接近系統固有頻率時,吊纜振動程度有所增加。 (3)本文采用的顯式差分法有效地應用于本文建立的數學模型,仿真結果表明,本文理論分析的準確性高、數值方法收斂性好。 [1] 王成, 傅安. 液壓絞車改善被吊物體動態狀態的控制方法[J].火力與指揮控制, 2015, 40(9): 163-166. WANG Cheng, FU An. Control Methods of Improve Dynamic State of Subjects Hanged on Hydraulic Winch[J] Fire Control & Command Control, 2015, 40(9): 163-166. [2] 任會禮, 王學林, 胡于進, 等. 起重船吊物系統動力響應仿真分析[J]. 系統仿真學報, 2007, 19(12): 2665-2668. REN Huili, WANG Xuelin, HU Yujin, et al. Dynamic Response Simulation of Lifting Load System of Ship-mounted Cranes[J]. Journal of System Simulation, 2007, 19(12): 2665-2668. [3] 陳志梅, 孟文俊. 龍門起重機的模糊滑模定位與防擺控制[J]. 中國機械工程, 2012, 23(3): 310-314. CHEN Zhimei, MENG Wenjun. Fuzzy Sliding Mode Positioning and Anti-swing for Gantry Crane[J]. China Mechanical Engineering, 2012, 23(3): 310-314. [4] KUO A D. The Six Determinants of Gait and the Inverted Pendulum Analogy: a Dynamic Walking Perspective[J]. Human Movement Science, 2007, 26(4):617-56. [5] YAZID E, PARMAN S, FUAD K. Vibration Analysis of Flexible Gantry Crane System Subjected Swinging Motion of Payload[J]. Journal of Applied Sciences, 2011(11): 1707-1715. [6] CHIN C M, NAYFEH A H. Dynamics and Control of Ship-Mounted Cranes[J]. Journal of Vibration and Control, 2001,7(6): 891-904. [7] HENRY R J, MASOUD Z N, NAYFEH A H, et al. Cargo Pendulation Reduction on Ship-mounted Cranes via Boom-luff Angle Actuation[J]. Journal of Vibration and Control, 2001, 7(8): 1253-1264. [8] 董艷秋, 韓光. 起重船吊物系統在波浪中的動力響應[J]. 中國造船, 1993 (1): 63-71. DONG Yanqiu, HAN Guang. Dynamic Response of Lifting Load System of Crane Vessel in Waves[J]. Shipbuilding of China, 1993 (1): 63-71. [9] 胡于進, 文定旭, 王學林. 運架梁起重船吊重擺動分析[J]. 系統仿真學報, 2012, 24(7): 1501-1509. HU Yujin, WEN Dingxu, WANG Xuelin. Swing Analysis of Suspended Load System for Crane Ship of Transporting and Lifting Girders[J]. Journal of System Simulation, 2012, 24(7): 1501-1509. [10] 高順德, 楊超, 滕儒民,等. 全地面起重機塔臂工況吊重擺振特性研究[J]. 中國工程機械學報, 2013, 11(4): 303-308. GAO Shunde, YANG Chao, TENG Ruming, et al. Research on Swing and Vibration Characteristics of Tower Crane in All Terrain Crane[J]. Journal of Mechanical Engineering China, 2013, 11(4):303-308. [11] LIU Y J, TANG K, JONEJA A. Modeling Dynamic Developable Meshes by the Hamilton Principle[J]. Computer-Aided Design, 2007, 39(9):719-731. [12] 黃建亮, 陳樹輝. 縱向與橫向振動耦合作用下軸向運動梁的非線性振動研究[J]. 振動與沖擊, 2011, 30(8): 24-27. HUANG Jianliang, CHEN Shuhui. Study on Nonlinear Vibration of an Axially Moving Beam with Coupled Transverse and Longitudinal Motions[J]. Journal of Vibration and Shock, 2011, 30(8): 24-27. [13] 李榮華,劉播. 微分方程數值解法[M]. 北京:高等教育出版社, 2009. LI Ronghua, LIU Bo. Numerical Methods for Differential Equations[M]. Beijing: Higher Education Press,2009. [14] 王文, 錢江. 有限差分法模擬電梯懸掛系統橫向受迫振動[J]. 振動工程學報, 2014, 27(2): 180-185. WANG Wen, QIAN Jiang. Finite Difference Method for Simulating Transverse Forced-vibration of Elevator Suspended System[J]. Journal of Vibration Engineering, 2014, 27(2): 180-185.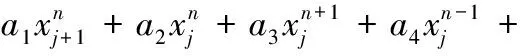
3 仿真算例及其結果分析
3.1 仿真作業算例
3.2 仿真結果分析

4 結論

