局部協同選擇聚類的多視角社區發現研究①

于 悅,盧 罡,郭俊霞

(北京化工大學 信息科學與工程學院,北京 100029)

1 引言

如今,隨著大量網絡應用平臺的產生,用戶會根據自身的不同特點(社會角色)來選擇不同的應用平臺并與他人進行交互和信息資源的共享,所以,同一個用戶可以在多種平臺上處于不同的關系網絡結構中,這樣的網絡結構也被稱為多維關系網絡,每個維度代表一種不同的關系視角[1],例如,不同學術期刊論文可以構建不同的作者協作網絡,在某些期刊中兩個同社團的作者(研究領域相同),在其他期刊中也認為應該在同一個社團;又如,兩個用戶在某些社交平臺是好友關系,在其他社交平臺中則認為這兩個用戶是好友的可能性很高,所以利用不同關系網絡的信息來發覺某個應用中隱藏的社團結構并進行有利的信息整合是現代信息挖掘的主要方向.

在傳統的單視角社區發現算法中,我們可以將人物關系整合到圖的拓撲結構中,用戶代表圖中的節點,邊表示用戶間的交互關系和關聯屬性,社區發現的過程被看作是圖聚類分析的過程,因此,基于圖劃分的單視角聚類算法被相繼提出,如K均值(K-means)算法[2]、譜聚類算法(Spectral Clustering)算法[3]、規范割集準則(Ncut)算法[4]、對稱非負矩陣因式分解(symNMF)算法[5,6]等.這些算法有明顯的兩個特點[7]:(1)切割式聚類,即節點被聚類到沒有交集的聚簇中;(2)簡單的圖形構造,即兩個節點之間最多只有一條代表關系的連邊.然而在很多實際應用中,表示社區結構的圖數據往往來自于不同的視角(領域),單視角的劃分和構造難以綜合考慮多種因素.例如,在現實生活中,企業需要尋求某個研究領域中的專家.根據論文作者之間的引用及合作關系可以得到社團劃分結果為R1=({A,B,C,D,G,K},{L,M,N,O,P,Q},{P});同時,根據項目合作和協助關系的社團劃分結果為R2=({A,C,D,E,F,P},{L,M,N,O,R},{Q}).可以看出,第一個視角不能將P進行有效的劃分,同理,第二個視角不能將Q進行有效劃分,所以,這種劃分結果考慮的用戶關系較為單一,很難有效解決這種多維關系網絡的問題.

針對以上這種同源異構的數據,近年來基于多視角聚類方法比較受關注,文獻[8,9]的算法都是圖切割原理結合不同的視角關系來定義的,它們根據切割聚簇內節點代價大、切割聚間節點代價小的原理,提出相應的目標函數公式,將離散問題轉換為連續問題,對其進行優化,求出函數收斂后所對應的聚類結果.這些算法的關鍵在于收斂條件的確定,而極值點和最值點不易確定.文獻[10]的CCA算法,是用其它視角的聚類結果來更新本視角下節點的初始狀態,用聯合訓練的方法,通過對拉普拉斯矩陣不斷的更新迭代來改善聚類精度.文獻[11]的CSC算法是對CCA的改進,利用拉普拉斯矩陣的特征向量對相似矩陣進行迭代更新,使矩陣中同屬一個聚簇的節點權值相近,簇間節點的權值不同,最后串聯個視角的特征向量進行融合,并用K-means算法聚類結果.文獻[12]的SCSC算法針對CSC算法進行改進,利用選擇投票的方式,對強視角(節點信息完全)和弱視角(顯示部分節點信息)做不同的選擇處理,最終實現多視角聚類.但該處理方法較簡單,主要針對多稀疏實例集的稀疏關系聚類,精度提升較差.文獻[12,13]都是使用正則化方法,使用基于拉普拉斯特征向量來調節缺失函數,這樣由每個拉普拉斯矩陣得出的聚簇結果在所有的視角中是一致的.這些算法假設前提為不同視角下的節點分布是相同的,假設條件比較苛刻.文獻[14]提出的CGC算法利用節點之間的關聯矩陣關系,對視角中不同的實例集進行一對多和多對多的處理,實現最后的聚類,然而該算法中選取關聯關系困難,沒有明確的公式定義.

傳統多視角聚類都有兩個限制:(1)每個視角下的節點關系不同,但每個視角要求使用相同的節點,且每個視角中的節點聚簇個數要求相同.(2)每個視角基本上必須擁有圖結構中的充分劃分信息.以上限制條件,導致這些方法往往不能反映真實的網絡結構,所以在實際應用中的適應性比較差.

本文針對傳統的單視角社區發現算法的局限性和現有的多關系社區發現算法的不足提出一個協同選擇聚類的多視角社區發現算法,并從多個方面對算法進行改進,本文主要貢獻點包括以下3個方面.

(1)使用局部協同訓練方法解決大多數多視角聚類算法中實例和聚簇條件的限制,允許不同視角中選擇不同數量的節點,每個視角的劃分數量也可以不同.

(2)解決傳統多視角算法中其他視角的決定性修正而導致聚類不準確的問題.本文只對各個視角中可識別節點(在其他視角中有關系)的聚類結果進行強促進處理和弱促進處理,迭代更新每個視角中識別節點關系的相似矩陣,促進各視角中部分結構的融合.

(3)將局部學習和聯合訓練相結合,利用每個視角中的不可識別節點(在其他視角中無關系)的鄰居節點劃分情況,來得到非標記節點的最終歸屬.

本文的結構分為以下幾個章節:第1節是對現有社區發現的介紹和新算法的提出;第2節提出多視角局部協同選擇聚類算法(co-MLSC)并介紹其原理;第3節介紹該算法中的核心公式;最后,通過實驗,驗證算法的有效性.

2 局部協同選擇多視角聚類算法

2.1 譜聚類

譜聚類[3](CS)方法是利用拉普拉斯矩陣特征向量的性質來挖掘社團方法,其定義為:設G= (V(G),E(G))是網絡圖結構,其中節點集為V(G)= {v1,v2,...vm},邊集為E(G).譜聚類的算法流程如算法1所示.

算法1.譜聚類(CS)輸入:相似矩陣S∈Rm×m,聚類個數k∈N輸出:該相似矩陣所代表的點的聚類結果C∑1.計算S的對角矩陣2.計算拉普拉斯矩陣L = D–S?3.計算L的前k個特征向量,4.正規化U矩陣的每一行5.樣例j屬于聚簇c當且僅當通過K-means算法得到U的j行屬于聚簇c6.計算并返回結果矩陣

聚類結果矩陣C表示聚類結果矩陣,其中第i行j列的元素表示視角中實體i與實體j是否在同一個聚簇中,在則為1,反之則為0.

2.2 co-MLSC算法

本節設計一種多視角協同選擇的聚類算法,該算法是基于多視角譜聚類算法的基礎上提出的.針對多視角聚類算法應用到實際網絡關系中的限制問題,該算法將每個視角中的實例分為兩種,當某個視角中的兩個節點在其他視角中存在并屬于同一社團結構,則這兩個節點在該視角中為可識別節點,反之,如果某一個節點在其他視角中不存在或存在但沒有對應的關系,則節點在該視角中為不可識別節點.所以,co-MLSC對實例的處理也分為兩種方法,其中包括多視角中可識別節點的強弱關系促進方法和各個單視角中不可識別節點的劃分方法,其流程如算法2所示.

算法2.協同式多視角選擇聚類算法(co-MLSC)輸入:各個view的相似度矩陣,各個view中聚類個數.輸出:最終聚類結果.1.Initialize:.2.用譜聚類CS算法得到各視角初始聚類結果矩陣,j∈d,3.for i = 1 to iter do //iter表示迭代次數4. for π = 0 to d–1 do 5. ;//構建選擇調節矩陣6. ;//構建局部優化矩陣7. ;//修正相似矩陣8. 對更新后的相似矩陣S使用譜聚類算法;9. //修正結果矩陣10. 更新π視角聚類中心;11. end for 12.end for 13.return Call;

3 核心矩陣的構建

這里我們提出針對兩種實例的處理方法,其中包括選擇調節矩陣的構建和局部優化矩陣的構建,選擇調節矩陣主要是利用多個視角中可識別節點協同訓練的作用,對可識別節點間相似度權值進行強促進或弱促進處理,其目的在于集成各視角中由可識別節點組成的部分社團結構.局部優化矩陣則是對各視角中不可識別節點進行聚類,這里利用機器學習中的核嶺回歸分析方法,將每個不可識別節點的鄰居節點社團劃分結果做為訓練集,以估計不可識別節點最終的社團歸屬并對最終社團結構進行完善.

3.1 選擇調節矩陣

在這里我們要定義可識別節點對視角π進行更新的調節矩陣,利用共識矩陣(co-association)原理,計算各視角中可識別節點的同簇劃分概率,通過概率大小值來調節視角π的原始相似度矩陣,構建方法如公式(1)所示:

公式(1)中,不同于傳統的共識矩陣構建方法,為了解決了其他視角的過度調整問題,使其計算同簇劃分概率中分子的比重不同,如果兩個同社區的實例在其他多個視角中也在同一個社區,則我們將這種促進作用放大;如果兩個非同社區的實例在其他多個視角中屬于同一個社區,雖同樣有促進作用,其分子影響比重較小.所以,上式中可以認為選擇調節矩陣是促進關系結構的過程,不存在其他視角的抑制作用而導致的過度性調整,只有當兩個實例在所有視角中都屬于同一個社團結構時,式中的同簇劃分概率為1,影響值2.7(e1),屬于強促進,其他多種情況均為弱促進.

公式(2)表示π視角與其他視角可識別節點關系聚類情況的整合.例如,節點i和節點j在π視角中同一個社區,并且在其他h(h＜d)個視角中也在同一個社區,那么節點i和節點j在同一個社區的概率會變大,促進作用會大幅度增強.

公式(3)表示其他視角中聚類效果明顯的實例對,對視角π是有促進作用的.如果節點i和節點j在其他大多數視角中屬于同一個社區結構,那么節點i和節點j在同一個社區的概率也會變大,促進作用會小幅度增強.

下面用3個實例的關系來展示該更新過程.假設我們得到3個視角關系的聚類結果矩陣,如圖1所示.其中3個視角的實例集聚類結果分別為{(a,b)(c)(d,e)},{(a,b,d)(c)(m)(e,t)},{(a,b,c)(m)(d,e)}.

圖1 3個視角的聚類結果矩陣

圖2可以看出,由于3個視角的共同影響,實例A與實例B在同一個社區的可能性比較大,在3個視角中都是強促進關系.在第1個視角中,盡管實例c和實例d沒有與實例a,b劃分到一個簇中,但在其他視角的作用下對其相似度關系會起到弱促進的作用,同理e和d;在視角2中,m實例在視角3中也出現了但其聚類結構中沒有和其他節點有任何促進關系,所以我們也可以將其當作不可識別節點處理,參加不可識別節點局部優化矩陣的構建,這里t為不可識別節點;在視角3中實例c在本視角中和a,b實例同簇,在其他視角中無促進作用,所以在該視角中仍然作不可識別節點處理來避免其劃分不準確的問題,如果節點c與節點a和節點b的關聯度大則在下節優化矩陣構建中仍然為同簇.

圖2 3個視角的選擇調節矩陣

3.2 局部優化矩陣

局部優化矩陣的構建是利用局部學習和聯合訓練相結合的方法,應用監督學習的思想來解決無監督學習中的聚類問題.我們將每個視角中無法通過其他視角進行聯合聚類的節點集稱為不可識別節點集,那么局部優化矩陣構建的基本原理,就是基于核嶺回歸函數[15],利用節點的鄰居節點來估計不可識別節點集的劃分.通過提出優化函數的方式來得到不可識別節點集的最好的聚類結果如公式(4)所示:

其中,n表示不可識別節點個數,c表示聚簇個數,表示節點i在l聚簇中的標簽值,這里Fn×c為標準劃分矩陣(FTF=I),公式中表示核向量機的輸出函數[16],利用核函數的監督方法,訓練節點i的鄰居節點標簽集,得到其在聚簇l下的估測劃分值.其中的計算如公式(5)所示:

其中K(xi,xj)是徑向基核函數,這里xi為核函數中心,Ni表示xi的鄰居節點集,β為回歸參數.

3.2.1 利用核嶺回歸計算F

我們將求解公式(4)的問題轉換成求解公式(6)的問題:

其中,Ki為xi鄰居節點集的相似矩陣,表示向量這里利用核嶺回歸(KRR)算法求得公式(6)中回歸參數為帶入公式(5)得公式(7):

3.2.2 獲得最終局部優化矩陣L

根據文獻[17,18]中的聚類算法,使用(PM)P表示聚類劃分結果,其中如果表示xi在l聚簇中且上文中我們先使用標準劃分矩陣(PM)F表示劃分結果,其中F的初始定義為這里通過公式(10)可得到劃分矩陣P.

上式中I是單位矩陣,根據F矩陣可以很容易的得到非標記節點的劃分L矩陣如公式(11):

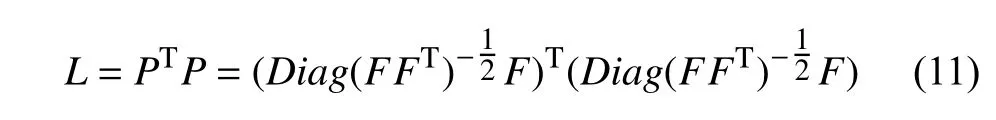
4 實驗

4.1 實驗環境和數據集

本文我們主要使用來自于UCI數據庫的Iris和Wine數據集和DBLP數據集進行測試實驗.Iris數據集包含150個鳶尾花實例樣本,每個實例包含4個屬性(花瓣長度,花瓣寬度,葉子長度,葉子寬度)進行描述,Wine數據集與Iris數據集基本類似,包含178個葡萄酒樣本,每個實例有13個屬性信息(化學分析指標)描述,其中如表1所示,實驗中,隨機選取幾種屬性構成一個多視角結構,節點為實例向量,邊的權值表示各實例間的相似度值,聚類結果將數據集分配到各自類別中.

表1 UCI數據集

DBLP數據集我們提取了與數據庫方向相關的 4個會議(SIGMOD,VLDB,ICDE,SIGKDD)的作者及論文,作者總數為9628,論文總數為10175.每個會議形成一個社會網絡,節點為作者,邊表示作者間協作關系.最終形成的每個社區將代表具有相似研究興趣的課題小組.如表2所示.

表2 DBLP數據集

4.2 評價指標

規范化互信息(Nomalized Mutual Information,NMI)[19]用來度量網絡的真實結構與經過算法所得到的聚簇結構的相似性.假定兩個集合向量X和Y,NMI的定義如公式(9)所示,NMI的取值為0～1之間,取值越大(接近1時),表示聚類結果越精確.

模塊度評價方法[20]是一種基于內部標準的聚類效果衡量指標,一般用于沒有已知的聚簇結果對比時衡量聚類效果的優劣.模塊化是指網絡中連接社區結構內部節點的邊所占的比例和另一個隨機網絡中連接社群結構內部節點的邊所占比例的期望值之差.

模塊度的計算如公式(13)所示,取值范圍在0到1之間,并且值越接近1表示簇內越緊密而簇間越分離.

4.3 性能評估

實驗1.本實驗比較Wine數據集和Iris數據集的多視角聚類結果.Wine數據集中隨機選取4個屬性表示4個視角,同理,Iris數據集中選取3個視角,分別比較節點重合率為100%、75%、50%、25%條件下的協同聚類結果,如圖3至圖10所示,從圖中可以看出,隨著各個視角中相同點個數的增加,社區發現的準確率逐漸提升,當重復率為100%時,迭代過程就變成傳統的多視角聚類算法.同時,對于屬性條件區分能力差的視角,通過其他視角的相互影響,能夠有效提高該視角社區發現的準確性.并且,隨著迭代次數的增加,每個視角中可識別節點的局部社區結構得到集成處理,各個視角的聚類結果都呈現收斂的狀態.

圖3 Wine多視角協同選擇聚類(重合率100%)

圖4 Wine多視角協同選擇聚類(重合率75%)

圖5 Wine多視角協同選擇聚類(重合率50%)

實驗2.圖11和圖12是顯示在同樣覆蓋率的條件下,將3個視角的聚類精度與2個視角聚類精度進行比較,可以看出3個視角的屬性關系比2個視角的屬性關系達到收斂狀態后精度更高,表明視角越多所包含的實例關系屬性越完全,聚類效果越好.這里我們選取100%覆蓋率,是保證1視角和2視角的初始聚類精度相同.

圖6 Wine多視角協同選擇聚類(重合率25%)

圖7 Iris多視角協同選擇聚類(重合率100%)

圖8 Iris多視角協同選擇聚類(重合率75%)

圖9 Iris多視角協同選擇聚類(重合率50%)

實驗3.本實驗將co-MLSC算法和CSC及CS算法算法進行比較,各視角間節點集重合率為75%,從圖13中可以看出,當將譜聚類算法選取固定的最優聚類中心的時候,單視角的聚類結果呈持平狀,說明在單視角聚類中CS算法聚類結果已達到最優狀態.當重合率為75%的時,不能直接使用CSC算法,所以我們必須將各視角中的非識別節點添加到其他視角中并將相似度進行填0處理.CSC的過度調整過程使低精度視角明顯影響高精度視角的走勢.通過比較可以看出co-MLSC算法并沒有過度調整的缺點.

圖10 Iris多視角協同選擇聚類(重合率25%)

圖11 2個視角的Iris數據聚類結果趨勢圖

圖12 3個視角的Iris數據聚類結果趨勢圖

實驗4.使用DBLP數據集構建真實的基于作者協助關系的多維網絡,由于數據的重復率普遍較低,所以我們進行了一定的人工調節,刪除合作者為1的論文,并對作者統一ID值,然而若將數據重復率控制太高的話每個領域內數據數目將非常少,所以我們只能將數據集的重復率控制在 40%以下進行變化,具體實驗結果如圖14所示.這里我們僅取SIGMOD,VLDB,ICDE3個視圖關系結構,該實驗表現了本文提出的局部協同聚類算法在數據重復率較低的情況下有促進其他視角的作用,并且也體現出該算法在真實構建的多維網絡中有很好的適用性.

圖13 co-MLSC、CSC、CS算法的比較結果圖

圖14 DBLP數據集社團發現精度走勢

5 總結

針對現有社區發現技術的不足,本文提出一種基于局部協同選擇聚類的多視角社區發現算法co-MLSC,該算法充分考慮了各視角間聚類的協同作用,利用聯合選擇的方法相互促進來確定聚類中心結構,同時也是對多個視角的聚類中心進行融合的過程,以此來提升社區發現的準確性.另外,使用核嶺回歸估計的方法將每個視角下的不可識別節點進行劃分,最后通過實驗驗證了該算法的可行性和有效性.

下一步工作將對迭代式協同聚類算法的計算復雜度進行分析,提出優化策略來降低社區發現算法的執行代價.

1 Tang L,Wang XF,Liu H.Uncoverning groups via heterogeneous interaction analysis.Proceedings of the 9th IEEE International Conference on Data Mining.Miami Beach,FL,USA.2009.503–512.

2 Kanungo T,Mount DM,Netanyahu NS,et al.An efficient K-means clustering algorithm:Analysis and implementation.IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):881–892.[doi:10.1109/TPAMI.2002.1017616]

3 Ng AY,Jordan MI,Weiss Y.On spectral clustering:Analysis and an algorithm.Advances in Neural Information Processing Systems 14.2001.

4 Shi JB,Malik J.Normalized cuts and image segmentation.IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888–905.[doi:10.1109/34.868688]

5 Kuang D,Dingo C,Park H.Symmetric nonnegative matrix factorization for graph clustering.Proceedings of the 2012 SIAM International Conference on Data Mining.Anaheim,CA,USA.2012.106–117.

6 Xu W,Liu X,Gong YH.Document clustering based on nonnegative matrix factorization.Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.Toronto,Canada.2003.267–273.

7 Strehl A,Ghosh J.Cluster ensembles-a knowledge reuse framework for combining multiple partitions.The Journal of Machine Learning Research,2003,(3):583–617.

8 Christoudias CM,Urtasun R,Darrell T.Multi-view learning in the presence of view disagreement.Proceedings of the 24th Conference on Uncertainty in Artificia lIntelligence .Helsinki,Finland.2008.

9 Muslea I,Minton S,Knoblock CA.Active +semi-supervised learning=robust multi-view learning.Proceedings of the 19th International Conference on Machine Learning.San Francisco,CA,USA.2002.435–442.

10 Chaudhuri K,Kakade SM,Livescu K,et al.Multi-view clustering via canonical correlation analysis.Proceedings of the 26th Annual International Conference on Machine Learning.Montreal,Quebec,Canada.2009.129–136.

11 Kumar A,Daumé H.A co-training approach for multi-view spectral clustering.Proceedings of the 28th International Conference on Machine Learning.Bellevue,WA,USA.2011.393–400.

12 Kumar A,Rai P,Daumé H III.Co-regularized multi-view spectral clustering.Proceedings of the 24th International Conference on Neural Information Processing Systems.Granada,Spain.2011.1413–1421.

13 Niu DL,Dy JG,Jordan MI.Multiple non-redundant spectral clustering views.Proceedings of the 27th International Conference on Machine Learning.Haifa,Israel.2010.

14 Cheng W,Zhang X,Guo ZS,et al.Flexible and robust coregularized multi-domain graph clustering.Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Chicago,IL,USA.2013.320–328.

15 Shawe-Taylor J,Cristianini N.Kernel Methods for Pattern Analysis.Cambridge,UK:Cambridge University Press,2004.

16 Schlkopf B,Smola AJ.Learning with Kernels:Support Vector Machines,Regularization,Optimization,and Beyond.Cambridge,MA:The MIT Press,2001.

17 Chan PK,Schlag MDF,Zien JY.Spectral k-way ratio-cut partitioning and clustering.IEEE Transactions on Computeraided Design of Integrated Circuits and Systems,1994,13(9):1088–1096.[doi:10.1109/43.310898]

18 Yu SX,Shi JB.Multiclass spectral clustering.Proceedings of the 9th IEEE International Conference on Computer Vision.Nice,France.2003.

19 Ng AY,Jordan MI,Weiss Y.On spectral clustering:Analysis and an algorithm.Advances in Neural Information Processing Systems.2002.849–856.

20 Newman MEJ,Girvan M.Finding and evaluating community structure in networks.Physical Review E,2004,69(2):026113.[doi:10.1103/PhysRevE.69.026113]