粗糙元對高超聲速邊界層轉捩影響的研究進展
董 昊, 劉是成, 程克明
(南京航空航天大學 航空宇航學院, 南京 210016)
0 引 言
一直以來,邊界層轉捩就是湍流研究領域的熱點問題,由于其復雜性、現有方法的局限性以及風洞試驗存在較大難度,對邊界層轉捩很多問題的認識或不清楚,或有爭論,甚至還存在許多未知的問題[1]。近年來,隨著高超聲速飛行器的發展,邊界層轉捩問題更加突出。高超聲速飛行器復雜外形產生的復雜流動會導致特殊的邊界層轉捩現象,形成多種轉捩機制并存、湍流區與層流區不斷變化的復雜形式[2]。在實際工程中,邊界層轉捩對高超聲速飛行器氣動設計具有重要影響。具體來說,邊界層轉捩將影響飛行器氣動加熱、表面摩擦阻力、進氣道流量、發動機燃燒效率和工作效率等一系列問題。對于高超聲速飛行器,粗糙元誘導轉捩是重要的轉捩形式之一。通過研究粗糙元不同參數對高超聲速邊界層轉捩的影響,探求粗糙元誘發轉捩的物理機理以及針對工程應用的相關預測準則,具有重要的研究意義。
粗糙元對邊界層轉捩影響的研究從20世紀50年代就已開始,并取得了一系列研究成果,尤其是Schneider等[3-4]開展了大量研究工作,并在其綜述文章中[3]強調了研究的3個主要方向:粗糙元促成轉捩的機理、粗糙元引起轉捩的最小尺寸、粗糙元不能引起轉捩以及不影響轉捩位置的最大尺寸;總結了粗糙元影響轉捩的3種模式:(1)粗糙元會在尾跡區產生流向渦結構和不穩定剪切層。當粗糙元尺寸大于其“有效高度”時,粗糙元下游將立即發生轉捩,但當其尺寸較小時,轉捩可能會在距離粗糙元較遠的下游位置發生,其原因可能是剪切層失穩或尾跡渦失穩誘導所致。(2)當粗糙元尺寸較小時(基于粗糙元高度的雷諾數Rek<10),橫流、G?rtler渦以及瞬態增長機制是導致粗糙元后流向渦增長并最終失穩的原因。(3)來流擾動也是影響粗糙元后流動失穩的原因,如聲波與粗糙元相互作用會產生第一、第二模態的擾動波等。上述結論均是在風洞試驗和飛行試驗數據分析中得到的驗證性結果,缺乏理論的強力支撐。
除Schneider外,Reda[5]、Iyer[6]、羅紀生[7]、陳堅強[8]等在其綜述文章中均對與粗糙元相關的高超聲速邊界層轉捩進行了部分概述。前述文獻主要是針對粗糙元類型(孤立、離散/分布)和自身參數(高度、形狀、間距等)、轉捩控制效果(促進、推遲)等進行綜述。本文側重已有綜述文獻未涉及或未詳細介紹的內容,回顧近年來不同類型粗糙元對高超聲速邊界層轉捩影響及控制的最新研究進展,闡述粗糙元在高超聲速轉捩機理相關研究中的作用,簡要介紹在南京航空航天大學高超聲速風洞(NHW)中開展的部分研究工作,總結展望粗糙元對高超聲速邊界層轉捩影響研究的發展趨勢。
1 粗糙元對轉捩影響的最新研究進展
粗糙元對層流及轉捩的控制,不僅是空氣動力學研究的前沿熱點問題之一,其在高超聲速飛行器氣動力和氣動熱設計中也占有重要地位,具有重大的工程應用價值。一方面,高超聲速飛行器表面防熱瓦之間有一些填充物,當這些填充物受熱發生變形,形成飛行器表面的凸起和凹陷,這種大的粗糙元或者小的粗糙度可以誘發邊界層轉捩。根據美國國家航天飛機(NASP)項目的經驗,由于湍流的熱傳導率比層流大很多,飛行器在全層流狀態下的有效載荷與總重量的比值是全湍流狀態下的兩倍左右[9],因此,必須采取一定措施來抑制層流向湍流的轉變。另一方面,在高超聲速吸氣式飛行器設計中,保證進氣道入口處的湍流狀態可以為推進系統提供足夠的進氣流量,并可促進燃燒室中空氣和燃料的混合。因此,通常在飛行器前體或進氣道入口前一定距離處放置粗糙元或粗糙帶,人工促使流動從層流轉變為湍流。在美國X-33、X-43和X-51等高超飛行器驗證計劃中,都對該類轉捩形式給予了極高重視[10-13]。
1.1 高超粗糙元的分類
開展粗糙元對高超聲速轉捩控制研究的首要工作是對高超粗糙元進行合理分類。通常情況下,從幾何形狀上,高超粗糙元可以分為規則(regular)和不規則(irregular)兩類;從分布形式上,高超粗糙元亦可分為孤立(isolated)和離散/分布(discrete/distri-buted)兩類。本文將以上兩種分類方式結合,對高超粗糙元進行分類,如圖1所示。

圖1 高超粗糙元分類
按分布形式,規則粗糙元可分為孤立、離散兩類。孤立粗糙元又可分為二維和三維粗糙元。當粗糙元某個方向的尺度遠大于另外兩個方向,可視為二維粗糙元。常見的二維粗糙元有展向臺階、凹腔等。三維粗糙元則通常表示粗糙元尺度在三個方向上大小相似,比如圓柱、方形、菱形等規則的凸起或者凹腔。當許多孤立的規則粗糙元以某一特定規律集中分布于一塊區域,可以稱之為離散式粗糙元,如不同形狀、間距、高度/深度的粗糙元凸起/多孔壁面,此時的流動通常會受到各粗糙元分布參數的影響。同樣,不規則粗糙元也可分為孤立和分布的不規則粗糙元(度)。在實際飛行中,高超聲速飛行器往往會遭遇物理損傷或高溫燒蝕,在其熱防護系統(Thermal Protection System,TPS)上形成形狀不規則的凸起或凹陷。一般情況下,物理損傷多為單一形式,即孤立不規則粗糙元;表面由于氣動加熱燒蝕或融化形成的凹凸不平,如砂礫結構、蜂窩結構等,則屬于典型的分布式粗糙度。
下文將開展規則和不規則粗糙元對高超聲速轉捩影響相關研究的綜述:主要敘述規則高超粗糙元研究中較為集中的表面凸起粗糙元,簡要介紹凹腔和多孔壁面對高超聲速轉捩影響的研究進展;不規則高超粗糙元方面,則主要總結說明分布式粗糙度對高超聲速轉捩影響的研究進展。
1.2 規則粗糙元對高超聲速邊界層轉捩影響研究
1.2.1表面凸起粗糙元
形狀規則的表面凸起粗糙元是最為常見的高超聲速邊界層強制轉捩裝置[14],研究者已開展了大量研究工作[15-19]。影響此類粗糙元對轉捩控制效果的因素很多,如粗糙元的幾何參數(高度、寬度、形狀、相鄰粗糙元的間距)、當地邊界層厚度、來流雷諾數與馬赫數[20]、迎角、壁溫、自由流湍流度[21]等。對于孤立表面凸起粗糙元,大多數對其控制轉捩機理及效果的研究主要集中于幾何參數;而在眾多幾何因素中,粗糙元的高度[22-23]對轉捩效果起著最為重要的作用。
圖2顯示了典型的球狀粗糙元的高度對可壓縮邊界層轉捩的影響[22],對應的馬赫數范圍為1.97~3.84。從圖中可以看出,當粗糙元高度高于“有效高度”時,粗糙元會對邊界層轉捩位置造成一定影響;而當粗糙元高度達到所謂“臨界高度”時,轉捩會在粗糙元處立即發生。
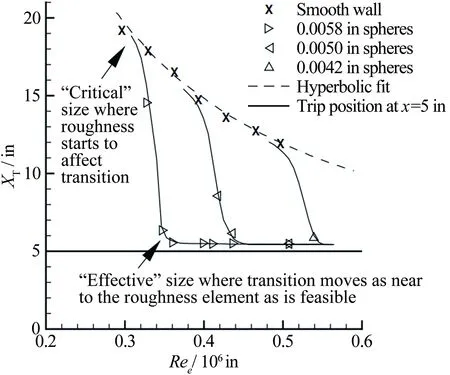
圖2 粗糙元臨界高度和有效高度[22]
Wheaton等[23]在普渡大學Boeing/AFOSR Mach 6靜風洞中系統研究了圓柱形粗糙元不同高度(0.2~1.2倍當地邊界層高度)對轉捩的影響及相應的物理機理。研究發現,粗糙元高度較低時,其后方尾流中的擾動主導頻率為40~70kHz;當粗糙元高度增加至對應的雷諾數Rek大于6×104時,擾動主導頻率變為20~25kHz。這說明粗糙元高度的變化必然會引起感受性、失穩機理的改變,但其根本原因和影響規律還不得而知。
另外,孤立表面凸起粗糙元的形狀也是影響轉捩控制效果的主要因素。斜坡、鉆石、正方形、半球形和圓柱體是典型的粗糙元形狀,不同形狀的粗糙元誘導轉捩機理和效果并不相同。Zhou等[24]系統研究了不同馬赫數下(Ma=3.37~6.63)不同粗糙元形狀對轉捩的控制效果,發現方形、鉆石形粗糙元誘導轉捩效果明顯優于圓柱形和半球形;并且,隨著馬赫數的提高,粗糙元誘導的轉捩位置延后,表明壓縮性對粗糙元的誘導轉捩效果有很大影響。朱德華等[25]利用DNS研究了Ma=6來流條件下斜坡形、對齒形粗糙元誘導轉捩的特性以及工程應用。研究表明,相較于斜坡形粗糙元,對齒形粗糙元具有多種渦結構失穩模式,因而具有更強的誘導轉捩能力和更低的有效高度,其能夠有效誘導轉捩對應的飛行范圍更為廣泛。
與孤立粗糙元相比,離散式表面凸起粗糙元對高超聲速邊界層轉捩的影響更為復雜[3]。離散式粗糙元引起的擾動源遠多于孤立粗糙元,因此很難區分不同擾動源在誘導轉捩過程中的主導作用。盡管在離散式粗糙元對高超聲速邊界層轉捩控制效果的研究中發現,相鄰粗糙元的間距往往是關鍵影響參數,但其原因至今尚無明確解釋。Whitehead等[26]系統探討了圓柱形離散式粗糙元間距對高超聲速邊界層轉捩的影響,發現當s/w>3(s為粗糙元間距,w為粗糙元寬度)時,粗糙元間距對轉捩過程沒有影響;當s/w<3,孤立粗糙元周圍的流場會受到相鄰粗糙元的強烈影響而加快轉捩的發生;但當相鄰粗糙元十分接近時,轉捩的促進效果反而又降低了。最近,Duan和Xiao[27]利用DNS研究了來流馬赫數6時、相鄰斜坡形粗糙元間距對高超聲速邊界層轉捩的影響。結果表明,隨著相鄰粗糙元間距的減小,尾跡渦之間存在相互干擾,從而導致轉捩提前發生。
近年來,隨著大規模計算條件和先進實驗測量技術的應用和發展,研究者發現了更多的粗糙元對高超聲速邊界層轉捩控制的細節。在數值模擬方面,Duan[28]等利用DNS研究了孤立圓柱形粗糙元誘導的高超聲速邊界層轉捩。數值模擬結果表明,馬蹄渦和粗糙元后剪切層的不穩定性是影響邊界層轉捩的主要因素。Subbareddy[29]等采用動力學模態分解(DMD)方法,對粗糙元產生的馬蹄渦和分離剪切層的演化進行了較為深入的研究。研究結果顯示,頻率為20、40和53kHz的3種擾動模態,分別代表非定常馬蹄渦及其諧波模態以及上卷的剪切層模態,如圖3所示。
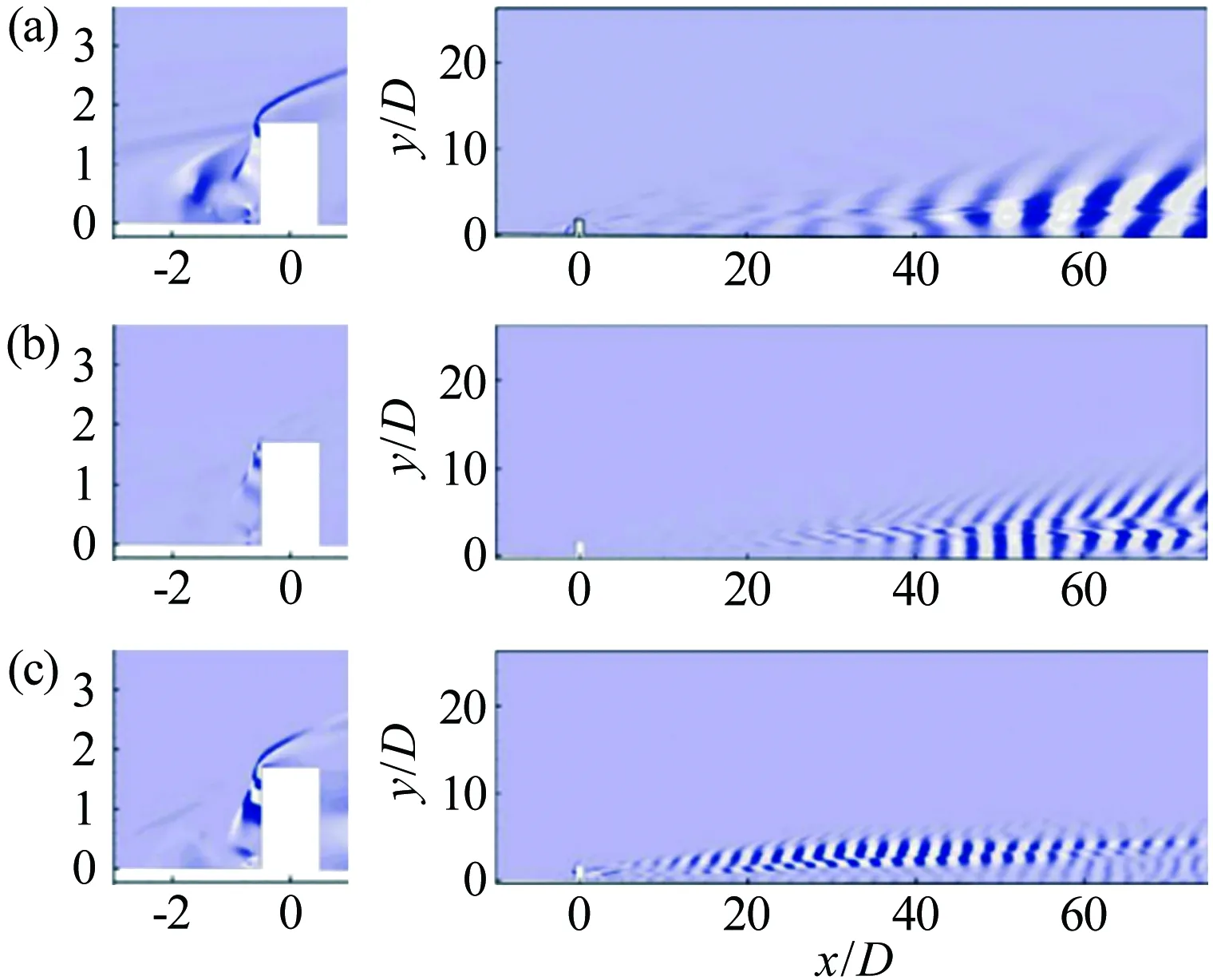
圖3 基于DMD的粗糙元尾跡模態顯示((a), (b), (c)分別表示20、40和53kHz的3種擾動模態)[29]
Fig.3VisualizationofdifferentmodesinthewakeofroughnesselementsbasedontheDMDmethod(a,b,crespectivelydenotethreedisturbancemodesof20,40and53kHz)[29]
在風洞實驗方面,Danehy等[30]利用一氧化氮平面激光誘導熒光(NO-PLIF)方法研究了來流馬赫數為10、帶有半徑2mm半球的平板上的高超聲速邊界層流動,由NO-PLIF圖像確定的邊界層厚度與數值模擬結果一致。在普渡大學Mach 6靜風洞中,Wheaton等[31]首次對粗糙元引起的高超聲速層流邊界層的不穩定性進行了全面的實驗研究。Wheaton利用皮托探針、熱線探針和壁面高頻壓力傳感器對粗糙元尾跡中的脈動信號進行了檢測。結果表明,沿著粗糙元尾跡,不穩定性的振幅逐漸增大,無量綱化的質量流量脈動值接近35%。另外,隨著粗糙元高度的減小,這種不穩定性逐漸減弱并最終消失。Ye等[32]利用三維層析粒子圖像測速技術(Tomo-PIV),研究了Ma=6.5流場下、微型斜坡粗糙元下游的高超聲速邊界層的轉捩特征,發現最大速度波動集中于靠近斜坡粗糙元中心處的低速區域,即流向渦附近。在北京大學Mach 6靜風洞中,Tang等[33]利用多種測量手段研究了帶二維粗糙元的平板邊界層的穩定性,并且利用近壁粒子圖像測速技術(Near-wall PIV)首次拍攝到了第二模態不穩定波經過粗糙元的瞬時速度場和流動結構。結果表明,二維粗糙元能夠成功抑制第二模態不穩定波的發展,如圖4所示。在中國空氣動力研究與發展中心的Ф500mm高超聲速風洞中,Zhao等[34]利用基于納米粒子的平面激光散射技術(NPLS),在來流馬赫數5時對9個分布式斜坡形粗糙元誘導的平板邊界層轉捩進行了實驗研究,并與隱式大渦模擬(ILES)的結果進行了對比。研究發現,風洞中粗糙元誘導的轉捩位置比相同狀態下數值模擬的靠前許多,該項研究將原因歸結于風洞來流噪聲或數值模擬中的耗散。
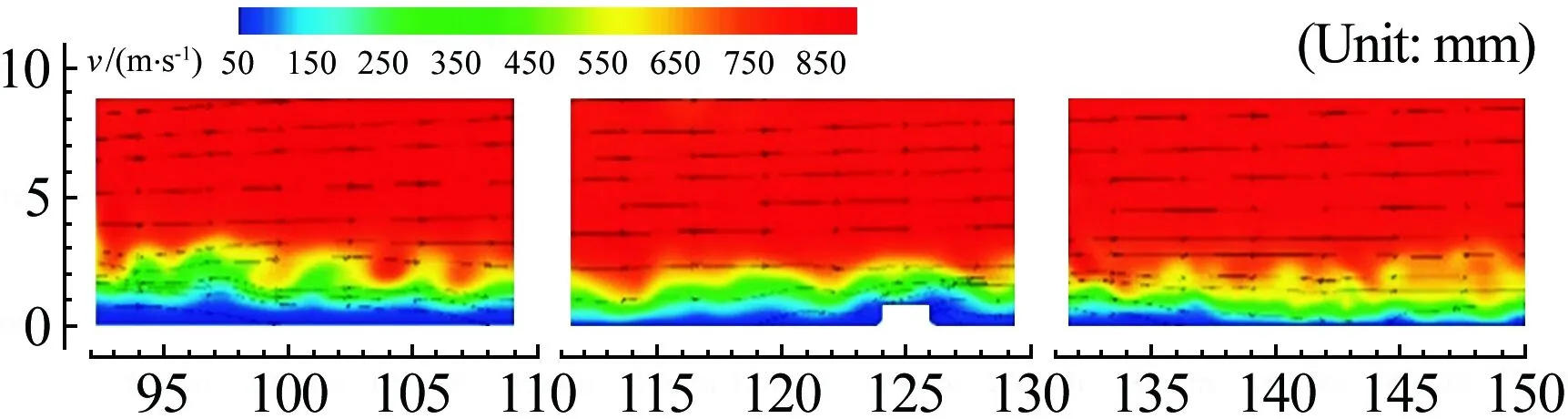
圖4 粗糙元上下游瞬時PIV流場圖[33]
Fig.4InstantaneousPIVflowfieldofupstreamanddownstreamofroughnesselement[33]
1.2.2表面凹腔
早期研究表明,在高超聲速邊界層流動中,表面上的縫隙或凹腔會引起下游區域過早地從層流轉捩到湍流,導致表面摩擦阻力和熱流密度快速增加,進而影響高超聲速飛行器的氣動力和氣動熱性能[35]。針對凹腔流動,前人已經進行了大量數值模擬和風洞實驗研究。
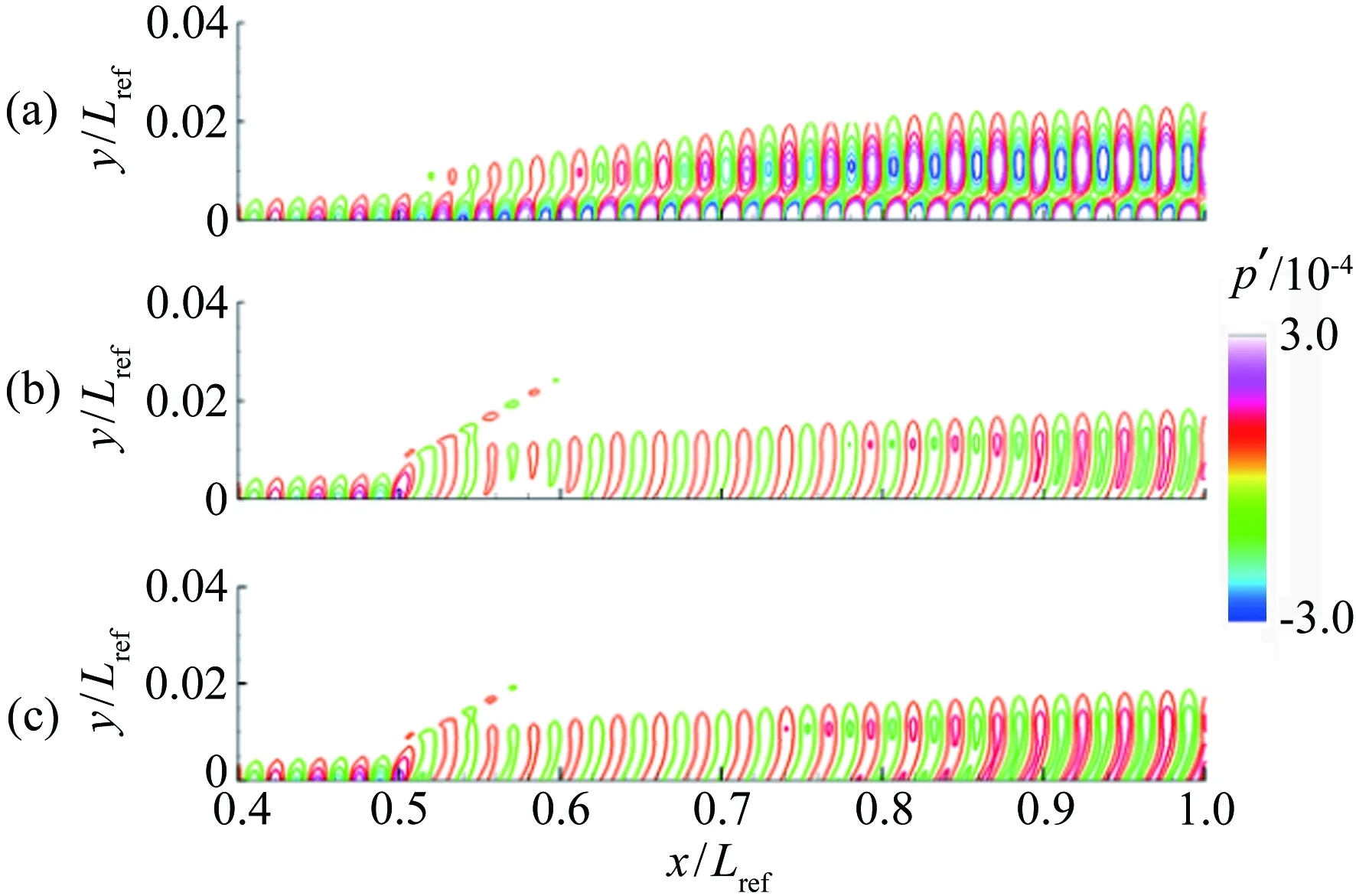
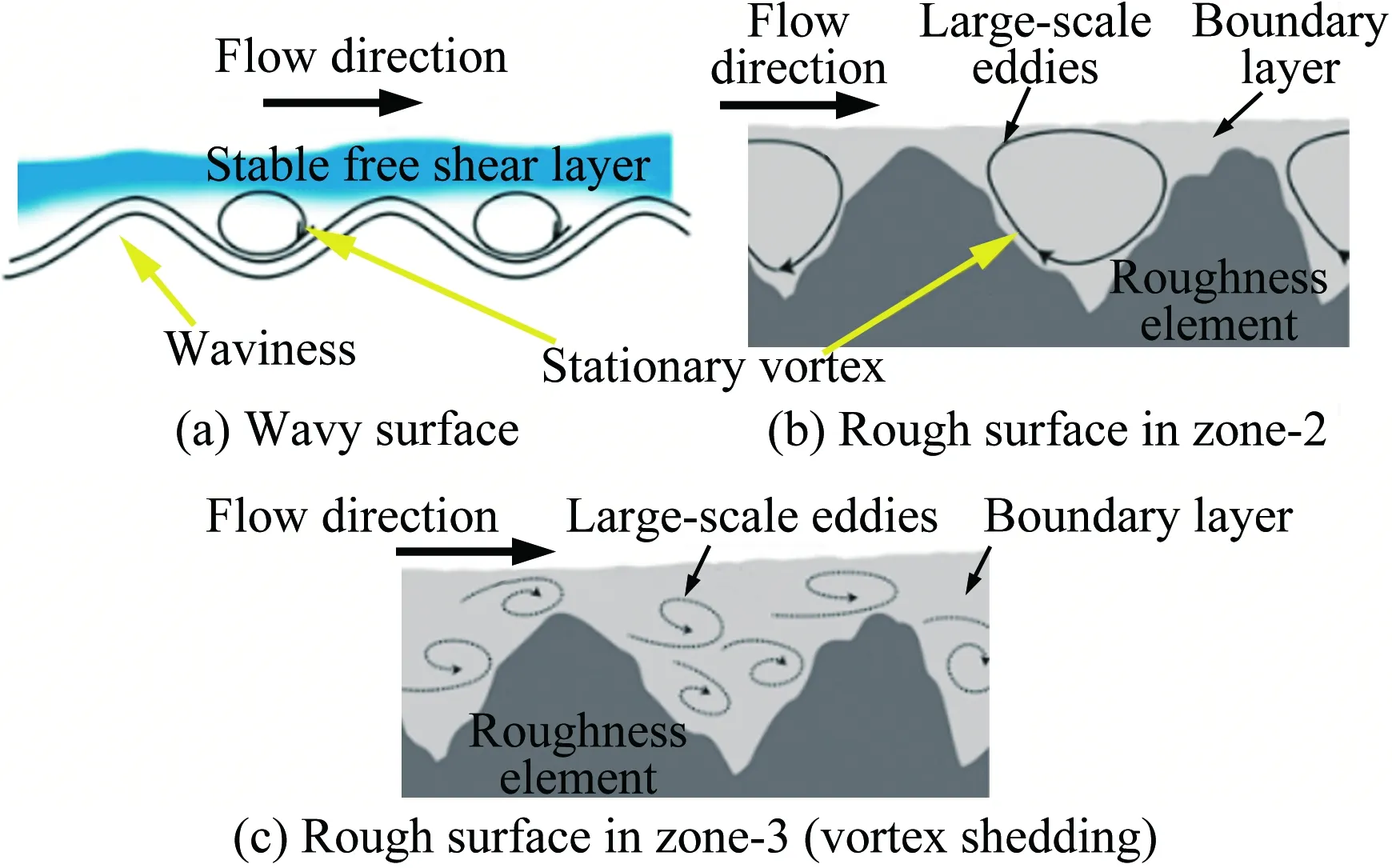
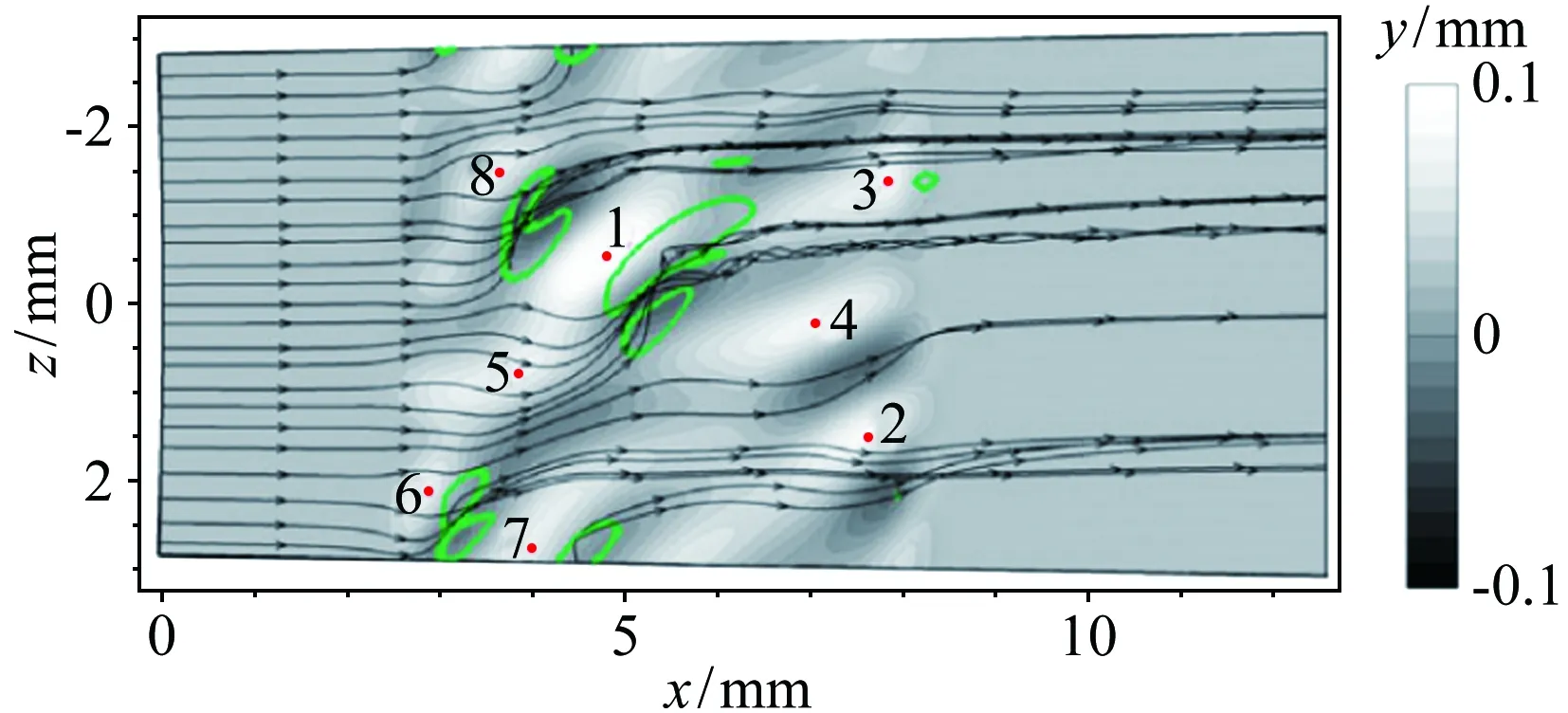
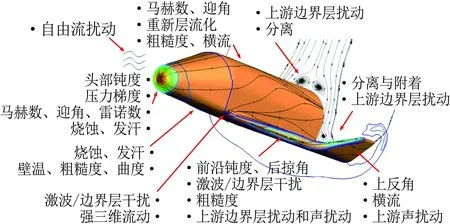
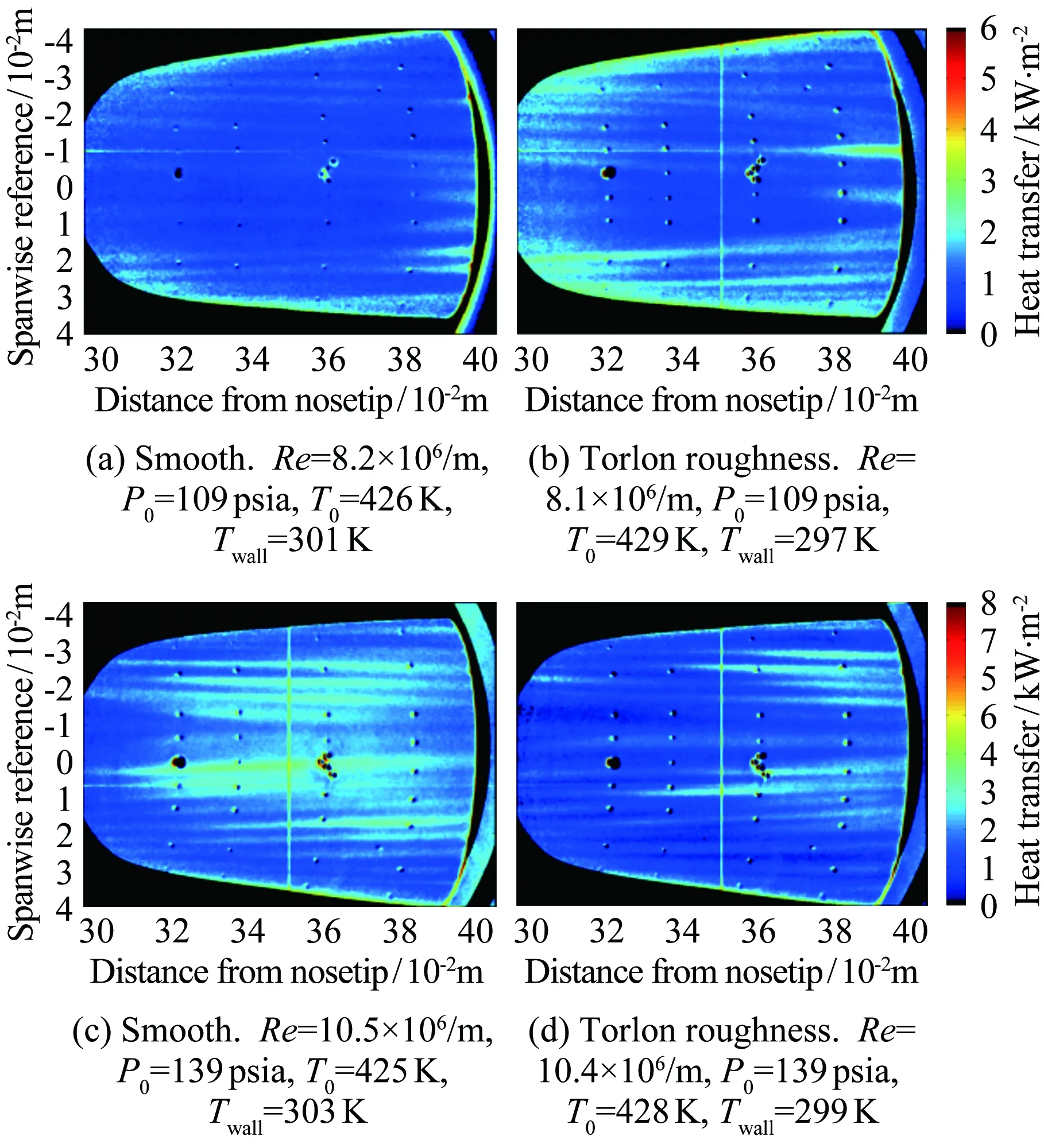
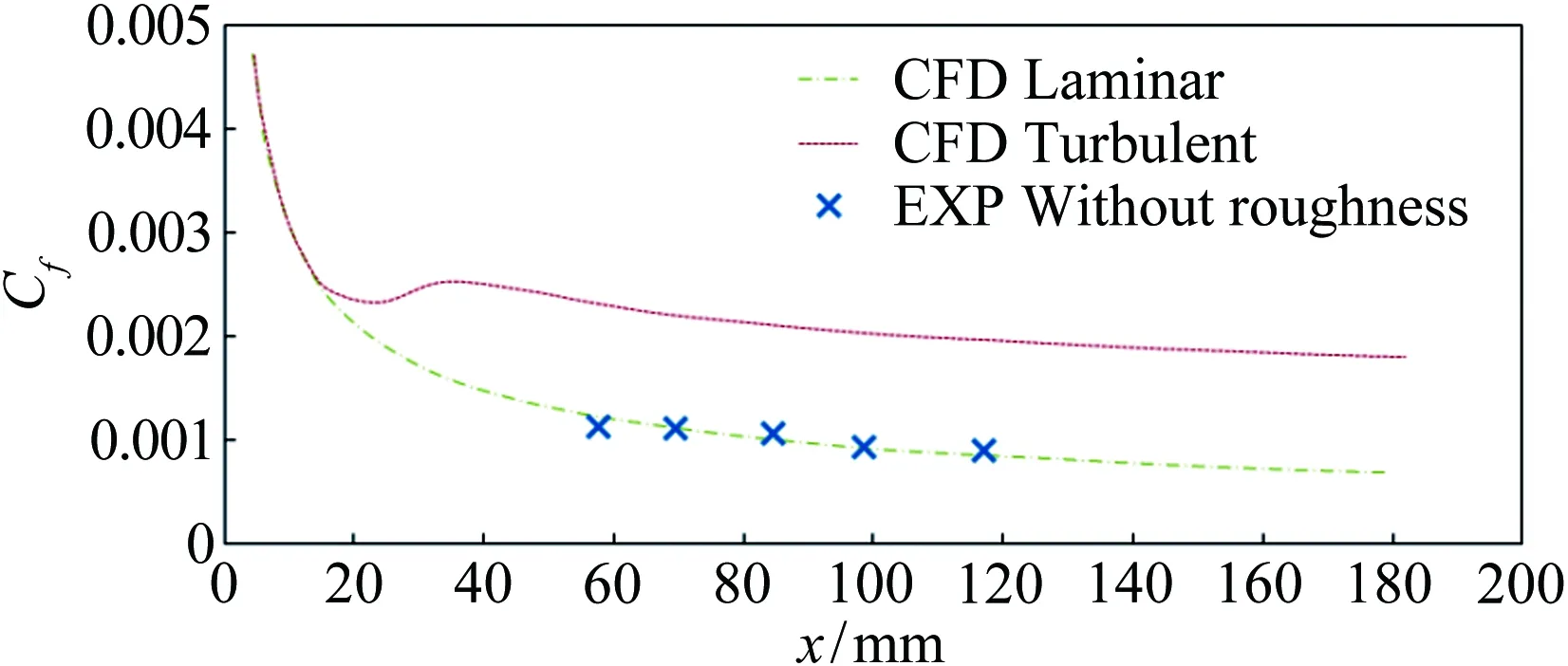
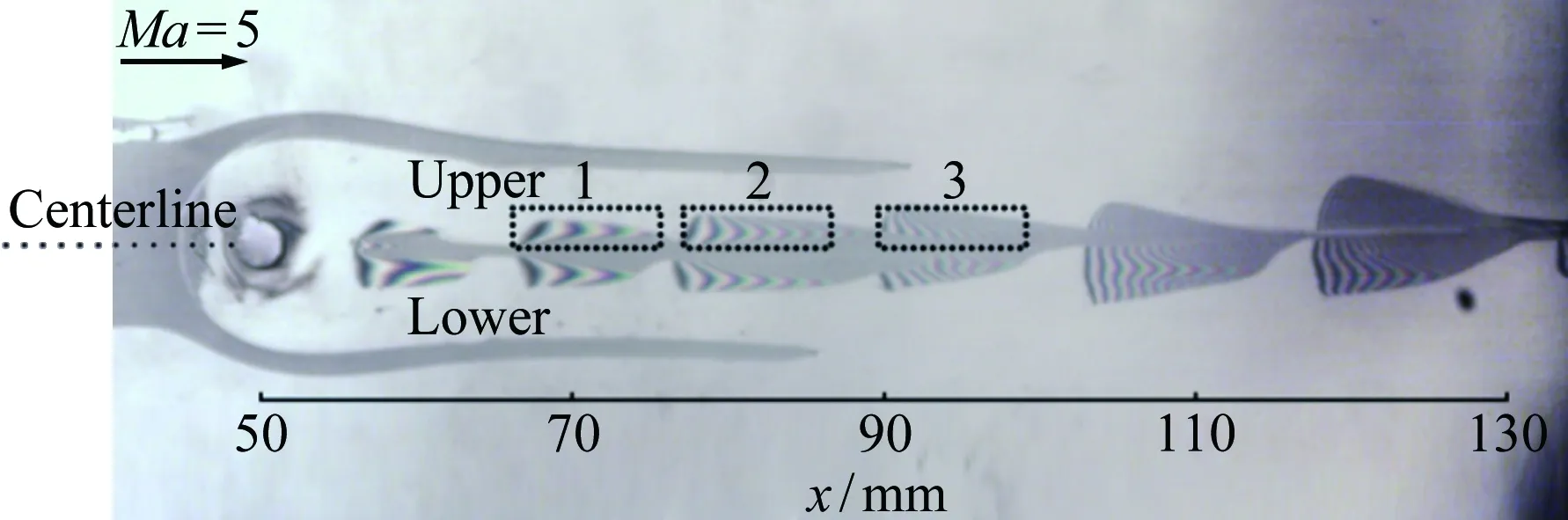
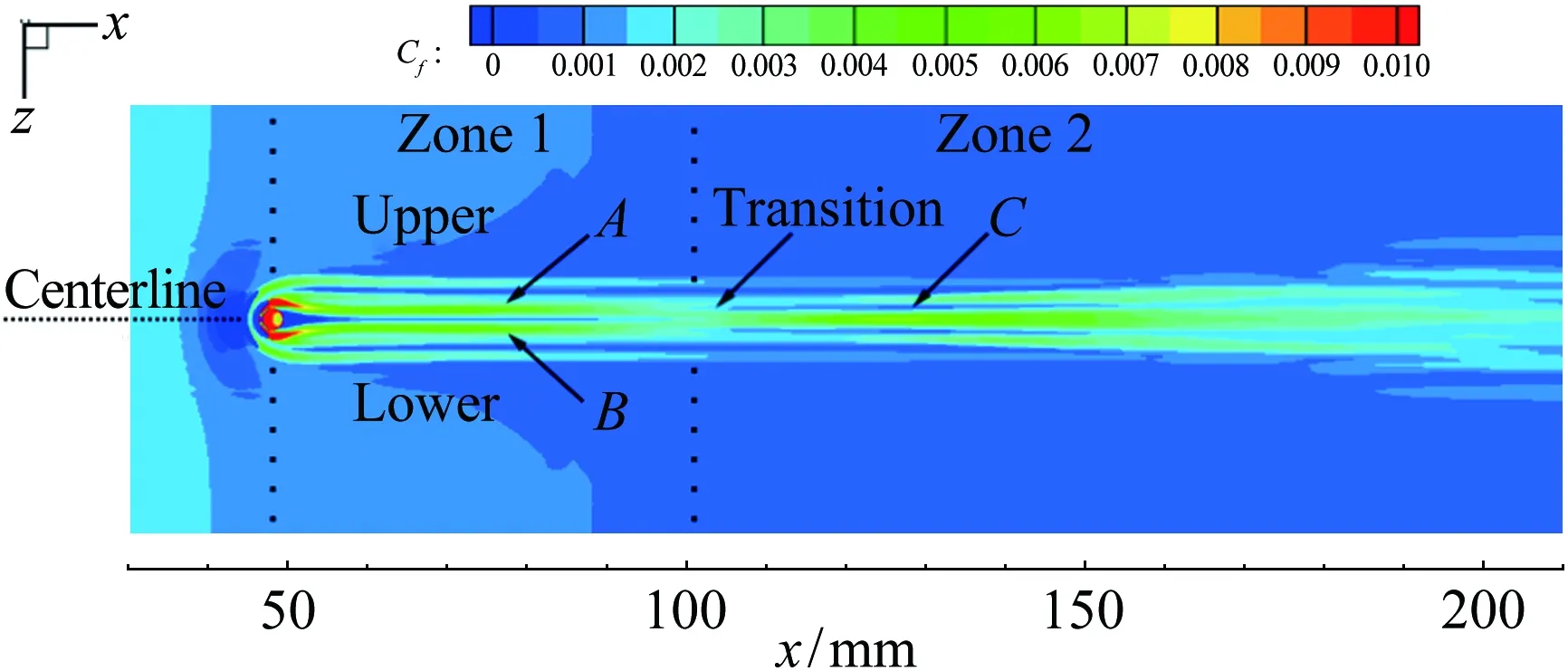
Lawson和Barakos[36]詳細綜述了高超聲速下凹腔對轉捩的影響,認為凹腔可導致發夾渦的自發脫落和尾流的不穩定,且凹腔誘導轉捩的促進作用與凹腔幾何結構密切相關。對于二維凹腔,往往以長深比(L/D)的大小來定義“開腔”“過渡腔”和“閉腔”三種流動狀態。當L/D<10,此時的流動稱為“開腔”流動,在“開腔”流動中,回流會填滿整個腔體;當L/D>14,則稱為“閉腔”流動,此時凹腔內的回流區不能延伸到整個凹腔,就像是后臺階流動和前臺階流動的組合;當10 近年來,高超聲速凹腔流動對邊界層轉捩影響的研究逐漸增多。Ohmichi和Suzuki[38]利用數值模擬和風洞實驗研究了Ma=7條件下帶三維矩形凹腔的平板流動。研究發現,凹腔在其內部和外部誘導了流向的渦結構,這些渦增強了凹腔內壁及下游區域的加熱速率,促進了層流到湍流的轉捩過程。Chang等[39]利用DNS研究了圓柱形凹腔對高超聲速(Ma=6)邊界層轉捩的影響。研究發現,當雷諾數逐漸升高,圓柱形凹腔尾流中存在發夾渦結構脫落現象,且造成了下游壁面溫度升高、剪切層失穩,如圖5所示。 圖5 圓柱凹腔引起的發卡渦結構[39] 為研究三維凹腔誘導轉捩機理,Xiao等[40]采用改進延遲脫體渦模擬(IDDES)方法對三維矩形腔體高超聲速流動(Ma=9.6)進行了研究。研究發現,凹腔在-10°迎角時處于“開腔”狀態,在-15°迎角時為“閉腔”狀態。對于“開腔”狀態,剪切層基本穩定,流動保持層流;對于“閉腔”狀態,外流進入凹腔并撞擊其底部,反射激波和出口激波的存在最終導致流向渦破裂,觸發流動很快轉捩,如圖6所示。 圖6 長方形凹腔引起的流向渦結構(左:-10°,右:-15°)[40] 1.2.3多孔壁面 高超聲速邊界層轉捩控制手段很多,其中很有前景的一項技術是由Fedorov等[41]提出的壁面多孔涂層技術。多孔涂層對主流影響很小,并且能夠有效抑制高超聲速邊界層內最不穩定的第二模態的發展,延遲轉捩的發生[42-44],以上結論已被一些實驗所證實[45-47]。 Wartemann等[48]用數值模擬方法研究了多孔涂層壁面的孔形狀和孔徑對穩定性的影響,結果表明,隨著孔徑增加,產生了額外的阻尼效應。近期,Lukashevich等[49]研究了第二模態對多孔涂層放置位置的敏感性。研究表明,如果涂層在第二模態擾動的不穩定區域內,則對第二模態起到穩定作用,如果涂層在穩定區域內,則會使第二模態不穩定,從而定性地證實了Wang和Zhong[50]之前的數值計算結果。Zhao等[51]建立了一個理論模型來描述平面超聲波在多孔涂層上的聲學特性,該模型考慮了高階衍射模式以及相鄰腔體之間的相互耦合,成功預測了一個與數值結果相符的反射頻率,并使通過該模型優化的腔體幾何參數具有最小的反射系數。結果表明,在Ma=6的平板流場中采用優化后的多孔涂層,Mack第二模態被強烈抑制,最大脈動壓力降低約88%,如圖7所示。 圖7 模型表面瞬時壓力脈動場分布((a) 沒有涂層,(b) 優化后的涂層,(c) 傳統涂層)[51] Fig.7Instantaneousfluctuatingpressurefieldsfor(a)baselinecasewithoutporouscoating, (b)optimizedone,and(c)conventionalone[51] 由此可見,針對規則粗糙元對高超聲速邊界層轉捩的影響,已經形成了較為豐富的理論模型。一方面,不同的規則粗糙元參數(形狀、高度、間距等)對促進轉捩具有不同的影響規律;另一方面,通過設置合適的規則粗糙元參數(高度、間距等),在下游激發特定的渦結構,在一定程度上能夠有效抑制高超聲速邊界層內不穩定擾動的發展,可以起到延遲轉捩的效果。 近年來,Reda開展了許多不規則分布式粗糙度對高超聲速邊界層轉捩影響的相關研究。在NASA的Ames高超聲速彈道靶中,研究了不同幾何構型模型(半球模型[52, 56]、圓錐模型[53-54]、球錐模型[54-56]等)表面分布式粗糙度對轉捩的影響,獲得了大量紋影圖像和表面溫度分布數據。研究發現,對于粗糙度高度小于層流邊界層高度的情況,臨界粗糙雷諾數相關法(Critical-roughness Reynolds Number)能夠很好地反映粗糙錐體表面邊界層的轉捩過程,并且錐頭鈍度對粗糙度誘發的轉捩開始階段和發展階段有重要影響。對于小鈍度錐體,基于粗糙元高度的雷諾數Rek隨粗糙度距頂點距離的增加而增大,且在一定情況下,隨著自由流壓力的增加,轉捩起始位置前移,而Rek基本保持不變,如圖8所示;與之相反,對于大鈍度錐體,Rek隨粗糙度距頂點距離的增加而減小,隨著自由流壓力的增加,轉捩起始位置前移,且Rek逐漸增大[54],如圖9所示。除此之外,Wilder等[56]還模擬了飛行器登陸火星的氣流條件,分析了二氧化碳(CO2)對分布式粗糙度主導轉捩的影響。實驗發現,在CO2氣流條件下,Rek要比空氣條件下偏小。 圖8 小鈍度錐模型及其紋影圖(Ma=10)[54] Fig.8Small-bluntnessmodel, (a)mountedinlaunchsabotand(b)modelinflightatMa=10[54] 圖9 大鈍度錐模型及其紋影圖(Ma=10)[54] Fig.9Large-bluntnessmodel, (a)mountedinlaunchsabotand(b)modelinflightatMa=10[54] 在激波風洞中,Irimpan等[57]研究了馬赫數8.8、單位雷諾數1.98×106/m的來流條件下表面粗糙度對球體壁面熱流的影響。研究發現,球體前部的粗糙度會降低模型表面傳熱性能,其原因可能是由于粗糙空腔中渦旋的持續存在推遲了轉捩。Irimpan進一步分析實驗模型的熱通量數據,發現大范圍的粗糙度使得球體的前體產生了多重空腔效應,如圖10所示。粗糙度形成的空腔可通過捕獲大尺度漩渦來抑制邊界層的不穩定性,將其隔離、限制在這些空腔中,直到更下游區域,漩渦才開始脫落。因此,粗糙表面空腔上方的分離剪切層比光滑表面情況的剪切層更加穩定。 圖10 粗糙表面多腔效應和渦旋動力學效應[57] Fig.10Illustrationofthemultiple-cavityeffectandvortexdynamicsoveraroughsurface[57] Giovanni和Stemmer[58]采用直接數值模擬(DNS)方法研究了鈍頭體上展向周期分布式粗糙度和隨機分布式粗糙度引起的不穩定性機理。基于Ma=5.9來流條件下的半球狀鈍頭體,分析了不同粗糙度后非定常擾動的發展。對于展向周期分布式粗糙度,其尾跡中存在兩個主要的不穩定模態,分別對應于已知孤立粗糙元的對稱和反對稱模態;對于隨機分布式粗糙度,在鈍頭體上觀察到流動在經過不規則粗糙壁面時,流線會出現沿橫向的彎曲,并在背風區域形成大小不一的分離區,這是一種新的由粗糙度誘導的橫流不穩定性,如圖11所示。 圖11 隨機粗糙壁面流線分布(綠色標記為分離區)[58] Fig.11Streamlinedistributiononrandomroughwall(greenmarksseparationzone)[58] 在國內的研究中,張存波[59]利用數值模擬方法研究了分布式粗糙度的高度、波長、區域大小等參數對Ma=4.5的平板邊界層擾動演化的影響。研究結果表明,經過粗糙度時,處在中性曲線以下的低頻擾動會受到抑制,而處在中性曲線以上的高頻擾動幅值會有所增長。 綜上,由于粗糙元構型的復雜性和隨機性,在不規則粗糙元對高超聲速邊界層轉捩影響的研究中難以提煉出統一的理論模型。但由于不規則粗糙元模型更接近高超聲速飛行器表面燒蝕、損傷的真實情況,對其誘導轉捩的機理,還需開展更進一步的研究。 總的來說,在高超聲速邊界層中,無論粗糙元的形式如何(規則或不規則、孤立或分布、凸起或凹陷),粗糙元后方的渦結構對其尾跡區流動的穩定性和轉捩特性都起到了至關重要的作用。 高超聲速流場的本質是高度非均勻、非定常的復雜三維流動,其中存在流動參數變化梯度很大的激波、滑流面、分離剪切層等。與低速和一般可壓縮流動相比,高超聲速邊界層轉捩的影響因素更多,不同影響因素之間還會發生相互作用從而產生新的影響,如圖12所示[8]。因此,對高超聲速邊界層轉捩機理的研究,往往需要把單個影響因素獨立出來進行,盡量避免多因素相互干擾。粗糙元作為主要因素之一,其對邊界層轉捩機理的影響一直以來都是研究的熱點。首先,感受性作為高超聲速邊界層轉捩預測與控制的關鍵環節[60],在國際上越來越受到研究人員的重視;其次,近年來眾多學者對高超聲速三維邊界層轉捩機理的研究表明:對于高超聲速飛行器表面邊界層轉捩現象,橫流失穩是主導因素[61-62]。本文將從粗糙元對高超聲速邊界層感受性問題以及橫流失穩影響的角度,簡述其在高超聲速邊界層轉捩機理中的研究進展。 圖12 高超聲速轉捩影響因素示意圖[8] 為了系統研究和認識邊界層轉捩問題,人們把轉捩過程分為4個階段[63-64]。在其中第一個階段,外界擾動進入邊界層,并在其內部產生不穩定擾動,這就涉及邊界層感受性問題[65-66]。外界擾動不同,邊界層轉捩的位置和機理也會不同。因此,如何確定外界擾動和轉捩的定量關系,是感受性研究的關鍵問題。另外,影響感受性的因素很多,比如來流湍流度、聲擾動、熵擾動、表面幾何形狀和壁面粗糙度等。根據擾動源的不同,可將感受性分為自由流擾動的感受性(聲波、渦波和熵波)和壁面擾動源感受性(粗糙元、壁面震動、周期性抽吸和壁面加熱等)[67],如圖13所示[68]。 圖13 高超聲速邊界層自由流、壁面粗糙度擾動感受性[68] Fig.13Thereceptivityinahypersonicflowinducedbyfree-streamandsurfaceroughnessdisturbance[68] 目前,關于低速邊界層對粗糙元的感受性研究較多,包括離散式粗糙元、分布式粗糙度等[7,69];而粗糙元對高超聲速邊界層轉捩的影響雖是研究熱點,但其影響機制仍未清晰[70-74]。通常情況下,高超聲速邊界層對粗糙元的感受性要比低速邊界層復雜得多,其包含了粗糙元和來流聲波、渦波的相互作用,涉及橫流轉捩、尾跡和瞬態增長等過程。在高超聲速邊界層感受性研究的理論方法中,均采用了一些特定假設條件,如漸進方法[75]、拋物化方程法(PSE)[76]、多模態法[77]等,其帶來的影響并未經過相關實驗檢驗,研究者大多是定性觀察風洞來流擾動與邊界層轉捩雷諾數之間的相關性,風洞實驗無法顯示不同擾動模態如何通過激波以特定的色散關系進入到邊界層內,并進一步觸發邊界層內擾動增長的過程[78]。另外,感受性處于高超聲速邊界層轉捩的初始階段,其擾動幅值非常低。一方面,為避免風洞噴管壁面湍流邊界層產生的擾動對感受性研究的干擾,要求在研究中盡可能采用靜風洞,而靜風洞因其設計復雜、造價昂貴并未普及;另一方面,小幅值擾動及其發展超出了常規高超聲速風洞實驗技術的測量范圍。因此,對高超聲速感受性的實驗研究十分有限。2001年前后,Maslov等在Ma=6來流中,測量了平板邊界層對二維、三維聲波的感受性系數,發現感受性系數與三維擾動波的迎角、幅值均無關,在0°迎角下,三維擾動的感受性系數約為二維擾動的1/5~1/6[79]。最近,Lee在北京大學Ф300mm高超聲速靜音風洞中,利用CO2瑞利散射流動顯示和近壁粒子圖像測速技術(Near-wall PIV),研究了AC放電引入的人工擾動對來流馬赫數6.5時的平板邊界層轉捩的影響,同時指出粗糙元通常對高超聲速感受性有3種影響:粗糙元高度主要影響擾動振幅;粗糙元流向尺度通常影響擾動波頻率;粗糙元幾何形狀影響擾動波波形(二維或者三維)[80]。 近年來,隨著計算機硬件的飛速發展,針對粗糙元高超聲速感受性的數值模擬研究取得了較大進步。Wang、Zhong和Fong等[81-82]通過直接數值模擬(DNS)分析了孤立粗糙元高度對高超聲速邊界層感受性的影響。研究發現,孤立粗糙元的高度會使擾動瞬時增大,且增長率隨孤立粗糙元高度增加而變大。Duan等[83-84]也通過DNS方法研究了孤立粗糙元位置對高超聲速轉捩的影響,發現其位置的改變會直接影響慢模態在邊界層中的傳播,進而影響高超聲速邊界層的感受機理。在馬赫數5.92的來流條件下,Duan使用高階網格切割方法模擬了任意有限高度粗糙元和壁面抽吸對平板邊界層的組合影響,其中粗糙元高度為當地邊界層厚度的一半。圖14展示了慢模態和粗糙元引起的壓力波動,其中粗糙元放置于大約x=0.185m位置處。研究發現,流動經過邊界層后會出現明顯的壓力波動。此外,當粗糙元位于同步點上游時,不穩定波的發展和沒有粗糙元的情況相同;當粗糙元靠近同步點時,第二模態的不穩定性加劇;當粗糙元位于同步點下游附近,粗糙元會對不穩定的第二模態起到抑制作用。 圖14 慢模態和粗糙元引起的壓力波動[83] Fig.14PressureperturbationsinducedbymodeSandsurfaceroughness[83] 與單個孤立粗糙元相比,對離散式粗糙元的高超聲速邊界層感受性的研究要少很多。Duan和Zhong[85]將上述方法應用于來流馬赫數5.92條件下具有粗糙元陣列的三維平板邊界層轉捩的研究中。Balakumar[86]在尖錐模型上研究了二維離散式粗糙元對聲波的感受性,發現靠近前緣處的離散式粗糙元能夠降低慢聲波的感受性,且粗糙元后的邊界層比不帶粗糙元的光滑圓錐更穩定;這與Fong等[87]通過數值模擬得到的圓錐同步點后的粗糙元可以抑制Mack第二模態的結論相吻合。Balakumar將離散式粗糙元置于同步點附近,發現能夠提高Mack第二模態對渦波的感受性,但對快慢聲波的感受性則沒有影響。另外,粗糙元距離同步點的位置,以及粗糙元相對于當地邊界層厚度的比例,是影響感受性過程的重要因素。 一直以來,對邊界層轉捩的理論分析主要采用流動穩定性方法,即:考慮給定主流流動條件下的邊界層對外界擾動的感受性特征,主要研究不同種類的擾動在邊界層內的放大或衰減過程[88]。高超聲速三維邊界層內存在多種失穩機制[89]:附著線失穩、前緣污染失穩、第一和第二模態失穩、離心G?rtler渦失穩以及橫流失穩。橫流失穩屬于無粘條件下的不穩定性,是高超聲速飛行器表面三維邊界層轉捩的主導因素。 基于線性穩定性理論,橫流行波模態的放大率要高于橫流駐波模態。但是,由于橫流駐波模態對粗糙度有很強的感受性,這種感受性給橫流駐波模態提供了更高的初始振幅,彌補了其放大率的不足。因此,除了在來流擾動很強的條件下,橫流失穩中的主導不穩定模態都是橫流駐波模態[90]。在邊界層中,隨著橫流駐波模態的振幅增長,會形成同向旋轉的渦。這些旋渦和基本流的無粘流線近似重合,會對邊界層造成很強的綜合影響。隨著旋渦振幅進一步增大,會造成主流的扭曲,在主流速度型上形成拐點[91-94],如圖15所示[94]。帶有拐點的速度型會導致無粘二次不穩定性,產生小尺度的速度波動,使流動最終變成湍流。對可壓縮橫流失穩相關機理已有較多研究[95-99],本文主要介紹粗糙元在橫流失穩及控制中的研究工作。 圖15 橫流邊界層速度型[94] 粗糙元對橫流失穩的影響機理主要基于橫流駐波對表面粗糙度的強烈感受性[100]。Saric等[101]和Radeztsky等[102]利用這一特性,在后掠翼實驗中使用微米尺寸的圓形離散式粗糙元陣列,激發出具有固定展向波數的橫流駐波模態,并證實了在邊界層中只出現了相同展向波數的橫流模態(理論上,該波數的高次諧波也有可能出現,但低于該波數的橫流駐波模態總是被完全抑制)。這些觀測結果給出了粗糙元橫流控制的一種新思路,即:能否通過粗糙元激發出一種小振幅橫流駐波模態來控制轉捩。其關鍵是:引入的橫流駐波擾動模態的波數,要高于自然情況下主導轉捩的橫流駐波模態的波數,才能保證沒有擾動能量通過非線性相互作用進入到低波數、高放大率的擾動模態中。Saric等[101]通過實驗發現,使用高度為50μm的半球形點狀表面粗糙元能夠使后掠翼上的轉捩延遲。隨后,通過粗糙元、等離子體等對超臨界機翼的橫流失穩進行控制,發現粗糙元和等離子體可以改變基本流的形態,其激勵出的次不穩定橫流波可抑制先前最不穩定橫流波的發展,從而最終抑制橫流失穩[103]。 由于在高超聲速構型設計中能夠提供不同影響因素的豐富信息,圓錐被證明是研究高超聲速邊界層三維轉捩及橫流失穩問題的最理想外形[104]。因此,關于粗糙元對高超聲速橫流失穩影響的研究主要集中于帶迎角的圓錐。帶迎角的錐形流場會產生和流線垂直的壓力梯度,如果設計得當,該壓力梯度就會導致橫流的產生。Craig和Saric[105]對Ma=6來流條件下帶迎角圓錐的橫流失穩進行了研究,發現橫流駐波和行波模態的增長和發展與之前在低速實驗中觀察到的情況很一致。但是,當振幅飽和后,Ma=6來流條件下會觀測到二次不穩定波的發展,這種差異足以影響到最終的轉捩。因此,在高超聲速時,完全基于低速風洞實驗的橫流轉捩控制手段是無效的。 在Ma=3.5時,Schuele等[106]用半錐角為7°的圓錐進行了風洞實驗,并使用了離散式粗糙元,其激發出的次不穩定定常橫流渦使轉捩位置延遲了35%,如圖16所示(圖中m表示azimuthal wave number)。最近,Corke等[107]將Schuele的實驗擴展到了Ma=6來流條件,由于粗糙元引入了次不穩定擾動波,抑制了最不穩定擾動波的發展,因此轉捩延遲了25%。此外,由于Corke的實驗是在常規高超聲速風洞中進行的,實驗中觀測到了橫流駐波和行波之間的相互干擾,Corke推測這可能是常規高超聲速風洞中導致轉捩提前的原因。 圖16 不同粗糙元條件下的轉捩位置[106] Swanson等[108]對半錐角7°、迎角6°的圓錐在靜風洞中進行了來流馬赫數6的實驗。研究發現,在高噪聲來流中,轉捩趨向于背風面,通過在錐尖附近放置粗糙元可使轉捩前移。在低噪聲和靜來流中,采用溫度敏感漆(Temperature Sensitive Painting,TSP)均觀測到了橫流駐波,但沒有觀察到轉捩現象。在低噪聲條件下,粗糙元對駐波沒有產生明顯影響,增大風洞噪聲對駐波也沒有任何影響。van den Kroonenber等[109]使用相同的模型,利用紅外熱成像法獲得了圓錐全局傳熱的信息。研究發現,當單位雷諾數在6.5×106~11.3×106/m之間時,橫流駐波才能夠被觀測到。在圓錐尖端附近放置離散式粗糙元時,對駐波沒有明顯影響。在Mach 6靜風洞中,Chynoweth等[110]也利用TSP技術對粗糙元控制尖錐的橫流失穩現象進行了研究,結果如圖17所示。可以看出,在低單位雷諾數條件下(8.1×106/m),粗糙元會引起較大振幅的橫流駐波(與光滑壁面相比),從而促進邊界層橫流失穩;而在較高單位雷諾數條件下(10.4×106/m),則會引起較小振幅的橫流駐波,從而抑制邊界層不穩定性。目前,對這一現象還沒有清晰的解釋。 圖17 不同單位雷諾數對粗糙元抑制轉捩的影響[110] Fig.17EffectofReynoldsnumberonsuppressingtransitionbyroughnesselements[110] 目前,已有多種新興測量技術應用于高超聲速轉捩研究[111-113],如PIV、PLIF、NPLS等。雖然它們的測量精度較高,但是均存在近壁剪切力大、粒子均勻播散困難、校準和實驗方法復雜等問題。油膜干涉法是一種適用于邊界層轉捩風洞實驗的傳統的非接觸測量方法。該方法具有測量面積大、測量精度高和實驗成本低等特點[114-116]。近年來,本文作者將油膜干涉法應用于邊界層轉捩風洞實驗研究,在低速風洞[117-118]、高速風洞[119-121]中取得了一定成果,在南京航空航天大學高超聲速風洞(NHW)中也開展了三維表面凸起粗糙元誘導高超聲速平板邊界層轉捩的實驗研究。 NHW是一座噴管出口直徑Φ500mm的高壓下吹、真空抽吸暫沖式高超聲速風洞,實驗名義馬赫數為4、5、6、7和8,真空球容積為650m3,每車次實驗時間可大于10s[122]。試驗段及真空駐室上方有一個350mm×350mm的觀察窗,可通過觀察窗使用CCD相機或高速攝像機對模型和流場進行相關光學測量。 在高超聲速邊界層轉捩風洞實驗研究中,來流噪聲水平一直是一個重要的參數。目前的主流研究設備分兩種,第一種是高超聲速靜風洞(如普渡大學Mach 6靜風洞、北京大學Mach 6靜風洞、國防科技大學Mach 3~6低噪聲風洞),通過一系列降噪措施(如拋光壁面、抽吸等),使來流噪聲水平低于0.1%(來流壓力脈動/平均壓力)。但靜風洞建造成本高、來流馬赫數一般有限制,難以大規模推廣。第二種是傳統高超聲速風洞,其來流噪聲水平一般要比高超聲速靜風洞高一個量級(具體數值與來流總壓、來流馬赫數、測量位置等參數密切相關)。本文涉及的南京航空航天大學NHW風洞實驗均為高超聲速轉捩數值方法和實驗技術的驗證性實驗,并未實時監測來流噪聲水平。根據實驗來流參數,由文獻[123]可知,在來流總壓約4×105Pa、名義馬赫數5的條件下,NHW風洞的噪聲水平低于2.5%。 其他實驗設備包括單色光源、高速相機以及分析純度硅油。其中,單色光源采用單色鈉燈和單色LED燈,波長均為589nm;相機為PCO公司的S4高速相機,實驗幀率為100幀/s(遠低于其極限幀率1000幀/s);硅油選用阿拉丁公司的粘度為50cst的高純度分析級硅油。 油膜干涉實驗模型為平板模型,長190mm,寬150mm,前緣為倒角20°的尖楔形。三維粗糙元為圓柱形孤立粗糙元,直徑3mm,高度1.6mm,距離模型前緣50mm,中心位于平板模型沿流向的對稱面上。 實驗名義馬赫數為5,來流馬赫數為4.97,來流總壓p0=3.909×105Pa,總溫T0=516K,單位雷諾數為4.7×106/m。在進行模型表面尺寸標定后進行風洞實驗,測量范圍為距離平板前緣約50~130mm的局部區域。為比對驗證實驗結果,采用基于有限體積的高階緊致格式(CFVM)并行算法[124],對相同來流條件下的光滑平板模型以及帶三維圓柱形孤立粗糙元的平板模型進行數值模擬。 圖18為風洞流場中光滑平板模型油膜干涉圖像,以及由此計算出的沿流向中心線上相應位置的表面摩擦阻力系數Cf和數值模擬結果的比較。可以看出:硅油在剪切力作用下向下游延展,形成硅油薄膜,經單色鈉光照射,產生清晰的干涉條紋;模型表面中心線處的摩阻系數Cf沿流向逐漸減小,且風洞實驗結果與層流數值模擬結果吻合;Cf數值約為0.001,表明當前平板邊界層流動處于層流流態,在可視范圍內沒有發生自然轉捩。 圖19為風洞流場中帶三維圓柱形孤立粗糙元的平板模型油膜干涉條紋,以及數值模擬得到的Cf分布和對稱面上密度分布圖。對比圖18可見,三維圓柱形孤立粗糙元后的干涉條紋比光滑平板模型的寬得多。由密度分布圖可知,這是由于三維粗糙元后方流場中形成了尾渦,引起平板邊界層中強烈的擾動和剪切作用,使層流邊界層轉捩為湍流。由數值計算結果可知,粗糙元對下游邊界層流場的影響程度以x=100mm為界線分為兩個部分:在x=100mm之前,粗糙元后中心線上下有兩個對稱區域A和B,該區域Cf較大(比相同x位置的中心線上的Cf更大),這與油膜干涉圖像中的1、2、3區域相吻合;在x=100mm之后,中心線上下兩側區域的Cf逐漸減小,這與油膜干涉圖像中展向條紋連續性變得更好的趨勢相吻合。 (a) Ma=5條件下光滑平板表面油膜干涉條紋圖像 (b) 表面摩擦阻力系數實驗結果和數值結果對比 Fig.18Oilfilminterferenceimageofsmoothflatplateandcomparisonofsurfaceskinfrictioncoefficient (a) Ma=5條件下粗糙元尾跡區油膜干涉條紋 (b) Ma=5條件下基于DNS的粗糙元尾跡區摩擦阻力系數分布 (c) Ma=5條件下基于DNS的粗糙元中心剖面密度分布 Fig.19Oilfilminterferencefringesandnumericalsimulationresultsafter3Dcylindricalisolatedroughnesselements 以上研究表明,油膜干涉測量技術可以應用于粗糙元誘導高超聲速邊界層轉捩的研究中。下一步,可結合NHW噪聲水平的實時監測,對不同形狀、不同高度、不同間距等的離散式粗糙元誘導轉捩的效果和機理進行深入研究。 國防和民用航空航天領域對高超聲速飛行器及高超聲速技術發展需求日益強烈,對高超聲速邊界層轉捩問題的研究也更加迫切。但轉捩問題的復雜性、研究手段的局限性以及現有理論的不完善,決定了轉捩研究將是一個長期而艱難的過程。在這一過程中,轉捩機理是研究的重點、難點和根本;而轉捩預測和轉捩控制方法是研究的主要目的,直接支撐著新型高超聲速飛行器的研制。作為影響高超聲速邊界層轉捩的諸多因素之一,粗糙元是轉捩控制的主要手段,必將長期作為研究熱點。 現有研究表明,精心設計的離散式粗糙元可以推遲轉捩。研究者不僅應繼續注重規則粗糙元高度/深度、形狀等參數對誘導轉捩效果及機理的相關研究,更應重視離散式粗糙元間距、不規則粗糙元等對高超聲速轉捩的影響。另外,對燒蝕、物理損傷、機械加工等造成的飛行器表面不規則的凸起或凹陷的研究,更加具有工程價值。 粗糙元影響高超聲速邊界層轉捩機理的研究已取得了一定成果。大多數研究者認為:粗糙元會在高超聲速邊界層內產生具有流向渦度的尾渦,足夠高度的粗糙元將產生激波,尾渦和激波的作用會增加邊界層內的不穩定性。一方面,邊界層內的粘性效應不足以使這種不穩定性在流動下游消散;另一方面,隨粗糙元參數變化的流向渦會通過與自由流擾動的相互作用(感受性)、橫流失穩、G?rtler失穩以及瞬態增長機制而發展,最終導致層流轉捩為湍流。目前,對高超聲速邊界層感受性、橫流失穩的研究很少[8]。在感受性問題中,要注重針對粗糙元誘導的不穩定波激發路徑的理論和實驗研究;而在橫流失穩中,應重點關注三維邊界層中諸如駐波、行波、二次失穩、第二模態等多種擾動模態的辨識和相互干擾問題。 高超聲速流動存在區別于低速、一般超聲速的明顯特征,在低速或一般超聲速邊界層轉捩中出現的現象或適用的規律,在高超聲速條件下并不存在或不適用。有研究表明,在低速、一般超聲速中應用的轉捩控制手段,在高超聲速條件下并不完全有效。但是,不能將高超聲速邊界層轉捩的研究局限于高超聲速范圍之內,使之與低速、一般超聲速流動中的轉捩研究割裂開來。這是由于高超聲速飛行器近壁面邊界層、駐點附近的馬赫數很低,將粗糙元布置在這些位置,控制效果更加明顯。例如,航天飛機和高超聲速導彈鼻錐處粗糙元后的流動,也屬于高超聲速轉捩研究的內容,具有重要的研究價值。 總而言之,高超粗糙元形式眾多,本文僅簡要綜述了表面凸起、凹腔、多孔壁面、分布式粗糙度的相關研究。各種粗糙元對高超聲速邊界層轉捩影響的機理和規律尚不完全清楚,需要通過理論、數值方法以及高超聲速風洞實驗技術的發展和進步,并與飛行試驗數據驗證相結合,循序漸進地開展更加深入的研究。

1.3 不規則分布式粗糙度對高超聲速轉捩影響研究


2 轉捩機理研究
2.1 感受性
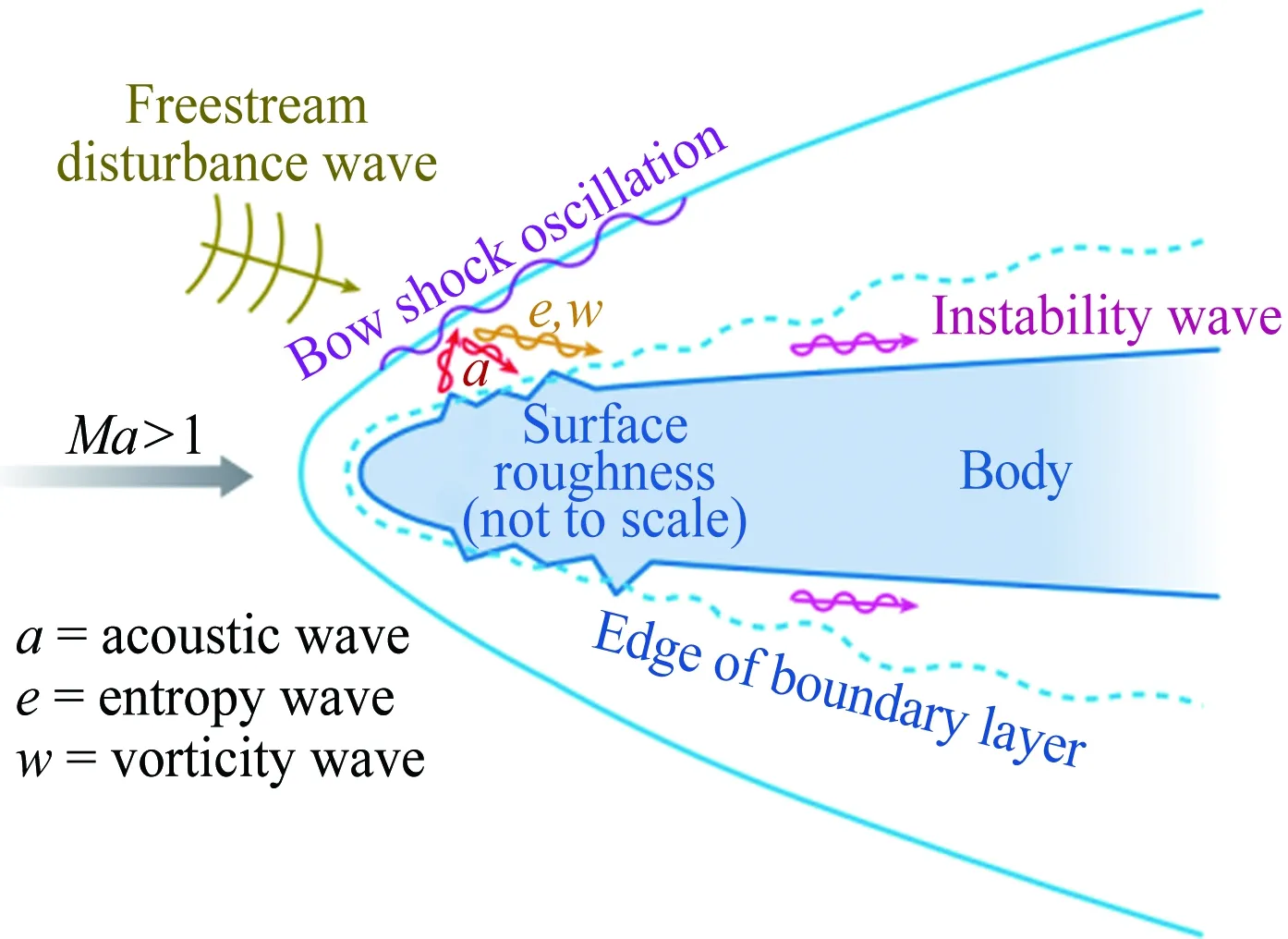
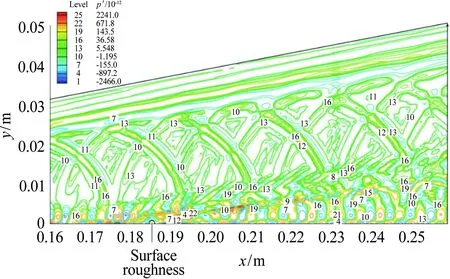
2.2 橫流失穩
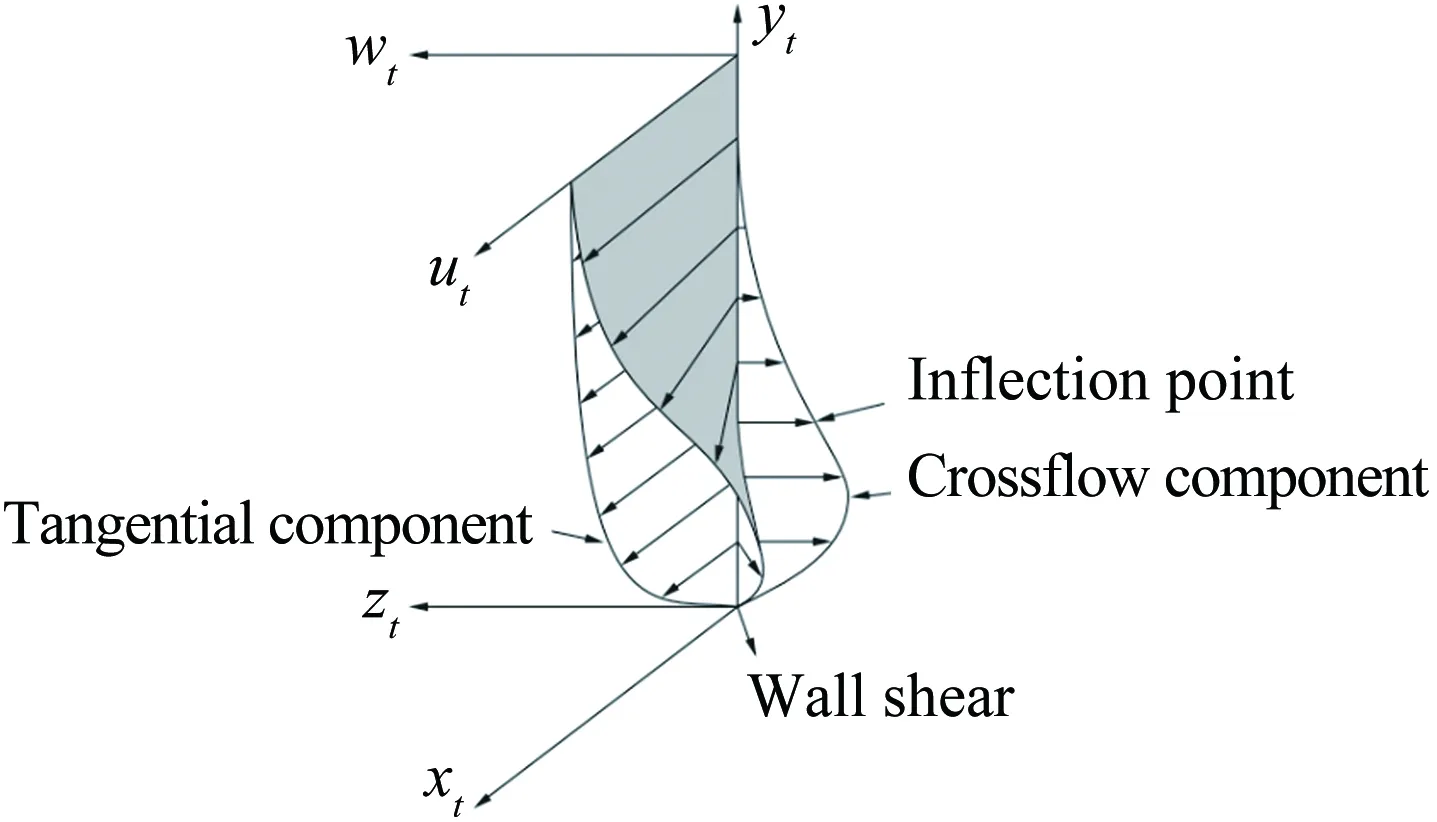
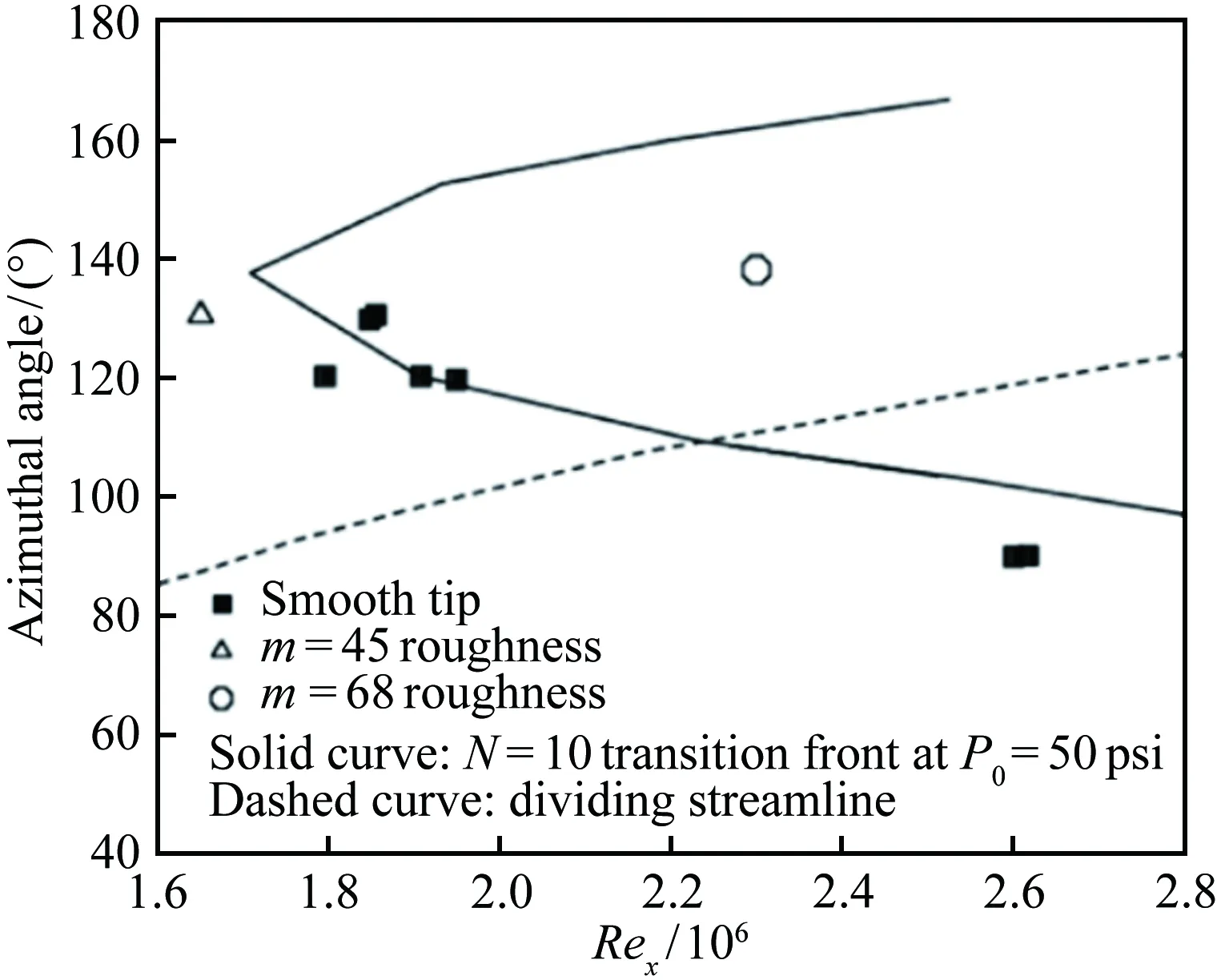
3 NHW風洞相關研究進展
3.1 實驗設備及模型
3.2 實驗結果及分析


4 結束語

