基于Ansys有限元軟件的鋼箱梁人行天橋主梁結構安全驗算實例分析
趙海艷


摘要:通過對某鋼箱梁人行天橋為研究對象,運用橋梁博士V3.5.0軟件及Ansys有限元軟件,對鋼箱梁人行天橋主梁結構的強度、穩定性、撓度及自振頻率進行了驗算,為類似鋼結構人行天橋的結構設計與計算提供依據。
關鍵詞:鋼箱梁;人行天橋;穩定性;自振頻率;有限元
中圖分類號:S611? 文獻標識碼:A? 文章編號:1007-9416(2018)10-0000-00
1 引言
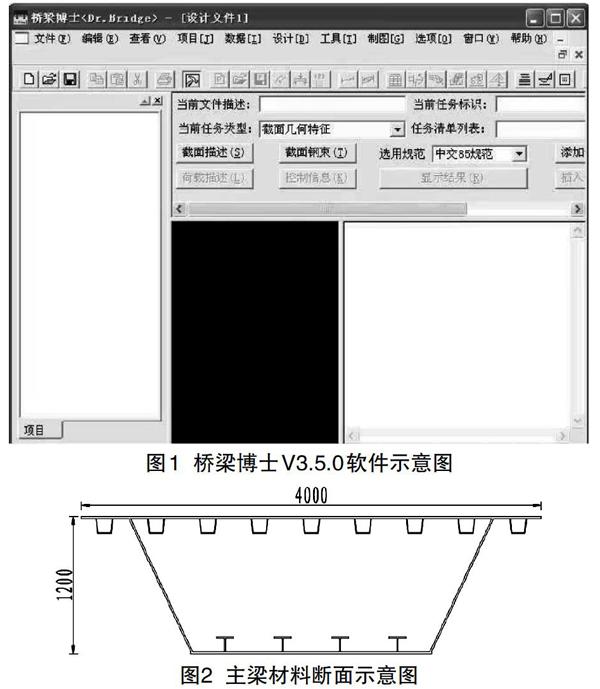
隨著城市發展進程的加速,城市交通日趨飽和,交通壓力逐漸增大,為提高城市路網的通行能力、確保過街行人的安全和城市交通的順暢通行,人行天橋的建設對車輛運行速度的提高、交通擁擠狀況的改善、實現人車的分流等起著至關重要的作用。諸多學者對其進行了大量的研究,目前的研究主要圍繞結構振動與穩定性方面開展,尹越應用有限元分析手段對不同質量的車輛撞擊鋼結構人行天橋的鋼柱柱進行了分析、李強通過振動測試分析結合舒適度進行人行天橋綜合評價。王力彬以西藏林廓天橋項目為背景,分析了TMD對行人過街天橋的振動控制。本文以某兩跨鋼箱梁人行天橋為例,在組合荷載作用下,運用橋梁博士及ANSYS有限元模型對人行天橋主梁結構的強度、撓度、自振頻率及穩定性進行驗算,并對其安全性指標進行了分析。橋梁博士V3.5.0軟件如下圖1所示。
2 工程介紹與設計標準
本文分析的人行天橋主體結構為鋼結構。主橋跨度采用(37+27)m,單箱單室,橋面全寬4.0m,人行道凈寬3.5m,兩側設置欄桿寬為0.25m。主梁高度為1.2m。橋下車道最小凈空為5.0m,主橋雙向橫坡為1%,縱坡為0.3%,安全等級為一級。
本文分析的天橋主要荷載設計標準為|:鋼材的容重為78.5KN/m3,人群荷載按照規范《城市人行天橋與人行地道技術規范》(CJJ69-95)取值, 主梁材料采用Q345D鋼板焊接而成,主梁工廠分段制造,工地安裝焊為一體。
具體斷面如圖2所示。
3 上部結構主梁計算分析
3.1 基本假定
(1)材料在荷載作用下處于小變形和線彈性階段;
(2)各種荷載對結構的作用符合線行疊加原理的條件。
3.2 上部結構箱梁承載能力驗算
有限元模型的建立:利用橋梁博士V3.5.0軟件建立該橋上部結構模型,共分為梁單元64個,節點65個,如圖3所示。
3.3 材料參數及荷載效應值
模型所選用的材料與實際橋梁一致,主梁材料采用Q345D鋼板焊接而成,主梁工廠分段制造,工地安裝焊為一體,鋼板的彈性模量為2.06x105,容重為78.5KN/103。主橋一期橫載為鋼箱梁自重,二期橫載由橋面鋪裝、欄桿等自重構成,橋面鋪裝15.6KN /m,欄桿15.0 KN /m,人群荷載取3.5KN/m。
根據《鋼結構荷載規范》(GB50017-2003)第3.2.1條,依據《建筑結構荷載規范》(GB50009-2012)第3.2條進行荷載組合進行驗算。
3.3.1 強度與撓度
按照根據《鋼結構荷載規范》(GB50017-2003)第3.2.1條,按照《建筑結構荷載規范》(GB50009-2012)第3.2條荷載組合下計算,按照規范要求的鋼材允許正應力210MPa,使用階段鋼板最大拉應力為59.91MPa<210MPa,最大拉應力滿足規范要求;使用階段鋼板最大壓應力為35.75MPa<210MPa,滿足規范要求。
小箱梁結構跨中部位結構重力產生的撓度為2.12cm,人群荷載產生的最大撓度為2.0cm。人群荷載產生的撓度小于L/600,結構自重+人群荷載跨中產生的最大撓度為4.12cm,大于L/1600=2.18cm,滿足使用要求。
3.3.2 自振頻率和穩定性
根據《城市人行天橋與人行地道技術規范》(CJJ69-95)的相關規定,人行天橋的自振頻率不應小于3Hz。同時本橋橋面寬度較窄,需要用空間程序進行穩定計算。所以用大型通用有限元程序ansys建立模型,進行自振頻率和穩定計算。
根據本橋的特點,鋼板采用板殼單元(shell64)進行模擬,全橋劃分為28830個單元,26124個節點,全橋結構的計算模型如圖4所示。
經過用ansys進行模態分析,得出全橋前十階自振頻率如下:
SET? ?TIME/FREQ? ? LOAD STEP? ?SUBSTEP? CUMULATIVE
1? 3.4896? ? ? ? ? ? ?1? ? ? ? ?1? ? ? ? ?1
2? 4.5834? ? ? ? ? ? ?1? ? ? ? ?2? ? ? ? ?2
3? 5.6657? ? ? ? ? ? ?1? ? ? ? ?3? ? ? ? ?3
4? 5.9744? ? ? ? ? ? ?1? ? ? ? ?4? ? ? ? ?4
5? 6.0703? ? ? ? ? ? ?1? ? ? ? ?5? ? ? ? ?5
6? 6.8936? ? ? ? ? ? ?1? ? ? ? ?6? ? ? ? ?6
7? 7.2555? ? ? ? ? ? ?1? ? ? ? ?7? ? ? ? ?7
8? 7.3686? ? ? ? ? ? ?1? ? ? ? ?8? ? ? ? ?8
9? 7.9804? ? ? ? ? ? ?1? ? ? ? ?9? ? ? ? ?9
10? 8.4118? ? ? ? ? ? ?1? ? ? ? ?10? ? ? ? 10
從以上計算結果可知,一階自振頻率為3.4896Hz,滿足規范要求,如圖5所示。
經過用ansys進行屈曲分析,得出全橋前十階穩定系數如下:
SET? ?TIME/FREQ? ? LOAD STEP? ?SUBSTEP? CUMULATIVE
1? 4.9773? ? ? ? ? ? ?1? ? ? ? ?1? ? ? ? ?1
2? 5.2464? ? ? ? ? ? ?1? ? ? ? ?2? ? ? ? ?2
3? 6.0312? ? ? ? ? ? ?1? ? ? ? ?3? ? ? ? ?3
4? 6.1451? ? ? ? ? ? ?1? ? ? ? ?4? ? ? ? ?4
5? 6.9583? ? ? ? ? ? ?1? ? ? ? ?5? ? ? ? ?5
6? 6.9800? ? ? ? ? ? ?1? ? ? ? ?6? ? ? ? ?6
7? 8.0867? ? ? ? ? ? ?1? ? ? ? ?7? ? ? ? ?7
8? 8.7799? ? ? ? ? ? ?1? ? ? ? ?8? ? ? ? ?8
9? 8.9355? ? ? ? ? ? ?1? ? ? ? ?9? ? ? ? ?9
10? 9.3883? ? ? ? ? ? ?1? ? ? ? 10? ? ? ? 10
一階失穩如圖6所示。
從以上計算結果可知,一階失穩系數為4.9773,達到使用需求。
4 結語
本文通過一實例鋼箱梁人行天橋進行驗算和分析,其現有設計滿足規范要求,通過驗算得到如下結論:
(1)本文通過運用橋梁博士V3.5.0軟件及ansys有限元軟件,在相應荷載組合下,對鋼箱梁人行天橋主梁結構的強度、穩定性、撓度及自振頻率進行了驗算,驗算結果滿足規范要求,本鋼箱梁人行天橋安全可靠。
(2)通過對該鋼箱梁的計算,能夠為類似鋼結構人行天橋的結構設計與計算提供依據。
參考文獻
[1]袁騰文.鋼箱梁人行天橋承載力檢算實例分析[J].公路與汽運,2018,(02):141-143,148.
[2]趙磊.鋼結構人行天橋結構設計簡明計算全過程分析[J].山西交通科技,2015,(01):51-54.
[3]舒琳智.城市鋼箱梁人行天橋結構計算分析研究[D].西南交通大學,2013.
[4]《公路橋涵設計通用規范》(JTGD60_2004).
[5]《公路橋涵地基與基礎設計規范》(JTGD63-2007).
[6]《公路橋梁抗震設計細則》(JTG/TB02-01-2008).
[7]《城市人行天橋與人行地道技術規范》(JJ69-95).
[8]《建筑鋼結構焊接規程》(JGJ81-2002).
[9]饒志堅.人行天橋動力建模與減振控制[D].華中科技大學,2008.
[10]張金富.無錫市太湖大道人行天橋設計[J].中國市政工程,2007(S2):20-22,26.
Analysis of Examples of Safety Checking of Main Girder Structure of Steel Box Girder Pedestrian Bridge Based on ANSYS Finite Element Software
ZHAO Hai-yan
(China Railway Construction Suzhou Design and Research Institute Co., Ltd., Suzhou Jiangsu 215104)
Abstract: Based on a steel box girder pedestrian bridge as the research object, the strength, stability, deflection and natural frequency of the main girder structure of the steel box girder pedestrian bridge are checked by using the software of Dr. Bridge V3.5.0 and Ansys finite element software, which provides a basis for the structural design and calculation of similar steel structure pedestrian bridge.
Key words: Steel box girder; pedestrian overpass; stability; natural frequency; finite element method

