六自由度搖擺臺反解建模與仿真

梁東生,王利娟,馮兆緣

(1.江蘇科技大學 鎮江四洋柴油機制造有限公司, 鎮江 212003) (2.江蘇科技大學 能源與動力工程學院, 鎮江 212003)

英國學者Stewart于1965年提出了六自由度并聯運動平臺的典型機構—Stewart,經過50余年的發展,該平臺己成為涉及機械工程、計算機科學、軟件工程、控制工程和系統仿真等多學科領域的系統集成技術[1-4]，在柔性制造,運動空間姿態模擬等領域發揮了越來越顯著的作用，并由此發展出并聯機構理論.由于并聯平臺比串聯平臺更具有剛度大、穩定性好、承載能力強等優點,因此，其在機器人執行器、運動模擬器、并聯機床等領域得到了廣泛應用[5-8]．

文獻[9]基于反解算法利用MATLAB構建了6-DOF的仿真平臺，并對運動平臺6個作動器的位移、速度等進行計算;文獻[10]在 MATLAB中利用 xPC Target 技術和模塊編程的思想對6-DOF進行正解和反解，但文獻[9-10]的算法均過于復雜,控制成本較高,且仿真輸入數據均未與實驗數據進行比較，無法驗證其算法的準確性．文獻[6]建立并聯6-DOF平臺控制系統的數據通信通道,將海浪視覺模擬系統與并聯六自由度平臺控制系統聯系起來，該方法為在MATLAB/Simulink建立的仿真系統的數據通信提供了良好的基礎．文中以液壓六自由度并聯搖擺實驗臺為研究對象,推導6-DOF平臺位姿的反解方程,利用MATLAB/Simulink搭建了反解模型,分析平臺在6個自由度上的運動規律,為進一步開發平臺的控制器,制定可靠的策略奠定了基礎．

1 6-DOF平臺反解模型的構建

1.1 6-DOF平臺

6-DOF平臺主要包括:上平臺、下平臺(固定)、6個液壓缸、電液伺服閥、12個球鉸等關鍵部件．其中,液壓缸通過球鉸以并聯方式將上下平臺連接成一柔性系統,通過6個液壓缸的協同運動,實現上平臺在空間6個自由度方向上的姿態變化[11-13]．文中研究的實驗室液壓6-DOF平臺主要用于模擬器在顛簸路面或海面上波浪作用下的搖擺姿態模擬,檢驗所模擬的駕駛模擬器運動運行的狀態，液壓6-DOF并聯搖擺實驗臺如圖1．

圖1 液壓6-DOF并聯搖擺實驗臺Fig.1 Hydraulic 6-DOF parallel swing test bench

1.2 6-DOF平臺坐標體系的建立及變換

采用坐標變換的方式對6-DOF平臺的動平臺(上平臺)進行位置分析,其方法為:

(1) 在靜平臺(下平臺)上建立笛卡爾靜坐標系O-XYZ,坐標系原點O與靜定平臺上各驅動桿鉸接點所在圓面的圓心重合．

(2) 在動平臺上建立動坐標系O′-X′Y′Z′,坐標原點O′與上平臺各驅動桿鉸接點所在圓面的圓心重合．當6-DOF平臺處于初始狀態時,上述兩個坐標系的X、Y、Z軸的方向一致,Z-Z′軸重合,X-X′與Y-Y′相互平行,如圖2．由Z軸方向投影,可得到上、下平臺鉸鏈點的分布,如圖3．

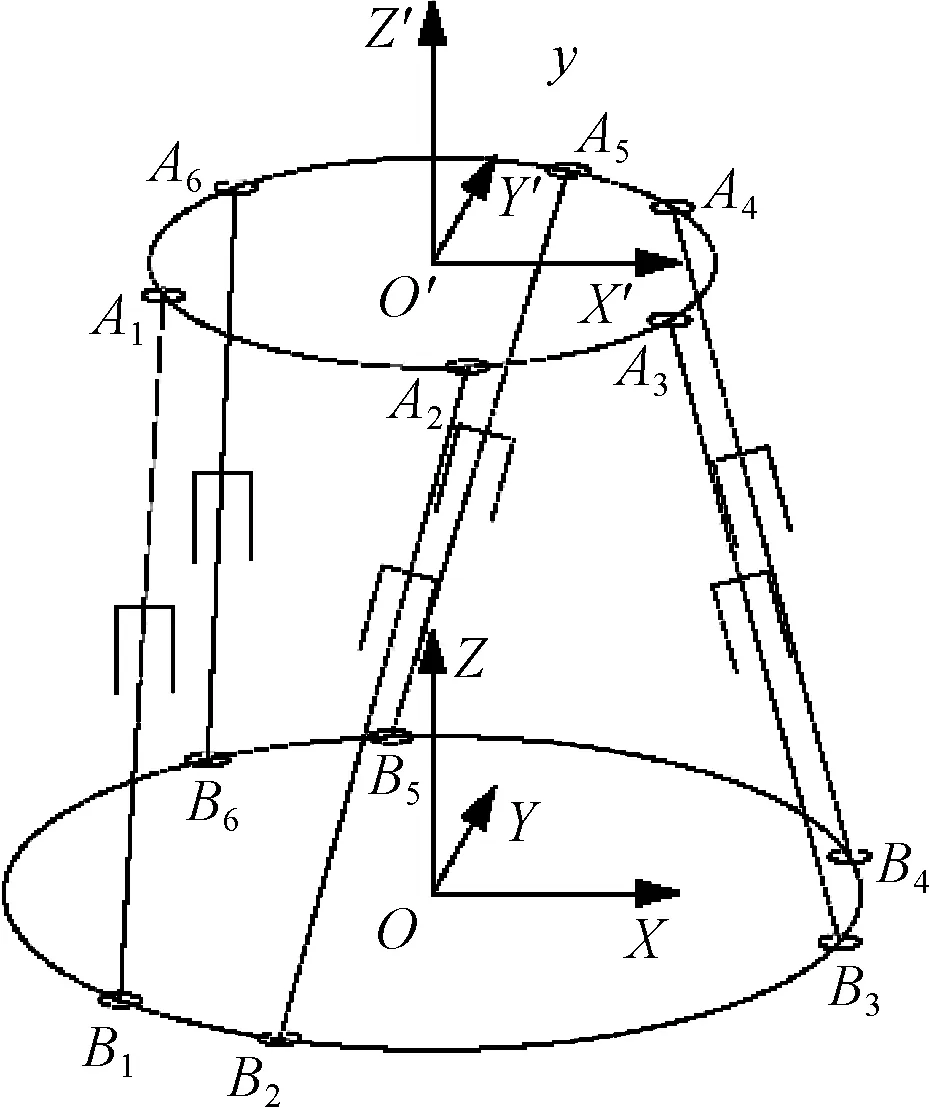
圖2 平臺坐標系Fig.2 Platform coordinate system

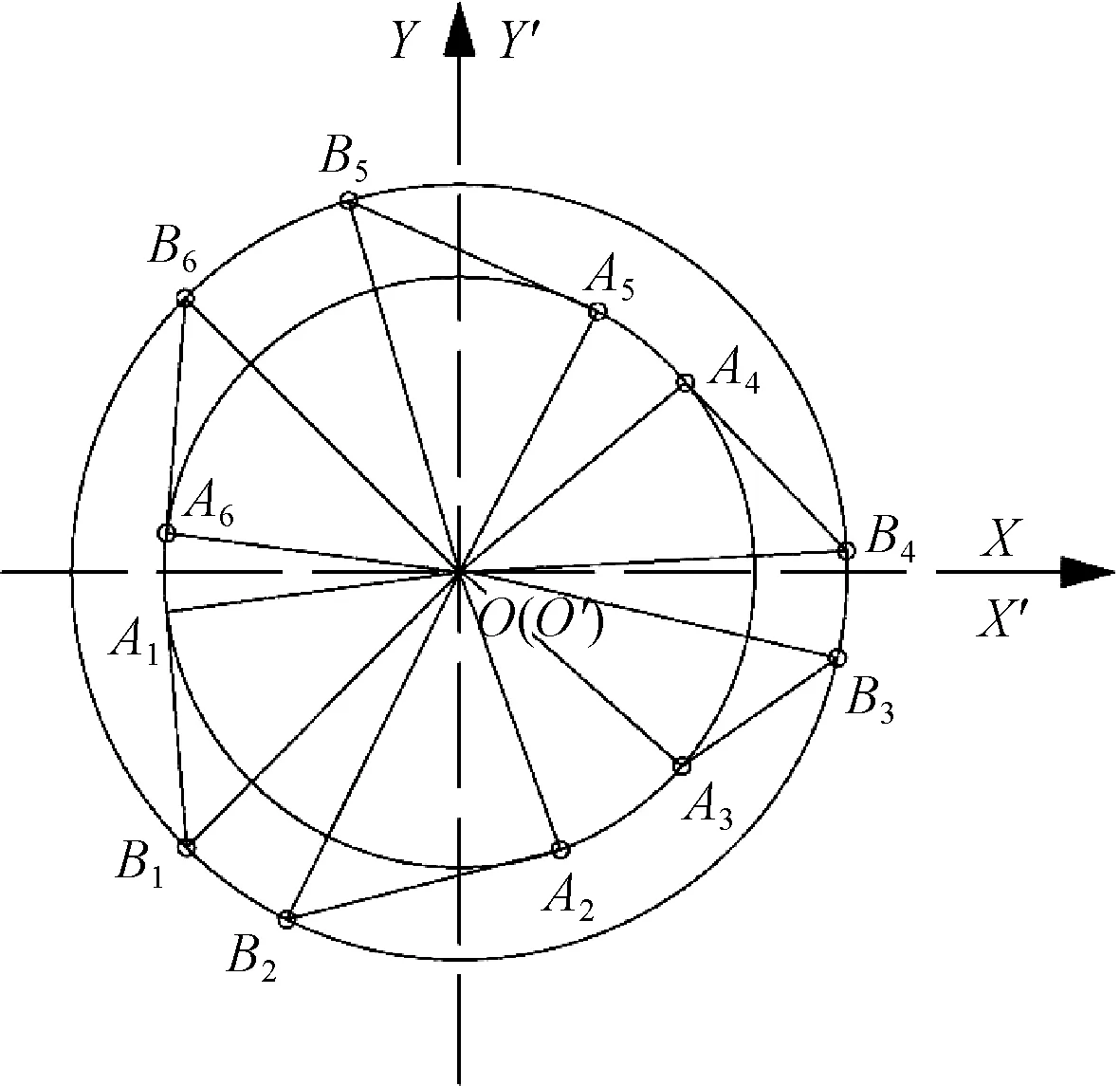
圖3 上、下平臺鉸鏈點Fig.3 Upper and lower platform hinge points

6-DOF平臺的參數如表1．

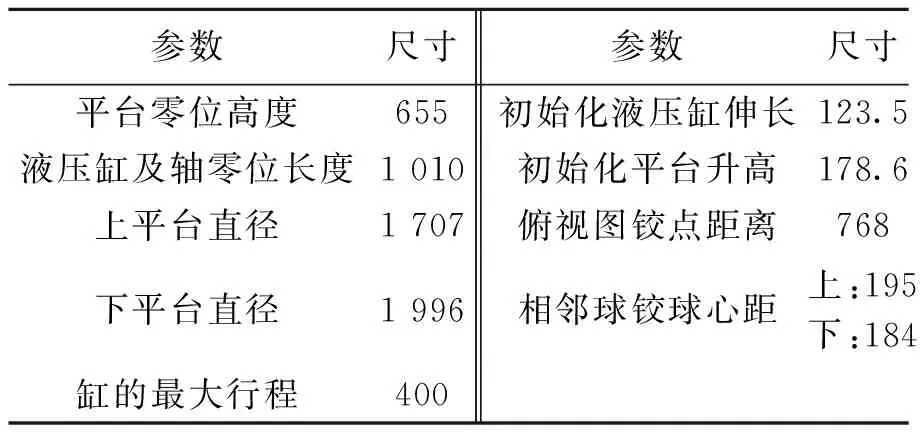
表1 6-DOF平臺參數

將6-DOF平臺參數代入圖2的平臺坐標系中，得到平臺處于零位狀態時各鉸點的坐標,如表2．

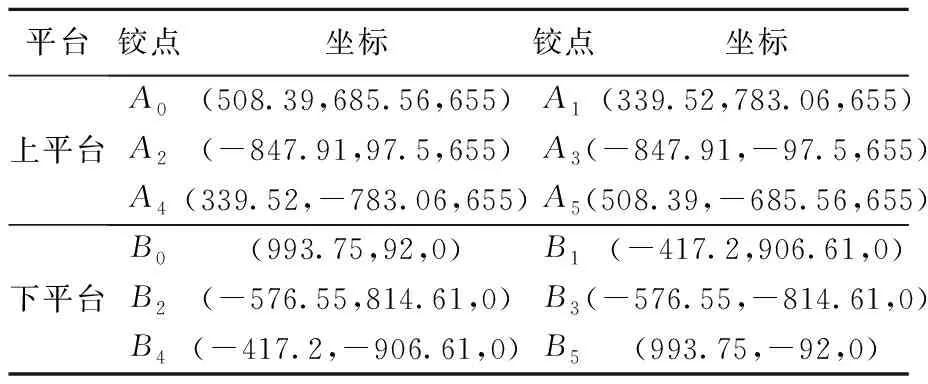
表2 上、下平臺各鉸點零位坐標

由6-DOF平臺中上平臺在空間中的姿態可求各液壓缸的伸縮長度,即位置反解．對其進行反解,將動坐標系中鉸鏈點的坐標向量變換到靜坐標系中,再將變換得到的向量與靜坐標系中鉸鏈點的坐標向量相減得到液壓缸的缸長矢量,從而求出缸長[14-15]．

采用歐拉角方式來描述動坐標系在靜態坐標系中的姿態,對6-DOF平臺運動姿態分析,通過3次平移變換,將靜坐標系分別沿著X軸、Y軸、Z軸進行平移運動；再進行3次旋轉變換,即沿X軸、Y軸、Z軸旋轉．通過以上過程,可得到由靜坐標系到動坐標系的坐標變換矩陣T=

(1)

1.3 6-DOF平臺位置反解

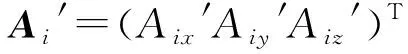
當平臺動作時,上下相應鉸支點間距離li的計算公式為:

(i=1,2,…,6)

(2)

Δli=li-l0

(3)

式中：Δli為液壓缸缸長的伸縮量,l0為液壓缸的初始長度.

2 6-DOF的運動學反解仿真

利用MATLAB中的Simulink模塊建立了6-DOF平臺反解仿真模型,如圖4．模型包括期望信號輸入模塊、液壓缸缸長反解算法模塊、信號輸出模塊．將文中所提的6-DOF液壓缸缸長反解算法以MATLAB Function模塊寫入整個仿真模型中,得到各液壓缸的長度變化規律．

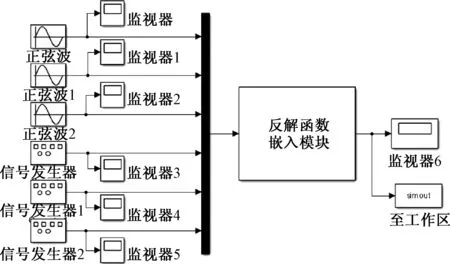
圖4 6-DOF臺運動學反解Simulink仿真模型Fig.4 Kinematics inverse solution of 6-DOFSimulink simulation model

讓6-DOF平臺分別仿真沿X軸平移、沿Y軸平移、沿Z軸平移、繞Z軸旋轉運動,其中平移幅值為100 mm,頻率為1 Hz,轉動的幅值為π/6, 頻率為1 Hz．通過反解算法模塊得到6個液壓缸缸長變化規律,用示波器Scope 模塊,將缸長變化量以圖像的形式輸出．仿真時6個自由度的運動均為正弦運動,仿真結果見圖5,圖中曲線1～6代表1～6號液壓缸．

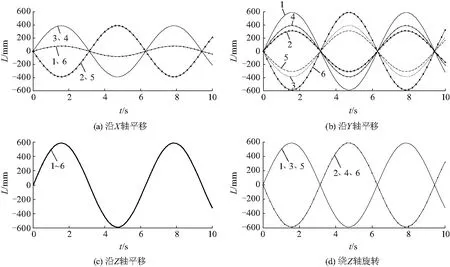
圖5 液壓缸長度變化曲線Fig.5 Hydraulic cylinder length variation

圖5直觀地反映了6-DOF平臺位姿變化時,6個液壓缸缸長變化規律．所建仿真模型簡單方便,為進一步研究6-DOF平臺并能更好地完善其控制策略奠定基礎．

將實驗室中6-DOF并聯搖擺實驗臺沿X軸的平移運動,得到各液壓缸缸長實際值如圖6，驗證所建6-DOF平臺反解算法及所建仿真模型的正確性．

圖6 沿X軸平移時液壓缸缸長實際值Fig.6 Actual cylinder length when movingalong the X-axis

3 結論

(1) 通過建立6-DOF平臺坐標及其換體系,推導6-DOF平臺的反解算法,利用MATLAB中Simulink模塊建立了6-DOF平臺的仿真系統,直觀地得到了各液壓缸缸長變化規律,反解算法簡便,仿真系統簡單高效．

(2) 采用6-DOF平臺仿真系統與試驗臺研究姿態變化運動,得到各液壓缸缸長變化規律,驗證反解算法及仿真模型的正確性,6-DOF平臺的運動規律,為下一步深入研究6-DOF平臺運動特性及其控制系統打下良好的基礎．