電力系統(tǒng)低頻振蕩在線辨識算法研究

劉曉菊，趙周芳，趙 瑩，劉瑞花

（國網(wǎng)四川省電力公司技能培訓中心（四川電力職業(yè)技術(shù)學院），四川 成都 611133）

0 引 言

隨著電網(wǎng)互聯(lián)規(guī)模的不斷擴大和國民經(jīng)濟水平的日益提高，人們對供電可靠性和穩(wěn)定性提出了更高要求。而快速、高放大倍數(shù)勵磁系統(tǒng)的廣泛應(yīng)用，使電力系統(tǒng)低頻振蕩問題威脅電網(wǎng)的安全、穩(wěn)定運行[1-2]。可通過采取措施消除低頻振蕩[3]，但準確、有效提取低頻振蕩模態(tài)參數(shù)卻十分困難。人們習慣采用小信號穩(wěn)定分析、線性化處理等方法研究低頻振蕩問題，并取得了一定成果。但是，隨著系統(tǒng)規(guī)模的擴大和復雜程度的增加，線性化方法的不足日益突出。因此，Prony算法和HHT算法應(yīng)運而生。目前，Prony算法已在電力系統(tǒng)低頻振蕩分析中獲得廣泛應(yīng)用，但還存在諸多不足。比如，不能有效抑制噪聲、不能準確辨識系統(tǒng)的實際階數(shù)、擬合非平穩(wěn)信號的效果不理想等，且近年來提出的一些改進算法都需要濾波或去直等數(shù)據(jù)預(yù)處理[4-5]。希爾伯特-黃變換（HHT）算法能有效分析非線性、非平穩(wěn)信號，克服了小信號穩(wěn)定分析、線性化處理及Prony方法的不足，同時可實現(xiàn)對數(shù)據(jù)的去直和濾波處理[6]。

1 Prony算法和HHT算法介紹

根據(jù)Prony算法，一組等間隔采樣數(shù)據(jù)x(1)…x(N)可以用x個具有任意幅值、相位、頻率和衰減因子的指數(shù)函數(shù)的線性組合擬合。

Prony算法一般將信噪比SNR作為擬合指標。當SNR大于40 dB時，擬合結(jié)果在可接受范圍之內(nèi)。用Prony算法擬合數(shù)據(jù)要選取適當?shù)牟蓸宇l率和采樣時間。選取不同的模型階數(shù)，擬合效果可能不同。階數(shù)過低，會丟失重要數(shù)據(jù)，擬合指標降低，從而不能成功擬合實際系統(tǒng)；過高的模型階數(shù)則會增加計算量，產(chǎn)生大量冗余項。因此，模型階數(shù)的選取成為Prony算法的一大難題。

HHT算法假設(shè)任何信號都可以分解成若干個不同的固有模態(tài)函數(shù)，每個模態(tài)函數(shù)可以是線性的，也可以是非線性的。它由經(jīng)驗?zāi)B(tài)分解（Empirical Mode DecomPosition，EMD）及Hilbert變換（HHT）組成，其中EMD分解是核心部分。HHT算法由EMD分解完成數(shù)據(jù)的線性化和平穩(wěn)化，進而得到能反映原始信號局部特征的IMF（Intrinsic Mode Function）分量，再用Hilbert變換轉(zhuǎn)變IMF分量得到瞬時頻率及瞬時振幅，最后實現(xiàn)信號的時頻分析。其中，IMF分量具有以下特點。

（1）滿足N1=N2或|N1-N2|=1，其中N1為IMF分量極值點的數(shù)目，N2為IMF分量過零點的數(shù)目。

（2）局部極大值形成的包絡(luò)線和局部極小值形成的包絡(luò)線，在任一點處的均值為0。

2 Prony和HHT分析在低頻振蕩辨識中的算例分析

2.1 Prony分析——4機11節(jié)點系統(tǒng)

為了檢驗廣域Prony分析方案的可行性，仿真、分析了IEEE 4機11節(jié)點系統(tǒng)。它是典型的2區(qū)域供電系統(tǒng)，存在1個區(qū)間震蕩模式（振蕩頻率0.64 Hz）和2個本地振蕩模式（振蕩頻率分別為1.12 Hz和1.16 Hz）[7]。4機11節(jié)點系統(tǒng)如圖1所示。

圖1 IEEE 4機11節(jié)點系統(tǒng)

MATLAB仿真平臺下，機組G1、G3處分別加入20 MVarr無功擾動，擾動持續(xù)0.5 s。分析機組G1、G3輸出的有功功率信號，如表1所示。

表1 不同模型階數(shù)的Prony分析結(jié)果—4機11節(jié)點系統(tǒng)

研究表明，當階數(shù)取5、7、9、11時，SNR值非常大且基本保持不變，Prony擬合準確；當階數(shù)取得過大時，會增加計算量，產(chǎn)生冗余。因此，階數(shù)取7最合適。階數(shù)為7時，分析結(jié)果如表1所示。1.12 Hz和0.64 Hz兩種低頻成分存在于發(fā)電機G1的有功信號中，1.15 Hz和0.64 Hz兩種低頻成分存在于發(fā)電機G3的有功信號中。這說明此系統(tǒng)的區(qū)間振蕩模式為0.64 Hz，發(fā)電機G1和發(fā)電機G3的本地振蕩模式分別是1.15 Hz和1.12 Hz，與系統(tǒng)自帶的分析結(jié)果基本一致。

圖2是階數(shù)為7時，Prony擬合算法對4機系統(tǒng)區(qū)域發(fā)電機G1發(fā)出的電磁功率的擬合。由圖2可知，此時Prony擬合非常準確。

圖2 Prony擬合曲線與原始曲線的比較—4機11節(jié)點系統(tǒng)

2.2 HHT分析—4機11節(jié)點系統(tǒng)

由以上Prony算法分析4機系統(tǒng)信號可知，4機系統(tǒng)含有3個振蕩模式，即2個本地模式和1個區(qū)間模式。由圖3可知，HHT算法對機端加20 MVar無功擾動，構(gòu)成小擾動情況下的發(fā)電機電磁功率辨識，并分解出3個IMF分量，而與原始曲線形狀最相似的是IMF1，可判定其為信號的主要成分。用Hilbert變換IMF1，得出瞬時幅值A(chǔ)1、瞬時頻率f1。由圖4可知，A1呈逐漸增大趨勢，與0.108的正衰減因子相對應(yīng)。在頻率圖上隨機標出一點，縱坐標軸為0.640 5 Hz，與原始值0.64 Hz相近，得出的阻尼比ζ也與原始值相近（見表2）。因此，可判定此分量是4機系統(tǒng)發(fā)生低頻振蕩時的區(qū)間振蕩模式。由于4機系統(tǒng)發(fā)生低頻振蕩時，1.16 Hz和1.12 Hz的兩個本地模式頻率太接近，EMD分解過程易發(fā)生模態(tài)混淆且無法將其準確分離，故分量IMF2、IMF3呈現(xiàn)無規(guī)則波動。不是單一的尺度，不符合IMF分量的條件。

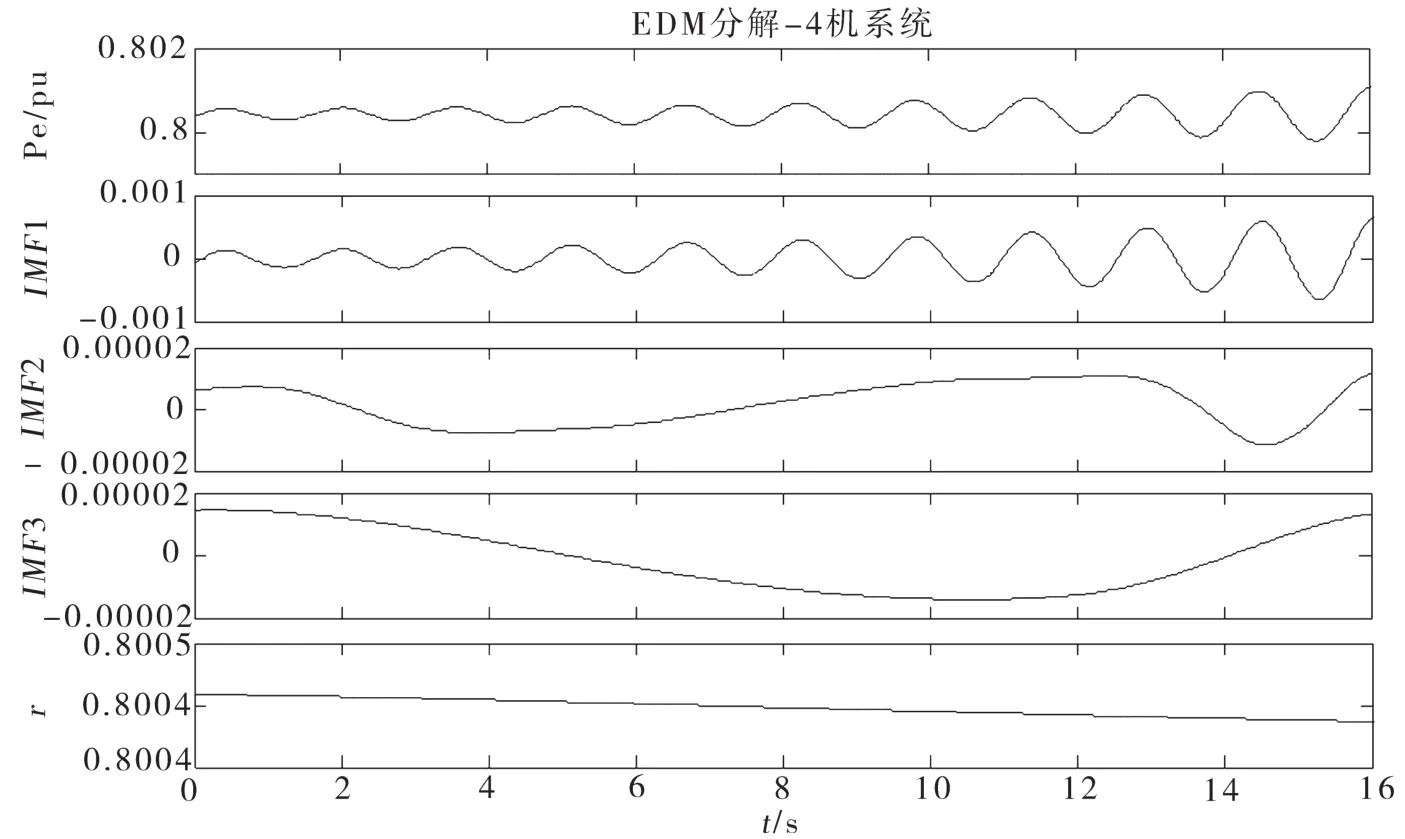
圖3 EMD分解結(jié)果—4機11節(jié)點系統(tǒng)

表2 Prony算法、HHT算法分析IMF1結(jié)果對比—4機11節(jié)點系統(tǒng)

圖4 分解出個各IMF分量的幅值、頻率

3 結(jié) 論

Prony算法和HHT算法是在線低頻分析、提取振蕩參數(shù)的有效方法。Prony算法是分析信號的時域，可以分析仿真結(jié)果，進行實時在線分析，辨識衰減較快的信號，但不能準確辨識系統(tǒng)的實際階數(shù)。HHT算法可以分析信號的時域和頻域，并進行線性化、平穩(wěn)化處理，但無法辨識衰減較快的信號，如4機系統(tǒng)仿真數(shù)據(jù)。綜上所述，兩種算法各有優(yōu)缺點，如果能克服端點效應(yīng)問題，HHT算法有望成為電力系統(tǒng)低頻振蕩在線分析的有力工具。