集裝箱正面吊運機位置分析

龍 順，康輝梅

（湖南師范大學工程與設計學院，湖南 長沙410081）

0 引言

集裝箱正面吊運機采用了汽車起重機的伸縮式臂架結構，利用伸縮臂擴展作業范圍，利用吊具裝卸、搬運貨物，具有起吊能力大、堆碼層數高、機動靈活、堆場利用率高等優點。主要應用于集裝箱港口、碼頭、鐵路和公路中轉站、堆場等集裝箱的裝卸、場地轉運及堆垛作業[1]。

近年來，對于集裝箱正面吊運機的研究主要集中在液壓系統及其控制方面[2-4]和結構強度方面[5-7]。為了準確、穩定對箱、堆垛，有必要對集裝箱正面吊運機的位置正解和反解進行分析。文獻[8]基于ADAMS仿真平臺對集裝箱正面吊運機進行了位置反解仿真分析。本文基于復數矢量法建立集裝箱正面吊運機的數學模型，求得解析解，進而利用Matlab軟件進行工程實例仿真分析，最后利用ADAMS軟件進行驗證。

1 數學模型的建立

集裝箱正面吊運機是一種空間開鏈機構，其機構示意圖如圖1所示，由二級伸縮式臂架系統和多功能吊具系統兩部分組成，采用液壓驅動方式。臂架系統包括基本臂和伸縮臂兩部分，基本臂在俯仰液壓油缸作用下繞O點轉動，實現臂架系統的俯仰運動；伸縮臂安裝在基本臂內，由臂架伸縮液壓油缸驅動，實現臂架系統的前后伸縮運動。多功能吊具系統由基本梁和伸縮梁組成，整體安裝在伸縮臂前端，基本梁在液壓馬達的作用下可繞伸縮臂在水平面內正反旋轉，本文假設基本梁無偏轉，即基本梁垂直于基本臂；伸縮梁在橫梁伸縮液壓油缸的驅動下可左右伸縮，調整吊具的開度。集裝箱正面吊運機通過臂架系統的俯仰運動、前后伸縮運動和吊具系統的旋轉運動的配合，實現對不同位置的集裝箱的作業；通過吊具系統的左右伸縮運動實現對不同規格的集裝箱的作業。

圖1 集裝箱正面吊運機機構示意圖

1.1 位置正解

集裝箱正面吊運機的位置正解是已知三個液壓油缸的長度（S1、S2、S3），求解吊具系統末端的坐標（xI、yI、zI）和（xH、yH、zH）。為了獲得吊具系統末端坐標的解析表達式，本文基于復數矢量法進行位置正解分析。

基本臂、俯仰液壓油缸和機架一起構成一個封閉矢量多邊形OABC，因此可建立矢量方程：

將式（1）表示為復數矢量形式為：

應用歐拉公式將上式實部和虛部分離、平方相加并整理化簡可得：

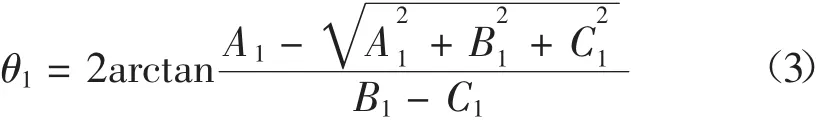
式中：

基本臂、伸縮臂和機架構成一個封閉矢量多邊形OADE，因此可得：

將式（4）表示為復數矢量形式為：

應用歐拉公式將式（5）右端的實部和虛部分離，可得：

綜合式（3）和式（6）可知 E 點的絕對坐標值（xE，0，zE）。

由基本梁和伸縮梁構成的封閉矢量三角形EGI可得：

將式（7）表示為復數矢量形式為：

由此可以求得I點相對E點的坐標：

聯立式（3）、（6）和（9）可求得 I點的絕對坐標值：

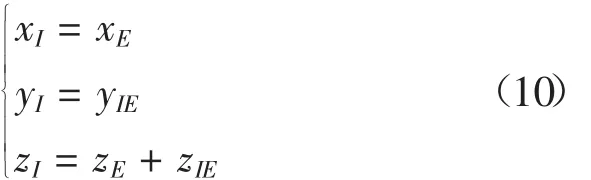
同理可得H點的絕對坐標值：

1.2 位置反解

集裝箱正面吊運機的位置反解是給定吊具系統末端的坐標（xI、yI、zI），求解三個驅動液壓油缸的長度（S1、S2、S3）。同理，本文基于復數矢量法進行位置反解的求解。

由基本梁和伸縮梁構成的封閉矢量三角形EGI創建封閉矢量方程：

將上述方程表示為復數矢量形式為：

根據式（13）和yE=0可求得：

進而求得E點的坐標如下：

由基本臂、伸縮臂和機架構成一個封閉矢量多邊形OADE，建立封閉矢量方程：

將式（16）表示為復數矢量形式為：

求解上式可得：

式中：A2=xEcosβ1-zEsinβ1

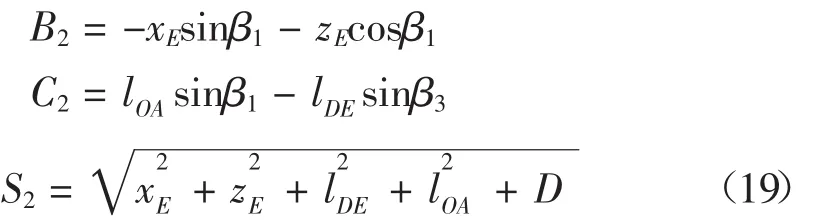
式中：

由基本臂、俯仰液壓油缸和機架一起構成的封閉矢量多邊形OABC，可建立封閉矢量方程：

將上述方程表示為復數矢量形式為：

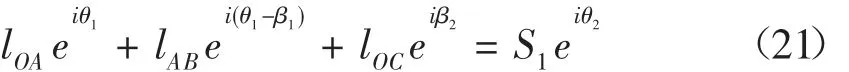
求解上式可得：

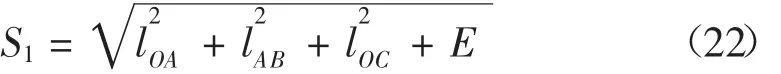
式中：

2 算例分析

以某集裝箱正面吊運機為研究對象，在Matlab中進行算例分析。主要參數設定為：lOA=215 mm，lAB=570mm，lOC=1001mm，lDE=617mm，lGI=468 mm，S1=878 mm，S2=2 645 mm，S3=1 124 mm，桿件之間的夾角設定如下：β1=90°，β2=140°，β3=80°.設定各液壓油缸的運動范圍如下：S1為878～1 198 mm；S2為2 600～3 496 mm；S3為1 124～1 444 mm.根據前文求得的位置正解的數學模型，在Matlab中編寫程序，得到集裝箱正面吊運機的工作空間如圖2所示。該工作空間展示的是以基本臂和機架的鉸點O為參考點的末端執行裝置I點的可運動范圍，I點在X軸方向的運動受S1和S2共同作用，其范圍為2 536～3 410 mm，且運動的過程為非線性遞增規律；在Y軸方向的運動受S3的作用，其范圍為1 124～1 444 mm，且運動的過程為線性遞增規律；在Z軸方向的運動受S1的作用，其范圍為-872～998 mm，且運動的過程為非線性遞增規律。

圖2 集裝箱正面吊運機的工作空間

在實際作業過程中，為防止集裝箱的振動、搖擺等不利因素，集裝箱正面吊運機應能勻速垂直起吊，即要求I點相對于O點而言X、Y方向不變，沿Z軸方向勻速運動。設定I點沿Z軸方向的移動速度為0.15 m/s，利用前文求得的位置反解數學模型在Matlab中編寫程序可以得到俯仰液壓油缸和伸縮液壓油缸的長度變化曲線分別如圖3和圖4所示。兩個液壓油缸的長度均不斷增長且均呈非線性變化規律，其中俯仰液壓油缸的變化相對比較緩慢，而臂架伸縮液壓油缸長度的變化越來越快。

圖3 俯仰液壓油缸的長度變化曲線

圖4 臂架伸縮液壓油缸的長度變化曲線

3 ADAMS驗證

在SOLIDWORKS中建立了集裝箱正面吊運機的三維模型后，將其保存為*.x_t格式后導入至ADAMS軟件，進而建立集裝箱正面吊運機的運動學仿真模型并對其進行運動仿真。

為驗證垂直起吊時俯仰液壓油缸和伸縮液壓油缸長度變化曲線的正確性，在ADAMS中進行仿真。在E點創建一個豎直向上的直線運動，滿足起吊速度為0.15 m/s的要求，得到俯仰液壓油缸和伸縮液壓油缸的長度S1和S2的變化曲線，如圖5所示。為了對比，將由本文所建數學模型而得的俯仰液壓油缸和伸縮液壓油缸的長度S1和S2的變化曲線也表示在圖5中。

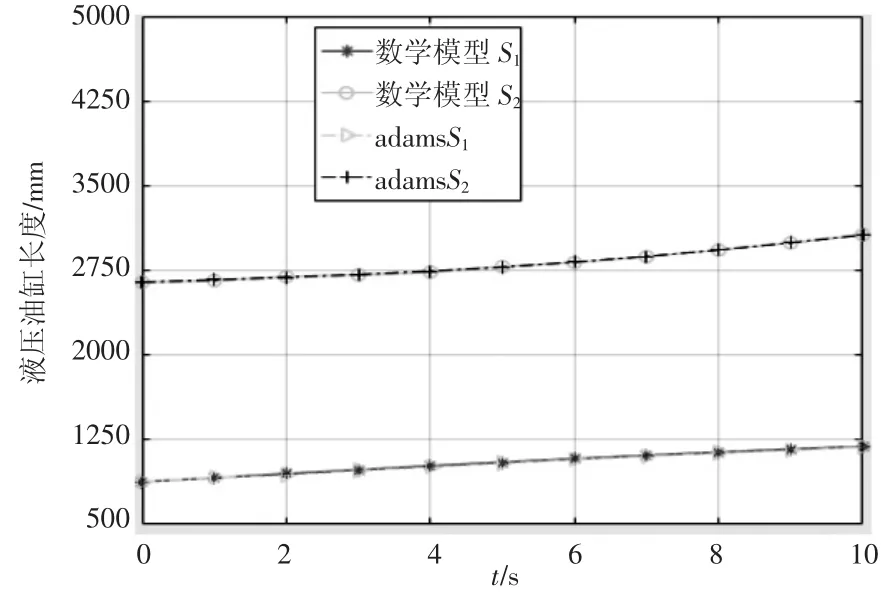
圖5 S1和S2長度變化對比曲線

對比圖5中的4條直線可知，ADAMS仿真得出的兩個液壓油缸的長度變化曲線與所建數學模型的長度變化曲線一致，驗證了所建數學模型的正確性。

4 結論

（1）基于復數矢量法，建立了集裝箱正面吊運機的數學模型，為位置分析提供了理論依據。

（2）基于數學模型對集裝箱正面吊運機進行了位置正反解的分析，并且利用Matlab仿真分析了該機構的工作空間和勻速垂直起吊時俯仰液壓油缸和伸縮液壓油缸的長度變化規律。

（3）位置分析結果對該機構的運動學分析和自動控制研究等具有重要參考價值。