曲面零件銑削加工表面粗糙度控制技術研究與應用

翟婷婷，韓曉光，付移風

（中國航發西安動力控制科技有限公司，陜西 西安710077）

近年來，隨著數控加工技術的發展和市場激烈的競爭，對產品加工質量和加工效率有著越來越高的要求。在滿足產品數控加工質量的前提下，提高加工效率是今后數控加工領域內研究的一個重要方向，而數控切削參數的合理選擇則是產品加工表面質量和加工效率的基本保障。在不同的表面粗糙度技術要求下，研究數控切削參數的優化組合將有著重要意義：它將能夠在未實際加工前就可較合理地選定加工參數，省去試切法的反復試驗，在大量減少試制工作的基礎上可以選擇效率最大的優化參數。然而曲面加工時的表面粗糙度形成機理還不成熟，尚未建立完整切削參數數據庫，同時工藝人員不得不依靠經驗進行選擇加工參數。為此有必要通過試驗建立精度和可靠性均提高的表面粗糙度數學模型，在實際加工前對表面粗糙度進行合理的預測，以確定合理的工藝切削解決方案。

目前，影響已加工表面粗糙度的因素可以分為兩種：幾何因素和物理因素。一般來說，物理因素包括：積削瘤、鯪刺、振動、切削刃的刃磨品質、工件材料組織的缺陷、切削液的使用情況等；幾何因素主要是切削刃與工件相對運動軌跡形成的表面粗糙度，通常與刀具和加工參數有關[1]。高速加工過程中，積削瘤與鯪刺幾乎不存在，因此刀具參數、切削用量等因素將成為影響被加工表面粗糙度的主要因素[2]。

目前，針對表面粗糙度預測模型的研究，已受到國內、外學者的廣泛關注。在國外，1976年，Tipnis等人提出了一個表面粗糙度實驗模型進行表面粗糙度的研究。1995年，Alauddin等人利用此模型進行多因素試驗研究分析，發現此預測模型與實驗數據之間有著良好的相互作用關系。在國內，也有學者對車削、銑削、磨削等不同加工方式的表面粗糙度進行了研究，但對高速精加工表面粗糙度的研究才剛剛起步。隨著對工件質量要求的提高和自動化加工的普及，應用表面粗糙度的預測將成為金屬切削加工質量分析的重要研究方向。但是關于表面粗糙度在高速銑削過程變化規律的詳細試驗數據分析研究尚少，針對高速切削工件已加工表面粗糙度形成機理還不完善，目前還沒有構建基于殘余高度的加工表面粗糙度預測模型。

為構建基于殘余高度的曲面零件銑削加工表面粗糙度預測模型，本文以曲面零件高速銑削加工為試驗對象，分析不同切削方式對殘余高度的影響，設計詳細試驗方案，構建表面粗糙度預測模型，分析主軸轉速、殘余高度等參數對表面粗糙的影響及原因，并通過加工試驗驗證表面粗糙度預測模型的有效性。

1 殘余高度計算

1.1 概述

在曲面零件的數控加工過程中，加工刀具通常采用球頭刀具、端銑刀以及環形刀具。球頭銑刀是三軸曲面加工比較常用的刀具，端銑刀是五軸曲面加工常用的刀具[3]。本文以球頭銑刀加工曲面零件為研究對象，存在兩種加工路徑：一種是刀具進給垂直曲面母線方向，如圖1所示；另一種是刀具進給平行曲面母線方向，如圖2所示。

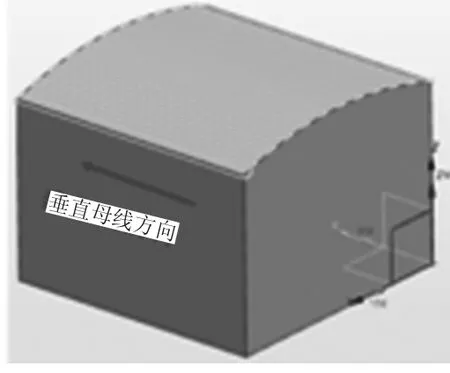
圖1 銑削方式1

圖2 銑削方式2

1.2 垂直曲面母線殘余高度

當刀具進給垂直曲面母線時，刀痕在切削行間形成了殘留高度Z與行距a和刀具半徑R以及曲面曲率半徑r密切相關，如圖3所示。

圖3 垂直曲面母線殘余高度參數關系示意圖

在此種刀具進給方式下，曲面切削殘留高度的計算公式如式（1）所示：

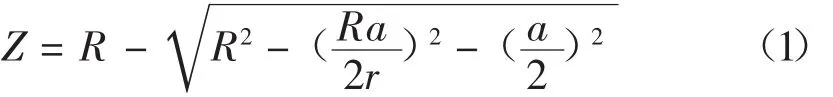
其中：Z為殘留高度；R為球頭刀半徑；a為行距；r為曲面曲率半徑。

1.3 平行曲面母線殘余高度

當刀具進給平行曲面母線時，刀痕在切削行間形成了殘留高度Z與刀具徑向切削深度a和刀具半徑R相關，如圖4所示。在此種刀具進給方式下，曲面殘留高度的計算公式如式（2）所示：

圖4 平行曲面母線殘余高度參數關系示意圖

其中：Z為殘留高度；R為球頭刀半徑；a為行距；由式（2）可知：當a=2R時，此時Z=R；當 a＞2R時，此時Z=ap.

對比式（1）和式（2）可知：在加工條件相同的情況下，垂直曲面母線進刀的殘余高度大于平行曲面母線進刀的殘余高度，所以為了降低表面殘余高度，優選的進刀方式為平行曲面母線方向進刀。

2 表面粗糙度計算

2.1 試驗設計

文獻[4]用徑向切寬ae構建了球形銑刀的粗糙度模型，雖然切削行距能間接體現加工殘留高度對表面粗糙度的影響，但是用切削行距構建的球刀粗糙度模型無法準確預測不同刀具直徑的切削情況，這類預測模型的通用性較差。鑒于上述分析，確定刀具進給速度v、主軸轉速n、軸向切深ap和加工殘余高度Z四個因素為球刀銑削粗糙度的主要因素。采用正交設計進行銑削試驗，每個因素各取4個水平，正交因素水平如表1所示。

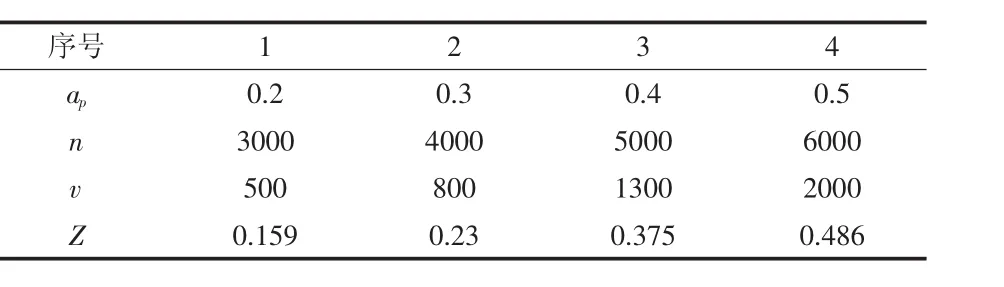
表1 試驗因素和水平選取表

2.2 切削試驗條件

加工設備：五軸高速加工中心（DMU60mono BLOCK）；加工刀具：圓柱直柄硬質合金球頭銑刀（直徑為Φ10；刃數為2）；加工材料為45#鋼，加工面為單一曲率曲面；冷卻方式為切削液冷卻。

2.3 試驗數據

依據文獻[5]的切削試驗，可以獲得表2所示的正交試驗數據。

表2 表面粗糙度正交試驗數據

（續下表）

（接上表）

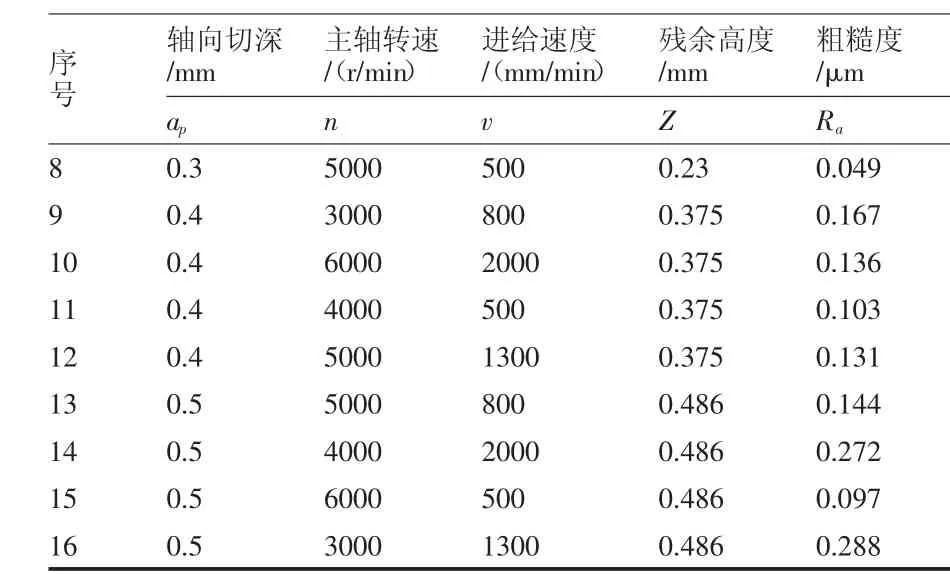
粗糙度/μm ap n v Z Ra 8 0.3 5000 500 0.23 0.049 9 0.4 3000 800 0.375 0.167 10 0.4 6000 2000 0.375 0.136 11 0.4 4000 500 0.375 0.103 12 0.4 5000 1300 0.375 0.131 13 0.5 5000 800 0.486 0.144 14 0.5 4000 2000 0.486 0.272 15 0.5 6000 500 0.486 0.097 16 0.5 3000 1300 0.486 0.288序號軸向切深/mm主軸轉速/（r/min）進給速度/（mm/min）殘余高度/mm

2.4 粗糙度數學模型建立

由于垂直曲面母線進刀的殘余高度大于平行曲面母線進刀的殘余高度，所以以平行曲面母線進刀方式進行計算，為了體現加工殘留高度對球頭銑刀切削表面粗糙度的影響，建立指數形式的數學模型，如式（3）所示：

該模型包含了五個參數，其中，k為切削條件綜合系數，ap為軸向切削深度，Z為加工殘留高度，n為主軸轉速，v 為刀具進給速度，c1、c2、c3、c4為指數系數。

為求得 c1、c2、c3、c4，對方程兩邊取對數，令y=lgRa、c0=lgk、x1=lgap、x2=lgZ、x3=lgn、x4=lgv.則指數方程轉化為線性方程，如式（4）所示：

利用表2中的正交試驗數據，對線性方程（5）進行多元線性回歸，即可求得回歸系數，即方程中的指數系數：c0=36.9、c1=0.511，c2=0.781、c3=-0.915、c4=0.473，因此球頭銑刀銑削粗糙度的數學模型為式（6）。

3 影響因素分析

3.1 主軸轉速

為求得表面粗糙度與主軸轉速單因素變量關系，設定 ap=0.2 mm、v=2 000 mm/min、Z=0.159 mm，此時主軸轉速與粗糙度的關系曲線如圖5所示。

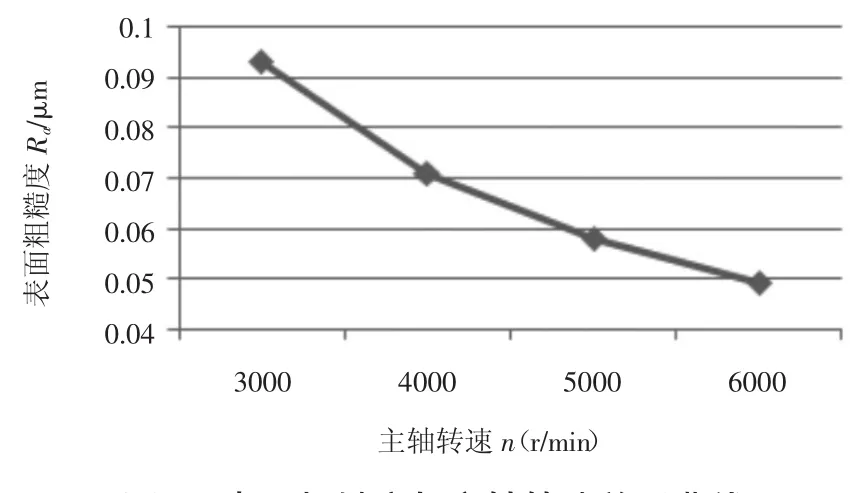
圖5 表面粗糙度與主軸轉速關系曲線

由圖5可知：表面粗糙度隨主軸轉速的增加而降低，但當主軸轉速升高到一定值之后，長時間的高速切削運動會使刀具磨損變得劇烈，表面粗糙度反而會增大。

3.2 進給速度

為求得表面粗糙度與進給速度的單因素變量關系，設定 n=5 000 r/min、ap=0.2 mm、Z=0.159 mm，此時表面粗糙度與進給速度的關系曲線如圖6所示，由圖可知：作為與進給速度交互作用對表面質量產生影響的一個參數，進給速度對表面粗糙度值的影響比較明顯。

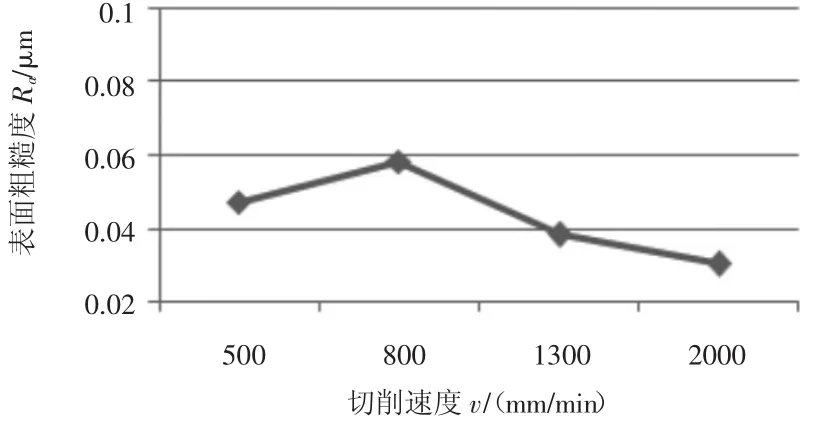
圖6 表面粗糙度與進給速度關系曲線

3.3 軸向切深

為求得表面粗糙度與軸向切深的單因素變量關系，設定 n=5 000 r/min、v=2 000 mm/min、Z=0.159 mm，此時表面粗糙度與軸向切深的關系曲線如圖7所示。

圖7 表面粗糙度與軸向切深關系曲線

由圖7可知：表面粗糙度值隨著切削深度的增大而變大，是因為隨著切削深度的增大，每齒切削量變大，會產生比較大的切削力，這種不斷變化的切削力使加工過程中產生較大震動，從而導致已加工表面質量的下降。

3.4 殘余高度

為求得表面粗糙度與切削深度單因素變量關系，設定 n=5 000 r/min、v=2 000 mm/min、ap=0.2 mm，此時表面粗糙度與殘余高度的關系曲線如圖8所示，由圖可知：表面粗糙度值隨著殘余高度的增大而變大，殘余高度對表面粗糙度的影響主要取決于所選刀具的直徑，在同一刀具直徑下，徑向進給量越小，球頭立銑刀的殘留高度相應越小，已加工表面粗糙度值也就可能隨之降低。

圖8 表面粗糙度與殘余高度關系曲線

4 試驗驗證

為驗證45#鋼球頭刀銑削的表面粗糙度數學模型的正確性，選擇試驗驗證條件如下：1）加工設備：DMU60monoBLOCK；2）加工刀具：硬質合金球頭銑刀（直徑 Φ10；刃數 2）；3）加工材料：45# 鋼，加工面為單一曲率曲面，曲率半徑150 mm；4）進刀方式：平行母線方向；5）檢測設備：Feica 3D白光干涉儀；6）試件：16件。試驗過程：按上述表2的加工參數對試件進行切削，對每件試件的粗糙度值分別進行3次檢測，將3次檢測結果的平均值作為試件粗糙度的實測結果，將表2的加工參數代入粗糙度數學模型，得到每組試驗件的粗糙度預測結果，對數學模型的預測誤差進行計算，計算公式為：預測誤差=，得到每組試驗件預測誤差，實測結果、預測結果及預測誤差數據見表3.

表3 實測結果、預測結果及預測誤差數據

由表3可知：數學模型預測誤差為3.06%～10.28%，表明該模型具有較高的預測精度，可以對加工零件的表面粗糙度進行預測。

5 結語

通過建立切削試驗及選定試驗參數，建立了45#鋼球頭刀銑削的表面粗糙度數學模型，通過驗證，數學模型的理論計算結果與實際計量結果相吻合，數學模型可以作為加工切削參數選擇和優化的理論依據；表面粗糙度數學模型的提出，為在保證加工精度的前提下提高切削效率提供了有效的解決途徑。