某中型履帶式挖掘機越障動力學建模與分析

秦仙蓉，趙書振，沈健花，張 氫，孫遠韜

（1.同濟大學 機械與能源工程學院，上海 201804；2.惠普信息技術研發有限公司,上海 200131）

由于工作性質的特點，履帶式挖掘機工作環境十分惡劣，經常需要跨越石塊、壕溝等障礙路面，而挖掘機的燃料箱等薄壁構件，在履帶式挖掘機越障過程中受到來自地面的振動沖擊，極易產生疲勞破壞，因此研究履帶式挖掘機的整機越障動力學特性十分必要。

近年來，國內外學者對履帶式挖掘機的研究主要有：履帶式挖掘機底盤系統的動力學分析，履帶式挖掘機的動力匹配及分析，履帶式挖掘機的工作裝置優化設計及可靠性分析等[1-5]。然而國內外針對履帶式挖掘機越障特性方面的研究還較為少見，有關越障特性的研究主要集中在履帶式移動機器人和高速履帶車輛（即履帶式裝甲車輛）。相應的研究主要集中于兩個方向：其一是研究對象為履帶式移動機器人，通過理論分析其越障時的性能和穩定性等特征，研究現有機構的優缺點并進行優化設計；其二是以履帶式裝甲車輛為研究對象，結合多剛體運動學和動力學分析，研究履帶式車輛在越障過程中的振動特性。

隨著計算機技術的飛速發展，虛擬樣機技術不斷進步，給履帶式車輛的研究提供了有效的研究手段。國內運用虛擬樣機技術進行挖掘機的仿真分析主要還是集中于工作裝置性能研究、最大挖掘機力、復雜作業工況的仿真以及機電液聯合仿真分析方面[6-8]，而關于履帶式挖掘機越障工況的仿真分析的文獻并不多見。

本文根據機械振動理論，以履帶式挖掘機為研究對象，建立挖掘機越障過程中的簡化力學模型和對應的數學模型，求解挖掘機越障過程中的動力學響應。建立某型履帶式挖掘機的整機虛擬樣機，實現多剛體動力學仿真，并與簡化力學模型數值求解結果進行對比。

1 簡化力學建模

考慮到履帶式挖掘機承載型底盤系統的特點，并借鑒國內外學者的研究，建立履帶式挖掘機的11自由度簡化力學模型，分別為車體的垂向位移、車體的俯仰角、與驅動輪接觸的履帶節單元垂向位移、7個與支重輪接觸的履帶節單元垂向位移和與導向輪接觸的履帶節單元垂向位移，如圖1所示。

圖1 履帶式挖掘機簡化力學模型

本力學模型不考慮履帶式挖掘機的側傾，即將問題簡化為二維問題。力學模型的坐標原點置于整機的質心位置，x軸的正方向為車體前進方向，z軸的正方向為垂直向上方向，符合右手坐標系原則。某中型履帶式挖掘機的單側履帶是由1個驅動輪、1個引導輪、7個支重輪、2個托鏈輪和1條履帶組成。考慮到整機在行走過程的托鏈輪對于地面緩沖能力明顯弱于其他輪子，且承載型底盤對地面緩沖作用主要是驅動輪、支重輪和引導輪通過履帶與地面接觸來實現，因此不考慮托鏈輪，除了車體的質量塊m10外分9個模塊，分別表示1個驅動輪、7個支重輪和1個引導輪與履帶板以及對應履帶板與地面之間的接觸作用。

圖1所示的力學模型中，m10表示車體質量；J表示車體轉動慣量；l1表示驅動輪到質心的距離；li(i=2，…，8)表示各支重輪到質心O的距離；l9表示引導輪到質心的距離；mi(i=1，…，9)表示與各輪接觸的履帶節單元的等效質量；k1、kb、k3分別表示驅動輪、支重輪與導向輪和履帶接觸的換算剛度，c1、cb、c3分別表示驅動輪、支重輪與導向輪和履帶接觸的換算阻尼，這里認為7個支重輪與履帶接觸的換算剛度（圖中都以kb表示）、換算阻尼相同（圖中都以cb表示）；k4、kd、k6和c4、cd、c6分別表示驅動輪、支重輪、導向輪下履帶節單元與地面接觸的換算剛度和換算阻尼，這里認為7個支重輪下履帶節單元與路面接觸的換算剛度（圖中都以kd表示）、換算阻尼（圖中都以cd表示）相同；ui(i=1，…，9)表示各輪下的路面激勵。

11自由度的廣義坐標為

其中：z表示車體的垂向位移，θ表示車體的俯仰角（逆時針為正），zi(i=1，…，)表示各等效質量的垂向位移。

建立簡化力學模型之后，由拉格朗日法可求得系統的運動微分方程為

其中，質量矩陣為

系統剛度矩陣為

系統阻尼矩陣為

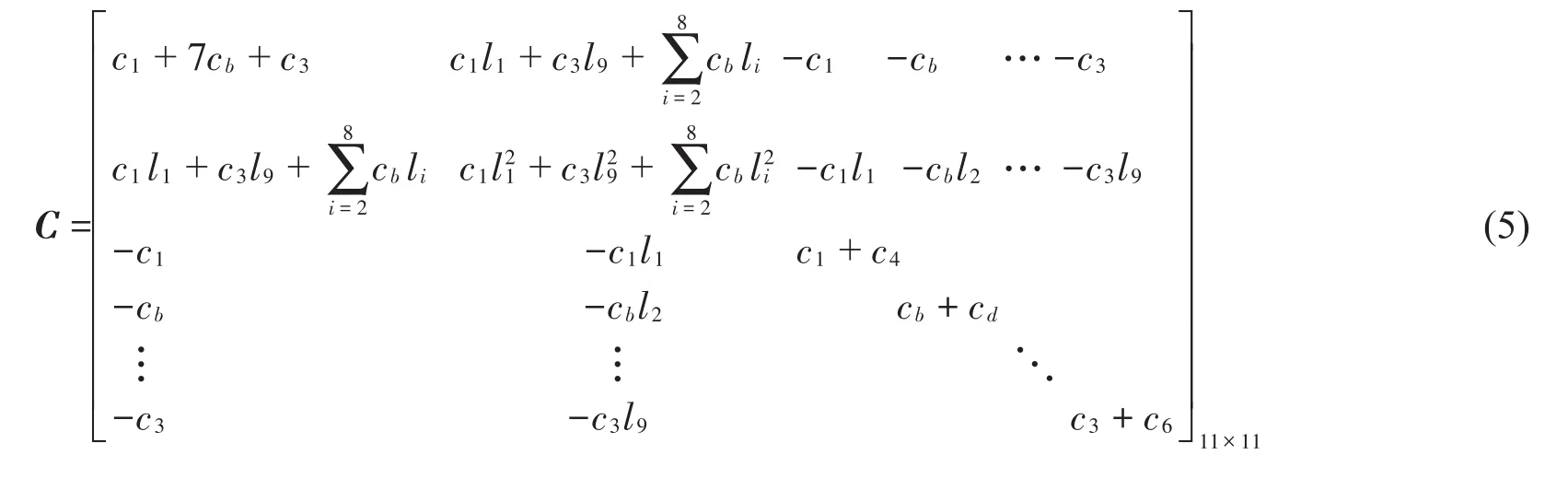
系統的廣義力矩陣為

綜上，建立了履帶式挖掘機的簡化力學模型以及相應的數學模型。

2 某中型履帶式挖掘機越障動力學分析

2.1 路面激勵參數確定

參考GB7031-1986《車輛振動輸入路面不平度表示方法》，本文采用的路面輸入形式有兩類：其一是垂直障礙物，其二是路面不平度。

2.1.1 路面障礙激勵

路面垂直障礙如圖2所示，障礙物的參數為高度h和長度l。對于某中型履帶式挖掘機，障礙物高度h設置為其極限越障高度h=0.267 m，設定長度l=0.5 m。

圖2 路面障礙激勵形式

由于履帶環將驅動輪、支重輪和引導輪圍成一個整體，當挖掘機某一輪子攀爬到障礙物邊緣時，其余各輪下的路面障礙參數h必大于等于0，因此該簡化力學模型的路面障礙激勵需要考慮履帶作用。主要分3個階段分析該型履帶式挖掘機越障過程中的路面障礙激勵：挖掘機爬上障礙物、在障礙物上行駛和駛下障礙物。

履帶式挖掘機的行駛速度分為兩檔：高速擋約0～1.53 m/s和低速擋約0～0.97 m/s，本模型研究的是履帶式挖掘機越障動態響應，行駛速度設為低速擋的最大值，約0.97 m/s。以自由度z5為例，在該自由度上，路面障礙激勵如圖3所示。

圖3 自由度z5的路面障礙激勵

2.1.2 路面不平度激勵

履帶式挖掘機在不平路面上行駛，使得各輪不斷受到路面障礙沖擊，產生較大的慣性力，進而造成挖掘機上薄弱環節的早期疲勞損壞，因此，在振動分析中考慮路面不平度的影響很有必要。大量的試驗測試表明：路面不平度是具有零均值、各態歷經的高斯隨機過程。國標GB7031-1986根據路面功率譜密度把路面不平度分為8級，據大量統計數據分析，履帶車輛經常作業的田野地面相當于F級路面，履帶車輛碾壓損壞的路面相當于G級，因此本文將模擬這兩種路面激勵。

根據國標中給出的路面不平度功率譜密度擬合公式，推導出路面不平度的理論計算公式，進而求出各輪的路面不平度激勵。

在后面的瞬態響應分析中，分兩種情況模擬路面激勵：

（1）如圖3所示，各自由度上只有路面障礙激勵；

（2）同時考慮兩種類型路面激勵，即將路面障礙激勵與路面不平度激勵疊加。仍以自由度z5為例，在該自由度上疊加后的路面激勵如圖4所示。

2.2 質量、剛度和阻尼參數確定

通過查找相關資料，結合三維實體模型，確定各部分的質量參數如表1所示。

學者Nakanishi.T和Shabana.A.A[9-10]對日本小松公司的PC120型履帶式挖掘機的各輪與履帶板以及履帶板與路面間的換算剛度和換算阻尼研究較為深入。考慮到履帶式挖掘機行走原理的相同性，本文中驅動輪、支重輪和引導輪與履帶板以及履帶板與地面之間的換算剛度和換算阻尼均參考文獻[10]中的換算剛度和阻尼，如表2所示。

圖4 自由度z5上路面障礙與不平度激勵疊加

表1 挖掘機力學模型質量參數

表2 力學模型中換算剛度和換算阻尼取值

為了后續模型響應的計算，還需確定各輪與質心之間的距離l1～l9。根據建立的三維實體模型確定這些尺寸參數的值{l1，l2,，… ，l9}={-2.087，-1.502，-1.017，-0.502，0.012，0.527，1.042，1.527，2.118}，單位為m。

2.3 動力學響應求解

根據所建立的動力學模型，運用狀態空間法建立系統的狀態方程，借助MATLAB，計算給定激勵下系統的動力學響應。

2.3.1 僅路面障礙激勵下的瞬態響應

僅考慮路面障礙參數作為激勵，求解得到車體質心垂向位移響應和垂向速度響應如圖5和圖6所示。

圖5 路面障礙激勵與車體質心垂向位移響應

如圖5所示，車體質心垂向位移響應與自由度z5上路面障礙激勵幾乎是吻合的，因為車體質心離z5的水平距離為0.012 m，幾乎在同一個垂線上。車體質心垂向位移響應可以看作是力學模型對一系列階躍激勵的響應，每一個階躍激勵表示車體的一個輪子爬上或爬下障礙物，共計9個階躍激勵。在2.5 s～3.5 s內車體垂向位移響應最大，最大值約0.31 m，均值約0.27 m，與預設的障礙高度0.267 m接近。

圖6為車體質心垂向速度響應，可以看出，車體每經歷一個路面輸入階躍激勵作用，車體的垂向速度會有較大幅度的波動，最大的速度幅值約為8m/s。結果符合理論分析和預期，能比較真實地反映實際履帶式挖掘機的越障動態響應，說明簡化力學模型較準確。

圖6 僅路面障礙激勵下車體質心垂向速度響應

2.3.2 路面障礙與路面不平度同時激勵下的瞬態響應

文中討論的路面不平度激勵級別為F級和G級，考慮路面障礙激勵和路面不平度兩種類型激勵的疊加，求解得到車體質心垂向位移響應和垂向速度響應如圖7。

如圖7所示，在G級路面不平度激勵下的車體質心垂向位移響應要大于在F級路面不平度激勵下的響應。

圖7 路面障礙與路面不平度同時激勵下的車體質心垂向位移響應

對比圖5和圖7可明顯發現，當路面障礙疊加路面不平度作為激勵時，車體質心垂向位移明顯增大，疊加F級路面不平度作激勵時，最大車體質心垂向位移響應約0.4 m；疊加G級路面不平度作激勵時，最大車體質心垂向位移響應約0.47 m

圖8 路面障礙與路面不平度同時激勵下的車體質心垂向速度響應

由圖8可得，在G級路面不平度激勵下，車體質心垂向速度響應幅值比F級路面不平度激勵下的響應要大，結果符合理論分析和預期。

3 履帶式挖掘機越障動力學仿真

通過建立前文所述履帶式挖掘機的虛擬樣機模型，進行越障動力學仿真，將動力學仿真結果與前文所得數值分析結果對比，對兩個模型進行相互校驗。

采用三維建模軟件建立履帶式挖掘機的實體模型，將其導入ADAMS。為減小計算量，對模型做相應簡化：只建立單側履帶；將工作裝置省去并根據其重力在履帶的行走架上添加相應的力；忽略一些次要零件比如銷套、螺栓螺母等。添加約束，定義各零件之間的運動關系：驅動輪、7個支重輪、導向輪與2個托鏈輪和行車架用旋轉副連接；55個履帶節單元之間用旋轉副連接；車體和行車架之間添加固定副。添加驅動：以轉動角速度的形式施加到驅動輪上，使模型能達到與前面相同的前進運動狀態。建立的虛擬樣機模型如圖9所示。

圖9 ADAMS虛擬樣機模型

ADAMS中接觸有兩大類：瞬時接觸和連續接觸。瞬時接觸使用的是彈簧阻尼模型，而連續接觸采用的是非線性彈簧模型。本研究課題中履帶節單元與各輪子和地面之間的接觸屬于瞬時接觸，因為在每一時刻只有特定數量的履帶節單元與各輪子和地面接觸。所有零件之間的接觸均采用impact接觸力來實現，采用ADAMS自帶的宏命令Macros功能，編寫cmd程序，實現近700對接觸力的自動添加。

在ADAMS中進行參數設置，如表3所示。剛度是接觸的剛度；作用因子是計算瞬時法向力時剛度的貢獻值指數，對于金屬通常取1.3～1.5；阻尼是指接觸的阻尼屬性，一般取為剛度值的0.1%～1%。選定接觸摩擦力為庫倫摩擦形式時，還需要定義靜摩擦系數、動摩擦系數、引起摩擦系數變化的速度臨界值黏滯轉換速度（由動摩擦轉變為靜摩擦）和摩擦轉換速度（由靜摩擦轉變為動摩擦）等參數。

動力學仿真初始條件設置與簡化力學模型計算條件相同，即驅動輪恒定轉速為125 deg/s（2.18 rad/s），使樣機前進速度達到0.97 m/s。外部激勵選為相同的路面垂直障礙物激勵，障礙物高度為0.267 m，寬度為0.5 m，仿真總時長為6.5 s，仿真步數為2 000步。

將ADAMS虛擬樣機仿真所得的車體質心垂向位移響應與簡化力學建模所得的結果對比，結果如圖10所示。

由圖10可知，在初始條件設置相同時，虛擬樣機仿真所得結果與簡化力學建模所得結果趨勢一致，簡化力學建模所得的車體質心垂向位移響應最大值約為0.31 m，在6 s之后車體質心垂向位移響應趨于平穩；虛擬樣機仿真所得的車體質心垂向位移響應最大值約為0.28 m，約6.1 s后曲線趨于平穩，越障過程結束。以車體質心垂向位移響應為例，說明了兩種動力學建模及分析方法具有可比性，可以相互校驗。

雖然兩種分析方法所得的結果趨勢一致，但在響應速度上有一定差異，主要原因是模型建立方法的差別和參數設置的不同。簡化力學模型剛性更強。

表3 虛擬樣機模型接觸參數設置

圖10 兩種模型車體質心垂向位移響應對比

4 結語

以某中型履帶式挖掘機為工程實例，建立了履帶式挖掘機越障過程的簡化力學模型和對應的數學模型，求解了其越障過程的動力學響應。同時，建立該履帶式挖掘機的整機虛擬樣機，實現多剛體動力學仿真。

在只有路面越障參數激勵下，根據所建立的簡化力學模型求得的車體質心垂向位移響應的均值約0.27 m，與預設的障礙高度0.267 m接近，符合理論分析和結果預測。

考慮路面不平度與路面障礙共同激勵時，簡化力學模型在G級路面不平度和路面共同激勵、F級路面不平度和路面垂直障礙共同激勵兩種情況下，車體質心垂向位移及速度響應幅值符合理論分析和預期，說明所建模型可以達到挖掘機非作業狀態動態特性研究的要求。

在只有路面垂直障礙物激勵時，以虛擬樣機模型為系統，通過仿真，將得到的結果與簡化力學模型的結果對比，發現車體垂向位移響應趨勢基本一致，實現了兩種動力學模型的相互校驗，說明了所提出的動力學建模與分析方法的正確性，可為履帶式挖掘機越障動態特性研究提供借鑒與參考。