不同車載工況下橋梁振動響應(yīng)試驗

梁 麗，李順才，2

（1.江蘇師范大學(xué) 機電工程學(xué)院，江蘇 徐州 221116；2.江蘇師范大學(xué) 江蘇圣理工學(xué)院，江蘇 徐州 221116）

車輛通過橋梁時，車載及其移動效應(yīng)會引起橋梁結(jié)構(gòu)振動，而橋梁的振動反過來又會影響車輛的正常行駛。橋梁在車輛通過時除了要承受靜力作用，還要承受由于振動而產(chǎn)生的慣性力。這些力的長期作用，會導(dǎo)致橋梁結(jié)構(gòu)產(chǎn)生疲勞，降低橋梁的結(jié)構(gòu)穩(wěn)定性、縮短橋梁使用壽命。當(dāng)移動車輛對橋梁的激振頻率接近于橋梁的某階固有頻率時，會產(chǎn)生共振現(xiàn)象，橋梁振動加劇，將直接威脅人們的生命安全，因而移動載荷作用下橋梁的振動響應(yīng)一直是交通安全研究的一個重要課題。

橋梁振動問題的研究始于鐵路橋梁，人類自1825年建成第一條鐵路以來，便開始探索、研究列車-橋梁的相互作用。爾后，隨著公路橋梁的廣泛應(yīng)用，人們提出了許多求解車載作用下橋梁動力響應(yīng)的簡便計算方法。Law和Zhu用能量法推導(dǎo)出車-橋耦合方程，分析了橋面不平整度和車輛制動因素對多跨梁振動響應(yīng)的影響[1]；Yang[2]等采用模態(tài)級數(shù)展開法分析了自由和強迫振動下含裂紋梁的響應(yīng)；Zhong[3]等建立了考慮預(yù)應(yīng)力效應(yīng)的橋梁-車輛模型證實了預(yù)應(yīng)力對車輛的最大垂直加速度有顯著影響；An[4]等人依據(jù)彈性系統(tǒng)的總勢能平衡原理和定位原則建立了車-橋耦合系統(tǒng)的動力響應(yīng)方程，研究了大跨度連續(xù)梁橋在車載作用下的動力響應(yīng)；王解軍[5]提出了移動車輛荷載作用下大跨橋梁隨機振動的計算模式；葉茂[6]等人建立了多個移動車輛系統(tǒng)-橋的耦合力學(xué)分析模型，給出了整個車-橋耦合系統(tǒng)演變隨機響應(yīng)的求解方法；袁宏智[7]等人將漂浮體系的斜拉橋結(jié)構(gòu)簡化成兩端簡支且中間離散彈性支撐梁、變地基系數(shù)梁和均勻地基系數(shù)地基梁3種模型，并建立了移動載荷作用下斜拉橋結(jié)構(gòu)的動力學(xué)方程；程帥奇[8]等討論移動簡諧力作用下變截面橋梁的振動，為研究車載對橋的作用提供了一種簡便方法。

隨著計算機科學(xué)技術(shù)的發(fā)展，有限元模擬成為研究車-橋耦合系統(tǒng)動力響應(yīng)的主要手段。Lu等人[9]應(yīng)用有限元法將含裂紋橋梁結(jié)構(gòu)離散為兩跨弱耦合Euler-Bernoulli梁模型，研究了該系統(tǒng)由于局部損傷而引起的振動模態(tài)局部化現(xiàn)象；趙俊[10]等運用Ansys軟件建立了裂紋梁模型，對移動載荷進行了瞬態(tài)分析；Li[11]等用直接剛度法建立了一種由三維車輛模型組成的耦合列車-橋系統(tǒng)模型，采用彈性有限元法計算橋梁動應(yīng)力響應(yīng)，并通過試驗驗證了該方法的準(zhǔn)確性；Zeng[12]等人利用有限元模型和多體系統(tǒng)對高速行駛的車載作用下的橋梁的動力響應(yīng)進行了研究；Li[13]等通過建立精細的三維有限元模型來表征橋梁的復(fù)雜結(jié)構(gòu)力學(xué)性能，并建立了車輛-橋耦合振動(VBCV)模型和16自由度車輛模型，以模擬車輛行駛時的動態(tài)行為；張亞賓[14]等人利用ANSYS軟件模擬計算了車輛以不同速度通過橋梁時，橋體的動態(tài)響應(yīng)；陳強[15]等人采用有限元法和振型疊加法相結(jié)合的建模方法，分析了支撐梁在具有大速度、加速度或大質(zhì)量的移動載荷作用下動力響應(yīng)問題；范琪[16]等人采用有限元法對勻速移動常量力和勻速移動簡諧力作用下簡支梁橋的動態(tài)響應(yīng)進行了研究。

現(xiàn)有文獻對橋梁振動響應(yīng)的研究大多集中在理論分析和數(shù)值模擬兩方面，而大部分文獻中給出的用于求解橋梁振動響應(yīng)的理論計算方法又較為繁瑣，且給出的結(jié)果一般為數(shù)值解，無法獲得精確的解析解。另外，現(xiàn)有文獻多通過構(gòu)建車-橋模型，通過數(shù)值模擬軟件模擬分析橋梁振動，或通過搭建室內(nèi)試驗臺進行測試，但這2種方法存在2個缺點，其一，現(xiàn)有數(shù)值模擬軟件應(yīng)用較為廣泛的為ANSYS，但要熟練操作該軟件前期需花費大量精力和時間進行學(xué)習(xí)，而室內(nèi)試驗臺即便按原型按比例進行縮小復(fù)制，試驗過程中仍與實地測試有所差別，導(dǎo)致最終數(shù)據(jù)存在誤差。且搭建試驗臺需充足資金和空間，條件限制過大，因而整體上現(xiàn)有文獻中關(guān)于橋梁振動的實測成果相對較少。現(xiàn)場實測受設(shè)備、環(huán)境、車載狀態(tài)等多種因素影響，還需實行交通管制，因而較難實現(xiàn)。本文主要通過試驗研究3種車載工況下橋梁的振動響應(yīng)，探索車載工況、車載速度及車載運行方向?qū)蛄赫駝禹憫?yīng)的影響。

1 移動車載作用下單跨簡支梁振動響應(yīng)的理論研究

不失一般性，本文以單跨簡支梁為理論分析模型，如圖1所示。

圖1 單車載作用下單跨簡支梁力學(xué)模型

橋梁上分別作用有以速度vA和vB勻速正向及反向行駛的車載A、B，P0和P1分別為A車分配到前端車輪和后端車輪的重量，P2和P3分別為B車分配到前端車輪和后端車輪的重量；dA、dB為A、B 2車前后輪之間的距離；R0和R1分別為2個支座的約束反力；設(shè)t=0時，橋梁靜止且車載A、B分別位于橋梁的最左端和最右端。當(dāng)移動載荷A、B分別向右端和向左端行駛時，對圖1梁的響應(yīng)進行求解。

為建立移動載荷作用下單跨簡支梁的振動響應(yīng)方程，首先引入奇異函數(shù)[17]

式中：括號<＞一般稱為麥考利括號。

當(dāng)n≥0時，

當(dāng)n<0時

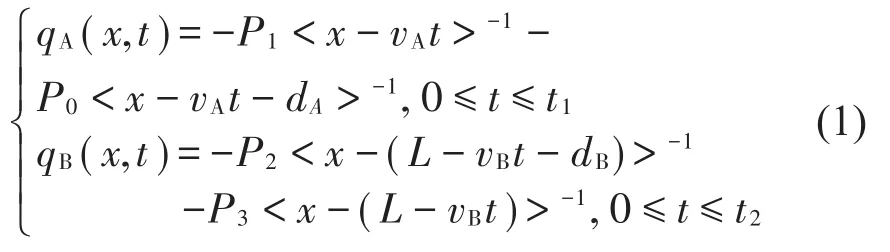
梁的橫向強迫振動方程為

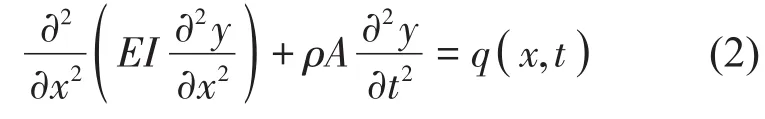
其中：EI為梁的抗彎剛度，ρ為該梁的單位體積質(zhì)量，A為該梁的橫截面積。

設(shè)單跨簡支梁橫向強迫振動解為

其中：ηi(t)稱為正則坐標(biāo)，Yi(x)為經(jīng)過歸一化處理的正則振型[18]

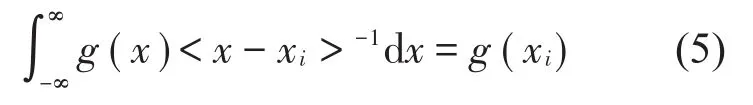
可分別計算出正則廣義力為

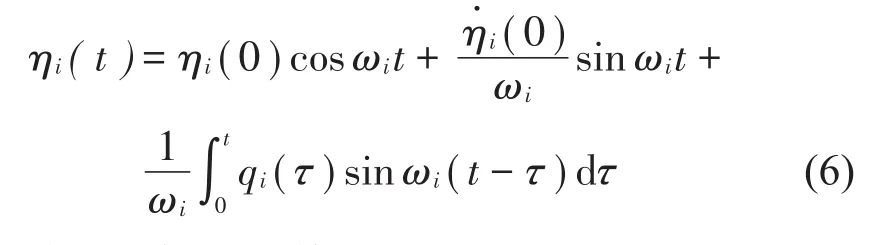
初始時刻橋梁是靜止的，ηi(0)=0,η˙i(0)=0[18]，則正則坐標(biāo)響應(yīng)為

將求出的正則響應(yīng)代入方程式(3)，即可得到車載通過時橋梁的振動響應(yīng)。

由上述推導(dǎo)可知，車載速度、行駛方向及車載重量影響橋梁各截面的振動響應(yīng)。彈性范圍內(nèi)梁的振動響應(yīng)與車載重量成正比，同向多車載作用下的響應(yīng)可通過單車載作用下的響應(yīng)進行疊加得到。下面以雙車同向或相向行駛時的橋梁為例，對比分析不同車載工況、不同車載速度下單跨簡支梁的振動響應(yīng)。

假設(shè)單跨簡支梁上同時作用有同向行駛或相向行駛的2個車載。為便于比較分析其他因素對試驗結(jié)果的影響，選取A、B 2車的車型完全相同，車載為別克，車重 1 220 kg，則P0=P2=7 320 N，P1=P3=4 880 N，前后車輪間距dA=dB=2.64 m。給定車載的移動速度為vA=vB=10、20、30、40 km/h。橋長L=60 m，單位體積質(zhì)量ρ=3 125 kg/m3，抗彎剛度EI=0.532 TN·m2；橫截面積A=14 m2。運用Mathcad分別求解車載正向及反向行駛時的振動響應(yīng)。由式（3）得到位移，求導(dǎo)后得到加速度響應(yīng)。表1給出了最大振動加速度amax及其所在截面xm。

表1 雙車載作用下橋梁的最大加速度及其所在截面xm

根據(jù)表1可知：

（1）在不考慮阻尼及其他因素影響的理想模型中，車速對橋梁的振動加速度影響不大；

（2）雙車同向行駛時，沿長度方向，橋梁的最大振動加速度位置位于離出發(fā)點橋梁的四分之一處。之后沿著車載移動方向，各截面加速度振幅呈衰減趨勢；

（3）同重量的雙車載相向行駛時，橋梁的振動加速度沿長度方向近似按正弦規(guī)律分布。

2 不同車載工況下橋梁振動響應(yīng)的試驗研究

2.1 測試設(shè)備及測試原理

以江蘇師范大學(xué)校內(nèi)玉泉橋為測試對象，測試設(shè)備為江蘇泰斯特集團生產(chǎn)的TST5925EV無線遙測動態(tài)應(yīng)變測試分析系統(tǒng)，如圖2所示。該測試系統(tǒng)主要由測試分析軟件、多個TST5925EV無線遙測動態(tài)應(yīng)變采集模塊、TST126傳感器、天線、無線路由器，移動電源及筆記本電腦等組成。該系統(tǒng)采用Wi-Fi無線傳輸技術(shù)，可靠傳輸距離約200 m，每臺計算機可同時控制16個采集模塊；該采集模塊采用嵌入式GPS模塊，實現(xiàn)多臺同步采樣。

圖2 TST5925EV無線遙測動態(tài)應(yīng)變測試分析系統(tǒng)

2.2 試驗方案及測試步驟

2.2.1 測點布置

玉泉橋橋長約為60 m、寬度為7 m，雙向單車道，有大約3度左右的坡度，該橋為4孔拱橋，下層為花崗巖，上層為平鋪型混凝土板梁（如圖3所示）。

圖3 玉泉橋

在玉泉橋橋面兩側(cè)各均勻設(shè)置4個測試點，共8個測點（如圖4、圖5所示）；相鄰2個測點之間距離為2 m，將8個TST126傳感器分別放置在各個測點處，底端用橡皮泥與地面固定以保持水平。

圖4 測點分布示意圖

圖5 現(xiàn)場測點分布

將TST126傳感器調(diào)至0檔（加速度檔），橋面左右兩側(cè)各放置一個TST5925EV采集模塊，每個采集模塊連接4個TST126傳感器，對應(yīng)軟件采集通道、傳感器編號及傳感器靈敏度如表2所示。

2.2.2 測試方案

測定車載速度、車載數(shù)量及車載運行方向?qū)蛄赫駝禹憫?yīng)的影響，設(shè)計3種試驗方案：

方案一（單車載）：單一車載以給定速度10 km/h、20 km/h、30 km/h、40 km/h由西向東在橋上駛過，通過TST126傳感器記錄各個測點的加速度響應(yīng)；

方案二（同向雙車載）：兩車同時以給定速度10 km/h、20 km/h、30 km/h、40 km/h由西向東同向駛過橋梁；

方案三（相向雙車載）：2車同時以給定速度10 km/h、20 km/h、30 km/h、40 km/h，向駛過橋梁，即一車由東向西，另一車同時由西向東行駛；

2.2.3 試驗步驟

(1)8臺TST126傳感器分別對應(yīng)接入1號和3號TST5925EV采集模塊；

(2)兩臺TST5925EV采集模塊分別接入發(fā)射天線，無線路由器插孔內(nèi)接入網(wǎng)線及接收天線，網(wǎng)線另一端接入筆記本電腦；

(3)在認真檢查所有接口是否接觸良好，檢查所有裝置是否安全可靠后，接通并打開儀器的電源；

(4)在配套的TST5925EV無線遙測動態(tài)應(yīng)變測試分析軟件上設(shè)置加速度工程單位為mm/s2，采樣頻率為200 Hz，分析頻率為78.13 Hz，采樣模式為連續(xù)采集，觸發(fā)方式為自由觸發(fā)，測量類型為電壓測量，并根據(jù)傳感器編號設(shè)置對應(yīng)通道靈敏度（如表3所示），窗類型為矩形窗，每次采樣時間5分鐘。

(5)采集前，進行平衡與清零，隨后在車載啟動時點擊開始采集，車載駛下橋梁時點擊停止采集。

3 試驗結(jié)果及分析

3.1 單一車載作用下橋梁各截面的加速度響應(yīng)

根據(jù)試驗測試結(jié)果，單車載以10 km/h的速度由西向東駛過橋梁時，截面A處的加速度時域曲線如圖6所示。

由該曲線可得1號和5號傳感器所測得的amax分別為3.53 mm/s2及2.82 mm/s2，由于1號及5號傳感器位于同一截面，為便于分析，對同一截面兩個傳感器數(shù)據(jù)取平均得該截面處的amax為3.175 mm/s2。由于汽車由西向東駛過截面，故設(shè)定西側(cè)為起始位置，則各截面所處的具體位置及單一車載以20 km/h、30 km/h、40 km/h的速度駛過橋梁時各截面處的加速度最大值amax如表3所示。

表2 采集通道、傳感器編號及傳感器靈敏度V/(mm?s-1)

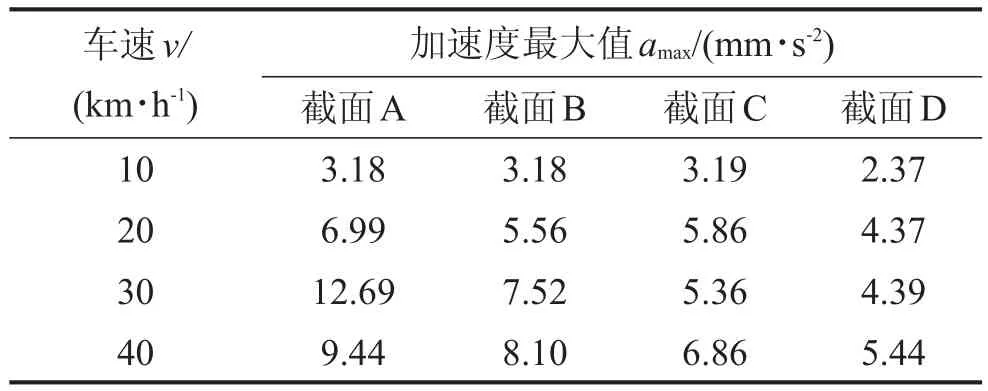
表3 單一車載行駛時各截面處的amax

根據(jù)表3可知：

（1）隨車速增大，各截面amax總體呈遞增趨勢；

（2）車速較低時，各截面的amax相差不大，當(dāng)車速為30 km/h時，amax值最大；

（3）相同車速下，由于截面A處在跨中無橋墩位置處，故截面A處的amax最大。

3.2 雙車同向及相向行駛時橋梁各截面加速度響應(yīng)

同理可得到雙車載以不同速度同向及相向駛過橋梁時各截面處的amax如表4所示。

由表4可知：

（1）車速較低時，各截面amax相差很小；

（2）相同車速時，截面A處的amax最大；

（3）雙車載同向行駛時，截面A、B的amax隨車速的增大而增大；雙車載相向行駛時，截面B、C處的amax隨車速的增大而增大；

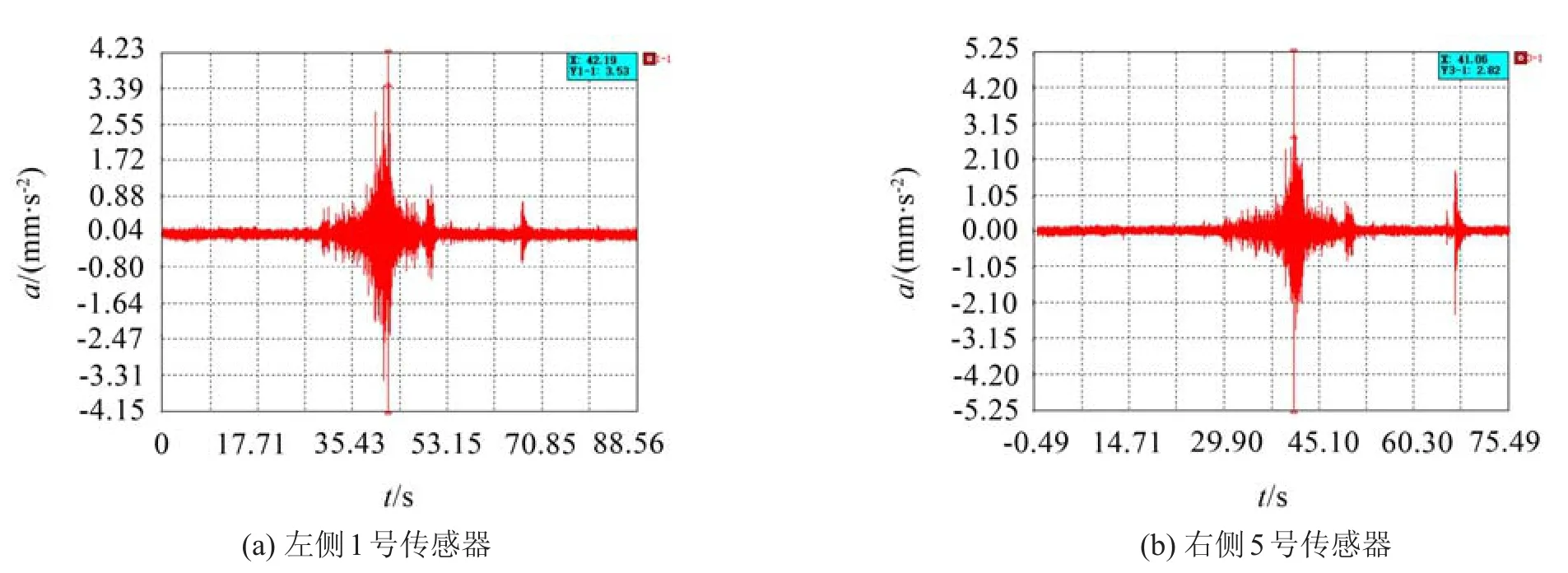
圖6 單車載作用下截面A處兩側(cè)的加速度時域曲線

（4）雙車同向行駛時，截面C、D處的amax隨車速的增大呈先增后減趨勢；而雙車相向行駛時，截面A、D處的amax隨車速的增大呈先增后減趨勢，主要原因在于橋東西兩側(cè)剛上橋面處各存在一減速帶，人為駕駛車輛在車速較大靠近減速帶時下意識進行了減速，導(dǎo)致結(jié)果出現(xiàn)誤差。

表4 雙車載同向及相向行駛時各截面處的amax

（5）根據(jù)理論分析，同向雙車載作用下橋梁的amax應(yīng)為單車載作用下的兩倍，但根據(jù)實測數(shù)據(jù)，同向雙車載作用下橋梁的amax較之單車載作用下amax的兩倍要小，主要是因為實測時橋梁的阻尼對振動有影響，理論分析沒考慮阻尼作用。此外測點分布不嚴格對稱，且車載行駛由人為控制，有誤差。

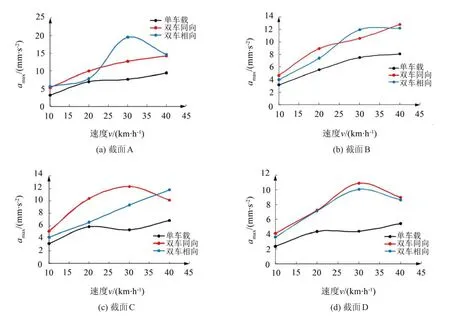
圖7 不同工況下各截面最大加速度隨車速的變化曲線

3.3 同一截面不同工況下的加速度峰值比較

由表3、表4可繪制出不同車載工況下各截面最大加速度amax隨車速的變化曲線，如圖7所示。

由圖可知：

（1）單車載作用下，橋梁的amax最小，與理論計算一致；

（2）對于截面A、B，雙車相向行駛時的amax最大，而對于C、D截面雙車同向行駛時的amax最大。

（3）各截面在車速為30 km/h時的amax最大；

（4）截面B與截面C處的amax相近，由理論分析可知，對稱截面處的amax應(yīng)相同，但截面A與截面D處最大加速度值相差較大，結(jié)合試驗現(xiàn)場可知，由于截面D處設(shè)置的測點位于橋墩處導(dǎo)致最大加速度值較小；

（5）綜合圖7中4圖可知，由于截面A處于跨中無橋墩處，故截面A處的amax最大。

4 結(jié)語

本文通過理論及無線動態(tài)振動測試技術(shù)研究了橋梁在不同車載工況及不同車載速度下的振動響應(yīng)，得到了各截面加速度峰值隨車載速度的變化曲線、各車載速度工況下不同截面加速度峰值的變化規(guī)律，主要結(jié)論如下：

（1）根據(jù)實測，不同車載工況作用下，由于截面A處于跨中無橋墩處，該截面處的amax最大；車速較低時，各截面amax相差很小；總體上來說，當(dāng)車速為30 km/h時，各截面的amax最大；

（2）根據(jù)實測，同向雙車載作用下橋梁的amax較之單車載作用下amax的兩倍較小，與理論分析結(jié)果不一致，主要是由于現(xiàn)場實測時，所選用的兩車載型號并非完全一致，理論分析時沒有考慮橋梁的阻尼作用，人為控制車載行駛速度，導(dǎo)致誤差產(chǎn)生；

（3）對于橋東A、B兩個截面，車速較小時，雙車同向比雙車相向時梁的加速度峰值高；而在車速較大時，情況則相反；對于橋西C、D兩個截面，雙車同向均比雙車相向時的加速度峰值高；

（4）由于測試時總的車速不高，無線動態(tài)設(shè)備采集頻率范圍有限，故本文未做頻域分析，以后可以選取較大的多跨橋梁進一步進行試驗研究并進行相應(yīng)的時域、頻域分析。