并聯雙向偏轉工作臺的動力學仿真與分析

陳 周 陳 純

（陜西理工大學 機械工程學院，漢中 723000）

并聯機構結構的高復雜性，導致其動力學模型系統具備非線性、多自由度和多參數耦合的特點，是研究并聯機構動力學的一個重點和難點。本文對一種并聯雙向偏轉工作臺并聯機構進行了分析，并基于Lagrange法對該并聯機構進行了動力學方程的建立，同時利用admas軟件對該機構進行了動力學仿真，為該機構實際應用與分析提供了力學研究支持。

1 雙向偏轉工作臺并聯機構簡介

該雙向偏轉工作臺內、外齒輪拱，各由一個獨立固定在底座上的電機進行驅動，外齒輪拱通過銷軸直接連接在臺面下的銷軸座上，但如果內、外齒輪拱均用普通的銷軸與工作臺連接，則無法實現兩個方向齒輪同時轉動且互不干擾的。假如X方向（外齒輪拱轉動方向）上發生45°轉動時，Y方向（內齒輪拱轉動方向）上的轉動軸就從原來的水平角度轉軸變成了現在的45°轉軸，如果要圍繞此軸轉動，Y方向的轉動方向必須與此45°轉軸垂直，然而此時Y方向的轉動軸仍然是原來的水平方向的轉動軸，兩者發生沖突。因此為了能滿足內外齒輪同時轉動功能，現對內齒輪拱與工作臺臺面的連接方式進行優化，采用U形孔及銷軸的搭配設計，該優化原理類似于萬向節轉動原理，保持兩個方向上的轉軸始終垂直。此并聯雙向偏轉工作臺運動學逆解如式（1）、式（2）所示。

正解如式（3）、式（4）所示

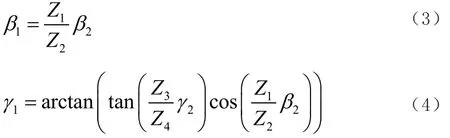
式中，Z1為驅動外齒輪拱電機上的消隙齒輪齒數；Z2為外齒輪拱齒數；Z3為驅動內齒輪拱電機上的消隙齒輪齒數；Z4為內齒輪拱齒數；β1為基于電機轉動角度的外齒輪拱偏轉角度；β2為驅動外齒輪拱電機轉動角度；γ1為基于電機轉動角度的內齒輪拱偏轉角度；γ2為驅動內齒輪拱電機轉動角度。

2 廣義力

由于該機構含有兩個轉動自由度，因此用沿內、外齒輪拱轉動方向轉動的廣義坐標qk（k=1,2）來描述該工作臺的運動.為求在廣義坐標qk下的廣義力Qk，先假設qk不為零，而其它的2個廣義坐標為零，如式（5）所示。

式中，F為機構所受的外力；Δr為動平臺中心的虛位移；G0為動平臺質量；Fk為齒輪拱的驅動力。式（5）兩邊同除以Δqk可得Qk，如式（6）所示。

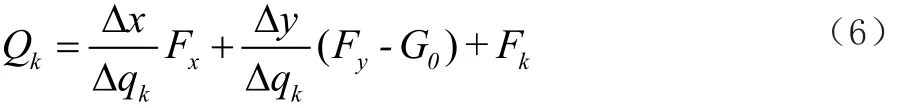
將式（6）寫成矩陣形式，如式（7）所示。

式中,J為Jacobian矩陣。

3 基于Lagrange方法的動力學方程的建立

該雙向偏轉工作臺機構的動能，由動平臺動能和內外兩個齒輪拱兩部分組成,具體表達式如式（8）所示。

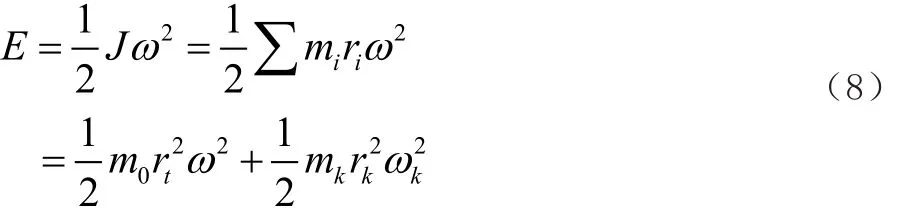
式中，m0為工作臺平臺質量；rt為平臺到轉軸的垂直距離；ωr為平臺轉動角速度；mk為齒輪拱及其導軌副質量；rk為齒輪拱到其轉軸的垂直距離；ωk為齒輪拱轉動角速度。將（8）式兩邊對qk求導，如式（9）所示。

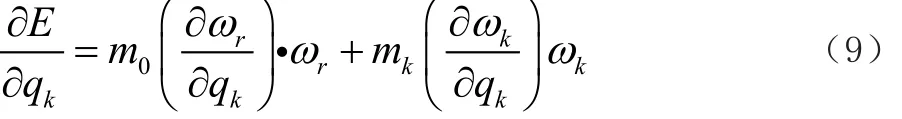
將式（9）對時間t進行求導，如式（10）所示。

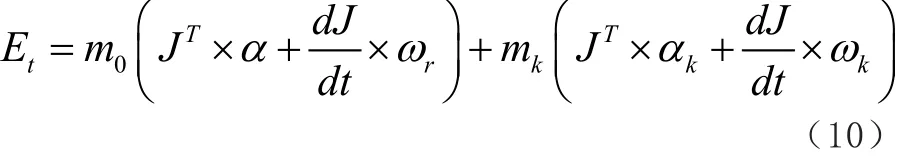
式中，α為動平臺的角加速度；αk為齒輪拱角加速度。將式（7）～式（9）帶入Lagrange方程，如式（11）所示。

可得計算結果，如式（12）所示。

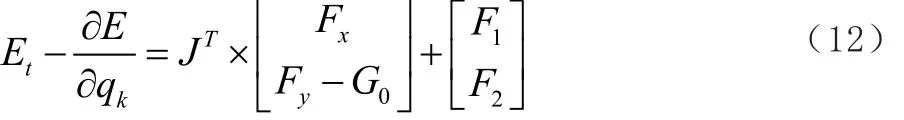
通過式（12）可以得到內外齒輪拱驅動力的大小，并對該機構進行動態特性的分析。

4 并聯雙向偏轉工作臺機構的admas動力學仿真

先將并聯雙向偏轉工作臺模型導入admas軟件之中，并加上各約束后，如圖1所示。

因為兩個消隙齒輪是直接安裝在電機上的，所以當工作臺面加荷載后，測試電機最小驅動力或工作扭矩，可以直接測兩消隙齒輪的驅動力或工作扭矩。測得消隙齒輪驅動力與平臺加入的荷載關系，如圖2所示。

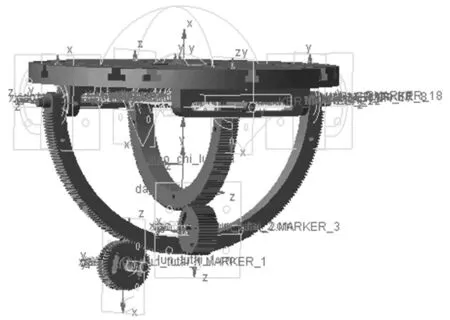
圖1 導入admas中的模型圖

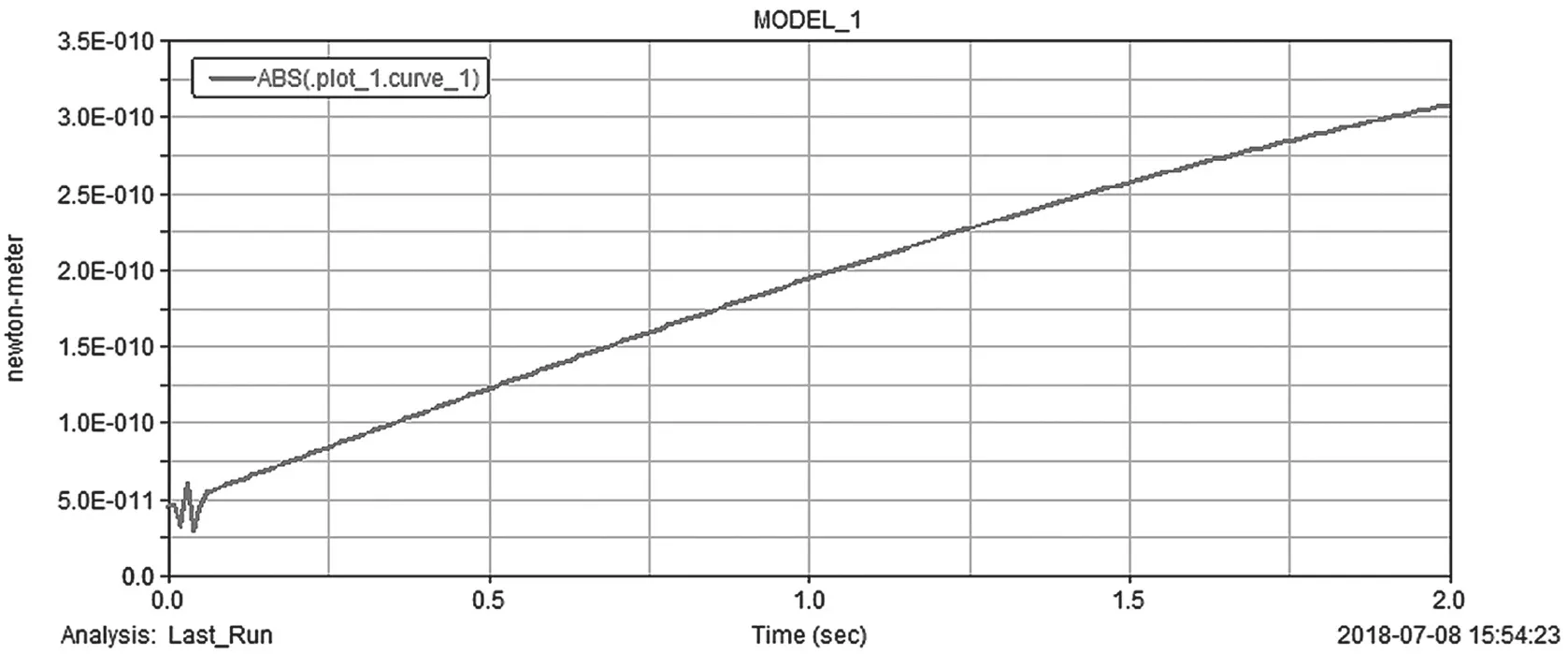
圖2 消隙齒輪驅動力隨運動時間變化圖

如圖（2）所示，當該并聯雙向偏轉工作臺從初始水平位置開始運動后，隨著工作臺的偏轉，工作臺勢能變大，內、外兩驅動電機提供的扭矩也逐漸增大。

5 結語

利用Lagrange方程對該并聯雙向偏轉工作臺進行了動力學模型構建和動力學分析，得到了該工作臺中兩個驅動電機驅動力的顯示解。再利用admas軟件對該工作臺模型進行了動力學仿真與分析，測得了工作臺加載荷載情況下，內、外兩個驅動電機扭矩隨偏轉運動時間變化的關系圖。