某活門最小流量擺動故障分析

楊延麗

（長春科技學院，長春130006）

某型燃油計量裝置在調試過程中出現最小流量波動問題，通過排查故障定位在關斷活門上，因此需要著重分析該活門結構設計對最小流量位置動態及穩態性能影響，從理論上尋找解決該問題的措施。

1 數學模型

1.1 工作原理

關斷活門結構為兩位三通式，彈簧腔通低壓油，控制腔通高壓油。當控制腔燃油壓力逐漸增大并達到活門開啟壓力時，活門打開，控制腔燃油流向發動機，給發動機供油；停車時，通過停車電磁閥控制電控停車活門，活門在彈簧力及高壓油的共同作用下關閉，切斷向發動機供油，實現停車功能[1-4]。

1.2 最小流量穩定點參數

以活門為研究對象，計算最小流量位置活門穩定時，活門受力如式（1）～式（3）所示。

式中，P10為最小流量穩態時的高壓燃油壓力；P0為低壓油壓力；x0為最小流量穩態工作點；AS為閥芯面積；F預為彈簧預緊力；K為彈簧剛度；FS為穩態液動力；kS為穩態液動力系數；ΔP為工作閉鎖活門前后壓差；θ為射流方向角，69°；A(x)為閥套型孔開口面積；L為活門與襯套的遮蓋量；μ為出口流量系數；Cυ為流速系數，0.99。

在x0附近，閥套型孔開口面積如式（4）所示；穩態工作點流量公式如式（5）所示。

式中,Q0為最小流量，kg/h；A0為先導孔的面積。

根據式（1）～式（5）可求得最小流量時活門的穩態工作點，當遮蓋量為0.5mm時，穩態工作點x0為2.8736mm，ΔP為0.124MPa型孔打開面積A(x0)為2.4562mm2，穩態液動力系數kS為1.1328。

1.3 最小流量穩定點處小偏差線性化模型建立

以活門閥芯作為研究對象，根據牛頓第二定律可知活門在穩態工作點附近動力學方程如式（6）所示，結合活門在穩態工作點處的平衡公式（1），系統平衡點附近小偏差線性化表達式如式（7）所示。

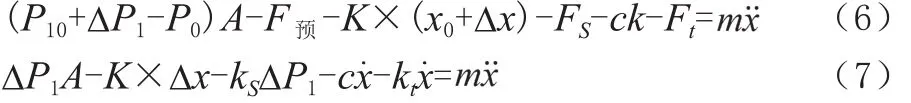
式中，c為阻尼系數；Ft為瞬態液動力；kt為穩態液動力系數；x、、分別為閥芯運動的位移、速度和加速度。

去掉增量符號可得系統在穩態工作點附近小偏差線性化模型，該公式中所有系數均為穩態點處（P10，x0，Q0）(P10,x0,Q0)處對應的常值如式（8）所示。

同理將出口流量方程進行線性化處理，如式（9）所示。

式中，P′10為穩態時閥口后的壓力。

出口流量如式（10）所示；結合式（9）可得增量表達式，去掉增量符號如式（11）所示。

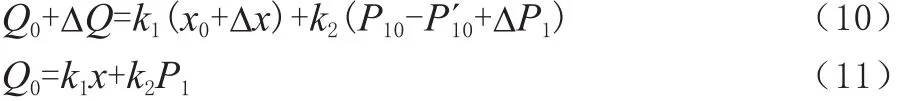
k1、k2表達式如式（12）所示。

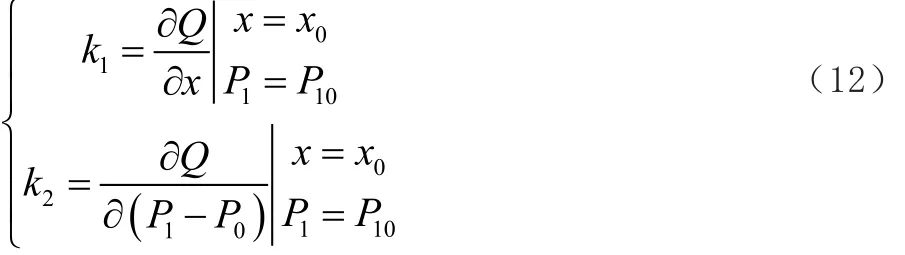
2 穩定性分析及改進措施

系統輸出為流量，系統的輸入為高壓油壓力，由式（8）～式（12）可得系統傳遞函數，如式（13）所示。

由式（13）可知系統為典型的二階系統，系統的特征多項式如式（14）所示。

式中，各個參數均為正值，根據勞斯判據可知系統為穩定系統，系統阻尼比表達式如式（15）所示；系統超調量如式（16）所示。

由式（15）可知，在彈簧剛度及活門閥芯質量、阻尼系數c一定的情況下，系統阻尼比取決于瞬態液動力系數ks大小，根據液壓技術手冊，可知該系數表達式如式（17）所示。

由上式可知，kt隨L變化而變化，增加遮蓋量在一定程度上有助于提高系統阻尼比，進而提高系統的動態特性及穩態性能；將遮蓋量由原來的0.5mm增至2mm，阻尼比增加，系統超調量減小，有助于減小極限環幅值，使得輸出在較小可允許范圍內波動。試驗證明該方法可有效改善最小流量波動問題。

3 結論

本文通過對活門進行受力分析，獲得活門傳遞函數，該傳遞函數中參數包含了活門結構及裝配參數，因此可以從控制理論中系統穩定性及動態特性上分析流量波動原因，因此將流量波動問題轉化為活門結構及裝配因素如何影響阻尼比問題，通過對其影響因素進行分析，對其加以修正并試驗，驗證該可為產品設計提供依據。