曲線擬合算法在光學自準直傳感器設計中的應用
沈廣楠,王曄,李金平,史鑫


摘 要:為了降低光電自準直傳感器的測量誤差,提高傳感器的測量精度,文章從光電自準直傳感器的基本原理出發,介紹了三種不同的曲線擬合算法,通過對光電自準直傳感器樣品進行測試,驗證不同擬合算法對光電自準直的測量誤差的影響,最后對影響光學自準直儀測量精度的因素進行了分析,文章對提高光學自準直傳感器的測量精度具有指導意義。
關鍵詞:光學自準直;誤差分析;角度傳感器;曲線擬合
中圖分類號:TP212 文獻標志碼:A 文章編號:2095-2945(2018)06-0153-02
Abstract: In order to reduce the measurement error of photoelectric autocollimation sensor and improve the measuring accuracy of the sensor, this paper introduces three different curve fitting algorithms based on the basic principle of photoelectric autocollimation sensor. The effect of different fitting algorithms on the measurement error of photoelectric autocollimator is verified by testing the sample of photoelectric autocollimation sensor. Finally, the factors influencing the measurement accuracy of optical autocollimator are analyzed. This paper is of guiding significance for improving the measuring accuracy of optical self-collimating sensor.
Keywords: optical autocollimation; error analysis; angle sensor; curve fitting
引言
光電自準直傳感器是在光學自準直原理的基礎上,結合光電技術將角度測量轉換為線性測量的一種常用技術計量儀器,具有非接觸、小角度多維測量、精度高、方便可靠等優點,被廣泛應用于導軌平臺的直線度、精密平臺的平面度等精密測量領域,在常規測量儀器的制造、測試、科學研究中,尤其是在超精密定位、角度自動定位環集成等方面,更有著無法取代的地位,對于航空航天以及軍事等諸多領域設備的測量標定具有重要意義。
1 光電自準直傳感器基本原理
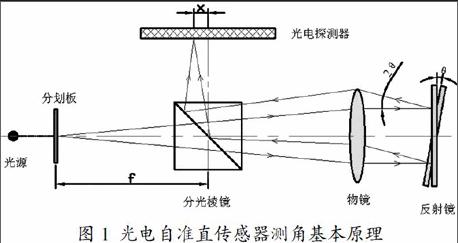
光電自準直傳感器測角基本原理如圖1所示[1-3]。
從光源發出的光,照在位于物鏡的焦平面處的分劃板上[4]。若該點剛好位于物鏡的主光軸上,從該點發出的光經過物鏡后,將平行照射在反射鏡上。若反射鏡垂直于主光軸,光線仍然按原路返回[5]。當反射鏡與光束不垂直,即反射鏡與光軸存在夾角θ時,平行光軸的光線射向反射鏡時,由反射定律可知,反射光線將與原光線成2θ的角度,通過分光棱鏡反射后,光電探測器上的像點產生了x位移偏移量,根據幾何光學的基本原理:x=f·tan2θ,其中:x-返回像的位移偏移量;f-物鏡焦距;θ-反射鏡的偏轉角。當偏轉角θ很小時,tan2θ≈2θ,代入式1,可得:θ=x/2f,其中θ即為待測角度,假設物鏡的焦距f和返回像的位移偏移量x已知,通過式2便得到反射鏡的偏轉角θ。由于在傳感器中物鏡的位置是固定的,其焦距f為一固定常數,因此可通過測量偏移量x 求得θ角的值[6]。
2 試驗驗證
本文根據光電自準直傳感器原理,制作傳感器樣品,傳感器樣品如圖2所示,所用到的設備如下:光電自準直傳感器、計算機、光學分度臺、光學平臺、升降架。試驗環境如圖3所示。光電自準直傳感器測試結果見表1。
對比分段線性插值擬合、高斯擬合、最小二乘法多項式擬合三種不同擬合方式與理論值進行比較。比較結果如4-圖6所示。
通過對比不同擬合方式對光電自準直傳感器的誤差影響可以得到結論:利用最小二乘法多項式進行曲線擬合的方式,與理論值最為接近。對表1數據進行最小二乘法多項式擬合,得到擬合曲線方程為:y=1.29933*10-3x+1.40502*10-3,r2=0.99999,將表2數據代入最小二乘法多項式擬合曲線方程,進行驗證,得到最小二乘法多項式擬合得到的偏移角與由測角儀得到的真實偏移角間的絕對誤差小于20″。在實際產品設計中,光電自準直傳感器的測量誤差不可避免,而影響光電自準直傳感器精度的因素有很多,主要包括光電自準直儀原理誤差、光學系統設計誤差、信號采集與處理系統誤差以及外界干擾誤差、安裝調試誤差等[9]。
4 結束語
本文對光學自準直原理進行了研究,并介紹了幾種不同的擬合算法,利用不同的擬合算法對光學自準直傳感器精度的影響進行了仿真,最后對影響測量精度的因素進行了分析,仿真結果表明,利用曲線擬合算法能夠降低光電自準直傳感器的誤差,而通過對三種不同擬合算法的比較,得到最小二乘法多項式擬合算法與光電自準直傳感器的測量結果更為接近,通過大量數據對最小二乘多項式擬合結果的驗證,絕對誤差小于20″,能夠降低自準直傳感器的測量誤差,從而提高自準直傳感器的測量精度,該算法能夠很好地應用于對實際光電自準直傳感器測試結果的處理。
參考文獻:
[1]黃銀國.激光自準直微小角度測量基礎技術研究[D].天津大學,2009.
[2]王君.光電自準直儀抗背景光干擾技術研究[D].中國科學院大學,2015.
[3]何海霞.基于光電自準直的二維小角度測量技術研究[D].湖北工業大學,2009.
[4]劉學吉,王省書,周金鵬,等.光電自準直系統的建模方法研究[J].半導體光電,2014,37(4).
[5]凌東堯,沈東凱.光電自準直儀關鍵技術研究[J].中國新技術新產品,2014(7).
[6]杜娟,鄭 ,王世鋒,等.激光自準直儀小型化光機結構設計[J].長春理工大學學報,2015,38(6).
[7]李敏,盛毅.高斯擬合算法在光譜建模中的應用研究[J].光譜學與光譜分析,2008,28(10).
[8]丁克良,沈云中,歐吉坤.整體最小二乘法直線擬合[J].遼寧工程技術大學學報(自然科學版),2010,29(01).
[9]張冬,王振宏.PSD光電自準直儀工作原理及誤差分析[J].機械工程師,2014(12).

