星載復雜組件隨機振動試驗載荷設計方法改進

王躍宇，周志成，王 暢

（1.中國空間技術研究院 通信衛星事業部，北京 100094；2.北京聯合大學 旅游學院，北京 100101）

0 引言

隨著移動通信、微波遙感、在軌操作等系統技術的持續發展，對于寬口徑、高增益的大型可展開天線和具有空間感知、機動和操作集成能力的空間機械臂的工程需求越來越多[1-5]。

大型可展開天線、空間機械臂等星（站）載復雜組件在開展結構設計時需要總體部門提供隨機振動設計載荷。而目前已有的隨機振動載荷估算方法在某些加載方向存在預示載荷過分偏離實際載荷的缺陷。隨著以大型可展開天線為代表的星載復雜組件對于減輕重量、提高展開可靠性、實現結構與機構優化設計的需求日益增加，組件結構設計單位迫切希望總體能夠給出既符合實際分布規律，又不過度偏離載荷幅值的載荷設計指標。

為解決組件需求與總體設計指標之間長期以來存在的矛盾，在深入研究國內外已有的隨機振動載荷設計方法的基礎上，本文提出了一種改進的設計方法。該方法既可以給出符合實際分布規律的設計載荷，又具有良好的預示精度，從而為載荷剪裁開拓出一條工程上實用而有效的技術途徑。

1 已有的載荷設計方法

1.1 國外方法

對于復雜組件的隨機振動試驗載荷設計，國外航天器力學環境工程界已率先提出工程可用的載荷預示模型和設計方法，如歐洲ECSS-E-10-03A[6]標準中公布的方法，以下簡稱歐標法（European standard method,ESM）。

ESM實際上是基于2個假設：當組件質量不超過50 kg時，采用切向載荷和法向載荷相異的假設（切法異載假設）；當組件質量大于50 kg時，采用切向載荷和法向載荷相同的假設（各向同載假設）。

ESM 的主要思想是：在沒有可靠的分析結果或其他型號類似組件隨機振動試驗數據可供參考的情況下，假設組件質量為m，按質量大小劃分成為m≤50 kg和m＞50 kg兩個區間，其分別對應的載荷預示模型如表1和表2所示。

表1 ESM載荷譜（m≤50 kg）Table 1 RV test levels of ESM (m≤50 kg)

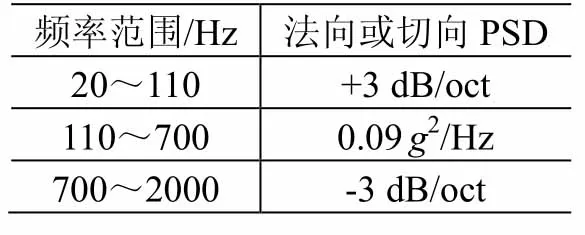
表2 ESM載荷譜（m＞50 kg）Table 2 RV test levels of ESM (m＞50 kg)

1.2 國內方法

盡管受到星載復雜組件數量十分有限、相關試驗數據積累不足等不利條件的阻礙，我國仍堅持開展跟蹤與探索性研究，借鑒國外經驗，針對復雜組件的隨機振動試驗載荷設計提出了衰減因子法（attenuation factor method,AFM）[7]。

AFM 采用的載荷分布假設是各向同載假設。其主要思想是假設組件質量為m，按質量大小劃分為m≤23 kg（甲）、23 kg＜m≤180 kg（乙）和m＞180 kg（丙）3個區間。這3個質量區間分別對應的載荷預示模型如表3所示。

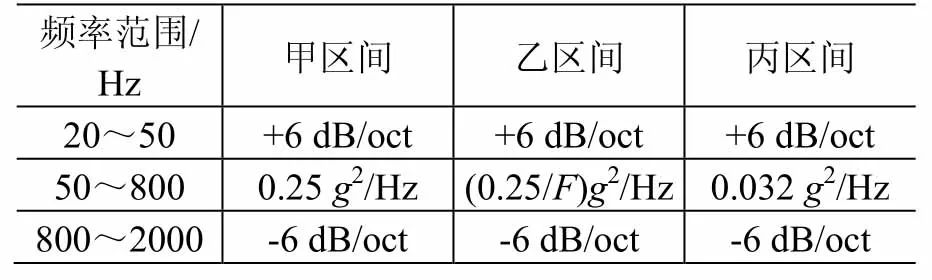
表3 AFM載荷譜Table 3 RV test levels of AFM

1.3 已有方法的局限性

已有設計方法的局限性表現在：1）在部分（例如ESM）或全部（例如AFM）質量區間采用了各向同載假設，忽略了載荷大小對加載方向的敏感性，違背了法向偏大、切向偏小的載荷分布規律；2）由ESM和AFM獲得的載荷（總均方根加速度）預示值往往高于真實載荷，有時甚至高出 2倍以上，會導致復雜組件結構強度的冗余設計；3）ESM有時會給出小于實際載荷的預示結果，無法保證復雜組件載荷設計具有合理的安全裕度。

2 改進的載荷設計方法

為實現結構與機構的優化設計，天線研制部門迫切要求衛星總體設計部門在保證結構安全裕度的前提下，提高載荷預示精度、合理降低設計指標。為此，本文提出了一種改進的復雜組件隨機振動載荷設計方法，簡稱方向質量法（loading direction and mass method,DMM）。其主要思想是：假定組件質量為m，按質量大小劃分成DM01～DM05共5個質量區間，區間范圍依次為m≤23 kg、23 kg＜m≤60 kg、60 kg＜m≤120 kg、120 kg＜m≤180 kg和m＞180 kg。這5個區間的隨機振動試驗載荷譜如表4～表8所示。

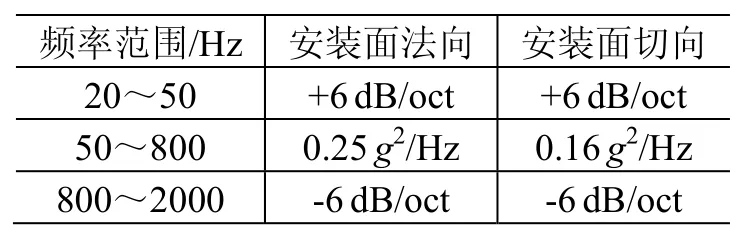
表4 DMM載荷譜（DM01區間）Table 4 RV test levels of DMM (Interval DM01)

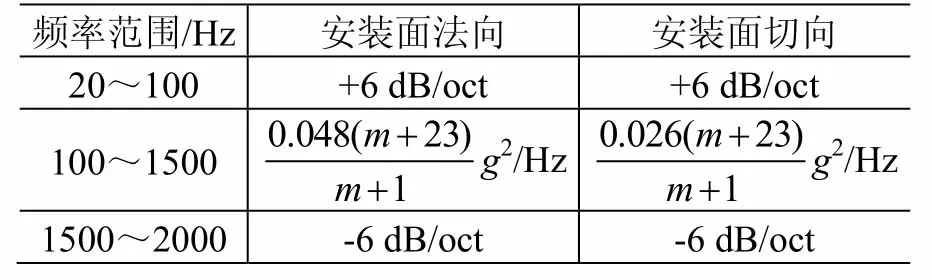
表5 DMM載荷譜（DM02區間）Table 5 RV test levels of DMM (Interval DM02)

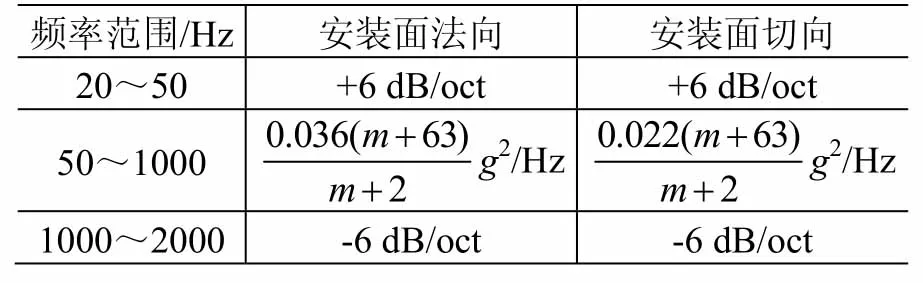
表6 DMM載荷譜（DM03區間）Table 6 RV test levels of DMM (Interval DM03)

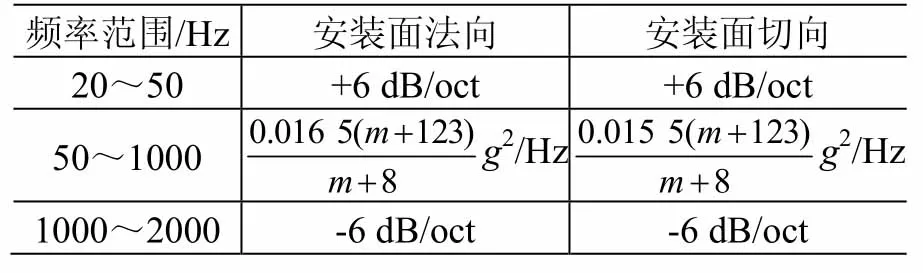
表7 DMM載荷譜（DM04區間）Table 7 RV test levels of DMM (Interval DM04)

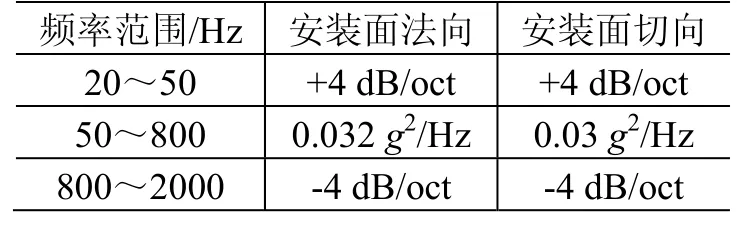
表8 DMM載荷譜（DM05區間）Table 8 RV test levels of DMM (Interval DM05)

DMM 載荷預示模型的建模步驟如下：1）以組件質量m為變量，將隨機振動載荷譜假設為m的分式函數形式，其系數含有待定參數；2）引入載荷偏離度（load deviation,LD）的概念（定義見后），借助數學推導得到待定參數與衛星噪聲試驗實測結果之間的關系式；3）確定待定參數，從而獲得既與組件質量相關，又反映加載實際規律的載荷譜。

下面以質量位于DM02區間，沿安裝面法向加載的隨機振動載荷為例，說明隨機振動載荷預示模型的建模過程。

圖1為隨機振動典型譜，其中，f1～f2頻段為上升譜，f2～f3頻段為平直譜，f3～f4頻段為下降譜。

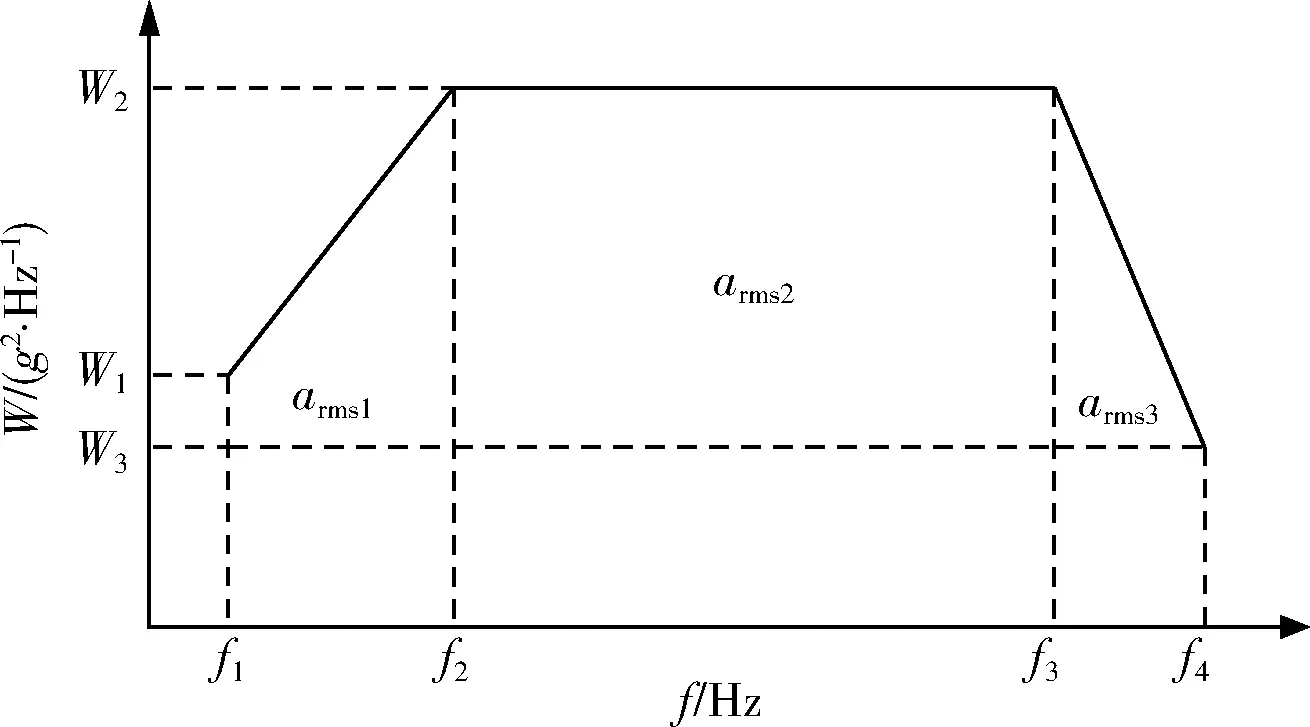
圖1 隨機振動典型譜Fig.1 Typical random vibration spectrum

上升譜的均方加速度為

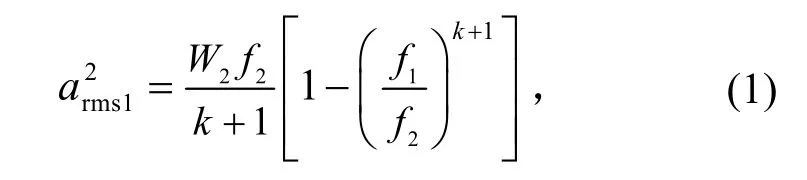
式中：f1和f2分別為上升譜的下、上限頻率；W2為f2和f3處的譜密度；k為1/3倍頻程分貝數。

平直譜的均方加速度為

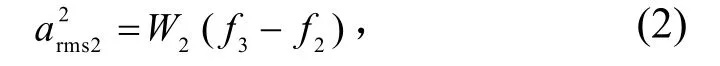
式中，f3為平直譜上限頻率（或下降譜下限頻率）。

下降譜的均方加速度為

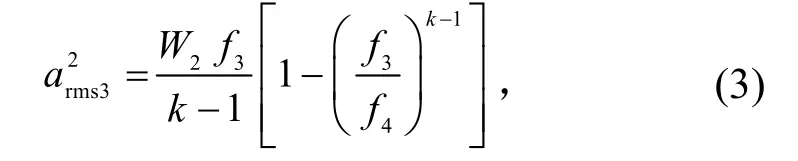
式中，f4為下降譜上限頻率。

隨機振動典型譜的均方根加速度[8]為

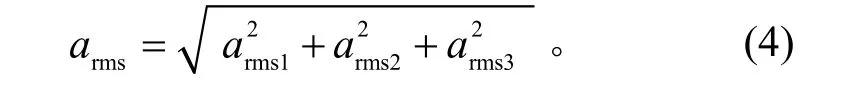
質量位于 DM02區間的天線組件，假設其安裝面法向的隨機振動載荷預示模型為

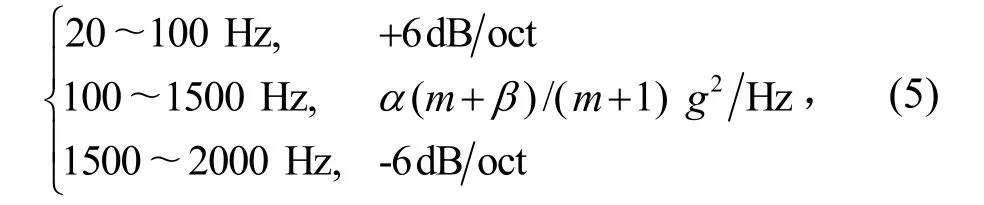
式中，α和β為待定參數。

將式(5)代入式(1)～式(3)，有：

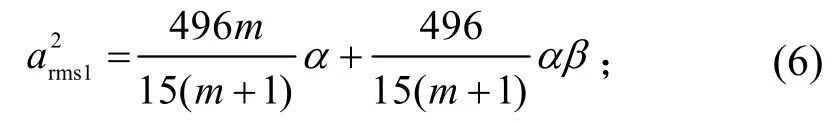
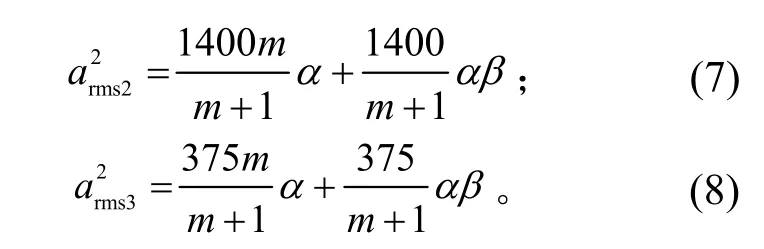
因此，總均方加速度為

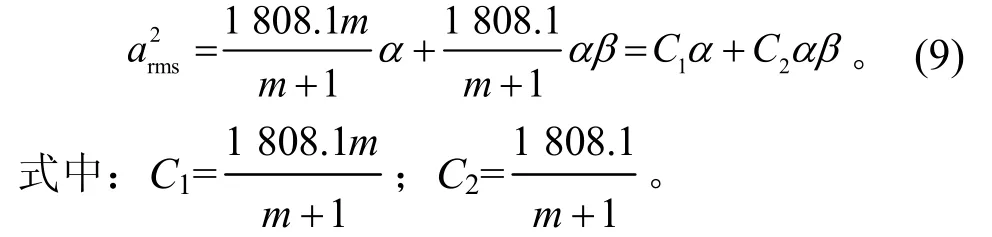
設at-rms為復雜天線組件在衛星噪聲試驗中連接界面處總均方根加速度的實測結果，arms為隨機振動載荷預示模型給出的總均方根加速度，則預示結果的載荷偏離度為LD=[(arms-at-rms)/at-rms]×100%。設 LD=ε，且ε＞0，則有arms=(1+ε)at-rms。將該結果代入式(9)得到C1α+C2αβ=[(1+ε)at-rms]2。一般情況下，按照下限取整原則，β可以取質量區間下限附近的一個整數。這樣，根據at-rms和ε的工程許用值，就可以確定α=[(1+ε)at-rms]2/(C1+C2β)。α和β值一旦確定，即可獲得隨機振動載荷的預示模型。

從內容上看，相對于ESM和AFM，DMM的主要創新體現在將23～180 kg的質量區間細分為3個區間，以衛星噪聲試驗實測數據為依據，分別沿復雜組件安裝面的法向和切向提供全新的載荷設計模型。

3 三種方法的預示精度比較

本文選取了4個典型工程算例：環形天線反射器組件（組件 A）及其饋源組件（組件 B），傘狀天線（組件C），管狀天線（組件D）。各組件質量及其衛星噪聲試驗結果見表9。以LD為指標，利用DMM、ESM和AFM方法可以得到這4個組件的預示精度，詳見表10～表13。

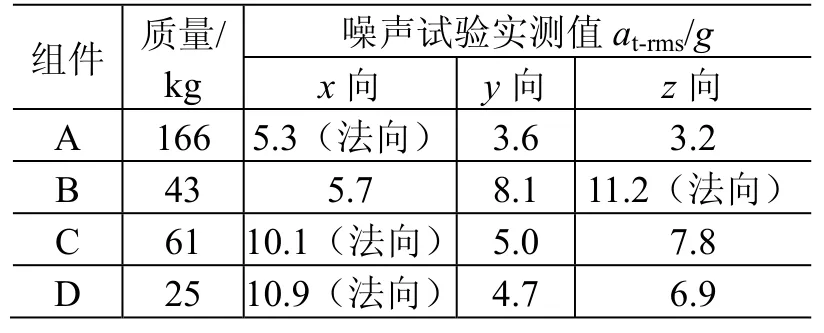
表9 組件質量及其噪聲試驗結果Table 9 Mass and acoustic test results of units

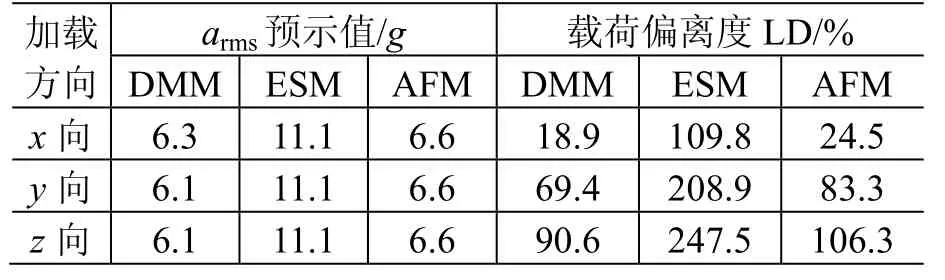
表10 組件A的預示結果及精度Table 10 Prediction results of unit A

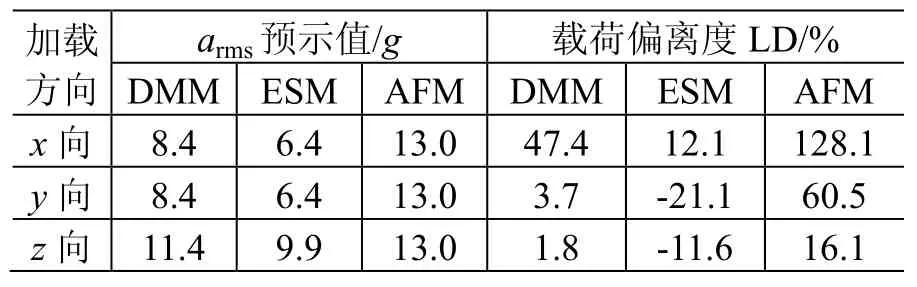
表11 組件B的預示結果及精度Table 11 Prediction results of unit B

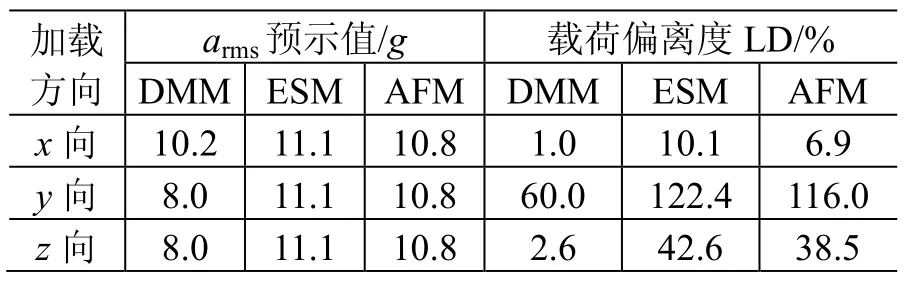
表12 組件C的預示結果及精度Table 12 Prediction results of unit C

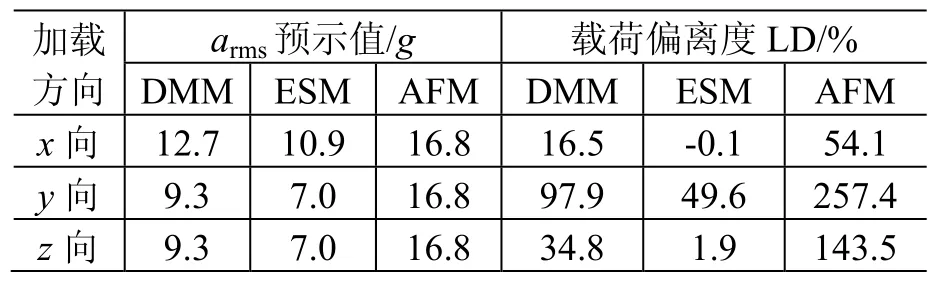
表13 組件D的預示結果及精度Table 13 Prediction results of unit D

觀察表10～表13可知，組件B和組件D的ESM預示載荷偏離度LD出現負值，因此應將其相關數據從統計源中剔除。三種方法的平均誤差參見表14。

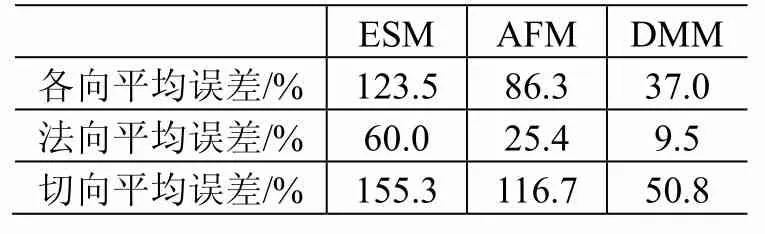
表14 三種方法的預示誤差Table 14 Prediction errors of ESM,AFM and DMM

從表14可看出：和ESM相比，DMM的預示誤差分別減少了70%（各向）、84.1%（法向）、67.3%（切向）；和AFM相比，DMM的預示誤差分別減少了57.1%（各向）、62.5%（法向）、56.5%（切向）。可見，DMM的預示精度明顯高于ESM和AFM，其預示結果最接近衛星噪聲試驗時組件安裝部位的實測結果。

4 結束語

本文針對星載復雜組件隨機振動試驗載荷設計問題提出了一種改進的載荷預示方法（DMM），沿組件安裝面不同加載方向分別提供了隨機振動載荷預示模型，反映了振動載荷隨加載方向變化的實際分布規律，順應了國際環境工程技術的發展潮流。

DMM載荷預示模型的建模思路是以衛星噪聲試驗數據為基礎，通過推導建立預示模型參數與實測物理參數之間的數學關聯。從典型復雜組件隨機振動載荷預示誤差看，ESM和AFM的預示結果有可能與載荷設計要求發生抵觸，這種潛在的風險無疑降低了其工程應用價值。DMM的預示精度明顯優于ESM和AFM，給出的預示載荷最接近衛星噪聲試驗實測結果，可以替代后兩者成為星載復雜組件中高頻段力學環境設計的有力工具。

DMM解決了長期困擾總體載荷設計的一大技術難題，較好地滿足了天線研制單位對隨機振動載荷指標合理剪裁的技術需求，為今后各類星載復雜組件結構與機構優化設計工作的開展創造了有利條件。

（References）

[1]鄔樹楠,劉麗坤,汪銳,等.大型索網式可展開天線在軌高精度指向控制[J].宇航學報,2015,36(10):1140-1147 WU S N,LIU L K,WANG R,et al.On-orbit highaccuracy pointing control for large mesh deployable antenna[J].Journal of Astronautics,2015,36(10): 1140-1147

[2]DATASHVILI L,ENDLER S,WEI B,et al.Study of mechanical architectures of large deployable space antenna apertures: from design to test[J].CEAS Space Journal,2013,5(3): 169-184

[3]王輝,宋燕平,馬小飛.星載大型柔性索網天線重力環境下的型面調試[J].中國空間科學技術,2016,36(4): 33-37 WANG H,SONG Y P,MA X F.Surface accuracy adjusting method of large flexible mesh spaceborne antenna on ground[J].Chinese Space Science and Technology,2016,36(4): 33-37

[4]張華振,馬小飛,宋燕平,等.星載高精度環形網狀天線設計方法[J].中國空間科學技術,2013,33(5): 1-6 ZHANG H Z,MA X F,SONG Y P,et al.Design method of high precision perimeter truss antenna on board[J].Chinese Space Science and Technology,2013,33(5): 1-6

[5]劉宏,蔣再男,劉業超.空間機械臂技術發展綜述[J].載人航天,2015,21(5): 435-443 LIU H,JIANG Z N,LIU Y C.Review of space manipulator technology[J].Manned Spaceflight,2015,21(5): 435-443

[6]Space engineering: testing: ECSS-E-10-03A[S],2002

[7]航天器產品力學環境試驗技術要求: Q/W 1226—2009[S],2009

[8]柯受全,金恂叔.衛星環境工程和模擬試驗[M].北京: 宇航出版社,1996: 56-60