多支持度下用戶行為序列模式挖掘方法研究
徐啟寒 徐開勇 郭 松 戴樂育
(信息工程大學 河南 鄭州 450001)
0 引 言
用戶行為序列模式挖掘是指挖掘出所有滿足指定最小支持度的用戶所有頻繁行為序列的過程,在用戶行為模式分析與用戶輪廓刻畫等方面均具有突出的模式表達能力。
序列模式挖掘最早于1995年由Agrawal等[1]提出。區別于關聯規則挖掘,序列模式挖掘引入時間屬性,具備更強的數據表達能力。除Apriori算法[2]、GSP算法[3]、Prefixspan[4]以及SPAM算法[5]等經典算法外,近幾年以來,一些擴展性更強、挖掘效率更高的方法不斷被提出。Le等[6]通過對候選序列提前剪枝來縮小搜索空間,提出一種高效的挖掘算法STATE-SPADE;Zihayat等[7]提出一種基于內存自適應的HUSP算法MAHUSP,解決數據流更新引起的內存資源限制問題;Kemmar等[8]提出一種前綴投影全局約束方法,壓縮子序列關聯以及頻率約束,解決現有模型約束規模過大問題。
現有研究雖在算法性能和挖掘效果上具有一定的優勢,但由于采用基于單一支持度的支持度閾值設置方式,未考慮用戶自身行為之間的差異性,無法滿足用戶行為模式分析的實際應用需求。在模式挖掘過程中,若支持度閾值設置過高,將導致遺漏發生頻率低但重要性高的操作,影響挖掘結果的準確性。若支持度閾值設置過低,則將導致待挖掘數據規模過大,嚴重影響挖掘效率,同時產生大量對分析無用的冗余信息。所以在用戶行為模式分析中需要采用基于多支持度的模式挖掘方法。
多支持度是指為不同項分別設置不同的最小支持度。該概念最早由Liu等[9]提出,并提出了基于Apriori算法的擴展算法MSApriori。該算法利用向下封閉性來縮減搜索空間,但是很容易導致組合爆炸。文獻[10]提出一種基于MIS-Tree結構的條件頻繁模式增長算法CFP-growth,它通過遞歸地創建條件樹來生成頻繁模式;文獻[11]提出了一種CFP-growth算法的增強算法CFP-growth++,采用壓縮樹結構挖掘頻繁模式;文獻[12]提出一種多最小支持度下基于MapReduce的頻繁模式挖掘框架,挖掘效率更高。
目前現有的基于多支持度的模式挖掘研究多集中在頻繁項集的挖掘上,針對帶有時序屬性的序列模式挖掘研究較少。Liu[13]首次將多最小支持度概念引入序列模式挖掘中,并提出MS-GSP算法。但該算法采用候選序列生成測試的方式,導致運行時間以及內存消耗急劇增加;Huang[14]在挖掘模糊量級序列模式(FQSP)問題中引入多支持度概念及可調整的隸屬度函數,以此來解決單一支持度閾值及單一隸屬度函數所致的實際不可用性問題。
本文以LP-tree結構[15]為基礎,提出一種基于多最小支持度的前綴樹結構MSLP-tree,并進一步提出基于MSLP-tree的序列模式增長算法MSLP-growth。LP-tree是一種線性前綴樹,本文在此基礎上引入多最小支持度等屬性,來解決用戶行為序列模式挖掘中敏感稀有項的問題。在樹的構成上,采用相同前綴序列分枝整合的方法壓縮結構,節約內存空間,并且該結構能夠存儲所有的序列模式,便于序列模式的分析和增量更新的需求。同時,本文所提出的算法無需多次掃描數據庫,不產生候選序列,挖掘效率較高,空間資源消耗較小。
1 用戶行為序列模式相關定義
設I={i1,i2,…,in}為項目的非空集合,集合t?I為項集,項集內各項間無先后順序。序列數據庫S中序列s可記為(sid,s),其中sid為s在S中的標識符。序列s由項集有序排列而成,s可記為s=

表1 示例序列數據庫
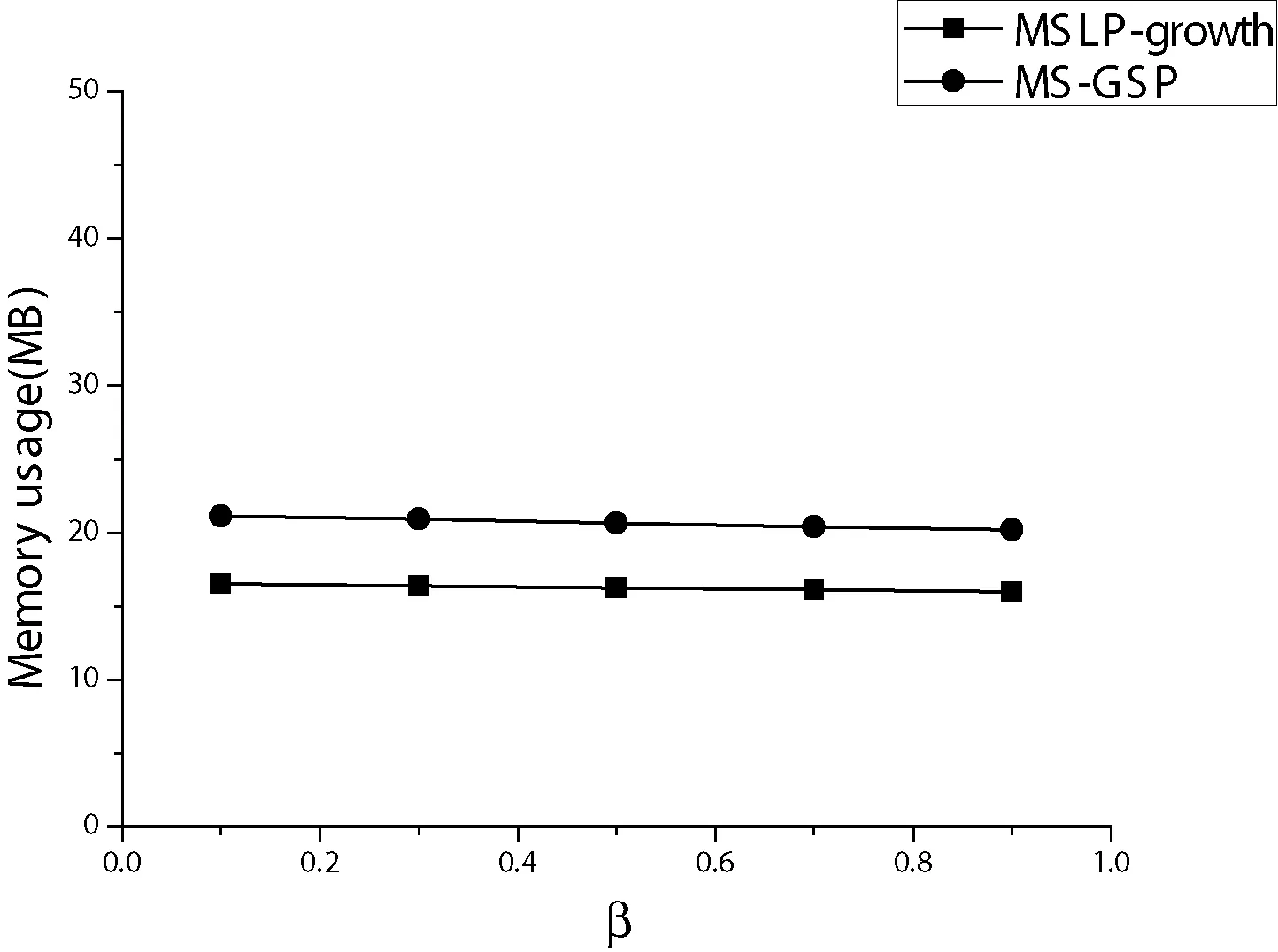
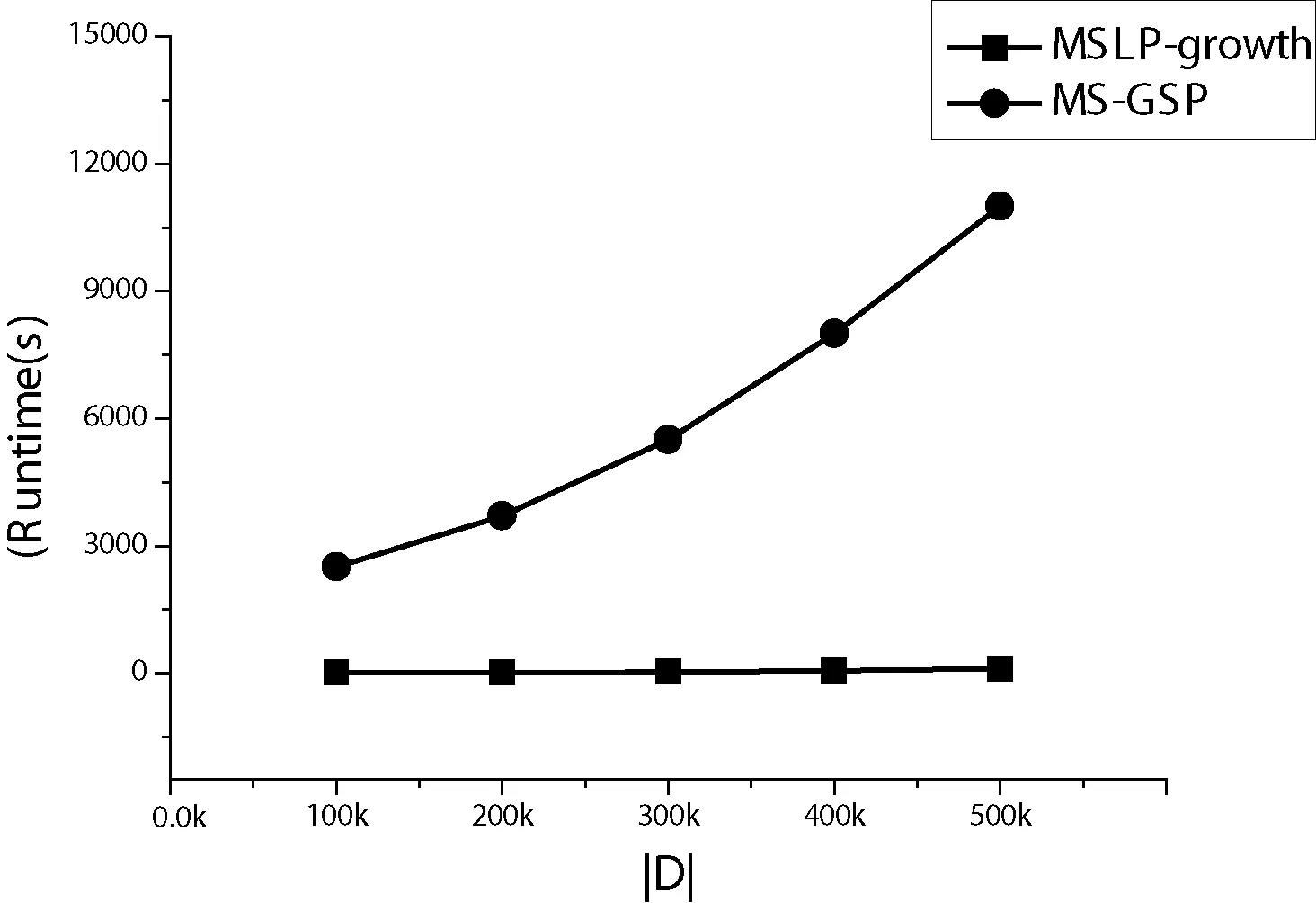
給定序列s1=<α1,α2,…,αn>,序列s2=<β1,β2,…,βm>,n≤m,如果存在1≤j1 定義1支持度。對于序列數據庫S中序列s,s的支持度為S中包含序列s的個數占S中序列總數的比值,記為sup(s)。給定支持度閾值min_sup,如果序列s在S中的支持度不低于min_sup,即sup(s)≥min_sup,則稱序列s為頻繁序列模式。 定義2項集最小支持度。設項目集合I中數據項ij的最小支持度為mis(ij),則I中所有項的最小支持度可記為{mis(i1),mis(i2),…,mis(in)}。對于項集t={i1,i2,…,ik},t?I,項集t的最小支持度記為MIS(t)=min{mis(i1),mis(i2),…,mis(ik)}。表1中各數據項最小支持度如表2所示。 表2 最小支持度表 定義3序列最小支持度。給定序列s= 定義4極小最小支持度。設LMS(least minimum support)為項目集合I中所有項目最小支持度的最小值,則LMS可記為min{mis(i1),mis(i2),…,mis(in)}。 定義5對于任意序列s,如果sup(s)≥MIS(s),則s為頻繁序列或者說s是頻繁的;如果sup(s) 性質1在多支持度下的序列模式中,如果一個序列是不頻繁的,但它的超序列可能是頻繁的。 性質2對于序列模式X和Y,X?Y,如果sup(X) 本節首先描述MSLP-tree的結構,然后介紹構造過程。 MSLP-tree主要由四部分構成,包括根節點Root、頭表Header List、樹節點LPNc以及枝節點信息表BNL: 1) 根節點標記為Root,值為空。 2) 頭表(Header List)中主要包括四個屬性:數據項名稱item.name、支持度support、數據項最小支持度mis、連接具有相同名稱數據項節點之間的連接點node.link。 3) 樹節點LPN(Liner Prefix Node)內節點存儲頻繁項信息,包括數據項名稱item.name、該項支持度support、序列當前最小支持度值mis、連接點node.link以及枝節點信息branch information。其中,各LPN內首節點為該LPN表頭,用以連接其父節點;LPN結構組成可表示為LPN={ 4) 枝節點表BNL(Branch Node List)包括各枝節點及其對應各子節點信息。BNL表示為BNL={{B1→C1,1,C1,2,…,C1,j},{B2→C2,1,C2,2,…,C2,j},…,{Bi→Ci,1,Ci,2,…,Ci,j}},Bi為第i個枝節點指針,Ci,j為Bi第j個子節點指針。設Pc,k為LPN內某一節點的指針,它表示LPNc第k個節點的指針,PRoot為指向根節點的指針。 綜上,MSLP-tree可記為MSLP-tree={Header List,BNL,LPN1,LPN2,…,LPNc}形式,其中c為樹中LPN的總個數。MSLP-tree的結構示例如圖1所示。 圖1 MSLP-tree結構 MSLP-tree構造流程如算法1。具體構造過程如下: Step1掃描序列數據庫S(其中所有序列已按最小支持度值升序排列),找出所有數據項i,并對其進行支持度計數,將支持度小于LMS的項刪除,所有滿足LMS模式的項記入頭表中,并按mis升序排列。 Step2在樹中插入第一個序列,序列首項記為ik,長度為1。若某一項i為項集擴展項,則在該項前添加符號“_”,記為_i。各項按序列中順序依次記入LPN中,各項支持度計數+1,記為LPN1。LPN1內部節點的個數為序列長度+1,即包括LPN1表頭。將LPN1與根節點相連,LPN1內首節點指針指向根節點Root,P1,1→PRoot。此時生成BNL,BNL(PRoot)→BNL(Pc,1)。 Step3繼續將數據庫其他序列插入樹中,數據處理同Step2。此時分三種情況,若新序列與樹中已插入序列LPNc前k項相同,則將前k項插入LPNc中,其余n-k項生成新LPN,LPNc前k項支持度+1,LPNnew首項即原序列第k+1項,且Pnew,k+1→Pc,k,BNL(Pc,k)→BNL(Pnew,k+1);若新插入序列與樹中已插入序列首項均不同,則將序列所有項記入新LPN中,此時根節點產生新子節點,Pnew,1→PRoot,BNL(PRoot)→BNL(Pnew,1);若新序列所有項與已插入序列前k項相同,則將原序列前k項支持度+1,自第k+1項移出生成新LPN,Pnew,1→Pc,k,BNL(Pc,k)→BNL(Pnew,1)。 Step4記LPN內節點為qc,k,將所有LPN中具有子節點的內節點的“branch information”記為“true”,否則記為“false”。將所有同名稱項節點自node.link起始鏈接,若無節點間連接信息node.link位記為null,BNL信息依據LPN連接情況補充完整。 至此,MSLP-tree構造完畢。 算法1MSLP-tree構造算法 輸入:序列數據庫S,數據項集合I,項目最小支持度表,極小最小支持度LMS 輸出:MSLP-tree Step1 1) 掃描序列數據庫S,找出所有數據項i; 2) Generate Root; //創建樹的根節點 3) For each itemiinI; 4) Count the support ofi; //對i進行支持度計數; 5) If sup(ij) //刪除非LMS模式項 6) end if; 7) Create Header List; //生成頭表,數據項按MIS升序排列; 8) end for; Step2 9) For each itemiins; 10)ik←first item,l←the length; //ik為s首項,l為s長度 11) end for; 12) 在樹中插入序列s,記為LPNc; 13) If i is an extension item,i=_i; //i為項集擴展,在i前添加“_” 14)Pc,kS++; //各項支持度+1 15) Link theLPNcwith Root; 16)PRoot←Pc,1; 17) Generate BNL; //生成BNL; 18)BNL(PRoot)→BNL(Pc,1); //將PRoot記入branch node list中,Pc,1記入child node list中; 19) end if; Step3 20) Insert next sequence; //繼續將剩余序列插入樹中 21) Ifik=Pc,k,ik?Snew,Pc,1?BNL(PRoot), //新序列中前k項與LPNc中前k項相同 22) ThenPc,kS++; //LPNc前k項支持度各+1 23) GenerateLPNnew,ik+1=Pnew,1; //序列第k+1項為LPN首項,序列長度為l=n-k+1 24)Pc,k←Pnew,1; 25)BNL(Pc,k)→BNL(Pnew,1); 26) Else ifi1≠Pc,1,i1?Snew,Pc,1?BNL(PRoot); //新序列的第1項和Root所有子節點均不等 27) GenerateLPNnew; //生成新LPN 28)Pnew,kS++; 29)PRoot←Pnew,1; 30)BNL(Pc,k)→BNL(Pnew,1); 31) Else ifin=Pc,k,k≠n,in?Snew,Pc,k?BNL(PRoot); //如果新序列的所有項與LPNc前k項相同 32)Pc,kS++; //LPNc前k項支持度+1 33) Remove the restn-kitem ofLPNcas the newLPN; 34)Pnew,kS++; 35)Pc,k←Pnew,1; 36)BNL(Pc,k)→BNL(Pnew,1); 37) end if; 38) Go to line 17 for next sequence ; Step4 39) ifqc,k有子節點,thenb=true; 40) elseb=false; 41) link all nodes with same name; //將相同名稱節點相連 42) Ifqhas no link, then node.link=null; 43) end if; 44) Return tree 對于表1中序列,其MSLP-tree構建過程如下: 1) 掃描數據庫S,找出所有項并對各項支持度進行計數,其中a=4,b=4,c=3,d=3,e=3,f=3,g=1;根據表2中各項最小支持度值,LMS=0.3,sup(g) 2) 構建樹的根節點Root,將序列s1= 3) 將序列s2=<(ad)c(bc)(ae)>插入樹中,檢查序列中各項均在頭表中,其與s1具有相同前綴a,故將”_d”作為a的子節點,構造新的LPN,新的LPN首節點為”_d”,其指針指向LPN1中節點a,同時節點a支持度加1,將所有項按在序列中的順序依次記入LPN2中,LPN2中各節點支持度記為1;在BNL中,將P1,1記錄到枝節點表中,P2,1記錄到子節點表中,BNL(P1,1)→BNL(P2,1),LPN2表頭記為P1,1。 4) 將序列s3=<(ef)(ab)(df)cb>插入樹中,s3中各項均在頭表項中,s3與s1具有不同前綴,創建新的LPN,將各項按順序記入LPN中,新LPN3內首節點項為e,其指針P3,1指向根節點Root,LPN3中所有節點支持度記為1;在BNL中,將P3,1添加到PRoot對應的子節點表中,BNL(PRoot)→BNL(P3,1),LPN3表頭記為PRoot。 5) 將序列s4= 6)S中所有序列插入完畢,頭表中自node.Link起始,鏈接所有名稱相同項,各LPN內節點屬性信息node.link及branch information補充完整,至此,MSLP-tree構造完畢。前綴樹的最終結構如圖2所示。 圖2 示例前綴樹 基于MSLP-tree結構,序列數據庫中所有序列都可以在樹中找到其唯一路徑,且樹中只存在所有滿足mis和LMS模式的項。對于所有滿足最小支持度條件的序列模式,根據頭表node.link鏈接信息,遍歷整個MSLP-tree,即可得到所有符合支持度要求的模式。在MSLP-tree的構建過程中,將序列重合部分進行分枝整合,能夠壓縮樹的結構,減少路徑遍歷次數。同時可以提前過濾不可能成為頻繁項的信息,從而減少中間冗余信息。 樹的遍歷過程采用深度優先方式,從根節點開始依次遍歷所有節點。首先,找到當前節點的所有子節點,以及所有與其同名項;然后,通過子節點以及相同項找到該路徑下在樹中最后一個節點;最后,遍歷所有的子節點及其兄弟節點,直到不再有未遍歷的節點。 算法主要思想是將不同前綴項下的所有路徑劃分于不同搜索空間進行挖掘。由于該項條件下的前綴樹結構已包含所有該項的條件序列,故可挖掘出所有符合最小支持度條件的完整的序列模式的集合。挖掘過程如算法2。 記K={k1,k2,…,kn}為頻繁序列模式集合,ki(1≤i≤n)為頻繁模式,ki= 首先,從頭表中第一項開始,由node.link信息找到所有同名項進行支持度計數,其中,i與_i分別計數,同一序列中具有相同前綴項不重復計數。根據當前計數以及當前最小支持度值與模式判斷條件相比較,滿足sup≥LMS且sup≥mis的輸出到K中,并以i為條件前綴繼續在i的前綴樹中挖掘;滿足sup≥LMS但不滿足sup≥mis條件的予以保留以待繼續挖掘其可能存在的頻繁超序列模式;對于不滿足sup≥LMS的,不再繼續挖掘。 其次,對于存在后綴以及子節點的模式,記i′為i在附加某一i之后的超序列,記R為前綴集合,將i′記入R中。對i′繼續挖掘,對所有i′模式進行支持度計數,計數方式同i。根據當前計數及最小支持度值,判斷是否為頻繁模式,若當前i′模式仍有后綴模式存在,則照此法繼續挖掘;若已無超序列模式,則對當前前綴項終止挖掘。 最后,將頭表中所有項按以上步驟遞歸挖掘。 算法2MSLP-growth算法 輸入:MSLP-tree結構,Header List,LMS 輸出:頻繁序列模式集K Step1 1) For each i in Header List; 2) For each node q,q.name=i.name; //q為i的node.link鏈接同名項 3) Count support of q; 4) If同一序列中有多個q,then只做一次計數; 5) Count q and _q separately; 6) If sup(q)≥LMS and sup(q)≥mis, //mis為當前m值 7) Then output q; 8) If q有后綴節點或子節點; 9) Put q into R; //R為前綴根節點集合 10) If sup(q)≥LMS,but sup(q)≥mis,then retain q; 11) If sup(q) Step2 12) For q in R; 13) Append i after q as q′; 14) Count support of q′; 15) If sup(q′)≥LMS and sup(q′)≥mis; 16) Then output q′ into K; 17) If q′有后綴節點或子節點; 18) Put q′ into R; 19) If sup(q′)≥LMS but sup(q′)≥mis,then retain q′; 20) If sup(q′) 21) If q′沒有超序列,then stop mining; 22) Output q′ into K; Step3 23) Loop until there is no prefix node exist; 24) End; 本文的實驗平臺為Intel(R)Core(TM)i7-4790處理器,CPU3.6 GHz,2.0 GB運行內存,64位windows 7操作系統。算法采用C++語言實現,編譯環境Visual C++6.0。實驗數據采用IBM公司數據生成器生成的標準數據集[1]。數據集相關參數設置如下:D為客戶數;T為客戶平均事務數;I為事務平均項數,設為2.5;N為項數,設為10 000;L為最大頻繁序列平均長度,設為4。 本文采用文獻[9]中提出的多最小支持度設置方法,定義各項mis值取為: mis(ij)=max{βf(ij),LMS} 式中:β為常量,取值范圍為[0,1];f(ij)為各項的頻率函數,即各項的支持度;LMS為設定的極小最小支持度。當β=0時,mis(ij)=LMS,即所有項最小支持度相同,皆為LMS;當β=1時,由于f(ij)≥LMS,所以mis(ij)=f(ij)。 實驗首先對LMS值固定、β值改變的情況下,MSLP-growth算法和MS-GSP算法的性能進行比較。兩算法的執行時間與內存消耗對比結果分別如圖3及圖4所示。 圖3 算法執行時間比較(LMS=0.015,D=100×103,T=10) 圖4 算法空間消耗比較(LMS=0.015,D=100×103,T=10) 如圖3所示,MSLP-growth算法的執行時間明顯低于MS-GSP算法。這是因為MS-GSP算法在執行過程中產生大量的候選序列,導致算法的執行時間更長。MSLP-growth算法由于不需要生成候選序列,而是采用“邊挖掘邊檢驗”的策略,在挖掘中即生成頻繁模式,而且對于那些不會產生頻繁超序列的前綴模式不再繼續挖掘,節省了大量不必要的運算時間。隨著β值的增大,滿足條件的模式數量逐漸減少,MSLP-growth算法和MS-GSP算法的執行時間都相對縮短,但MSLP-growth算法性能仍然高于MS-GSP算法。 圖4描述了MSLP-growth算法和MS-GSP算法的內存消耗對比結果。從圖4中可以看出,本文所提出的MSLP-growth算法具有較小的內存消耗。這是因為MSLP-growth算法采用線性結構,并且采用分枝整合策略實現MSLP-tree的最大化壓縮。同時在挖掘前刪除大量的非頻繁項,從而有效降低內存使用量。 在算法可擴展性測試中,設定LMS與β為0.025和0.5,客戶數量D從100×103到500×103,每次增加100×103,兩算法的執行時間對比結果如圖5所示。可以發現,隨著數據集容量逐漸變大,MSLP-growth算法的運算時間趨于穩定,而MS-GSP算法的執行時間則顯著增加。由以上分析可知,MSLP-growth算法具有良好的可擴展性。 圖5 算法執行時間比較(LMS=0.025,β=0.5,T=10) 綜上分析,無論是在以支持度閾值為條件變量,還是在不同容量數據集環境下,本文所提出的MSLP-growth算法都表現出優越的性能。 本文針對現有主流序列模式挖掘算法無法有效滿足用戶行為模式挖掘的應用需求,提出一種基于前綴樹結構的多支持度序列模式挖掘方法。通過為序列中各項設置不同最小支持度,解決了單一支持度閾值下行為模式挖掘的準確度和效率過低的問題。實驗結果表明了本文所提算法的高效性和良好的可擴展性。下一步工作將進一步討論多最小支持度下算法優化問題以及不同項目權重對用戶行為模式生成結果的影響。 [1] Agrawal R,Srikant R.Mining sequential patterns[C]//Eleventh International Conference on Data Engineering.IEEE Xplore,1995:3-14. [2] Srikant R,Agrawal R.Mining Sequential Patterns:Generalizations and Performance Improvements[C]//International Conference on Extending Database Technology:Advances in Database Technology.Springer-Verlag,1996:3-17. [3] Zaki M J.SPADE:an efficient algorithm for mining frequent sequences[J].Machine Learning,2001,42(1):31-60. [4] Pei J,Han J,Mortazavi-Asl B,et al.PrefixSpan:Mining Sequential Patterns Efficiently by Prefix-Projected Pattern Growth[C]//International Conference on Data Engineering.IEEE Computer Society,2001:215. [5] Ayres J,Flannick J,Gehrke J,et al.Sequential PAttern mining using a bitmap representation[C]//Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2002:429-435. [6] Le B,Tran MT,Tran D.A method for early pruning a branch of candidates in the process of mining sequential patterns[C]//Intelligent Information and Database Systems.ACIIDS 2017.Lecture Notes in Computer Science,Springer,2017,vol 10191. [7] Zihayat M,Chen Y,An A.Memory-adaptive high utility sequential pattern mining over data streams[J].Machine Learning,2017,106(6):799-836. [8] Kemmar A,Lebbah Y,Loudni S,et al.Prefix-projection global constraint and top- k,approach for sequential pattern mining[J].Constraints,2017,22(2):265-306. [9] Liu B,Hsu W,Ma Y.Mining association rules with multiple minimum supports[C]//Proceeding of the 5th International Conference on Knowledge Discovery and Data Mining,San Diego,CA,USA.1999. [10] Hu Y H,Chen Y L.Mining association rules with multiple minimum supports:a new mining algorithm and a support tuning mechanism[J].Decision Support Systems,2006,42(1):1-24. [11] Kiran R U,Reddy P K.Novel techniques to reduce search space in multiple minimum supports-based frequent pattern mining algorithms[C]//International Conference on Extending Database Technology.ACM,2011:11-20. [12] Wang C S,Lin S L,Chang J Y.MapReduce-Based frequent pattern mining framework with multiple item support[C]//Intelligent Information and Database Systems.ACIIDS 2017.Lecture Notes in Computer Science,Springer,2017,vol 10192. [13] Liu B.Web data mining:exploring hyperlinks,Contents,and Usage Data[M].Springer-Verlag Berlin Heidelberg,2007:41-45. [14] Huang C K.Discovery of fuzzy quantitative sequential patterns with multiple minimum supports and adjustable membership functions[J].Information Sciences,2013,222(3):126-146. [15] Pyun G,Yun U,Ryu K H.Efficient frequent pattern mining based on Linear Prefix tree[J].Knowledge-Based Systems,2014,55:125-139.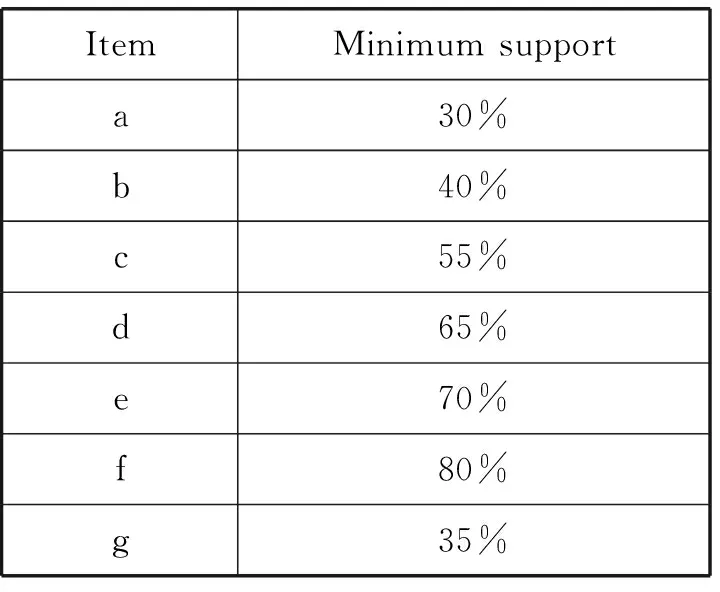
2 MSLP-tree
2.1 MSLP-tree結構
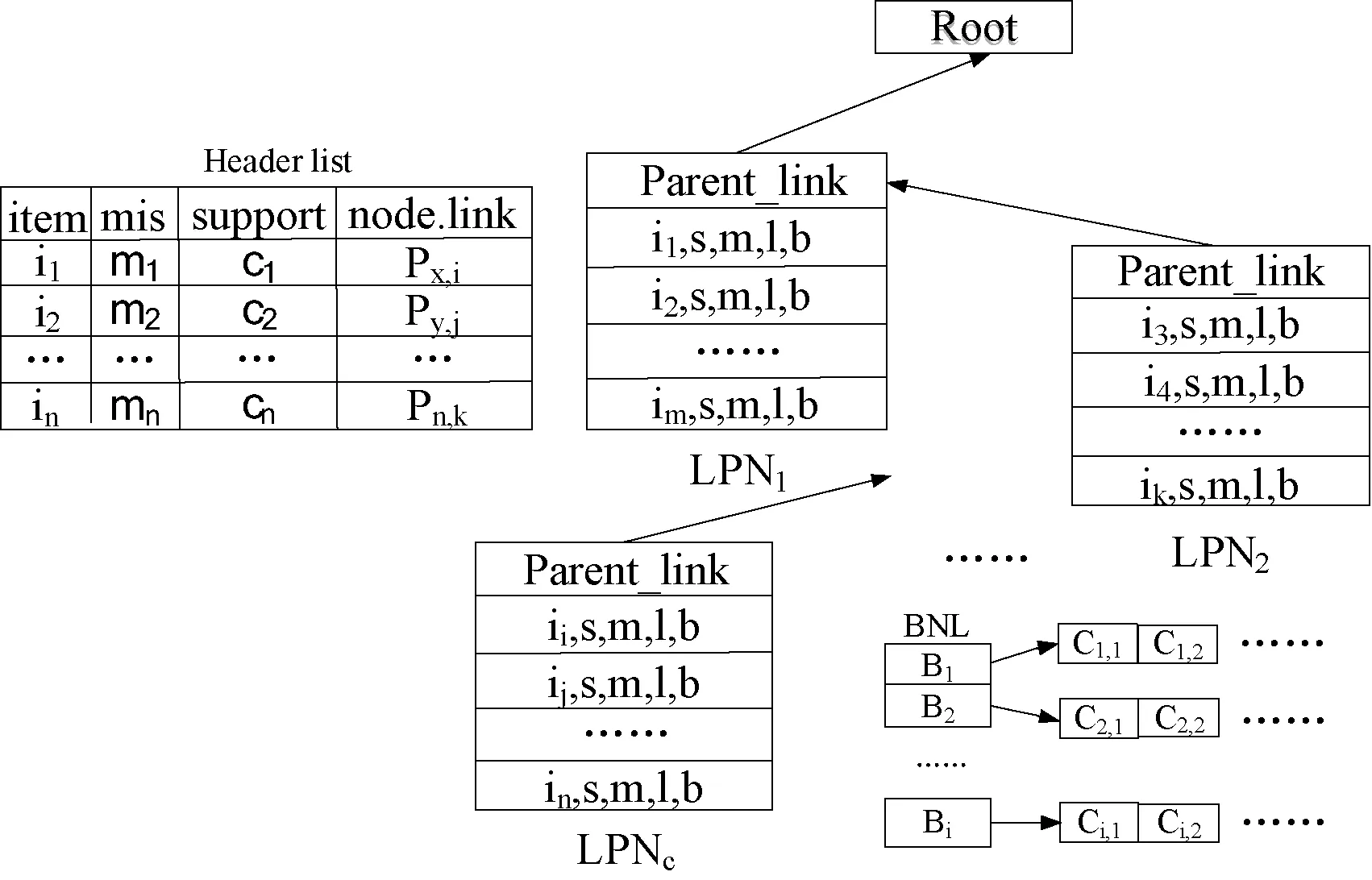
2.2 構造MSLP-tree
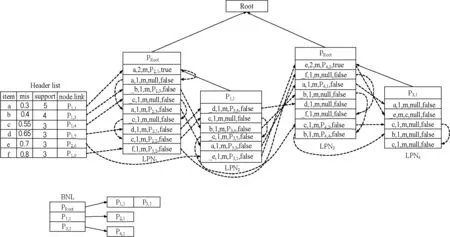
3 MSLP-growth算法
4 仿真實驗及結果分析
4.1 性能測試
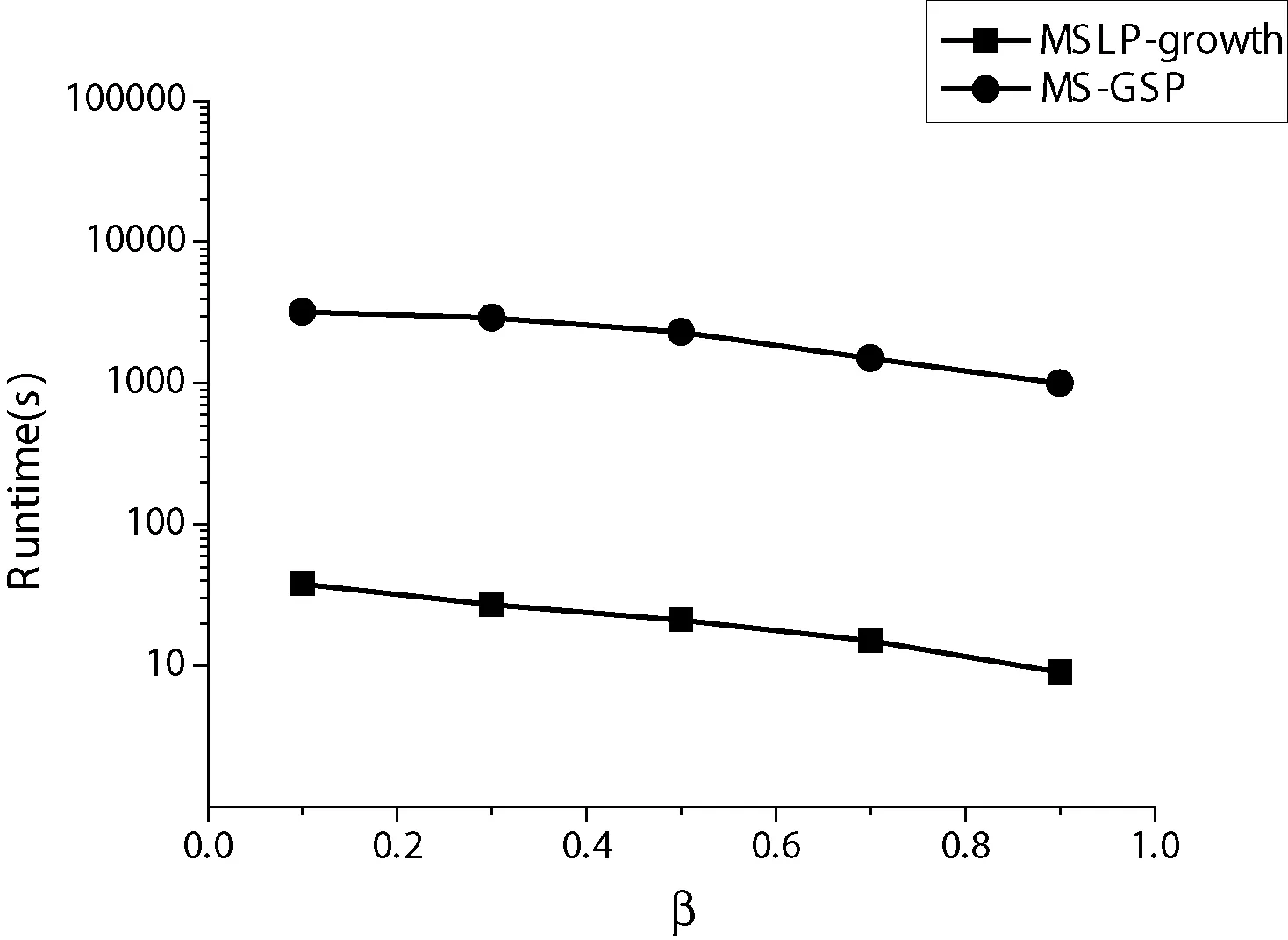
4.2 可擴展性測試
5 結 語

