含裂紋故障的航空發動機轉子系統動力學特性分析

路振勇, 侯 磊, 侯升亮, 陳予恕, 孫傳宗

(1.哈爾濱工業大學 航天學院,哈爾濱 150001;2.山東師范大學 管理科學與工程學院,濟南 250014)

轉軸裂紋故障是航空發動機、燃氣輪機等大型旋轉機械的常見故障之一[1]，裂紋的出現對系統的危害極大。二十世紀七十年代，Gasch[2]提出鉸鏈彈簧模型來研究簡單實心軸裂紋轉子的振動特性，Mayes等[3]研究裂紋轉子的剛度模型時提出用余弦函數來模擬裂紋的開閉效應。迄今國內外學者圍繞著轉軸裂紋的剛度模型、裂紋的檢測診斷識別、裂紋轉子的非線性動力學特性、裂紋轉子的實驗研究等方向開展了大量工作。林言麗等[4]研究了裂紋轉子的剛度問題，并提出了能更好地反映裂紋轉子的剛度變化的應力強度因子為零法。王仲生等[5]研究了裂紋信號的提取、診斷和識別問題，指出倍頻成分是裂紋轉子的常伴頻率；王國彪等[6]從小波有限元裂紋動態定量診斷等方面對裂紋轉子的研究進行了全面綜述。程禮等[7-8]研究了裂紋對轉子系統臨界轉速的影響，指出裂紋會減小系統的剛度降低臨界轉速，同時會激起亞臨界轉速的共振。文獻[9-10]研究了非線性油膜力支承下裂紋轉子的穩定性、混沌等現象，Han等[11]研究了雙裂紋轉子的穩定性問題，Hou等[12-14]研究了機動飛行環境下裂紋轉子系統的非線性動力學特性，于海等[15]研究了高維裂紋轉子系統的動力學降維問題。

軸裂紋轉子系統的研究關鍵在于剛度的求解。大部分研究對象都是軸裂紋位于圓盤根部的Jeffcott模型，忽略陀螺效應，從斷裂力學角度出發，求解裂紋局部附加柔度，進而求解裂紋轉子剛度。但該方法模型過于簡單，無法研究裂紋位于不同位置的情況。Al-Shudeifat等[16-19]認為裂紋隨著系統旋轉會開閉，考慮了較為精確的呼吸開關函數，建立了求解裂紋剛度的有限元模型；然后考慮重力占優及不平衡激勵，對實心軸橫向裂紋轉子的有限元建模、動力學求解分析及裂紋實驗等方面做了大量工作。這些有限元研究方法適用于裂紋位于任意位置的情況，但是其對象是實心軸裂紋轉子，軸段采用Rayleigh梁-軸模型。

為了提高效率，航空發動機一般采用雙轉子結構，高壓轉子為相對短粗型的空心軸轉子。但目前為止，人們對空心軸裂紋轉子系統的研究不多，文獻[20-21]對空心軸常開裂紋轉子和雙轉子裂紋系統的動力學特性進行了分析。本文以某航空發動機高壓轉子為研究對象，建立了含有橫向弓形呼吸裂紋的單跨雙盤有限元模型，推導了空心Timoshenko梁-軸裂紋轉子系統的剛度矩陣，基于有限元法建立了系統的運動方程，采用諧波平衡法分析了系統的非線性響應等動力學特性，并用Newmark-β方法進行了數值驗證。

1 空心軸呼吸裂紋轉子系統建模

1.1 航空發動機高壓轉子-空心軸裂紋系統模型

某航空發動機高壓轉子系統，由多級壓氣機輪盤和一級渦輪輪盤、空心轉軸和支承單元組成；轉子為剛性連接，支承在兩個支點上；轉子支承形式采用1-0-1支承方案。假定在空心轉軸某位置存在一橫向裂紋，系統的有限元動力學模型如圖1所示，模型共分成13個節點、12個軸段單元，集中后的壓氣機輪盤位于節點4，渦輪輪盤位于節點10。

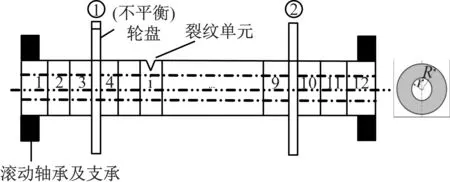
圖1 裂紋轉子簡化系統有限元模型

1.2 空心軸裂紋單元剛度矩陣推導

對于大型旋轉機械系統，裂紋轉子在重力占優等情況下，裂紋截面是時而張開時而閉合的“呼吸模式”。轉子旋轉過程中，裂紋面隨轉角的變化而周期性開閉，用開關函數來模擬裂紋的張開和閉合規律，本文中選取文獻分析中常用的余弦模型

(1)

式中:Ω為轉子旋轉的速度，開閉規律見圖2。

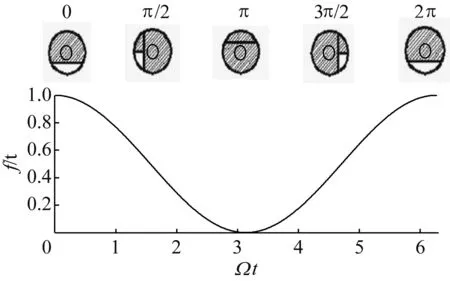
圖2 裂紋截面余弦開閉規律圖

裂紋截面圖及坐標如圖3所示，對于空心軸裂紋轉子系統，裂紋截面分為裂紋貫穿內環和裂紋非貫穿內環兩種情況。

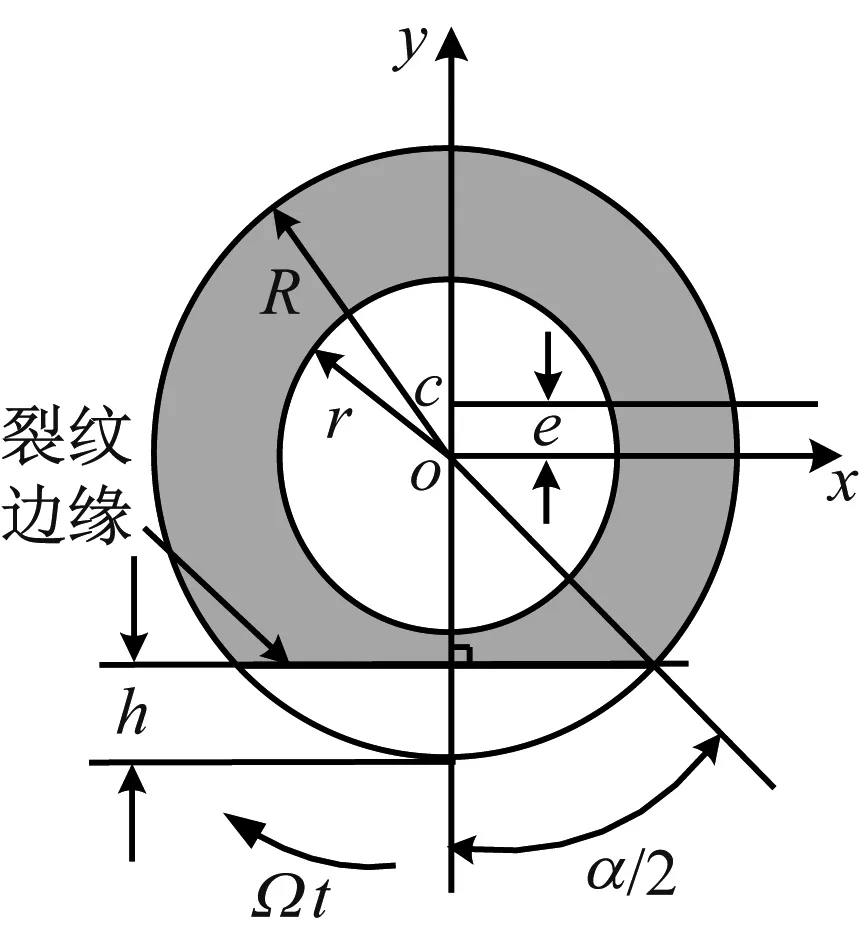
(a) 未貫穿

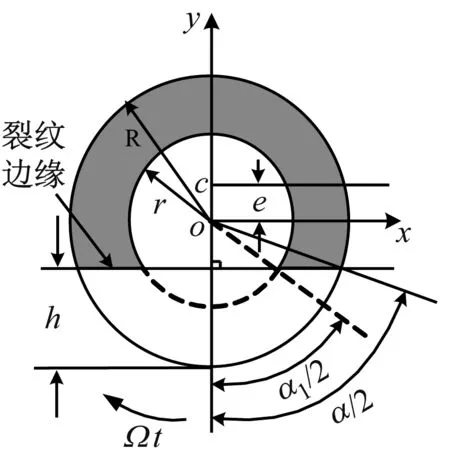
(b) 貫穿情況

圖3中陰影部分表示未開裂部分。o-xy為固定坐標系，ox和oy分別為垂直和平行于裂紋方向。o為不含裂紋時截面的中心，c為出現裂紋后截面的中心，e=oc為中心位置的變化量，h為裂紋的深度，φ為裂紋初始位置角(本文取0)，Ω為轉子旋轉速度，R為外半徑，r為內半徑，α為外圓環開裂時的裂紋角，α1為內圓環開裂時的裂紋角。

本文中假定裂紋截面對固定坐標軸的截面慣性矩隨著旋轉角度的變化不變，即認為當裂紋深度一定時，裂紋截面兩個方向的慣性矩也為定值，但裂紋截面的形心(質心)會因為裂紋的產生而變化。裂紋部分對坐標軸ox和oy的慣性矩、裂紋單元剩余面積Ace、形心距離e及裂紋角α為

(2)

Ace=R2(π-cos-1(1-μ)+(1-μ)γ)-πr2

(3)

(4)

α=2arcos(1-μ)

(5)

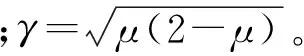
除去裂紋部分，剩余部分對過新的形心軸cx和cy的慣性矩為

I=π(R4/4-r4/4)

(6)

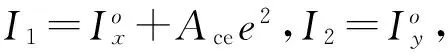
(7)

對于裂紋貫穿內壁情況有

(8)

Ace=R2(π-cos-1(1-μ)+(1-μ)γ)-

(9)

(10)

α1=2arcos((R-h)/r)

(11)

當R=2，r=1時，圖4給出了無量綱裂紋深度從0變化到半徑深度時I1、I2的變化量。可知隨著裂紋加深，兩個方向上慣性矩減小量均增加，且增加量不相同。

圖4 慣性矩減小量隨裂紋深度的變化

Fig.4 The reduction in the moment of inertias of the cracked element versusμ

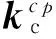
(12)

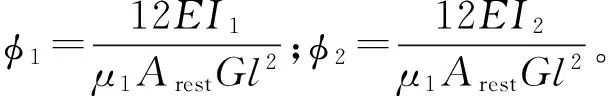
對于裂紋單元，新的剛度矩陣可寫成

(13)

式中:kcp為無裂紋時單元cp的剛度矩陣，代入開關函數，我們有裂紋單元的剛度矩陣隨著旋轉角度的變化為

(14)

1.3 滾動軸承及支承組件線性化模型

根據航空發動機手冊[22]，滾動軸承及支承組合系統可視為兩個串聯的彈簧，如圖5所示。

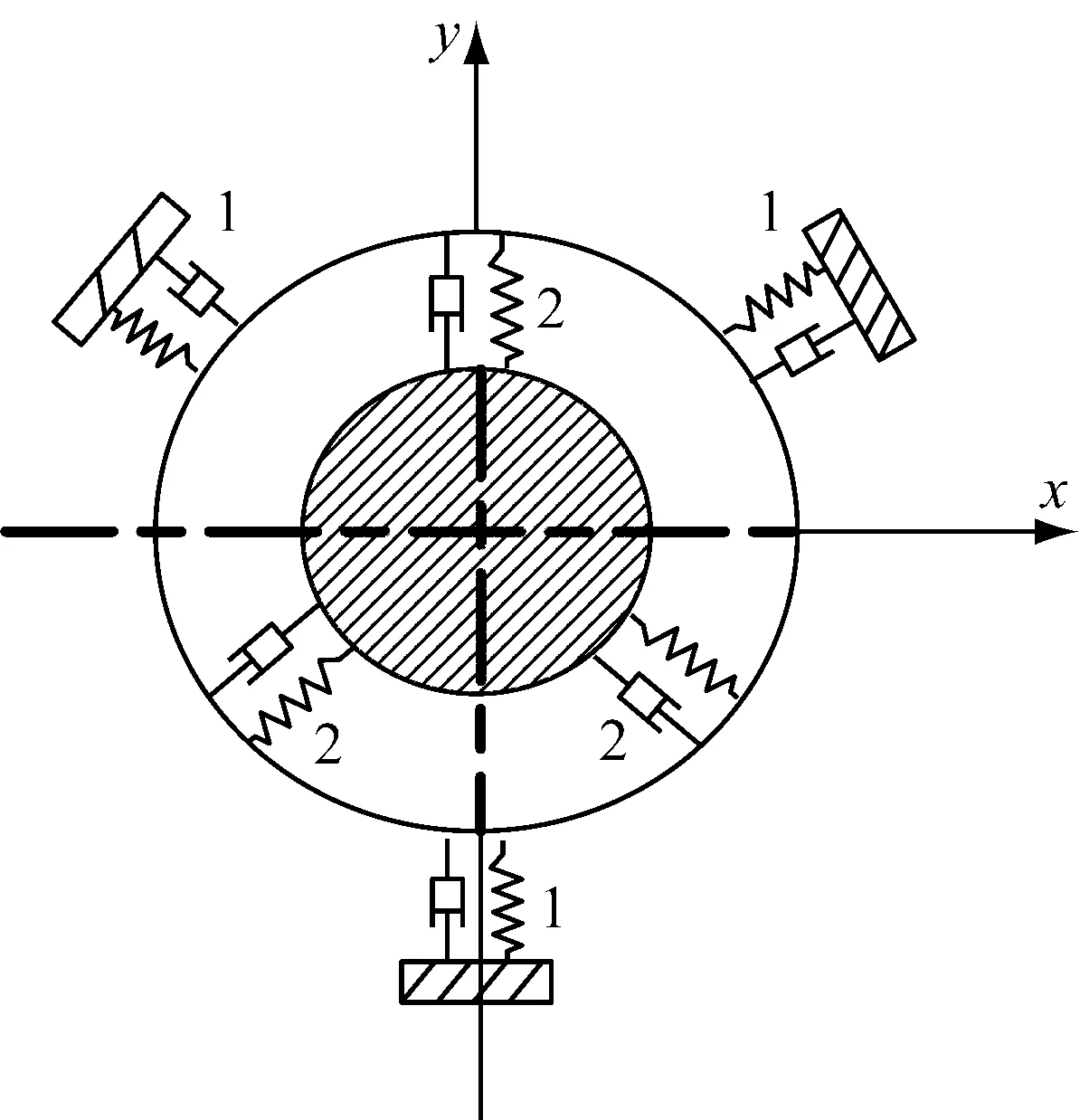
圖5 軸承及支承組件剛度計算示意圖

圖5中，1為支承組件，2為滾動軸承，滾動軸承和支承組件的組合剛度為

(15)

式中:k為軸承與支承組合件的線性化組合剛度;k1為支承組件的線性化剛度;k2為滾動軸承的線性化剛度。滾動軸承及支承組件的阻尼可以同理得到。

1.4 系統動力學方程

根據轉子動力學有限元法[23]，考慮呼吸裂紋因素，

裂紋轉子的動力學微分方程為

F1cos(Ωt)+F2sin(Ωt)+Fg

(16)

代入裂紋開關函數式(1)可得

F1cos(Ωt)+F2sin(Ωt)+Fg

(17)

2 方程求解

根據諧波平衡法[24]，設方程式(17)的解為

(18)

式中:k=1,2,…,n為諧波次數，本文中取n=4。代入系統的運動微分方程式(17)可得

(19)

確定系統的各項參數后，根據式(19)求得A0、Ak、Bk(k=1,2,…,n)，即可求得系統各點的穩態響應，繼而分析空心軸呼吸裂紋轉子系統的動力學特性。

3 計算結果與分析

根據式(19)，計算了含有橫向空心軸呼吸裂紋轉子系統的非線性動力學特性。軸段采用Timoshenko梁-空心軸，裂紋轉子有限元模型是不對稱的系統，集中簡化后的壓氣機圓盤約為渦輪圓盤質量的1.83倍；僅在圓盤①處有不平衡量，空心軸內外半徑比r/R≈0.97。計算時取四次諧波分量。下述情況取不平衡偏角和不平衡量為β=0，med=5×10-2kg·m，支承阻尼為1 000 Ns/m，裂紋初始位置角φ=0，由計算可得，對于無裂紋的線性轉子系統，一、二階同向臨界轉速為ωf1=912.9 rad/s和ωf2=2 054.5 rad/s，一、二階反向臨界轉速為ωb1=850.8 rad/s和ωb2=1 785.7 rad/s。

圖6給出了裂紋位于單元7、節點4處的無量綱裂紋深度-旋轉速度-幅值三維瀑布圖，圖7給出了μ=0，μ=0.5，μ=0.9三種情況下節點4處亞臨界轉速范圍內的幅值-轉速圖。分析圖6可知，隨著裂紋的產生及擴展，系統在一階臨界轉速(同向和反向)處以及臨界轉速的1/2，1/3，1/4附近均會出現峰值，一階臨界轉速大小隨著裂紋深度增加略有減小；結合圖7可知，裂紋轉子系統在1/2，1/3，1/4臨界轉速附近的響應峰值隨著裂紋的出現及加深而明顯增加。總之，裂紋出現后，幅頻圖中臨界轉速和1/n(n=2，3，4)倍臨界轉速附近會出現峰值，這是裂紋存在的一個動力學特征。

圖6 無量綱裂紋深度-旋轉速度-幅值三維瀑布圖

Fig.6 Waterfall of the shaft for non-dimensional crack depthμ, rotational speedΩand vibration amplitude

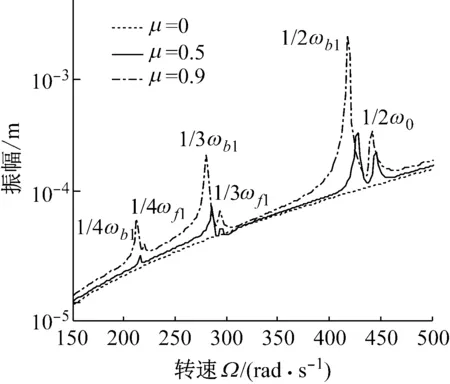
圖7 不同無量裂紋深度下轉速-幅值圖

Fig.7 Vibration amplitudes of node 5 for the subcritical rotational speedΩwith different values ofμ

圖8給出了裂紋存在于不同位置(單元1、單元3和單元7)，μ=0.75時節點4處亞臨界轉速范圍內的幅值-轉速圖。分析圖8可知，裂紋位于單元1支承端附近時，1/n(n=2，3，4)倍臨界轉速附近的幅值較小，裂紋信號較弱；裂紋位于單元3靠近壓氣機輪盤時，1/n(n=2，3，4)倍臨界轉速處峰值明顯出現；裂紋位于單元7在軸段中間時，1/n(n=2，3，4)倍臨界轉速處峰值明顯增大。可知，軸段中間位置出現裂紋時對系統的動力學響應影響較大。Al-shude fat等的研究結果也印證了這一規律。

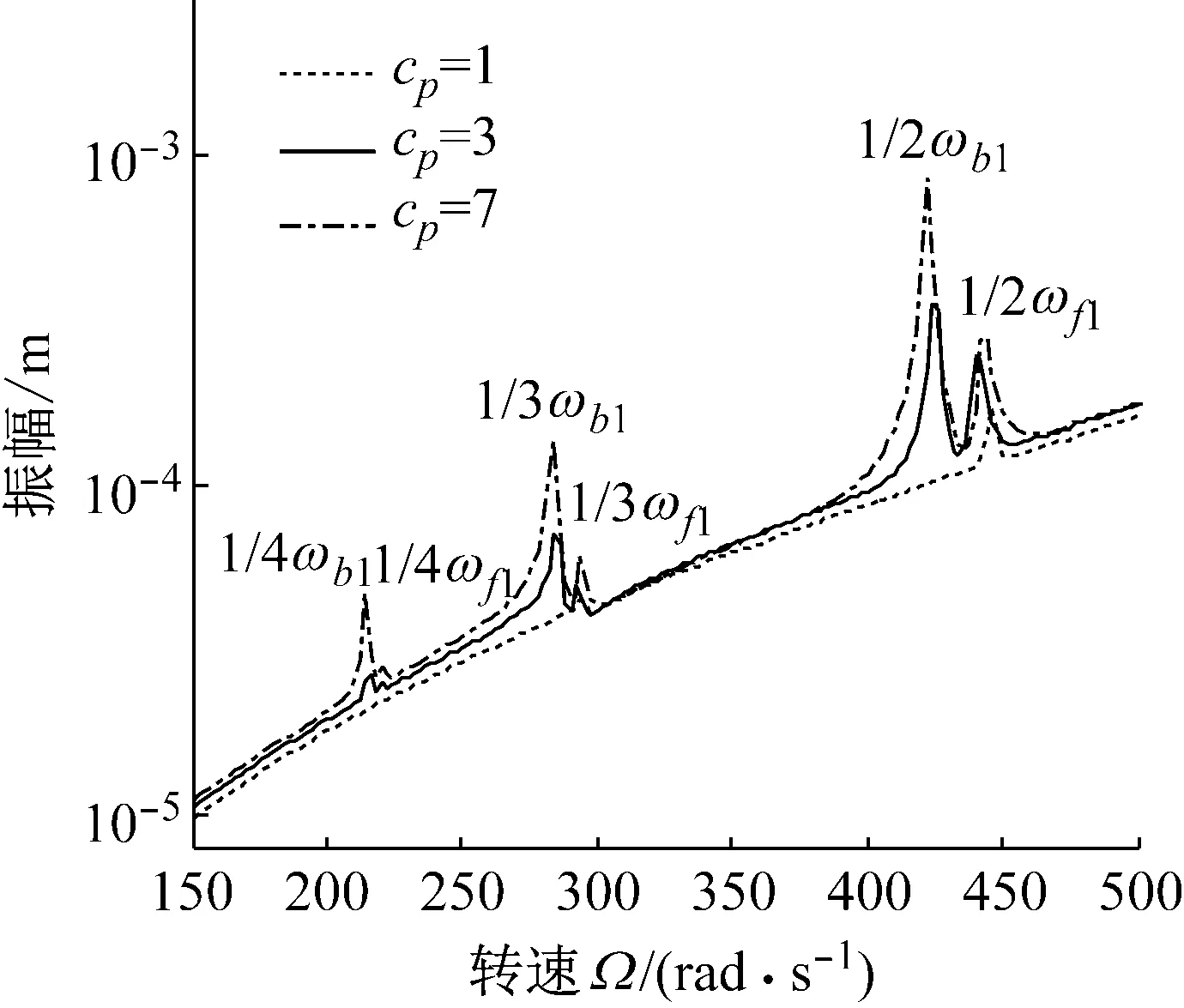
圖8 不同裂紋位置下轉速-幅值圖

Fig.8 Vibration amplitudes of node 5 for the subcritical rotational speedΩwith different positions of the crackcp

圖9給出了裂紋位于單元7，μ=0.7時節點4處升速過程中的三維頻譜圖。分析圖9，在升速過程中，系統響應成分以基頻為主，同時出現明顯的2X、3X、4X倍頻成分，尤其以2X、3X成分為顯著特征。

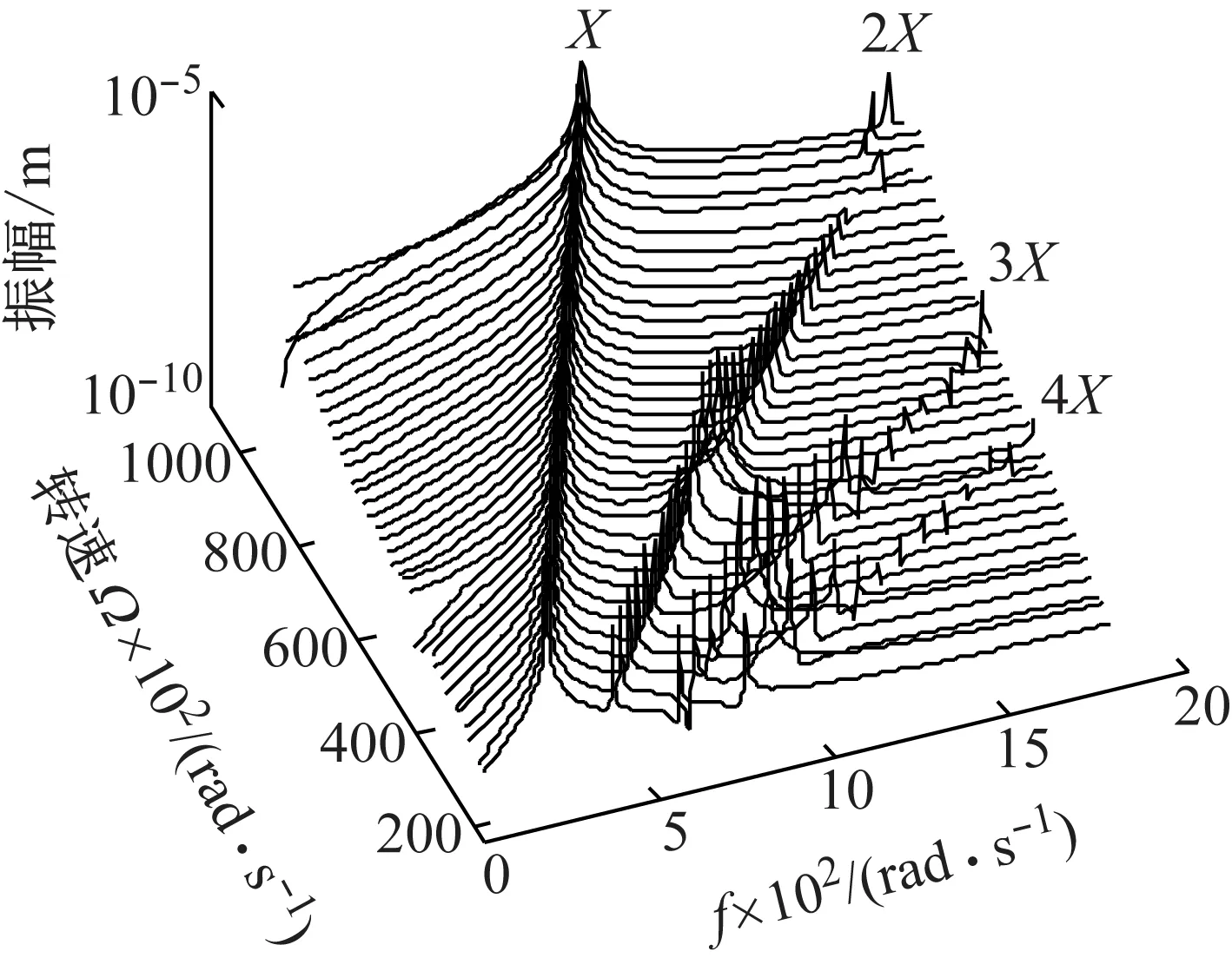
圖9 三維頻譜圖

4 數值驗證

本節用Newmark-β計算方法計算方程式(17)的數值解響應，與諧波平衡法的求解結果進行對比分析。圖10給出了裂紋位于單元7、μ=0.7、Ω=600 rad/s時節點4處的響應結果對比圖。分析可知，裂紋轉子系統在Ω=600 rad/s非共振轉速下，應用諧波平衡法取4次諧波得到的響應和應用Newmark-β數值計算得到的結果完全吻合。此外，非共振轉速下系統的軸心軌跡是一個橢圓，頻譜圖中成分以基頻成分1X為主，倍頻成分出現，但不占優。

圖11給出了裂紋位于單元7、μ=0.7、Ω=425 rad/s≈1/2ωb1時節點4處的響應結果對比圖。分析可知，裂紋轉子系統在1/2臨界轉速附近Ω=425 rad/s時(此時發生2階超諧共振)，應用諧波平衡法取4次諧波得到的響應與應用Newmark-β數值計算得到的結果基本一致。同時，系統的軸心軌跡表現為2個疊加的橢圓，頻譜圖中成分表現為二倍頻成分2X占優，基頻成分1X次之，三倍頻成分3X和四倍頻成分4X相對較小。

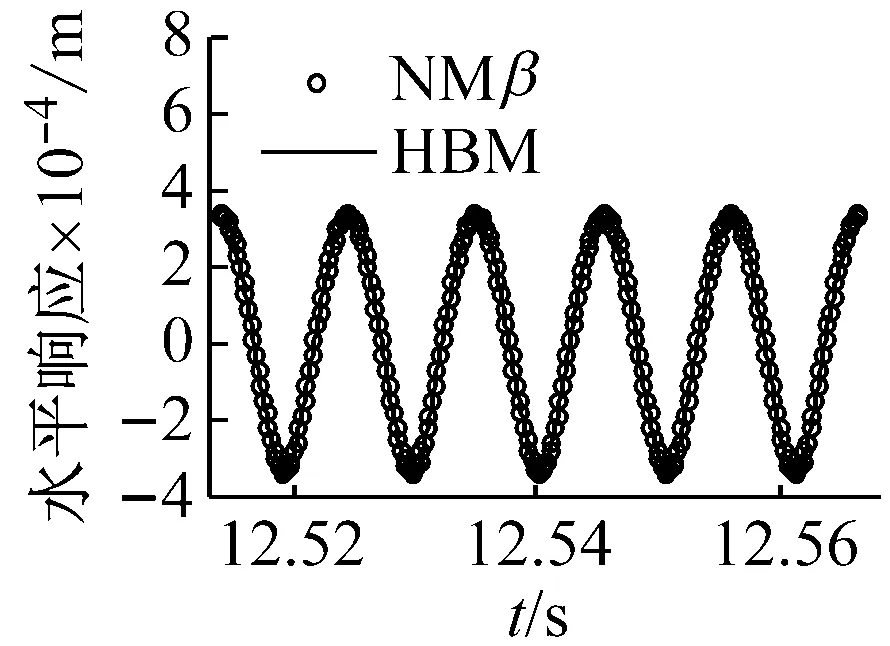
(a) 水平方向時間歷程

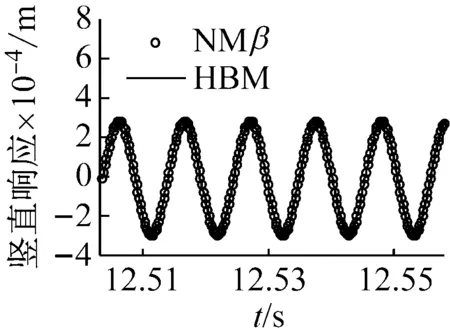
(b) 豎直方向時間歷程

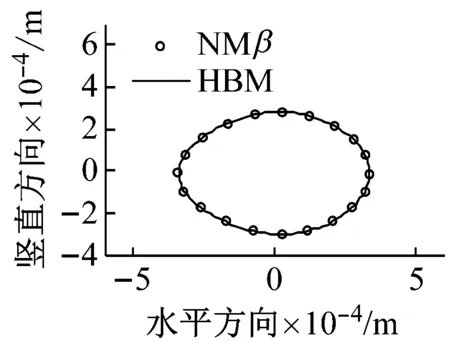
(c) 軸心軌跡圖

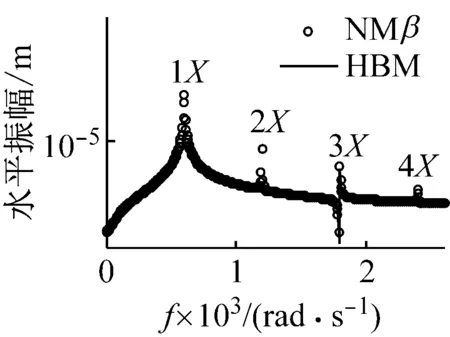
(d) 水平方向頻譜圖

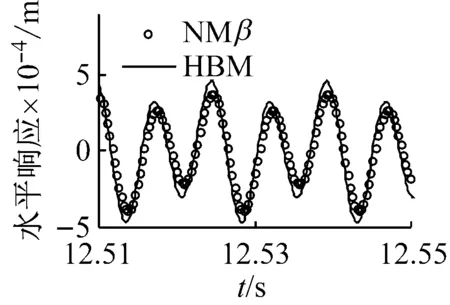
(a) 水平方向時間歷程

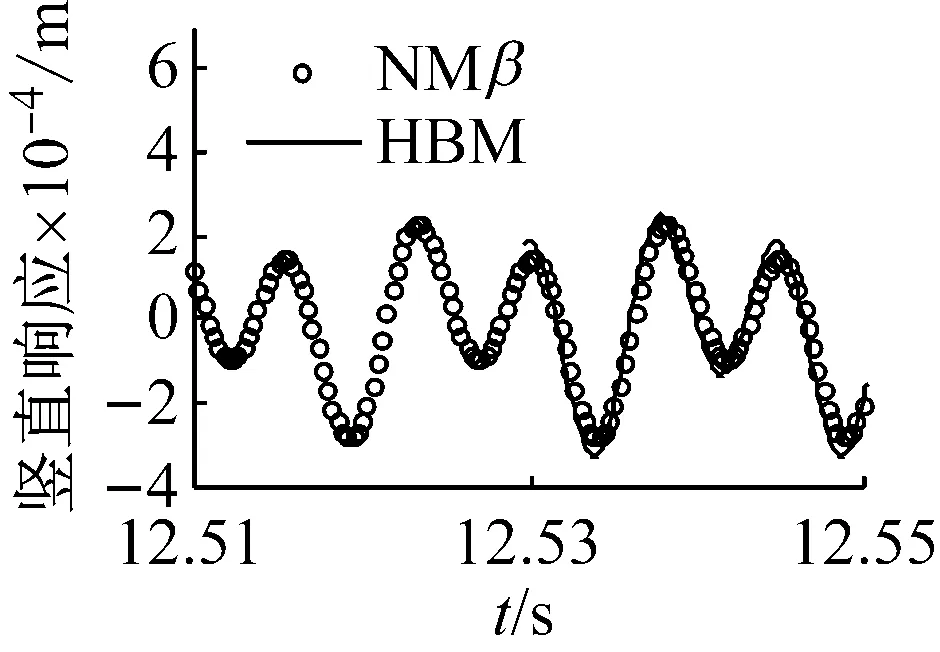
(b) 豎直方向時間歷程

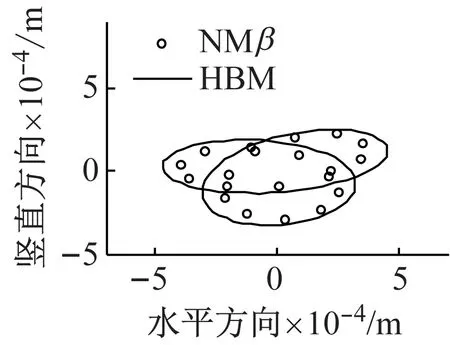
(c) 軸心軌跡圖

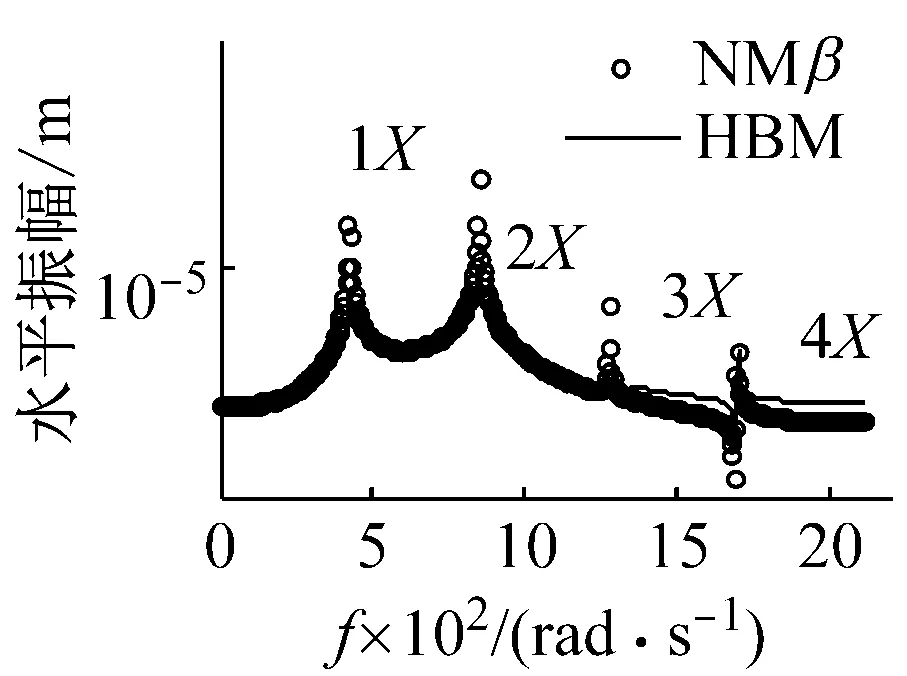
(d) 水平方向頻譜圖

5 結 論

本文針對某航空發動機高壓轉子-空心軸裂紋系統，研究了空心軸呼吸裂紋轉子系統的動力學特性，建立了含有橫向弓形呼吸裂紋的單跨雙盤有限元模型，推導了空心Timoshenko梁-軸裂紋轉子系統的剛度矩陣，基于有限元法建立了系統的運動方程，并用諧波平衡法對方程進行求解，分析了系統的非線性響應等動力學特性，最后用Newmark-β方法進行了數值驗證，結論如下：

(1) 分析了裂紋位置和裂紋深度對系統響應的影響，結果表明，裂紋導致系統正反向臨界轉速和1/n(n=2，3，4)臨界轉速附近出現共振峰值；同時裂紋“削弱”了系統剛度，一階臨界轉速略有降低；位于支承端附近的淺裂紋對系統的影響相對較小，而位于跨中的深裂紋對系統的影響相對較大。

(2) 計算了系統在升速過程中的三維頻譜圖，結果表明二倍頻、三倍頻、四倍頻成分明顯；同時在1/n(n=2，3，4)倍臨界轉速附近的非線性振動響應表明，系統會發生超諧共振現象，頻率成分以對應共振超諧波階數的倍頻為主，軸心軌跡是疊加的橢圓。

(3) 本文建立的空心軸裂紋模型適用于空心軸裂紋轉子系統的非線性動力學研究，為航空發動機裂紋轉子系統非線性振動的理論分析與數值模擬提供了理論依據。

[1] 陳予恕, 張華彪. 航空發動機整機動力學研究進展與展望[J]. 航空學報, 2011, 32(8): 1371-1391.

CHEN Yushu, ZHANG Huabiao. Review and prospect on the research of dynamics of the aero-engine system[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1371-1391.

[2] GASCH R. Dynamic behavior of a simple rotor with a cross sectional crack[M]. London: Vibrations in Rotating Machinery, 1976: 123-128.

[3] MAYES I W, DAVIES W G R. Analysis of the response of a multi-rotor-bearing system containing a transverse crack in a rotor[J]. ASME Journal of Vibration, Acoustics, Stress, and Reliability, 1984, 106(1): 139-145.

[4] 林言麗, 褚福磊. 裂紋轉子的剛度模型[J]. 機械工程學報, 2008, 1(1):114-120.

LIN Yanli, CHU Fulei. Stiffness models for the cracked shaft of the rotor system[J]. Journal of Mechanical Engineering, 2008, 1(1):114-120.

[5] 王仲生, 姜洪開, 徐一艷. 發動機轉子系統早期故障智能診斷[J]. 航空學報, 2009, 30(2):242-246.

WANG Zhongsheng, JIANG Hongkai, XU Yiyan. Early fault intelligent diagnosis of aero-engine rotor systems[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2):242-246.

[6] 王國彪, 何正嘉, 陳雪峰,等. 機械故障診斷基礎研究“何去何從”[J]. 機械工程學報, 2013, 49(1):63-72.

WANG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Basic research on machinery fault diagnosis—What is the prescription[J]. Journal of Mechanical Engineering, 2013, 49(1):63-72.

[7] 程禮, 何正嘉, 李寧, 等. 裂紋非線性呼吸行為對轉子臨界轉速的影響[J]. 振動與沖擊, 2010, 29(4): 44-47.

CHENG Li, HE Zhengjia, LI Ning, et al. Influence of crack nonlinear breathing behavior on critical speed of rotor[J]. Journal of Vibration & Shock, 2010, 29(4):44-47.

[8] AL-SHUDEIFAT M A, BUTCHER E A. New breathing functions for the transverse breathing crack of the cracked rotor system: approach for critical and subcritical harmonic analysis[J]. Journal of Sound and Vibration, 2011, 330(3): 526-544.

[9] HE Erming, REN Xingmin, QIN Weiyang. Chaotic response of cracked rotor supported on squeeze film damper and the routes to chaos[J]. Chinese Journal of Aeronautics, 2002, 15(3):145-149.

[10] 萬方義, 許慶余, 華軍. 非線性油膜支承裂紋轉子振動特性分析[J]. 航空學報, 2002, 23(3):237-240.

WAN Fangyi, XU Qingyu, HUA Jun. Analysis on the vibration characteristics of cracked rotor with nonlinear oil film bearing[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(3):237-240.

[11] HAN Qinkai, CHU Fulei. Parametric instability of a rotor-bearing system with two breathing transverse cracks[J]. European Journal of Mechanics-A/Solids, 2012, 36(36): 180-190.

[12] HOU Lei, CHEN Yushu. Super-harmonic responses analysis for a cracked rotor system considering inertial excitation[J]. Science China Technological Sciences, 2015, 58(11): 1924-1934.

[13] HOU Lei, CHEN Yushu, LU Zhenyong, et al. Bifurcation analysis for 2∶1 and 3∶1 super-harmonic resonances of an aircraft cracked rotor system due to maneuver load[J]. Nonlinear Dynamics, 2015, 81(1/2):531-547.

[14] 侯磊, 陳予恕, 李忠剛. 一類兩自由度參激系統在常數激勵下的響應研究[J]. 物理學報, 2014, 63(13):246-253.

HOU Lei, CHEN Yushu, LI Zhonggang, et al. Constant-excitation caused response in a class of parametrically excited systems with two degrees of freedom[J]. Acta Physica Sinica, 2014, 63(13):246-253.

[15] 于海, 陳予恕, 曹慶杰. 多自由度裂紋轉子系統非線性動力學特性分析[J]. 振動與沖擊, 2014, 33(7): 92-98.

YU Hai, CHEN Yushu, CAO Qingjie. Bifurcation analysis for a nonlinear cracked multi-degree-of-freedom rotor system[J]. Journal of Vibration and Shock, 2014, 33(7): 92-98.

[16] AL-SHUDEIFAT M A, BUTCHER E A, STERN C R. General harmonic balance solution of a cracked rotor-bearing-disk system for harmonic and sub-harmonic analysis: analytical and experimental approach[J]. International Journal of Engineering Science, 2010, 48(10): 921-935.

[17] AL-SHUDEIFAT M A. On the finite element modeling of the asymmetric cracked rotor[J]. Journal of Sound and Vibration, 2013, 332(11): 2795-2807.

[18] SINOU J J, LEES A. The influence of cracks in rotating shafts[J]. Journal of Sound and Vibration, 2005, 285(4): 1015-1037.

[19] SINOU J J, LEES A. A non-linear study of a cracked rotor[J]. European Journal of Mechanics-A/Solids, 2007, 26(1): 152-170.

[20] 路振勇, 陳予恕, 侯磊,等. 常開空心軸裂紋轉子系統的動力學特性[J]. 航空動力學報, 2015, 30(2): 422-430.

LU Zhenyong, CHEN Yushu, HOU Lei, et al. Dynamic characteristics of a open crack in hollow shaft rotor system[J]. Journal of Aerospace Power, 2015, 30(2):422-430.

[21] LU Zhenyong, HOU Lei, CHEN Yushu, et al. Nonlinear response analysis for a dual-rotor system with a breathing transverse crack in the hollow shaft[J]. Nonlinear Dynamics, 2016, 83(1/2):169-185.

[22] 航空發動機設計手冊總編委會. 航空發動機設計手冊(第19分冊)轉子動力學及整機振動[M]. 北京：航空工業出版社，2000:57-130.

[23] 鐘一諤, 何衍宗, 王正, 等. 轉子動力學[M]. 北京: 清華大學出版社, 1987:176-192.

[24] 陳予恕. 非線性振動[M]. 北京: 高等教育出版社, 2002:53-57.