移動簡諧荷載作用下Kerr地基梁的穩態響應研究

黃 強， 黃宏偉， 張冬梅， 黃 栩

(1. 同濟大學 土木工程學院地下建筑與工程系， 上海 200092； 2. 同濟大學 巖土及地下工程教育部重點實驗室， 上海 200092;3. 中鐵二院華東勘察設計有限責任公司， 杭州 310006)

地表列車運行引起軌道結構響應一直是鐵路工程師研究的熱點[1]。隨著現代鐵路運行速度越來越高，列車的運行速度有可能超過下臥地層的瑞利波速而引起土層振動的劇烈增加，此時列車速度已經超過了地基-梁系統的臨界速度。Krylov[2]預測當列車速度超過下臥土層的瑞利波波速時，將導致地基和軌道的急劇增加，類似于飛機突破音障而產生的音爆現象。地表軌道位移的劇烈增加勢必影響到列車運行安全，因此，評估列車運行引起的軌道響應就顯得十分必要。

分析地表列車移動引起的地基-梁響應最簡單常見的做法是將之視為地基上無限長梁的穩態響應問題。迄今為止，對于地基梁的振動響應研究已是相當廣泛。概括而言，可以歸納為三個方面：一是考慮地基模型不同，常見有單參數的Winkler地基[3]、兩參數的Pasternak地基[4]、Vlasov地基[5]等，根據地基阻尼考慮與否又可相應地分為黏彈性地基和彈性地基兩種情況；二是考慮梁類型不同，一般為歐拉梁(Euler-Bernoulli梁)和鐵木辛柯梁(Timoshenko梁)兩種；三是考慮荷載形式不同，有移動常載、簡諧荷載以及分布線荷載等多種形式。例如，Kenney[6]研究了移動常載作用下Winkler彈性地基梁的穩態響應，地基梁視作Euler-Bernoulli梁。結果表明，當荷載移動速度等于無阻尼條件下的臨界速度時，地基梁將發生共振，其撓度增加到無限大；Fryba[7]利用Fourier變換得到了移動常載下Winkler地基梁的撓度響應解答，詳細分析了欠阻尼、臨界阻尼和過阻尼三種情況下撓度解的形式；Sun[8]利用格林函數和二重Fourier變換方法得到了移動簡諧均布線荷載作用下黏彈性地基梁的位移響應封閉解，分析了不同地基阻尼和荷載頻率下解的形式，并對解析解進行了驗證；Kargarnovin等采用Fourier變換方法和圍道積分方法得到了任意分布形式移動簡諧荷載作用下Pasternak地基梁的穩態響應解析解答，梁被視為Timoshenko梁，得到了梁的撓度、彎矩以及剪力響應曲線，分析了荷載速度和頻率的影響；Mallik等[9]分析了Pasternak地基上歐拉梁的穩態響應，并利用Fourier變換求解方法對解析解數學表達形式進行了驗證，比較了欠阻尼和過阻尼情況下位移響應的解答形式；Chen等[10]提出動力剛度矩陣求解方法，分析了移動簡諧荷載作用下黏彈性地基上Timoshenko梁的動力響應，認為地基梁的臨界速度和共振頻率可以通過動力剛度矩陣予以確定；此外，Zhen等[11]研究了移動簡諧荷載作用下彈性地基上Timoshenko梁的臨界速度問題。

從已有的研究來看，目前的研究主要存在兩個不足。首先，高級的地基模型較少采用。如三參數Kerr地基模型[12]；二是對于不同地基模型下的動力響應計算結果缺少對比分析，各模型的適用效果缺少進一步的驗證。黃栩[13]以軟土隧道上部基坑開挖引起的隧道隆起為例，比較了Kerr地基、Pasternak地基和Winkler地基模型的解析計算結果與有限元計算結果，證明Kerr地基模型與有限元分析結果為最接近，而Winkler地基梁的解析結果誤差最大。但是對于動力荷載作用的情況，目前對比研究鮮見報道。

分析地基梁穩態響應，地基模型選擇是最關鍵的因素。高級模型雖然計算過程可能更為復雜，但是其計算精度也更高，在實際應用中仍有重要的價值。目前的研究對于探討高級地基模型響應的還較少，因此，本文利用Kerr地基模型，分析其在移動荷載作用下的穩態響應特征，最后建立地基-梁有限元模型，比較不同地基梁模型的解析結果和有限元結果差異，指出Kerr地基模型的優勢。

1 Kerr地基梁穩態響應解答

Kerr地基梁模型如圖1所示。假設梁為歐拉梁，Kerr地基模型由上、下兩層彈簧和中間剪切層組成，模型參數為地基壓縮系數k1、k2和剪切系數G，剪切層可以起到協調彈簧變形的效果。

圖1 Kerr地基梁模型

Kerr地基梁的振動方程為

(1)

式中：y1，y2分別為地基梁和剪切層的撓度，m；E1I1為梁的抗彎剛度，Nm2；m1為每單位長度梁質量，kg/m；k1、k2分別上、下層地基壓縮系數，N/m3；c2為地基阻尼，Ns/m3；G為剪切剛度系數，N/m；b為梁的寬度，假設為1 m；p0為荷載幅值，N；w0為荷載圓頻率，rad/s；v為列車移動速度，m/s。對式(1)進行雙重Fourier積分變換，將時域-空間域的振動方程轉換成波數域-頻域內的形式。雙重Fourier變換及其逆變換形式如下

(2)

經過Fourier變換后的Kerr地基梁振動方程表達為

(3)

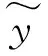
(4)

式(4)中f1(ξ,w)、f2(ξ,w)、f3(ξ,w)表達式如下

f1(ξ,w)=

(5a)

f2(ξ,w)=-(k1+k2+ic2w+Gξ2)

(5b)

f3=k1

(5c)

對式(4)進行傅里葉逆變換，并采用圍道積分方法即可得到移動簡諧荷載作用下Kerr地基梁撓度穩態響應解析表達式，如式(6)所示

(6)

式中:ξ1，ξ2，ξ3為ξ虛軸正半區域根和ξ實軸負半軸上的根；ξ4，ξ5，ξ6為ξ虛軸負半區域根和ξ實軸正半軸上的根。ξ1-ξ6為f1(ξ,w=w0-ξv)=0的6個復數根。在實際解答中，ξ1，ξ2,…,ξ6可能具有三種不同的根形式：只有實數部分或復數部分，或實數和復數部分都有。

2 Kerr地基梁穩態響應計算結果

各地基模型的地基參數一般可以通過簡化彈性空間法換算求得[14]。Kerr地基模型的換算公式為

(7)

式中:Es、Gs分別為地基的彈性模量和剪切模量，Pa；H為土層厚度，m。本文算例中假設Es=50 MPa，泊松比v=0.3，H=15 m，可得Kerr地基參數為k1=13.33 MPa/m，k2=4.44 MPa/m，G0=128.20 MN/m。假設鋼軌梁為UIC60鋼軌，有E1I1=6.12×106N/m2，m1=60.34 kg/m；假設p0=80 kN。

2.1 地基梁頻散曲線

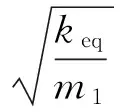
在式(6)中，必須滿足w=w0-ξv，于是假設有不同w0下的w=w0-ξv直線，如圖2中所示。隨著列車速度v增大或w0增大，w=w0-ξv直線逐漸向頻散曲線靠近，一旦w=w0-ξv直線與頻散曲線相交，即有點(ξ,w)處于頻散曲線上，此時f1(ξ,w)=0成立，地基梁就會發生共振，在無地基阻尼時，梁的振動撓度會趨于無窮大，有地基阻尼時，地基梁撓度則會劇增至一較大值[15]。我們把直線w=w0-ξv與頻散曲線相切時的列車速度稱為臨界速度。可以看出，地基梁的臨界速度受荷載頻率的影響，荷載頻率增大，Kerr地基梁臨界速度會變小，如圖3所示。當荷載為移動常載時，計算得到列車臨界速度為537 m/s，荷載頻率為20 Hz時，臨界速度降為424 m/s。

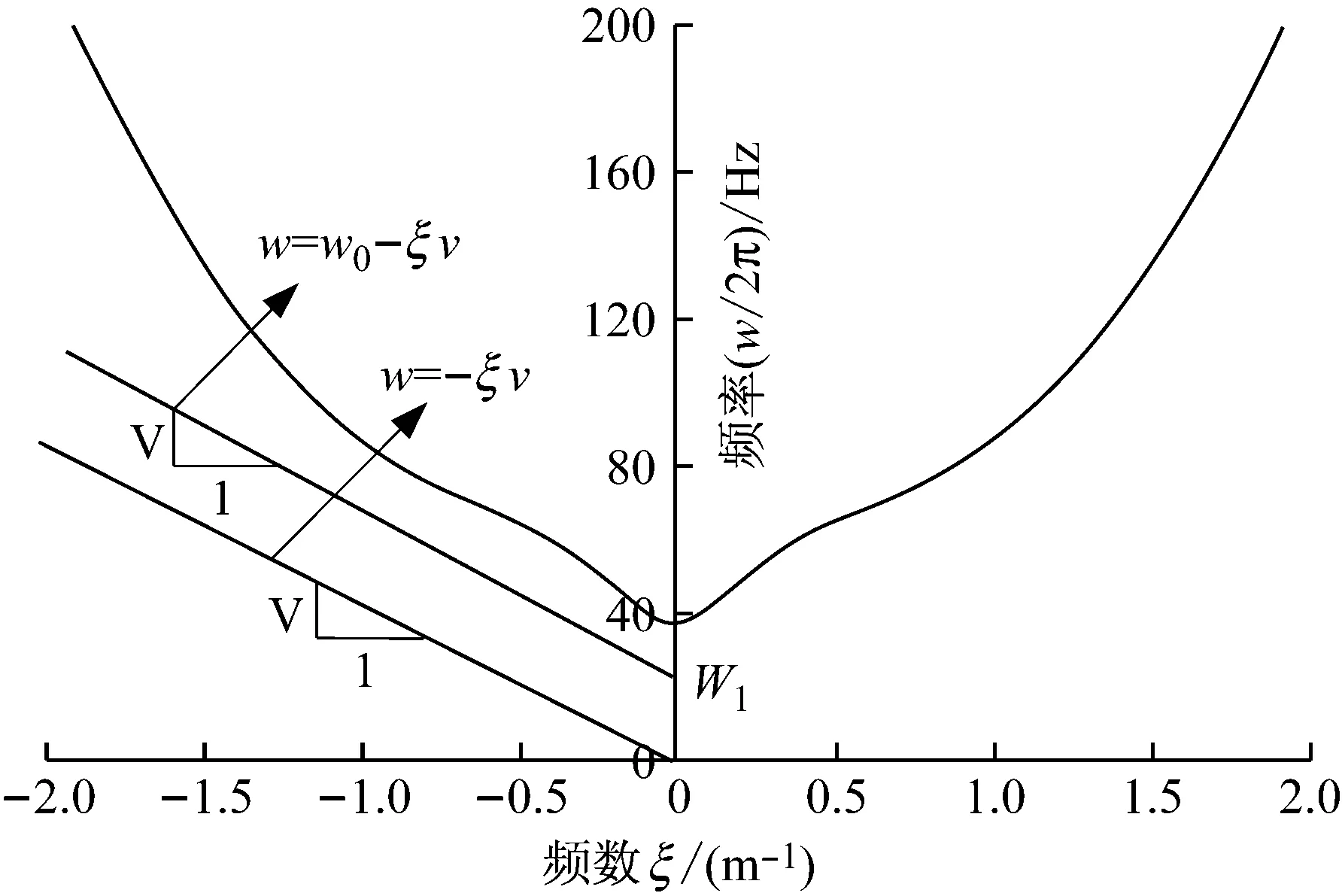
圖2 Kerr地基梁頻散曲線

圖3 不同荷載頻率下Kerr地基梁臨界速度

2.2 不考慮地基阻尼時Kerr地基梁響應

當不考慮地基阻尼的存在時(c2=0)，Kerr地基梁為彈性地基梁。通過計算，靜載作用下梁的撓度為4.03 mm。

2.2.1 列車運行速度的影響

圖3可以看出，不同的荷載頻率下地基梁的撓度曲線隨列車速度的變化規律相似。在列車速度未達到臨界速度之前，地基梁撓度隨著列車速度有輕微增加的趨勢，當列車運行速度接近列車臨界速度時地基梁撓度會急劇增大，而當列車速度超過臨界速度后，荷載作用點的撓度急劇下降并隨著速度增加逐漸減小。然而，臨界速度前后地基梁的撓度響應是大為不同的。以20 Hz下的移動簡諧荷載為例，不同速度下的撓度曲線如圖4所示。當列車速度遠小于臨界速度時，地基梁撓度曲線左右對稱；當列車速度接近臨界速度時，最大撓度值快速增加，同時地基梁兩側會出現撓度波動現象；當列車速度超越臨界速度后，地基梁撓度曲線變得左右不對稱，荷載后側方向梁的撓度出現明顯起伏，存在多個峰值點，此時梁的最大撓度會在荷載移動向前方出現。

圖4 列車速度對Kerr地基梁撓度的影響(f=20 Hz)

2.2.2 荷載頻率的影響

荷載頻率對地基梁撓度的影響如圖5和圖6所示。圖5表明當列車速度小于臨界速度時，地基梁的共振頻率等于自振頻率，地基梁撓度隨荷載頻率變化曲線幾乎一致；圖6表明在共振頻率前后地基梁的撓度響應是不同的。未達到共振頻率前，梁撓度先隨著荷載頻率增加逐漸增加，當荷載頻率達到地基-梁自振頻率時，地基梁發生共振，荷載頻率繼續增大時，荷載作用點處梁撓度反而減少，左右側撓度響應不一致，與前述列車速度的影響有相似之處。造成這樣的原因是，當荷載頻率較小時，w=w0-ξv直線與頻散曲線沒有交點，故地基梁不會發生共振，當荷載頻率超過了自振頻率時，w=w0-ξv直線此時與頻散曲線有兩個交點，導致撓度曲線左右側都會出現撓度峰值點，此時左右側的撓度響應并不一致，出現了起伏。

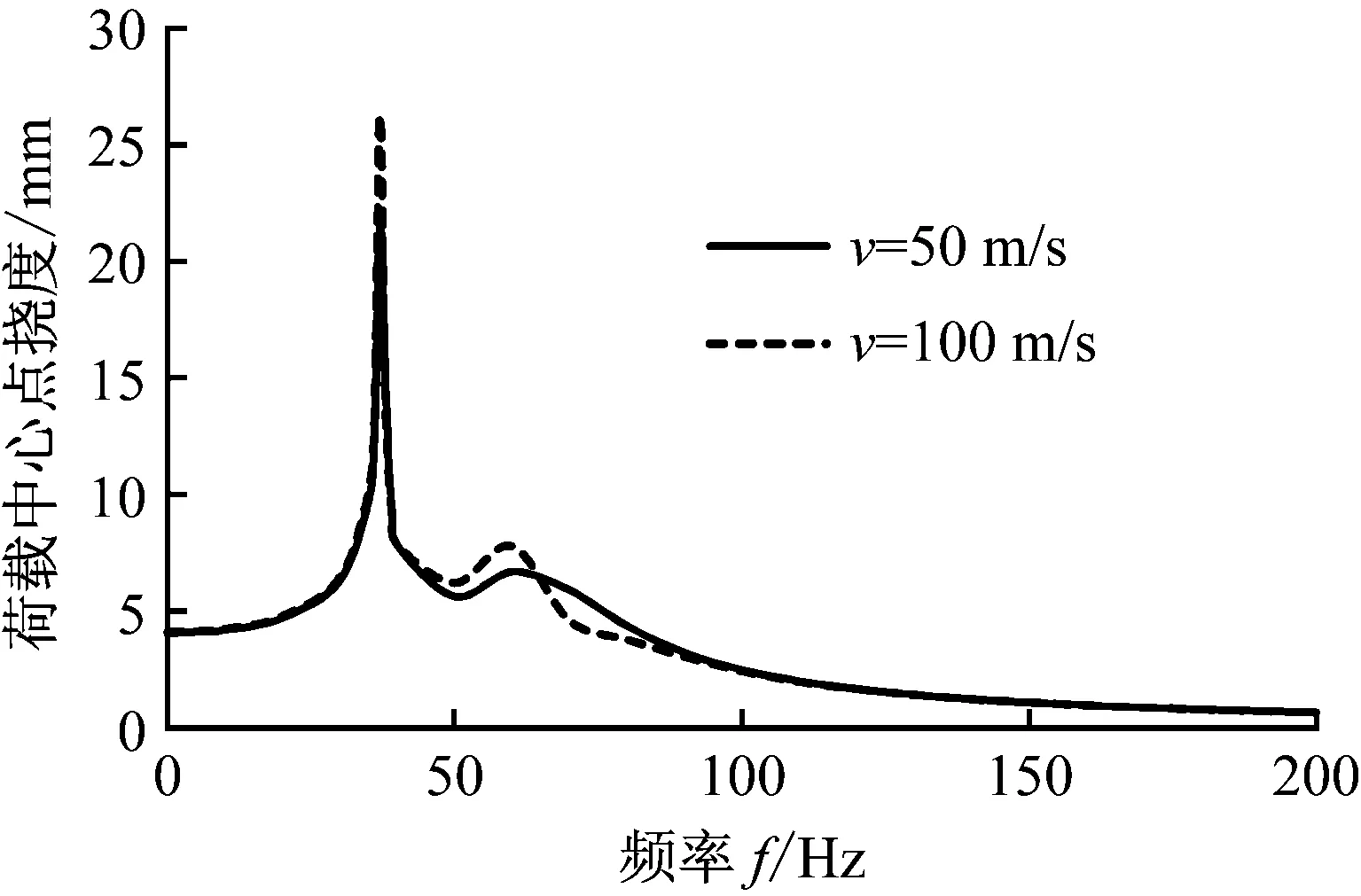
圖5 荷載頻率對Kerr地基梁撓度影響(低于臨界速度)

圖6 不同荷載頻率下Kerr地基梁撓度曲線(v=50 m/s)

2.2.3 地基壓縮系數和剪切系數的影響

圖7和8給出了不同地基壓縮系數和剪切系數下Kerr地基梁撓度曲線。圖7可以看出，地基梁撓度受Kerr地基梁上下層地基壓縮系數比值影響較大。隨著k1/k2比值增大(這里k2一定，k1增大)，梁的撓度會快速減少，但最終地基梁撓度會趨于穩定。這是因為隨著k1/k2越大，地基彈簧的等效壓縮系數越來越近k2。Avramidis等[16]認為為了獲得較精確的計算結果，采用Kerr地基模型時可將上層彈簧壓縮系數k1的取值調整為k1=nk2，其中n為調整系數。黃栩在其研究中認為n=7時地基梁的撓度和彎矩計算值與有限元結果最為接近。

圖8為地基剪切系數對地基梁撓度的影響，可以發現隨著G增大，地基梁的撓度有所減少，但改變幅度在變少，表明一味增大剪切系數G并不能有效減少地基梁的撓度，G0已滿足增強地基彈簧協調變形要求。圖7和8表明，Kerr地基參數中地基壓縮系數比值是影響Kerr地基梁計算精度重要的因素，取k1=7k2，G=G0可滿足計算精度的要求。

圖7 k1/k2比值對Kerr地基梁撓度影響(k2=4.44×106N/m3,v=50 m/s)

Fig.7 Influence ofk1/k2on the deflection of Kerr foundation beam(k2=4.44×106N/m3,v=50 m/s)

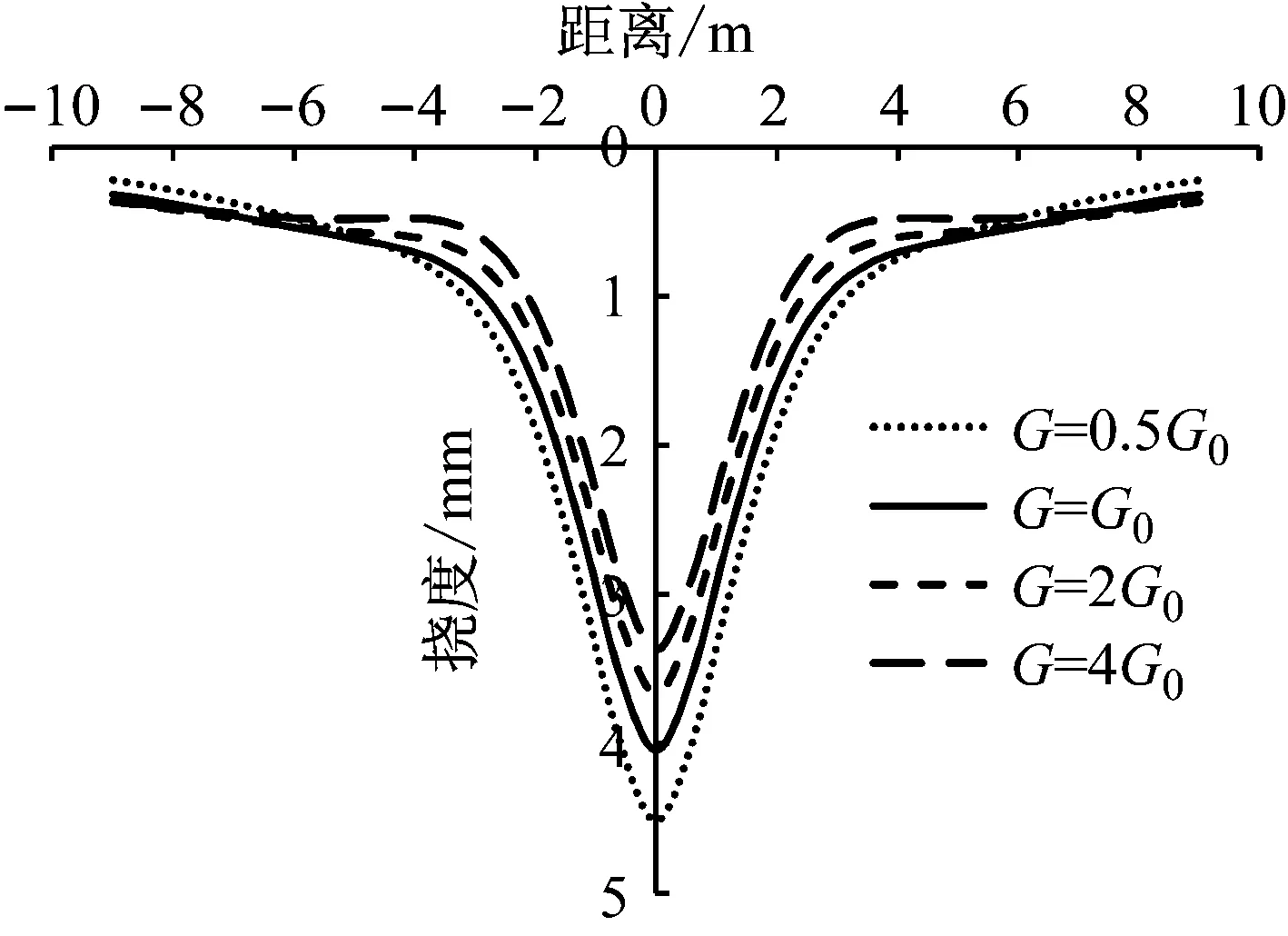
圖8 剪切系數G對Kerr地基梁撓度影響(G0=

Fig.8 Influence of shear coefficientGon the deflection of Kerr foundation beam(G0=1.282×108N/m,v=50 m/s)

2.3 考慮地基阻尼下Kerr地基梁穩態響應

地基梁發生共振與列車速度和荷載頻率有關，因此，可以分析地基阻尼對臨界速度和共振頻率的影響。地基阻尼對臨界速度的影響如圖9所示，地基阻尼增加會使得臨界速度有輕微的增加，但阻尼繼續增大，臨界速度幾乎不增加。其次，當荷載頻率小于共振頻率時，發現阻尼存在會使得地基梁撓度有所減少。在列車速度小于臨界速度時，有無阻尼下的地基梁撓度響應曲線相似，而列車速度大于臨界速度后，兩者的撓度響應會有明顯的不同，如圖10所示，表明地基阻尼對超過臨界速度下的地基梁撓度響應有重要影響。

圖9 地基阻尼對Kerr地基梁臨界速度影響(f=20 Hz)

圖10 有無地基阻尼下列車速度對Kerr地基梁撓度的影響(f=20 Hz)

Fig.10 Influence of train speed on the deflection of Kerr foundation beam under the existence or nonexistence of damping(f=20 Hz)

圖11可以看出，當列車速度小于臨界速度時，地基阻尼增加會使得地基梁的共振頻率有所增加，從37 Hz增加到72 Hz，但地基阻尼繼續增加時，共振頻率幾乎不變，但發生共振時地基梁撓度最大值會繼續增大。比較有無地基阻尼時不同頻率下的Kerr地基梁撓度曲線，發現兩者基本一致，但是荷載頻率小于共振頻率時，有阻尼時的地基梁最大撓度小于無阻尼的情況，而荷載頻率大于共振頻率時，則是有阻尼下的地基梁撓度稍大，說明地基阻尼對超過共振頻率下的地基梁撓度響應影響不大。如圖12所示。

圖11 地基阻尼對地基梁共振頻率影響(v=50 m/s)

3 Kerr地基梁模型驗證以及地基模型比較

為了驗證Kerr地基梁解答的合理性，本文將Kerr地基梁的計算結果與Pasternak地基梁和Winkler地基梁進行對比。Pasternak地基梁模型如圖13所示，在移動簡諧荷載作用下的振動響應方程為

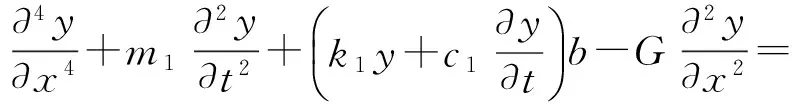
p0eiw0tδ(x-vt)

(8)

圖12 有無地基阻尼下頻率對地基梁撓度的影響(v=50 m/s)

Fig.12 Influence of frequency on the deflection of Kerr foundation beam in the case of the existence or nonexistence of damping(v=50 m/s)

可以看出，當Pasternak地基剪切系數G=0時，Pasternak地基就退化為Winkler地基。因而可以將Pasternak地基看作Winkler模型的改進，Kerr地基中G=0時也可退化為等效地基壓縮系數下的Winkler地基，所以也是一種改進。

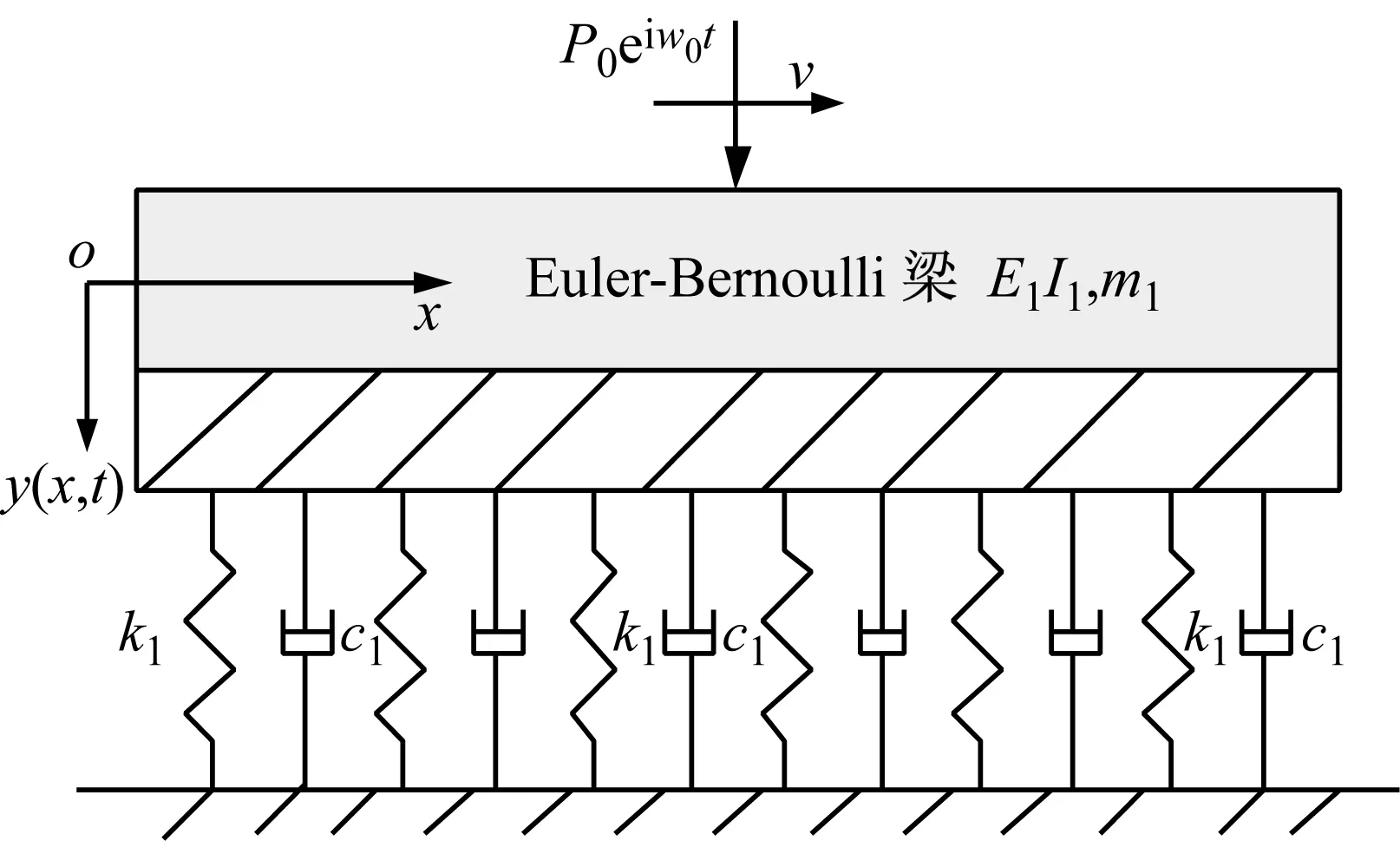
圖13 Pasternak地基梁模型

為了比較不同地基梁模型的計算精度，建立二維有限元模型予以驗證，如圖14所示。梁為UIC60鋼梁，參數如前所述，荷載頻率為20 Hz，p0=80 kN。

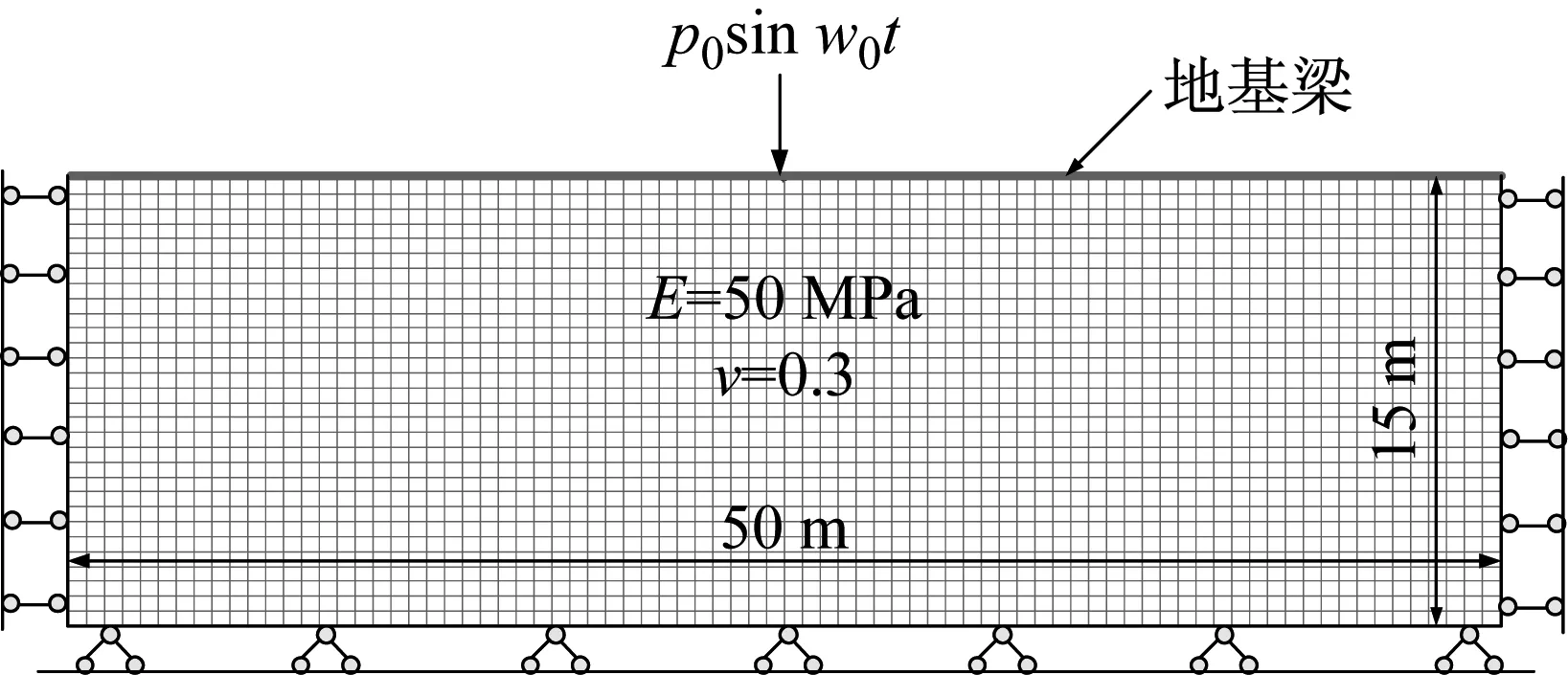
圖14 二維有限元模型

根據簡化彈性空間法，可以得到Pasternak地基模型和Winkler地基模型參數如下

(9)

式中:kp，Gp分別是Pasternak地基壓縮系數和剪切系數；kw為Winkler 地基壓縮系數。Kerr地基模型參數取k1=7k2，其他參數仍依據式(7)確定。

比較靜載和簡諧荷載作用下地基梁模型解析計算和有限元計算結果，如圖15和16、17所示。圖15可以看出，在靜力荷載作用下，有限元計算結果與Kerr地基梁計算結果最為接近，且撓度曲線形態也相似，Pasternak地基梁在荷載作用點處撓度會偏小，Winkler地基梁結果與有限元結果差異最大，且撓度曲線形態與有限元結果也相差較大。由此看出，在靜載作用下，Kerr地基梁的計算精度最高，Pasternak次之，Winkler地基模型誤差較大。

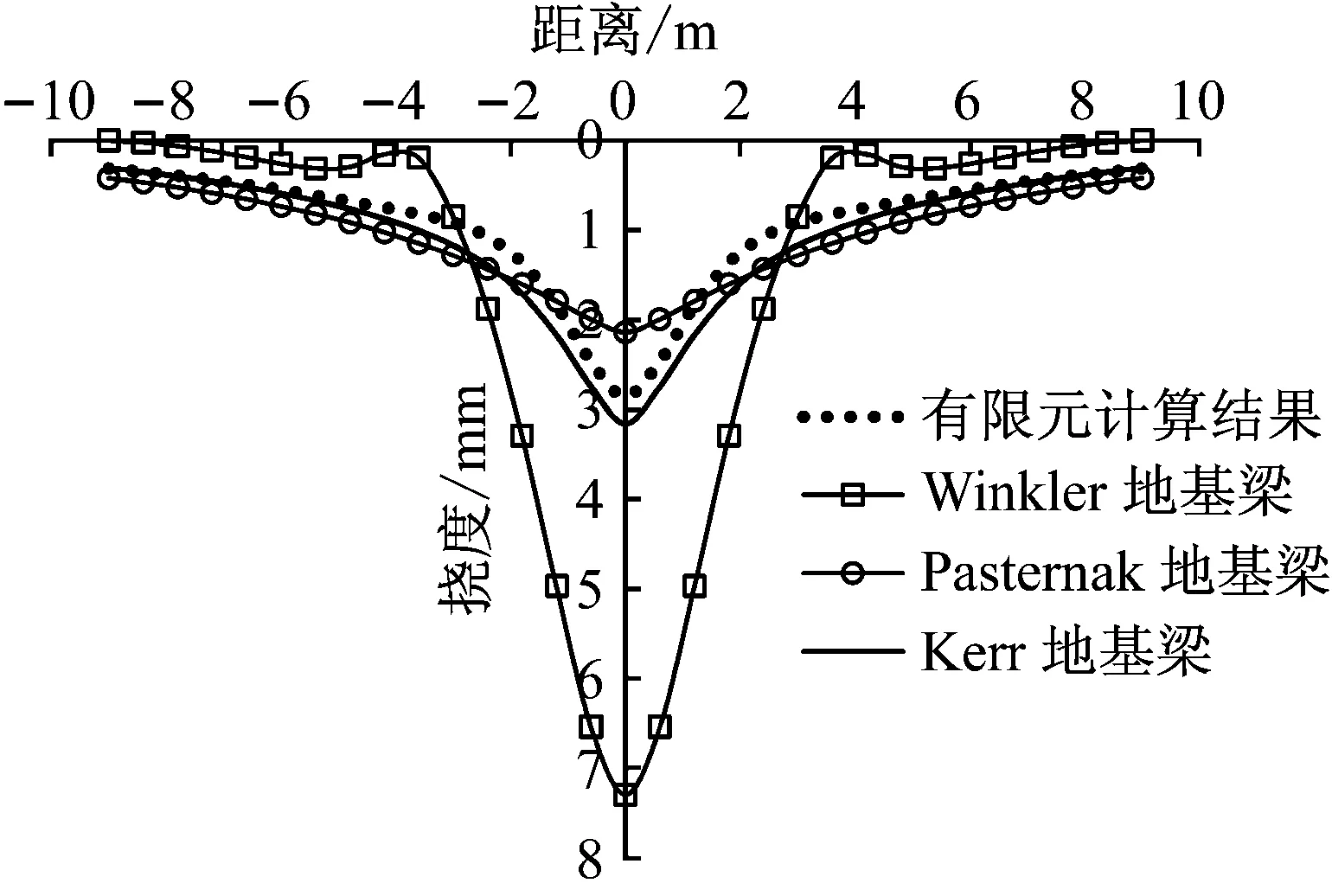
圖15 靜力荷載作用下各地基梁計算結果比較

圖16 撓度時程曲線對比(x=0 m)

圖17 撓度時程曲線對比(x=4.8 m)

圖16、17比較了簡諧荷載作用下有限元計算結果和解析計算結果。可以看出，動力荷載作用下，有限元結果與解析結果差異與位置有關。在荷載作用點處，有限元計算的位移時程響應與解析計算基本類似。從撓度幅值看，Kerr地基梁計算結果和有限元結果差異最小，Pasternak次之，Winkler地基梁的撓度則偏大較多。在遠離荷載位置處，有限元結果和解析結果時程響應曲線相差很大，很難分辨出哪種地基梁模型更為合理。造成如此差異的原因是各地基梁模型中地基被簡化為無質量的彈簧和剪切層，而有限元模型中地基是實體單元，地基模型具有質量和慣性，因而在外部動荷載作用下，有限元中梁的撓度響應不可能像各地基梁模型那樣與簡諧荷載時程曲線完全一致。采用地基梁模型計算結果是一種簡單的近似手段。

4 結 論

本文分析移動簡諧荷載作用下了Kerr地基梁的穩態響應特征，并同其他的地基梁模型比較，得到以下幾個結論：

(1) 利用頻散曲線可以確定地基梁的自振頻率以及列車臨界速度。頻率-波數直線與頻散曲線是否存在交點是判定地基梁響應在共振前還是共振后階段的判定，移動荷載作用下地基梁發生共振與臨界速度和荷載頻率都有關，Kerr地基梁撓度曲線在臨界速度或共振頻率前后有明顯的不同。

(2) Kerr地基梁撓度受上下層地基壓縮系數比值和地基剪切系數影響，當地基系數比值和剪切系數不斷增加時，地基梁撓度會趨于穩定，取k1=7k2，G=G0可滿足計算精度的要求。

(3) 地基阻尼增加會使得地基梁的共振頻率和臨界速度有所增加，但很快達到穩定。地基阻尼的存在會一定程度上減少地基梁的撓度響應。

(4) 靜載作用下，Kerr地基梁的計算精度最高，Pasternak模型次之，Winkler模型計算精度最差，在動力荷載作用下，地基梁的撓度時程響應解析計算結果與有限元計算結果差異較大，僅在荷載作用點處兩者的撓度時程響應較為接近。

[1] KARGARNOVIND M H, YOUNESIAN D. Dynamics of Timoshenko beams on Pasternak foundation under moving load[J]. Mechanics Research Communications, 2004, 31: 713-723.

[2] KRYLOV V V. Generation of ground vibration by superfast trains[J]. Applied Mechanics,1995,44:149-164.

[3] WINKLER E. Die lehre von elastizit?t und festigkeit(The theory on elasticity and fixity)[M]. Prague: Dominicus, 1867.

[4] PASTERNAK P L. Fundamentals of a new method of analyzing structures on an elastic foundation by means of two foundation moduli[M].Moscow: Gosudarstvennoe Izdatelstro Liberaturipo Stroitelstvui Arkhitekture, 1954.

[5] VLAZOV V Z, LEOTIEV U N. Beams, plates and shells on elastic foundations[M].Jerusalem: Israel Program for Scientific Translations, 1966.

[6] KENNEY T. Steady-state vibrations of beam on elastic foundation for moving load[J]. Journal of Applied Mechanics, Transactions ASME,1954,21:359-364.

[8] SUN L. A closed-form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic loads[J]. Journal of Sound and Vibration,2001,242(4):619-627.

[9] MALLIK A K, CHANDRA S, SINGH A B. Steady-state response of an elastically supported infinite beam to a moving load[J]. Journal of Sound and Vibration,2006,291:1148-1169.

[10] CHEN Y H, HUANG Y H, SHIH C T. Response of an infinite Timoshenko beam on a viscoelastic foundation to a harmonic moving load[J]. Journal of Sound and Vibration,2001,241(5):809-824.

[11] ZHEN B, LUO W, XU J. Analysis of critical velocities for an infinite Timoshenko beam resting on an elastic foundation subjected to a harmonic moving load[J]. Shock and Vibration,2014(2):1-9.

[12] KERR A D. Elastic and viscoelastic foundation models[J]. Journal of Applied Mechanics, Transactions ASME,1964:31(3):491-498.

[13] 黃栩. 軟土基坑開挖對下臥已建隧道的影響研究[D]. 上海：同濟大學，2012.

[14] HORVATH J S. New subgrade model applied to mat foundations[J]. Journal of Geotechnical Engineering, 1983, 109(12): 1567-1587.

[15] HUSSEIN M F M, HUNT H E M. Modelling of floating-slab tracks with continuous slabs under oscillating loads[J]. Journal of Sound and Vibration,2006,297:37-54.

[16] AVRAMIDIS I E, MORFIDIS K. Bending of beams on three-parameter elastic foundation[J]. International Journal of Solids and Structures,2006,43:357-375.