含鉸可展桁架結構非線性模型修正方法研究

宋正華， 姜 東， 曹芝腑， 韓曉林， 費慶國

(1. 東南大學 工程力學系， 南京 210096； 2. 南京林業(yè)大學 機械電子工程學院， 南京 210037)

在空間站建設、深空探測等航天任務中，大型桁架式可展結構得到了廣泛的應用，例如衛(wèi)星天線的支撐結構、柔性太陽能帆板的展開支撐臂等結構[1-2]。可展結構各部件之間通過鉸鏈來連接，例如，美國NASA用于航天飛機對地進行高分辨率觀測的ADAM支撐臂全部展開長60 m，由87個桁架單元構成，含有696個鉸鏈[3]。鉸鏈中存在間隙，在外載荷作用下會發(fā)生摩擦和碰撞等非線性現(xiàn)象，對結構的工作精度和抗干擾能力產(chǎn)生不利影響。因此，鉸鏈對結構動力學特性的影響不可忽視，需要對鉸鏈的力學特性展開研究，為設計提供可靠的評價和參考。國內(nèi)外學者圍繞含鉸結構開展了相關的研究：Ferney等[4-5]基于力狀態(tài)映射方法進行鉸鏈的實驗研究，Tomihiko等[6-7]通過實驗建立了鉸鏈的非線性剛度和阻尼模型；Webster等[8-9]基于描述函數(shù)法、殘余力法和諧波展開法等進行非線性力描述，利用有限單元法進行了無約束含鉸鏈結構的動力學分析；黃鐵球等[10]對鉸鏈的物理模型進行分析，得出了鉸間相互作用力的關系，并通過建立有限單元模型得到了桁架結構的非線性動力學模型；陳鹿民等[11]設計了一個動力型桁架式可展結構，并對其進行了動力學實驗研究；尉立肖等[12]研究圓柱副間隙結構的間隙接觸碰撞模式，對曲柄結構進行了動力學仿真；閻紹澤等[13]研究碰撞及摩擦力對可展結構動力學性能的影響。然而，對于非線性結構的反問題的研究還較少，由于動力學反問題的研究是建立準確的結構有限元模型和結構優(yōu)化設計的重要環(huán)節(jié)，所以對非線性結構的反問題的研究也相當重要。

目前，有限元模型修正方法基本都是建立在線性結構基礎之上[14]，但是實際工程當中，振動結構都是非線性的，線性只是在一定條件下的近似。當非線性比較明顯時，一般的線性模型修正方法不再適用，所以對非線性結構模型修正方法的研究也相當重要。費慶國等[15]提出了基于神經(jīng)網(wǎng)絡的非線性結構的修正方法，并將此方法應用到了非線性梁結構的有限元模型修正；Tang等[16]提出了主要針對可積非線性系統(tǒng)參數(shù)識別的時域方法和相平面法。Peng[17]提出利用一次近似頻率響應方程來識別弱非線性的單自由度振動系統(tǒng)參數(shù)的新方法。Yasuda[18]提出一種識別非線性多自由度系統(tǒng)的頻域方法。馬睿等[19]提出了一種柔性結構動力學模型修正方法，并將此方法運用于在地面模態(tài)試驗中由于重力而產(chǎn)生幾何非線性的太陽翼結構。

本文將描述函數(shù)法運用到含非線性鉸鏈的桁架結構的建模當中，采用諧波平衡法分析了含鉸結構的非線性動態(tài)特性，實現(xiàn)了空間含鉸結構動態(tài)建模及計算。在動響應分析基礎上，運用模式搜索法對可展結構鉸鏈的非線性剛度進行了模型修正的研究。

1 模型修正理論基礎

根據(jù)修正過程中使用實驗數(shù)據(jù)的不同，現(xiàn)有的模型修正方法可以大致分為基于模態(tài)參數(shù)的模型修正方法和基于頻響函數(shù)的模型修正方法兩大類，近年來也出現(xiàn)了基于時域相應的修正方法。但是對于非線性結構來說，已經(jīng)不存在線性系統(tǒng)中的模態(tài)概念，所以常見的是基于頻響函數(shù)的修正方法。基于頻響函數(shù)的修正計算的頻率范圍寬，采用適當數(shù)目頻率點上的頻響函數(shù)，便可求解問題，是結構動力學參數(shù)修正領域有發(fā)展前景的方法之一。

首先，定義結構位移響應的試驗測試值與諧波平衡法計算值的差值為殘差項Δ(P)

Δ(P)=HE(ω)-HA(ω,P)

(1)

式中：參數(shù)P代表需要識別的n個非線性參數(shù)向量，即P=[p1，p2，…，pn]；HE、HA分別代表響應的實驗值和計算值，根據(jù)最小二乘原則，若要計算所得的頻響函數(shù)能夠最佳擬合試驗結果

(2)

目標函數(shù)應最小，這便是基于頻響函數(shù)的參數(shù)識別方法的基本思路。試驗中，一般得不到幅頻曲線的解析表達式，而是離散的數(shù)據(jù)點，假設試驗選取的頻率點為ω1，ω2，…，ωn，代入式(2)可得：

(3)

則將修正問題轉(zhuǎn)化成為無約束最優(yōu)化問題。若能在參數(shù)P的合理取值范圍[P1，P2]內(nèi)找到一個值Pa，使得目標函數(shù)R(P)取極小值，則Pa為待修正參數(shù)的精確值。對于含鉸鏈的非線性系統(tǒng)，頻響函數(shù)通過數(shù)值方法求解獲得，故目標函數(shù)R(P)也是數(shù)值函數(shù)。對于桁架結構的模型參數(shù)修正，先進行非線性響應計算得到頻響函數(shù)，然后與實驗數(shù)據(jù)一起構造殘差函數(shù)，運用模式搜索法搜索殘差函數(shù)值最小時的參數(shù)值，即為修正后的模型參數(shù)。

2 非線性模型修正流程

對無約束最優(yōu)化問題來說，可以有多種直接搜索方法，模式搜索法是一種直接搜索優(yōu)化方法，其基本原理就是尋找一系列的點x0，x1，x2…，這些點都越來越靠近最優(yōu)值點，當搜索進行到終止條件時則將最后一個點作為本次搜索的解，一般不需要求解目標函數(shù)中的任何導數(shù)信息，僅對目標函數(shù)極值進行模式移動和探測移動搜索。在MATLAB中已經(jīng)有相關工具箱，調(diào)用pattern-search函數(shù)可以使用模式搜索法解決相關最優(yōu)化問題。利用模式搜索法的非線性結構模型修正方法流程圖見圖1，圖中FRF指頻響函數(shù)。

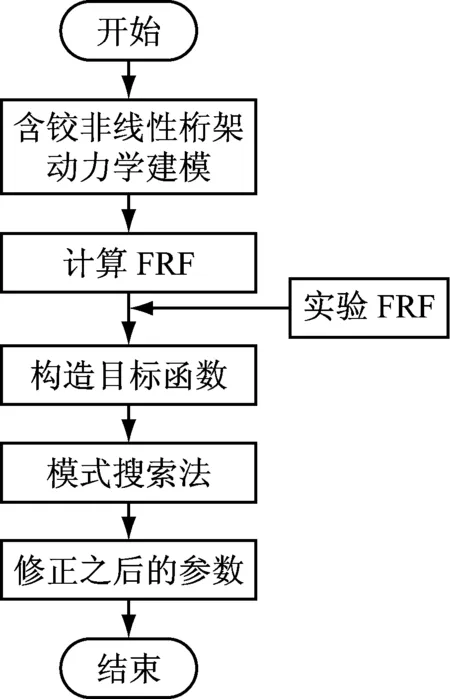
圖1 基于模式搜索法的修正流程

3 描述函數(shù)法與鉸鏈非線性特性

非線性系統(tǒng)的計算理論方法研究中，對于多自由度問題還有待進一步發(fā)展，目前比較常見的方法有：諧波平衡法、等效線性化法、直接積分法、相平面法、攝動法等等，這些方法有各自的特點和使用范圍，對于具體問題需要選擇合適的方法才能獲得理想的效果。含有鉸鏈的桁架結構屬于局部非線性系統(tǒng)，鉸鏈的非線性特性有固定的模型，采用諧波平衡法研究局部非線性系統(tǒng)在周期激勵下的穩(wěn)態(tài)響應，可以對系統(tǒng)的響應和鉸鏈的非線性恢復力進行諧波分解，從而將問題轉(zhuǎn)化為一組非線性代數(shù)方程組，采用數(shù)值方法求解，即可得到系統(tǒng)的非線性動力學響應。

對于弱非線性系統(tǒng)，可以利用諧波平衡法[20]分析受迫振動。設非線性系統(tǒng)受到頻率為ω的任意周期力F(t)的激勵，動力學方程為

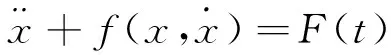
(4)

(5)

其中

(6)

代入動力學方程(4)，化為

(7)

(8)

將式(8)代入式(7)，利用三角函數(shù)公式將方程左邊化作各階諧波的線性組合，令左右兩邊各階諧波的系數(shù)相等，可推導出各階諧波的振幅an(n=1,2,…)與頻率ω之間的對應關系。當級數(shù)收斂時，諧波頻率愈高，振幅愈小。因此，實際計算時，可近似地取有限項代替無窮級數(shù)。對于非線性系統(tǒng)也可以做出與線性系統(tǒng)類似的頻譜圖，用于分析系統(tǒng)對周期激勵的響應狀況。

鉸鏈的非線性特性一般有間隙非線性、變剛度非線性、滯回非線性、立方非線性等幾種。本文考慮鉸鏈為立方非線性，鉸鏈恢復力具有奇函數(shù)特性，且有硬彈簧特性，力位移關系如圖2所示，非線性特性由一個參數(shù)來描述：接觸剛度系數(shù)kj。

含鉸結構和含單鉸懸臂梁的簡化模型分別如圖3和圖4所示，Kj為鉸鏈接觸剛度系數(shù)。

含鉸結構動力學方程為

(9)

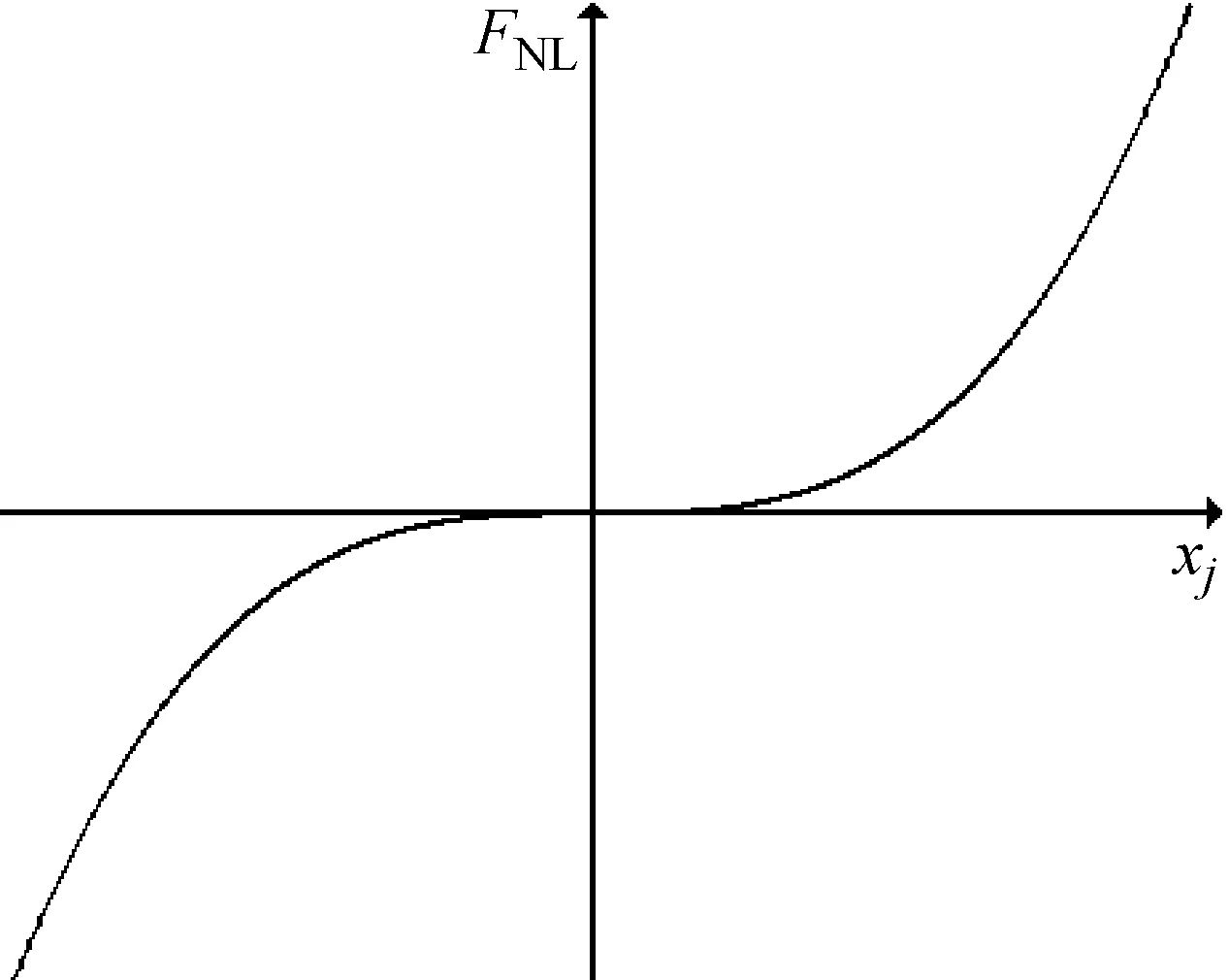
圖2 立方非線性力位移關系：FNL=Kj·x3

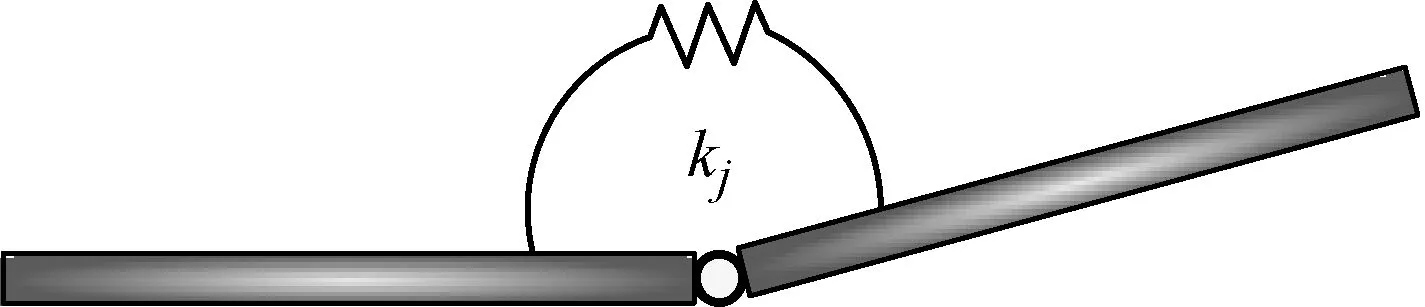
圖3 含鉸結構模型

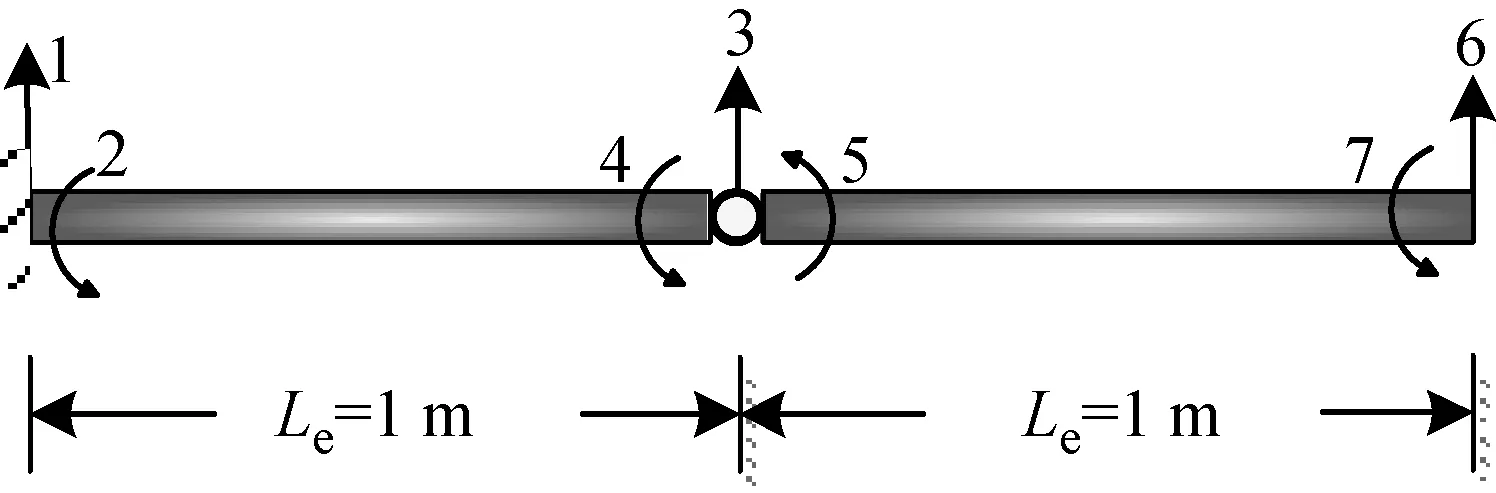
圖4 含單鉸懸臂梁

式中:M為質(zhì)量矩陣;X為節(jié)點位移向量;C為阻尼矩陣;C=αM+βK;K為剛度陣;FN為鉸鏈引入的非線性廣義力向量;FE為外部激振廣義力向量。

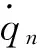
(10)

式中:an和bn為廣義位移qn諧波展開中的正余弦系數(shù)。

鉸鏈引入的非線性力可以用廣義位移和速度表示為

(11)

式中：

(12)

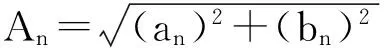
4 算例研究

4.1 含鉸懸臂梁

4.1.1 頻響函數(shù)計算

以圖4所示的一維含鉸懸臂梁為研究對象，運用1.2中的基本理論對該結構進行建模與分析計算，梁的基本參數(shù)見表1。

考慮正弦激勵作用在自由端，設激振力幅值和剛度初始分別為F=0.5EI/L2，Kj=0.1EI/Le，圖4中結構的頻響函數(shù)變化情況如圖5和圖6所示。由圖可知，隨著激勵幅值和鉸鏈接觸剛度系數(shù)的增加，結構的固有頻率增大。

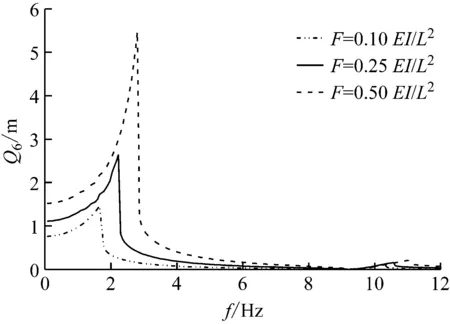
圖5 激勵幅值變化對頻響函數(shù)的影響

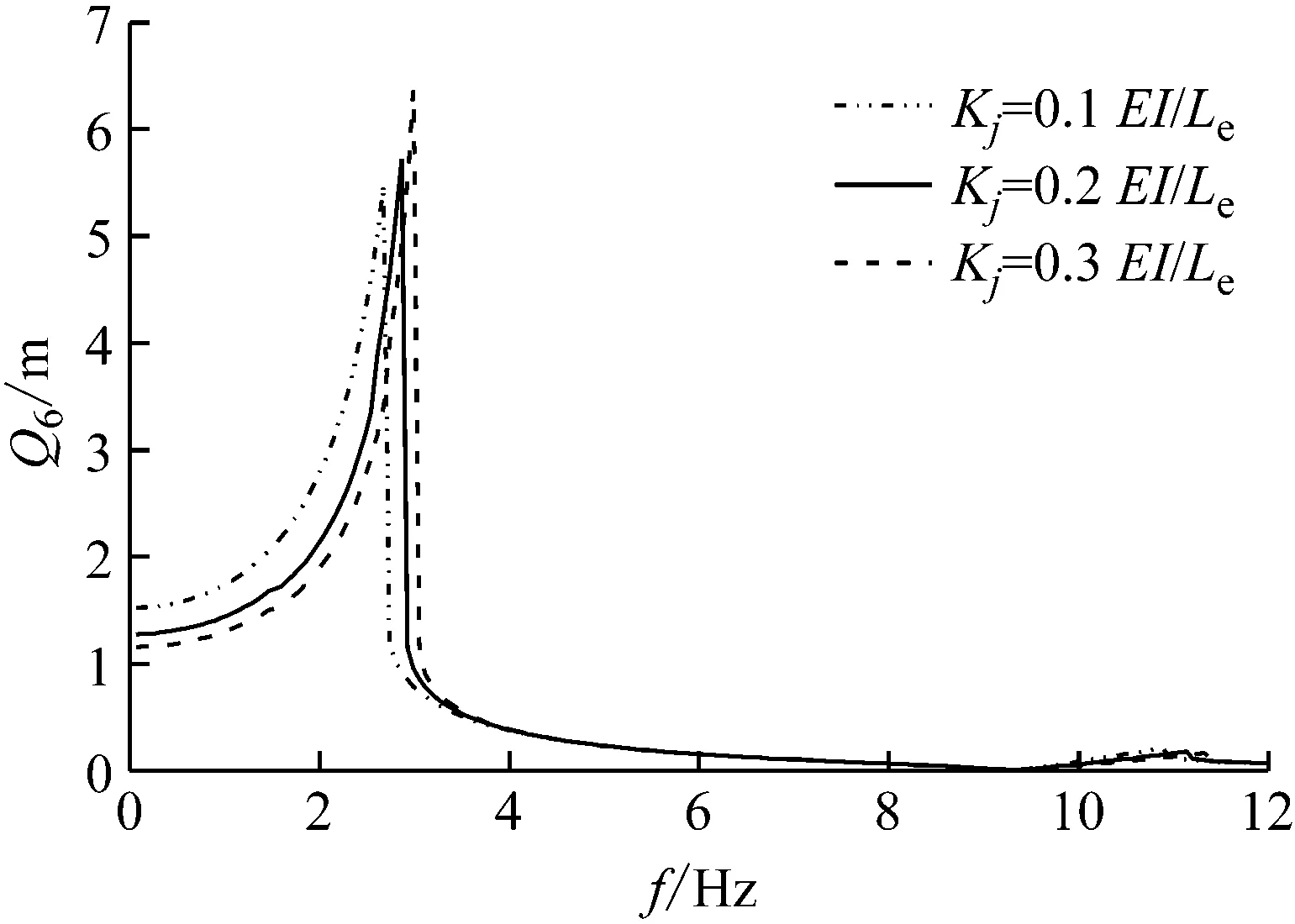
圖6 鉸鏈接觸剛度系數(shù)變化對頻響函數(shù)的影響

4.1.2 非線性剛度修正

設激振力幅值仍為F=0.5EI/L2，以鉸鏈接觸剛度系數(shù)Kj=0.1EI/Le作為實驗值，假設模型中剛度Kj存在15%的初始誤差，為0.115EI/Le。以圖4中自由度6的非線性頻響為特征量構造目標函數(shù)，利用模式搜索法對含鉸懸臂梁結構進行模型修正，修正后值為0.1EI/Le，與實驗值相吻合。圖7為試驗頻響、初始模型頻響和修正后模型頻響比較結果，可見修正后的鉸鏈接觸剛度系數(shù)沒有誤差。

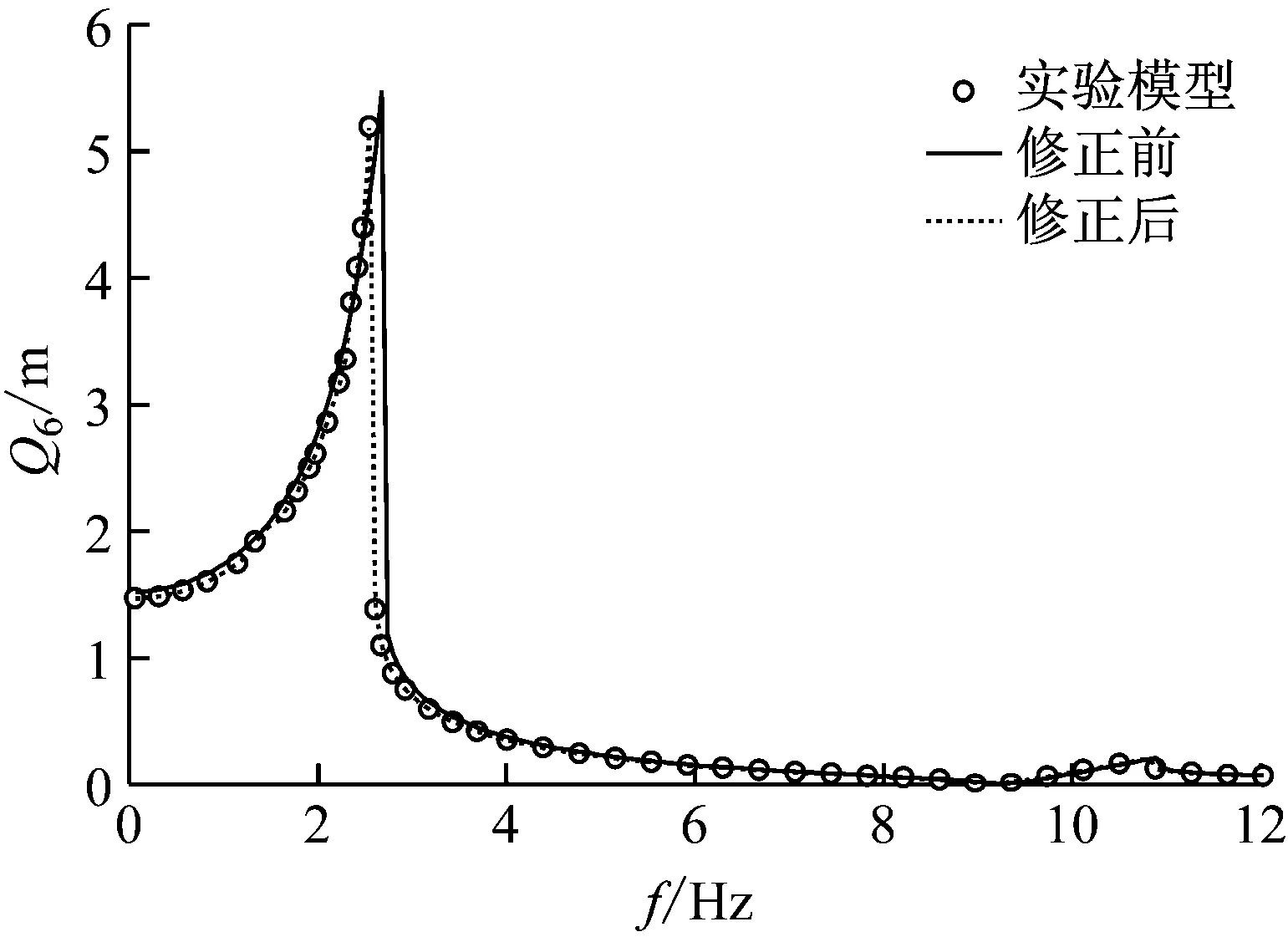
圖7 15%初始參數(shù)誤差修正后頻響函數(shù)比較

4.2 平面桁架

4.2.1 頻響函數(shù)計算

單跨平面桁架結構示意圖和動力學模型，如圖8和9所示。

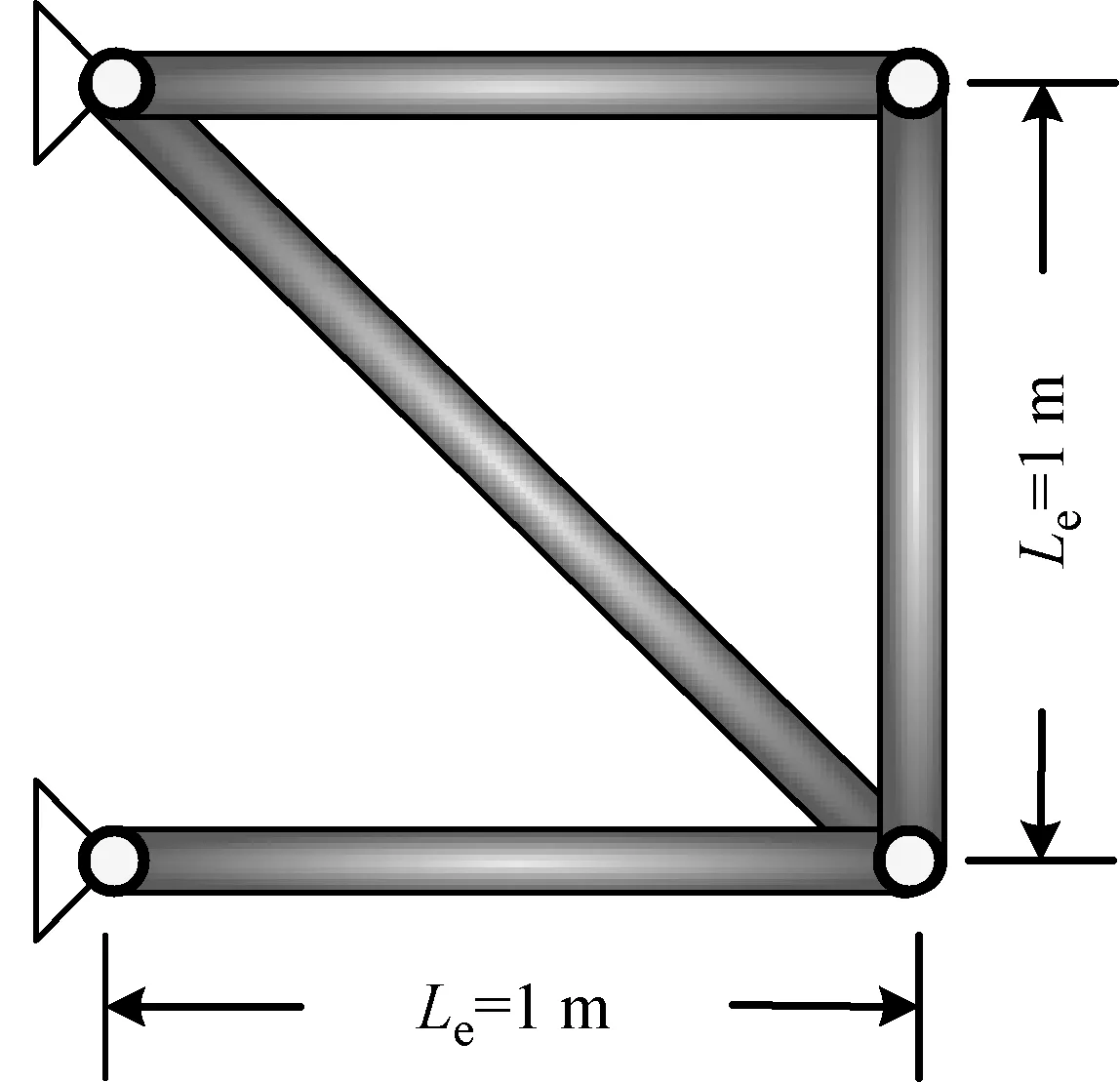
圖8 單跨平面桁架結構示意圖

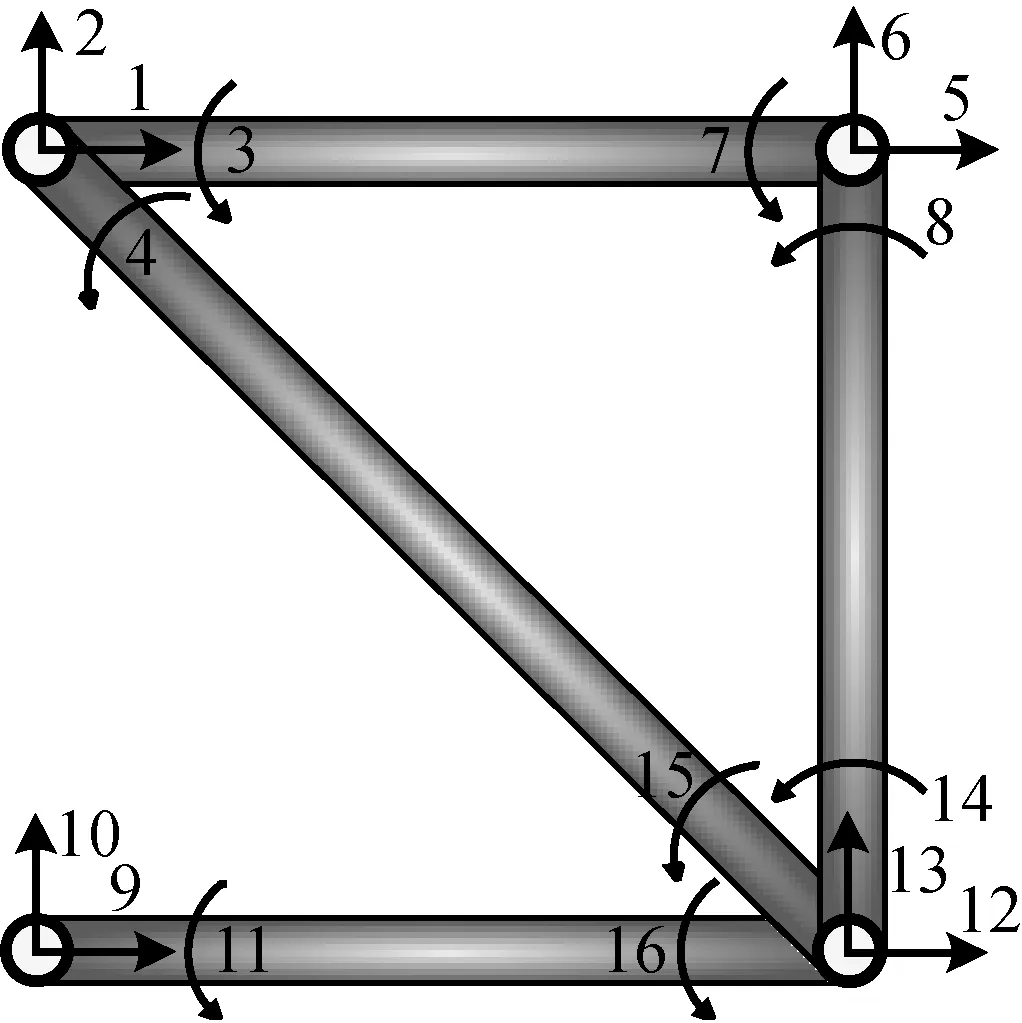
圖9 單跨平面桁架動力學模型

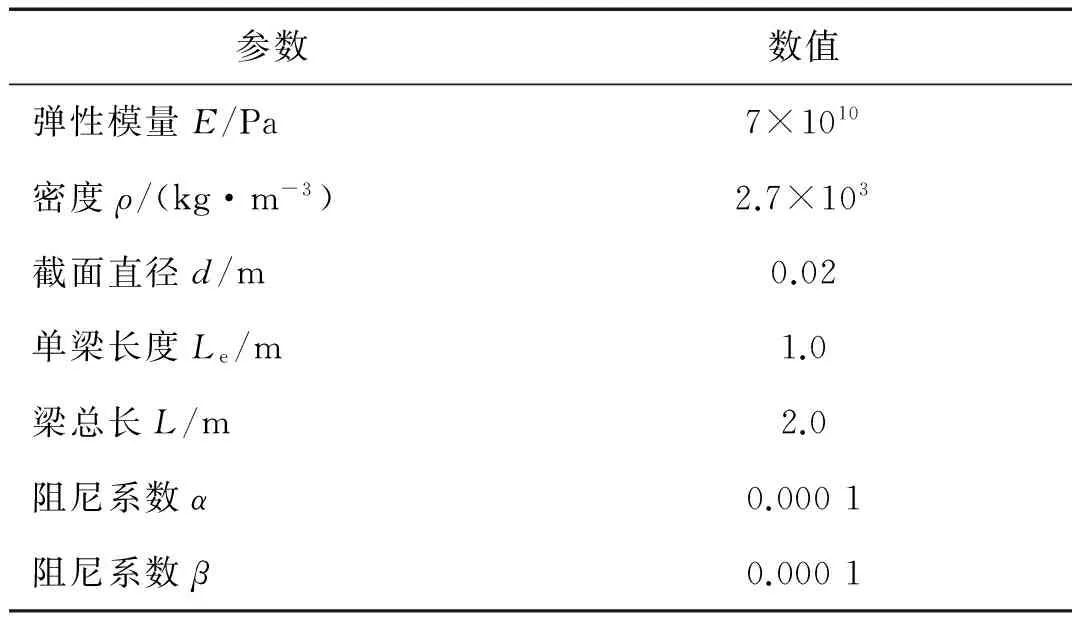
表1 梁結構的參數(shù)表

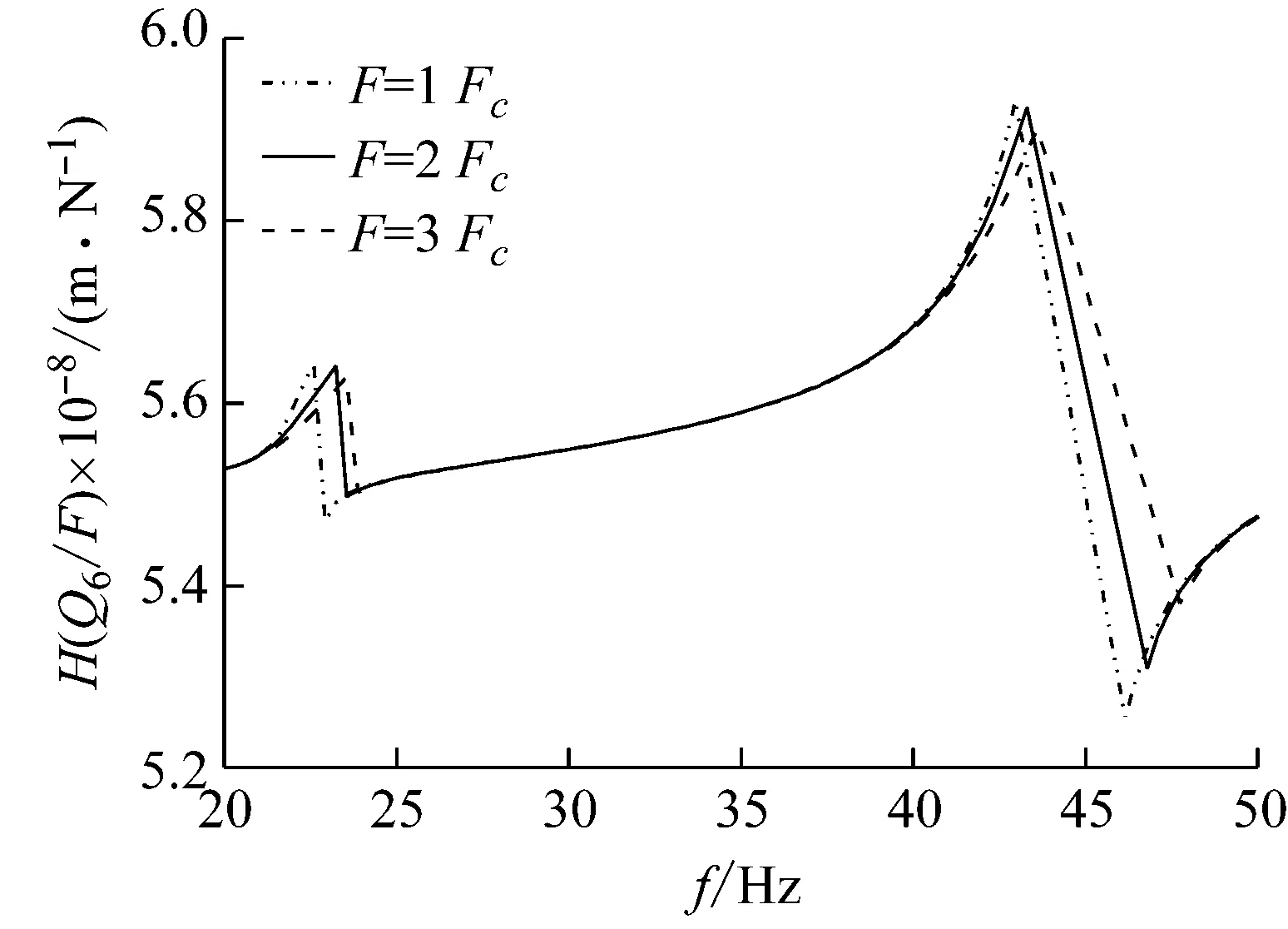
圖10 激勵幅值變化對頻響函數(shù)影響

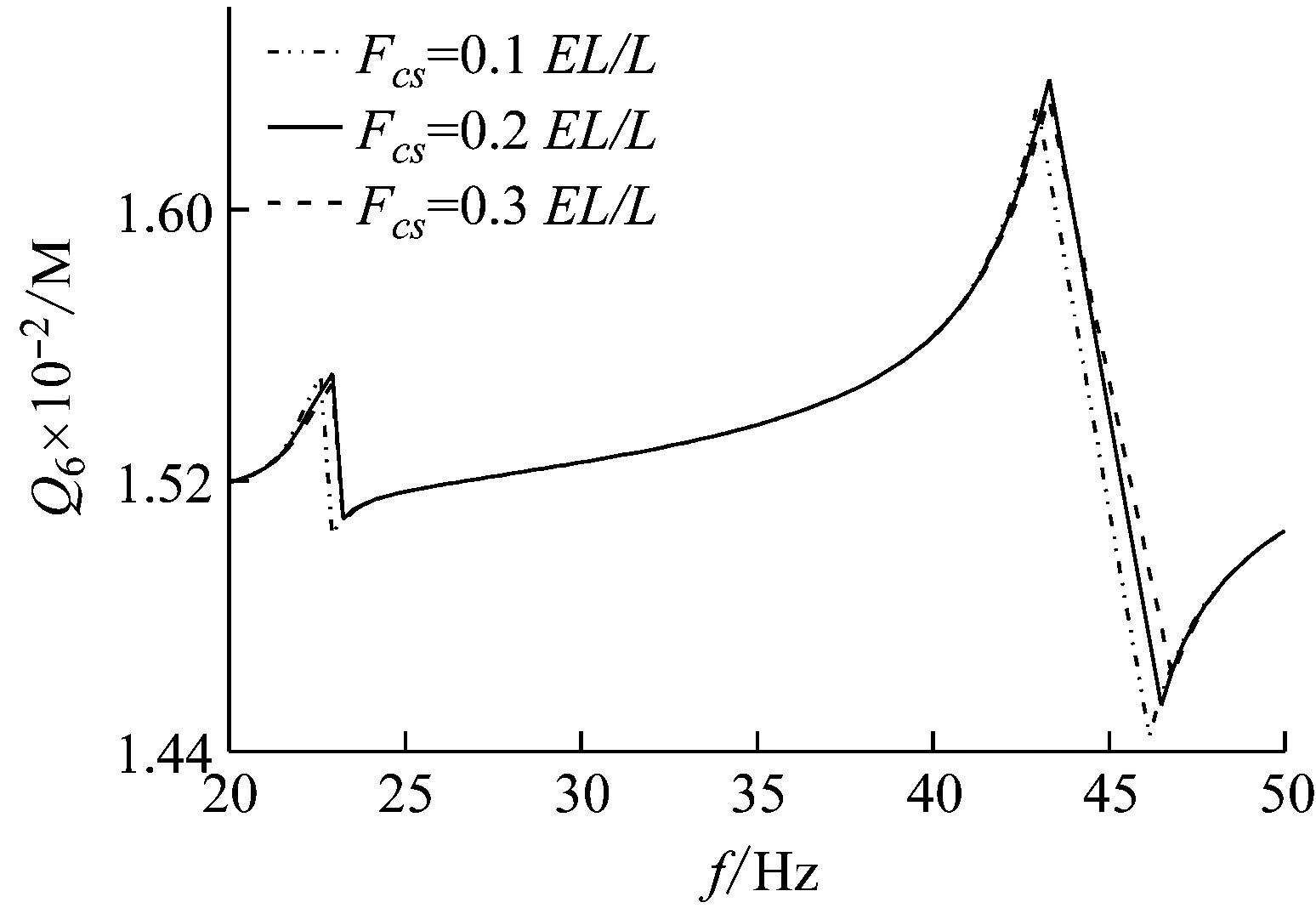
圖11 鉸鏈接觸剛度系數(shù)變化對頻響函數(shù)影響

4.2.2 非線性剛度修正

設激振力幅值仍為F=Fc，以鉸鏈接觸剛度系數(shù)Kj=0.1EI/Le作為實驗值，假設模型中剛度Kj存在50%的較大初始誤差，為0.15EI/Le。利用模式搜索法對含鉸平面桁架結構進行模型修正，修正后值為0.1EI/Le，與實驗值相吻合。圖12為試驗頻響、初始模型頻響和修正后模型頻響比較，可見修正后的鉸鏈接觸剛度系數(shù)沒有誤差。

然而在真實實驗過程中，將不可避免地存在各種噪聲的干擾，為了模擬真實的實驗環(huán)境并且為了檢驗本文提出方法的抗噪能力，對實驗測得的頻響函數(shù)添加不同的隨機白噪聲,令H(ω)=H(ω)(1+snr·μ)，SNR(Signal Noise Ratio)為信噪比，μ為-1～1的隨機數(shù)[21]。利用模式搜索法進行修正，修正后值與誤差如表2所示，說明該修正方法的具有一定的抗噪能力。

表2 不同噪聲時修正誤差對比

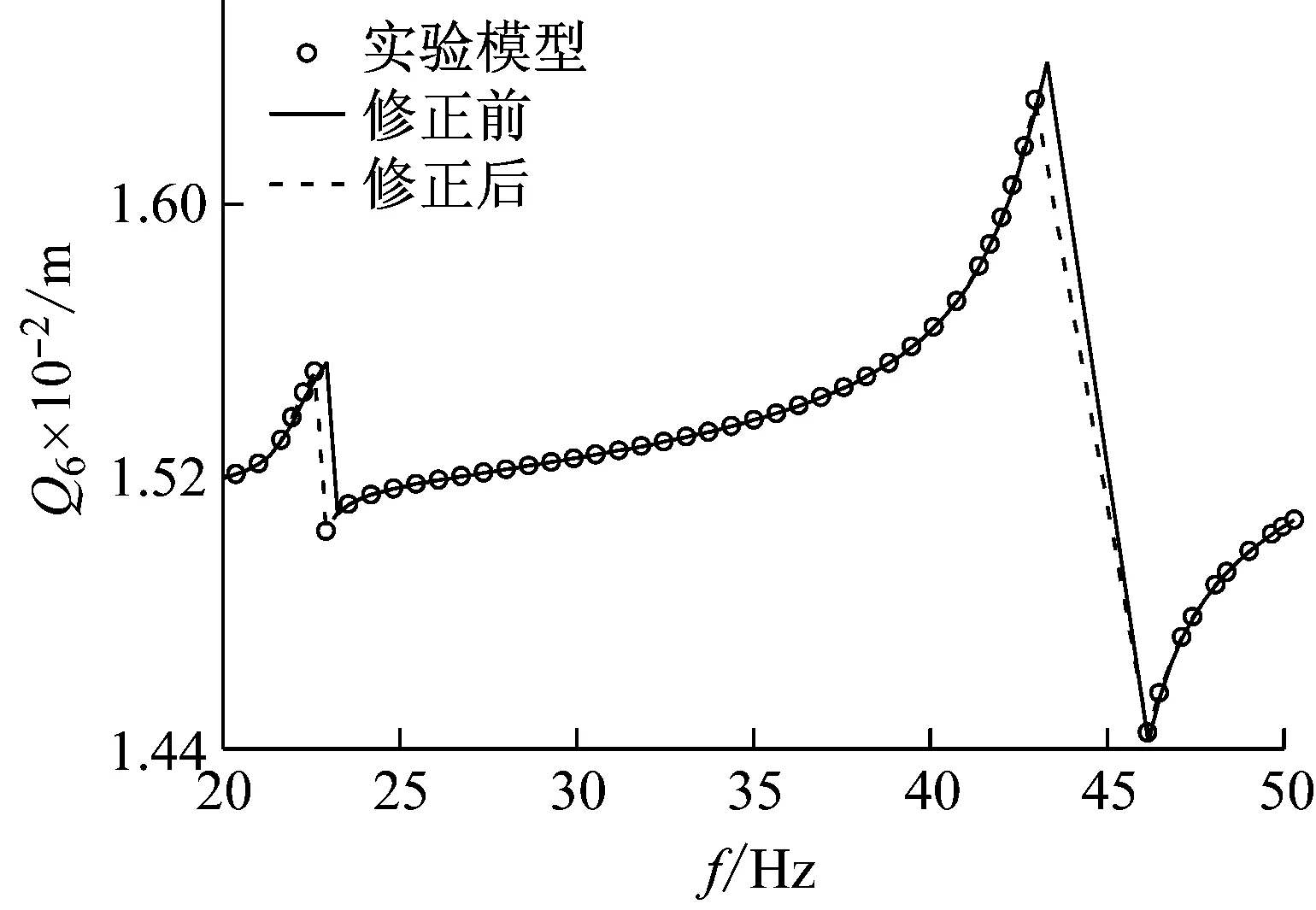
圖12 50%初始參數(shù)誤差修正后頻響函數(shù)比較

一般地，桁架中的鉸鏈接觸剛度系數(shù)不完全相同，假設模型中的上面和下面兩個鉸鏈的剛度兩兩相同，分別為Kj1，Kj2，以考察該修正方法對多參數(shù)修正的精度。設激振力幅值仍為F=Fc，以鉸鏈接觸剛度系數(shù)Kj1=0.1EI/Le，Kj2=0.2EI/Le作為實驗值，假設模型中剛度Kj1和Kj2分別存在存在+50%和-50%的較大初始誤差，為0.15EI/Le和0.1EI/Le。利用模式搜索法進行模型修正，修正后值為0.1019EI/Le和0.1993EI/Le，誤差為1.9%和0.7%，可見該方法對多參數(shù)修正的精度較高，圖13為試驗頻響、初始模型頻響和修正后模型頻響函數(shù)的比較。

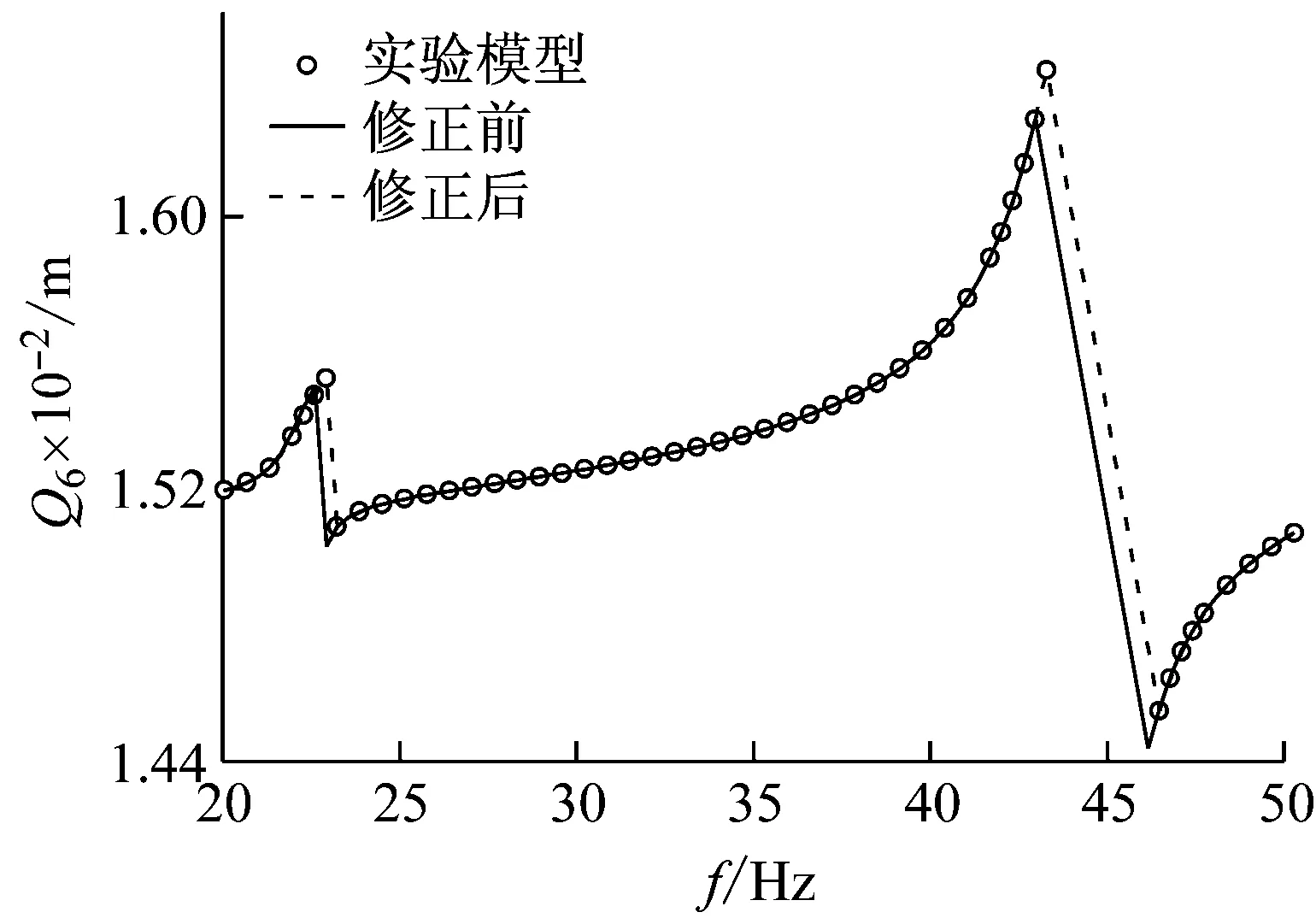
圖13 多參數(shù)±50%初始誤差修正后頻響函數(shù)比較

5 結 論

本文提出了利用非線性頻響函數(shù)對含鉸非線性桁架結構進行模型參數(shù)修正的方法。

(1) 利用諧波平衡法對含鉸結構進行了非線性動力學建模與響應計算，包括一維含鉸梁和二維含鉸平面桁架，假設鉸鏈的非線性特性為立方非線性模型，得到了結構頻響函數(shù)隨著激勵幅值和鉸鏈接觸剛度系數(shù)的變化規(guī)律，即固有頻率分別隨著激勵幅值和鉸鏈接觸剛度系數(shù)的增大而增大。

(2) 采用模式搜索法對鉸鏈的剛度進行修正，頻響曲線比較結果顯示，在步長和收斂準則合理的情況下，修正后結構參數(shù)誤差最可達到0。鉸梁結構中剛度初始假設誤差較小為15%，桁架結構中剛度初始假設誤差較大為50%，說明該方法是對非線性結構進行模型修正的有效方法，同時具有較高的精確性。

(3) 針對實際測試環(huán)境和結構，分別考慮試驗信號加入不同的噪聲和不同鉸鏈接觸剛度系數(shù)參數(shù)。該方法對引入2%噪聲后的修正誤差僅為2.2%，說明具有一定的抗噪聲干擾能力；將鉸鏈接觸剛度系數(shù)參數(shù)調(diào)整為兩個時，該方法的修正誤差較小，表明方法同樣適用于多參數(shù)模型修正。

[1] BROWN M A. A deployable mast for solar sails in the range of 100-1000m [J]. Advances in Space Research, 2011, 48(11):1747-1753.

[2] 趙林燕. 星載可展開天線展開過程的仿真與分析[D]. 西安: 西安電子科技大學, 2011:1- 6.

[3] 郭宏偉, 劉榮強, 鄧宗全. 空間索桿鉸接式伸展臂性能參數(shù)分析與設計[J]. 北京航空航天大學學報, 2008, 24(10):1186-1190.

GUO Hongwei, LIU Rongqiang, DENG Zongquan. Per-formance of parameters analysis and design of space cable-strut deployable articulated mast[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 24(10): 1186-1190.

[4] FERNEY B D, FOLKMAN S L. Results of force-state mapping tests to characterize struts using pinned joints[C]∥Proceedings of the 36th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Con-ference. 1995.

[5] FOLKMANT S L, BINGHAM J G, CROOKSTON J R. The joint damping experiment[R]. NASA,1997.

[6] TOMIHIKO Y. Dynamic characteristic formulations for jointed space structures[J]. Journal of Spacecraft and Rockets, 2006, 43(4):771-779.

[7] BOWDEN M L. Dynamics of space structures with nonlinear joints[D]. Cambridge: Massachusetts Institute of Tech-nology, 1988.

[8] WEBSTER M S. Modeling beam-like space trusses with nonlinear joints with application to control[D]. Cambridge: Massachusetts Institute of Technology. 1991.

[9] SARKAR S, VENKATRAMAN K. Dynamics of flexible structures with nonlinear joints[J]. Journal of Vibration and Acoustics, 2004, 126(1):92-100.

[10] 黃鐵球, 吳德隆, 閻紹澤. 帶間隙伸展機構的非線性動力學建模[J]. 中國空間科學技術, 1999, 19(1):7-13.

HUANG Tieqiu, WU Delong, YAN Shaoze. Nonlinear dynamic modeling of deployable structures with clearance[J]. Chinese Space Science and Technology, 1999, 19(1): 7-13.

[11] 陳鹿民, 閻紹澤，金德聞，等. 含間隙鉸空間可展桁架結構的動力學實驗研究[J].清華大學學報, 2003, 43(8): 1027-1030.

CHEN Lumin, YAN Shaoze, JIN Dewen, et al. Dynamics experiment of a space deployable truss structure with joint clearance[J]. Journal of Tsinghua University, 2003, 43(8): 1027-1030.

[12] 尉立肖, 劉才山. 圓柱鉸間隙運動學分析及動力學仿真[J]. 北京大學學報, 2005, 41(5): 679-687.

WEI Lixiao, LIU Caishan. Kinematic analysis and dynamics simulation of cylinder joint clearance[J]. Journal of Peking University, 2005, 41(5): 679-687.

[13] 閻紹澤, 葉青, 申永勝, 等. 間隙對空間可展結構動力學性能的影響[J]. 導彈與航天運載技術, 2002(6): 42-46.

YAN Shaoze, YE Qing, SHEN Yongsheng, et al. Effects of clearances on dynamic performances of deployable structures for spacecraft[J]. Missiles and Space Vehicles, 2002(6): 42-46.

[14] JIANG Dong，ZHANG Peng，F(xiàn)EI Qingguo，et al. Comparative study of model updating methods using frequency response function data[J]. Journal of Vibroengineering, 2014, 16(5): 2305-2318.

[15] 費慶國, 李愛群, 張令彌. 基于神經(jīng)網(wǎng)絡的非線性結構有限元模型修正研究[J]. 宇航學報, 2005, 26(3):267-269.

FEI Qingguo, LI Aiqun, ZHANG Lingmi. Research on updating of finite element model of nonlinear structures based on neural network[J]. Journal of Astronautics, 2005, 26(3):267-269.

[16] TANG Jiashi, HUO Quangzhong. Identifying parameters of nonlinear system in time domain by the response of free vibration[J]. Journal of Vibration Engineering,1989,2:1-6.

[17] PENG Jiehua. Frequency method of parameter identification of nonlinear systems[J]. Journal of Shaoyang University,2004(3):3-10.

[18] YASUDA K. Identification of nonlinear multi-degree-of-freedom systems[J]. JSME International Journal,1988,31(1):1-8.

[19] 馬睿, 姜東, 費慶國, 等. 考慮重力影響的太陽翼模型修正方法研究[J]. 宇航學報, 2014, 35(12): 1373-1378.

MA Rui, JIANG Dong, FEI Qingguo, et al. A model updating method for solar array considering the influence of gravity[J]. Journal of Astronautics, 2014, 35(12): 1373-1378.

[20] 劉延柱,陳立群,陳文良.振動力學[M]. 北京: 高等教育出版社, 2011.

[21] 李偉明, 洪嘉振. 基于頻響函數(shù)的模型修正方法[J]. 上海交通大學學報, 2011, 45(10): 1455-1459.

LI Weiming, HONG Jiazhen. Research on model updating method based on frequency response functions[J]. Journal of Shanghai Jiaotong University, 2011, 45(10): 1455-1459.